7.3 平行线的性质 课件(共21张PPT)
文档属性
| 名称 | 7.3 平行线的性质 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 06:04:36 | ||
图片预览





文档简介
第七章 相交线与平行线
3 平行线的性质
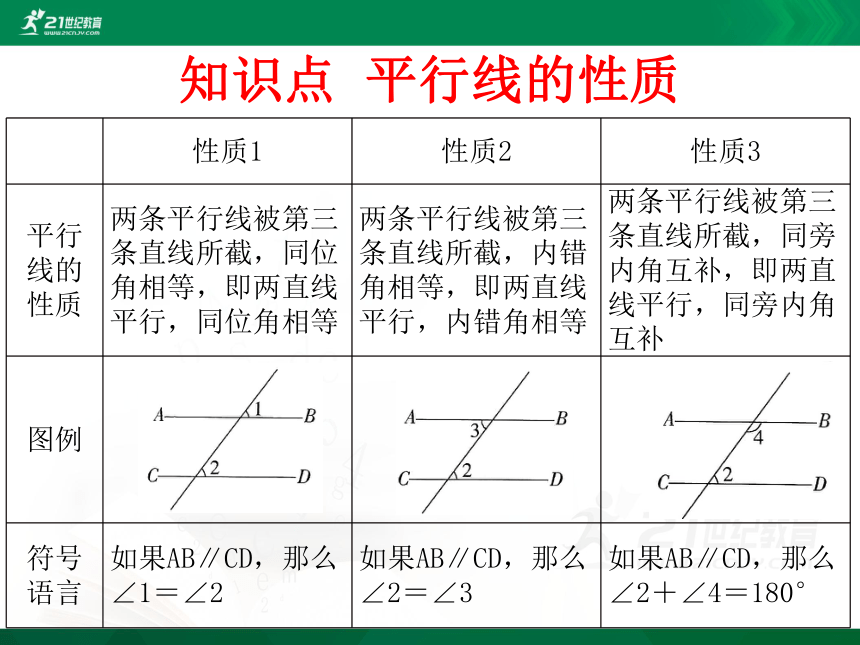
知识点 平行线的性质
性质1
性质2
性质3
平行线的性质
图例
符号语言
知识点 平行线的性质
性质1
性质2
性质3
平行线的性质
两条平行线被第三条直线所截,同位角相等,即两直线平行,同位角相等
两条平行线被第三条直线所截,内错角相等,即两直线平行,内错角相等
两条平行线被第三条直线所截,同旁内角互补,即两直线平行,同旁内角互补
图例
符号语言
如果AB∥CD,那么∠1=∠2
如果AB∥CD,那么∠2=∠3
如果AB∥CD,那么∠2+∠4=180°
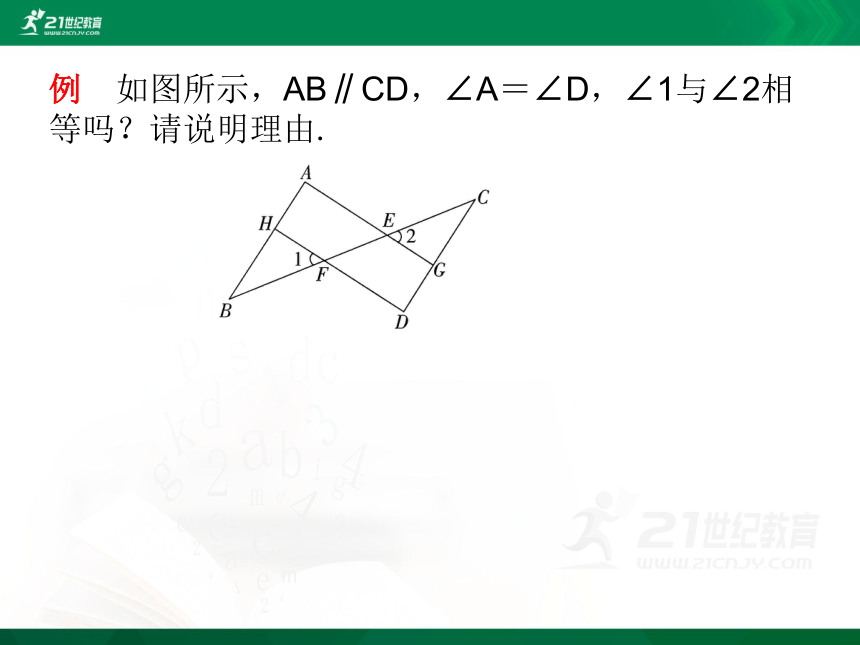
例 如图所示,AB∥CD,∠A=∠D,∠1与∠2相等吗?请说明理由.
例 如图所示,AB∥CD,∠A=∠D,∠1与∠2相等吗?请说明理由.
解析 ∠1=∠2理由:
因为AB∥CD,所以∠A=∠CGE,
又因为∠A=∠D,所以∠D=∠CGE,
所以AG∥HD,所以∠1=∠AEF,
又因为∠2=∠AEF,所以∠1=∠2.
经典例题
题型一 利用平行线的性质进行与角有关的计算
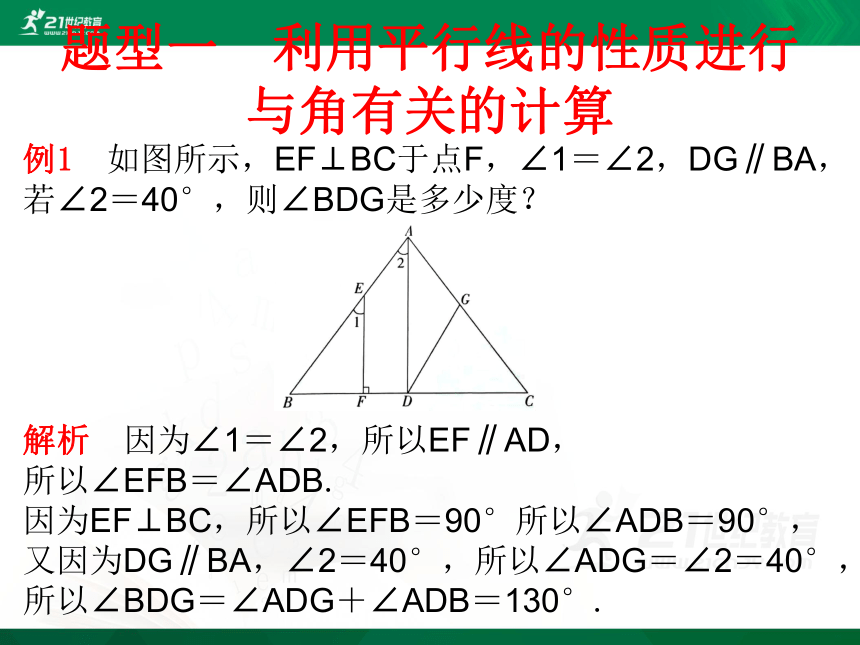
例1 如图所示,EF⊥BC于点F,∠1=∠2,DG∥BA,若∠2=40°,则∠BDG是多少度?
题型一 利用平行线的性质进行与角有关的计算
例1 如图所示,EF⊥BC于点F,∠1=∠2,DG∥BA,若∠2=40°,则∠BDG是多少度?
解析 因为∠1=∠2,所以EF∥AD,
所以∠EFB=∠ADB.
因为EF⊥BC,所以∠EFB=90°所以∠ADB=90°,
又因为DG∥BA,∠2=40°,所以∠ADG=∠2=40°,
所以∠BDG=∠ADG+∠ADB=130°.
题型二 平行线性质与判定的综合运用
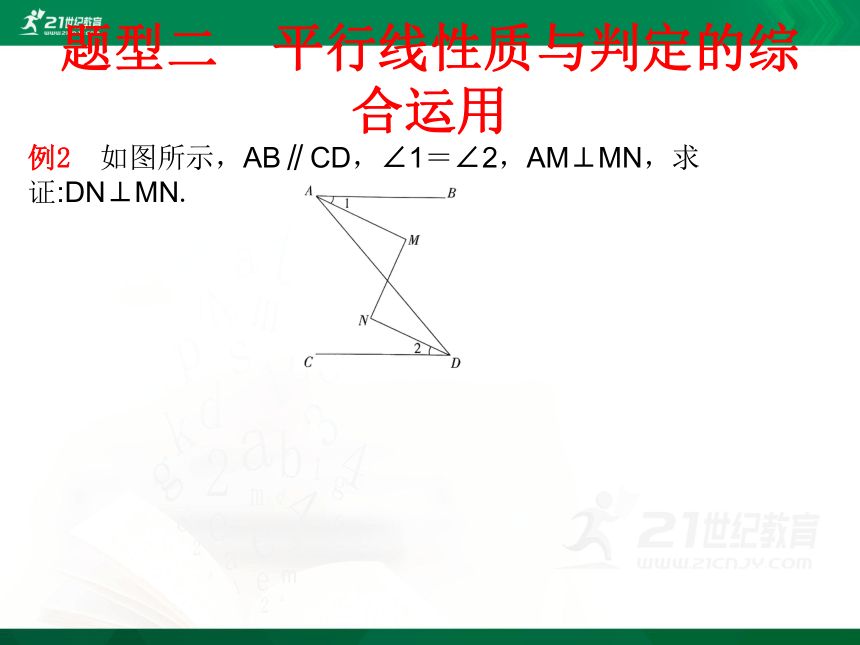
例2 如图所示,AB∥CD,∠1=∠2,AM⊥MN,求证:DN⊥MN.
题型二 平行线性质与判定的综合运用
例2 如图所示,AB∥CD,∠1=∠2,AM⊥MN,求证:DN⊥MN.
证明 ∵AB∥CD,∴∠BAD=∠ADC,
∵∠1=∠2,∴∠BAD-∠1=∠ADC-∠2,即∠MAD=∠ADN,
∴AM∥DN,∴∠M=∠N,
∵A⊥MN,∴∠M=90°,∴∠N=∠M=90°,∴DN⊥MN.
题型二 平行线性质与判定的综合运用
例2 如图所示,AB∥CD,∠1=∠2,AM⊥MN,求证:DN⊥MN.
证明 ∵AB∥CD,∴∠BAD=∠ADC,
∵∠1=∠2,∴∠BAD-∠1=∠ADC-∠2,即∠MAD=∠ADN,
∴AM∥DN,∴∠M=∠N,
∵A⊥MN,∴∠M=90°,∴∠N=∠M=90°,∴DN⊥MN.
点拔 本题思路:平行→内错角相等→平行→内错角相等,综合运用了平行线的性质与判定.
题型三 直尺或三角板中的平行线
例3 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.60° B.65° C.75° D.85°
题型三 直尺或三角板中的平行线
例3 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.60° B.65° C.75° D.85°
解析 如图所示,
因为∠BCA=60°,∠DCE=45°,∠BCA+∠DCE+∠2=180°,所以∠2=180°-60°-45°=75°.
因为HF∥BC,所以∠1=∠2=75°.
题型三 直尺或三角板中的平行线
例3 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.60° B.65° C.75° D.85°
解析 如图所示,
因为∠BCA=60°,∠DCE=45°,∠BCA+∠DCE+∠2=180°,所以∠2=180°-60°-45°=75°.
因为HF∥BC,所以∠1=∠2=75°.
答案 C
题型四 平行线的性质在方向角中的应用
例4 如图所示,水面上的某舰艇在A处看C岛位于北偏东60°方向,当它到达B处时看C岛位于北偏西45°方向,则∠ACB的度数是( )
A.75° B.90° C.100° D.105°
题型四 平行线的性质在方向角中的应用
例4 如图所示,水面上的某舰艇在A处看C岛位于北偏东60°方向,当它到达B处时看C岛位于北偏西45°方向,则∠ACB的度数是( )
A.75° B.90° C.100° D.105°
解析 如图所示,过点C作CE∥AN,则∠3=∠1=60°.
易知AN∥BD,所以CE∥BD,所以∠4=∠2=45°.
所以∠ACB=∠3+∠4=60°+45°=105°.
题型四 平行线的性质在方向角中的应用
例4 如图所示,水面上的某舰艇在A处看C岛位于北偏东60°方向,当它到达B处时看C岛位于北偏西45°方向,则∠ACB的度数是( )
A.75° B.90° C.100° D.105°
解析 如图所示,过点C作CE∥AN,则∠3=∠1=60°.
易知AN∥BD,所以CE∥BD,所以∠4=∠2=45°.
所以∠ACB=∠3+∠4=60°+45°=105°.
答案 D
易错易混
易错点 看到两直线被第三条直线所截,默认两直线平行
例 下列说法正确的有
①两直线被第三条直线所截,同位角相等;
②两直线被第三条直线所截,同旁内角互补;
③两直线平行,同旁内角相等;
④两直线平行,内错角相等
A.4个 B.3个 C.2个 D.1个
易错点 看到两直线被第三条直线所截,默认两直线平行
例 下列说法正确的有
①两直线被第三条直线所截,同位角相等;
②两直线被第三条直线所截,同旁内角互补;
③两直线平行,同旁内角相等;
④两直线平行,内错角相等
A.4个 B.3个 C.2个 D.1个
错解 B 正解 D
易错点 看到两直线被第三条直线所截,默认两直线平行
例 下列说法正确的有
①两直线被第三条直线所截,同位角相等;
②两直线被第三条直线所截,同旁内角互补;
③两直线平行,同旁内角相等;
④两直线平行,内错角相等
A.4个 B.3个 C.2个 D.1个
错解 B 正解 D
错因分析 两直线被第三条直线所截,两直线不一定平行.
3 平行线的性质
知识点 平行线的性质
性质1
性质2
性质3
平行线的性质
图例
符号语言
知识点 平行线的性质
性质1
性质2
性质3
平行线的性质
两条平行线被第三条直线所截,同位角相等,即两直线平行,同位角相等
两条平行线被第三条直线所截,内错角相等,即两直线平行,内错角相等
两条平行线被第三条直线所截,同旁内角互补,即两直线平行,同旁内角互补
图例
符号语言
如果AB∥CD,那么∠1=∠2
如果AB∥CD,那么∠2=∠3
如果AB∥CD,那么∠2+∠4=180°
例 如图所示,AB∥CD,∠A=∠D,∠1与∠2相等吗?请说明理由.
例 如图所示,AB∥CD,∠A=∠D,∠1与∠2相等吗?请说明理由.
解析 ∠1=∠2理由:
因为AB∥CD,所以∠A=∠CGE,
又因为∠A=∠D,所以∠D=∠CGE,
所以AG∥HD,所以∠1=∠AEF,
又因为∠2=∠AEF,所以∠1=∠2.
经典例题
题型一 利用平行线的性质进行与角有关的计算
例1 如图所示,EF⊥BC于点F,∠1=∠2,DG∥BA,若∠2=40°,则∠BDG是多少度?
题型一 利用平行线的性质进行与角有关的计算
例1 如图所示,EF⊥BC于点F,∠1=∠2,DG∥BA,若∠2=40°,则∠BDG是多少度?
解析 因为∠1=∠2,所以EF∥AD,
所以∠EFB=∠ADB.
因为EF⊥BC,所以∠EFB=90°所以∠ADB=90°,
又因为DG∥BA,∠2=40°,所以∠ADG=∠2=40°,
所以∠BDG=∠ADG+∠ADB=130°.
题型二 平行线性质与判定的综合运用
例2 如图所示,AB∥CD,∠1=∠2,AM⊥MN,求证:DN⊥MN.
题型二 平行线性质与判定的综合运用
例2 如图所示,AB∥CD,∠1=∠2,AM⊥MN,求证:DN⊥MN.
证明 ∵AB∥CD,∴∠BAD=∠ADC,
∵∠1=∠2,∴∠BAD-∠1=∠ADC-∠2,即∠MAD=∠ADN,
∴AM∥DN,∴∠M=∠N,
∵A⊥MN,∴∠M=90°,∴∠N=∠M=90°,∴DN⊥MN.
题型二 平行线性质与判定的综合运用
例2 如图所示,AB∥CD,∠1=∠2,AM⊥MN,求证:DN⊥MN.
证明 ∵AB∥CD,∴∠BAD=∠ADC,
∵∠1=∠2,∴∠BAD-∠1=∠ADC-∠2,即∠MAD=∠ADN,
∴AM∥DN,∴∠M=∠N,
∵A⊥MN,∴∠M=90°,∴∠N=∠M=90°,∴DN⊥MN.
点拔 本题思路:平行→内错角相等→平行→内错角相等,综合运用了平行线的性质与判定.
题型三 直尺或三角板中的平行线
例3 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.60° B.65° C.75° D.85°
题型三 直尺或三角板中的平行线
例3 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.60° B.65° C.75° D.85°
解析 如图所示,
因为∠BCA=60°,∠DCE=45°,∠BCA+∠DCE+∠2=180°,所以∠2=180°-60°-45°=75°.
因为HF∥BC,所以∠1=∠2=75°.
题型三 直尺或三角板中的平行线
例3 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.60° B.65° C.75° D.85°
解析 如图所示,
因为∠BCA=60°,∠DCE=45°,∠BCA+∠DCE+∠2=180°,所以∠2=180°-60°-45°=75°.
因为HF∥BC,所以∠1=∠2=75°.
答案 C
题型四 平行线的性质在方向角中的应用
例4 如图所示,水面上的某舰艇在A处看C岛位于北偏东60°方向,当它到达B处时看C岛位于北偏西45°方向,则∠ACB的度数是( )
A.75° B.90° C.100° D.105°
题型四 平行线的性质在方向角中的应用
例4 如图所示,水面上的某舰艇在A处看C岛位于北偏东60°方向,当它到达B处时看C岛位于北偏西45°方向,则∠ACB的度数是( )
A.75° B.90° C.100° D.105°
解析 如图所示,过点C作CE∥AN,则∠3=∠1=60°.
易知AN∥BD,所以CE∥BD,所以∠4=∠2=45°.
所以∠ACB=∠3+∠4=60°+45°=105°.
题型四 平行线的性质在方向角中的应用
例4 如图所示,水面上的某舰艇在A处看C岛位于北偏东60°方向,当它到达B处时看C岛位于北偏西45°方向,则∠ACB的度数是( )
A.75° B.90° C.100° D.105°
解析 如图所示,过点C作CE∥AN,则∠3=∠1=60°.
易知AN∥BD,所以CE∥BD,所以∠4=∠2=45°.
所以∠ACB=∠3+∠4=60°+45°=105°.
答案 D
易错易混
易错点 看到两直线被第三条直线所截,默认两直线平行
例 下列说法正确的有
①两直线被第三条直线所截,同位角相等;
②两直线被第三条直线所截,同旁内角互补;
③两直线平行,同旁内角相等;
④两直线平行,内错角相等
A.4个 B.3个 C.2个 D.1个
易错点 看到两直线被第三条直线所截,默认两直线平行
例 下列说法正确的有
①两直线被第三条直线所截,同位角相等;
②两直线被第三条直线所截,同旁内角互补;
③两直线平行,同旁内角相等;
④两直线平行,内错角相等
A.4个 B.3个 C.2个 D.1个
错解 B 正解 D
易错点 看到两直线被第三条直线所截,默认两直线平行
例 下列说法正确的有
①两直线被第三条直线所截,同位角相等;
②两直线被第三条直线所截,同旁内角互补;
③两直线平行,同旁内角相等;
④两直线平行,内错角相等
A.4个 B.3个 C.2个 D.1个
错解 B 正解 D
错因分析 两直线被第三条直线所截,两直线不一定平行.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
