3.1 平面直角坐标系同步练习(含解析)
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册3.1平面直角坐标系
同步练习
一、单选题
1.根据下列表述,能确定位置的是
A.?天益广场南区?????????????B.?凤凰山北偏东
?????????????C.?红旗影院5排9座?????????????D.?学校操场的西面
2.已知点P到x轴的距离为1,到y轴的距离为2,则点P的坐标不可能为( )
A.?(1,2)?????????????????????????B.?(-2,-1)?????????????????????????C.?(2,-1)?????????????????????????D.?(2,1)
3.下列说法错误的是(???
)
A.?在x轴上的点的坐标纵坐标都是0,横坐标为任意数??????????????????B.?坐标原点的横、纵坐标都是0
C.?在y轴上的点的坐标的特点是横坐标都是0,纵坐标都大于0?????D.?坐标轴上的点不属于任何象限
4.点(﹣2,3)在平面直角坐标系中所在的象限是(?
?)
A.?第一象限???????????????????????????B.?第二象限???????????????????????????C.?第三象限???????????????????????????D.?第四象限
5.点P在四象限,且点P到x轴的距离为3,点P到y轴的距离为2,则点P的坐标为(???
)
A.?(-3,-2)?????????????????????????B.?(3,-2)?????????????????????????C.?(2,3)?????????????????????????D.?(2,-3)
6.下列说法错误的是(???
)
A.?在x轴上的点的纵坐标为0???????????????????????????????????????????????????B.?点P(﹣1,3)到y轴的距离是1
C.?若xy
0,x﹣y
0,那么点Q(x
,
y)在第四象限?????D.?点A(﹣a2﹣1,|b|)一定在第二象限
7.如图,是雷达探测器测得的结果,图中显示在点A,B,C,D,E,F处有目标出现,目标的表示方法为(r,α),其中,r表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.例如,点A,D的位置表示为A(5,30°),D(4,240°).用这种方法表示点B,C,E,F的位置,其中正确的是(??
)
A.?B(2,90°)?????????????????B.?C(2,120°)?????????????????C.?E(3,120°)?????????????????D.?F(4,210°)
8.如图,已知棋子“车”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为(
??)
A.?(2,2)????????????????????????????????B.?(-2,2)????????????????????????????????C.?(3,2)????????????????????????????????D.?(3,1)
9.若点P(3a+5,-6a-2)在第四象限,且到两坐标轴的距离相等,则a的值为(??
)
A.?-1?????????????????????????????????????????B.??????????????????????????????????????????C.?1?????????????????????????????????????????D.?2
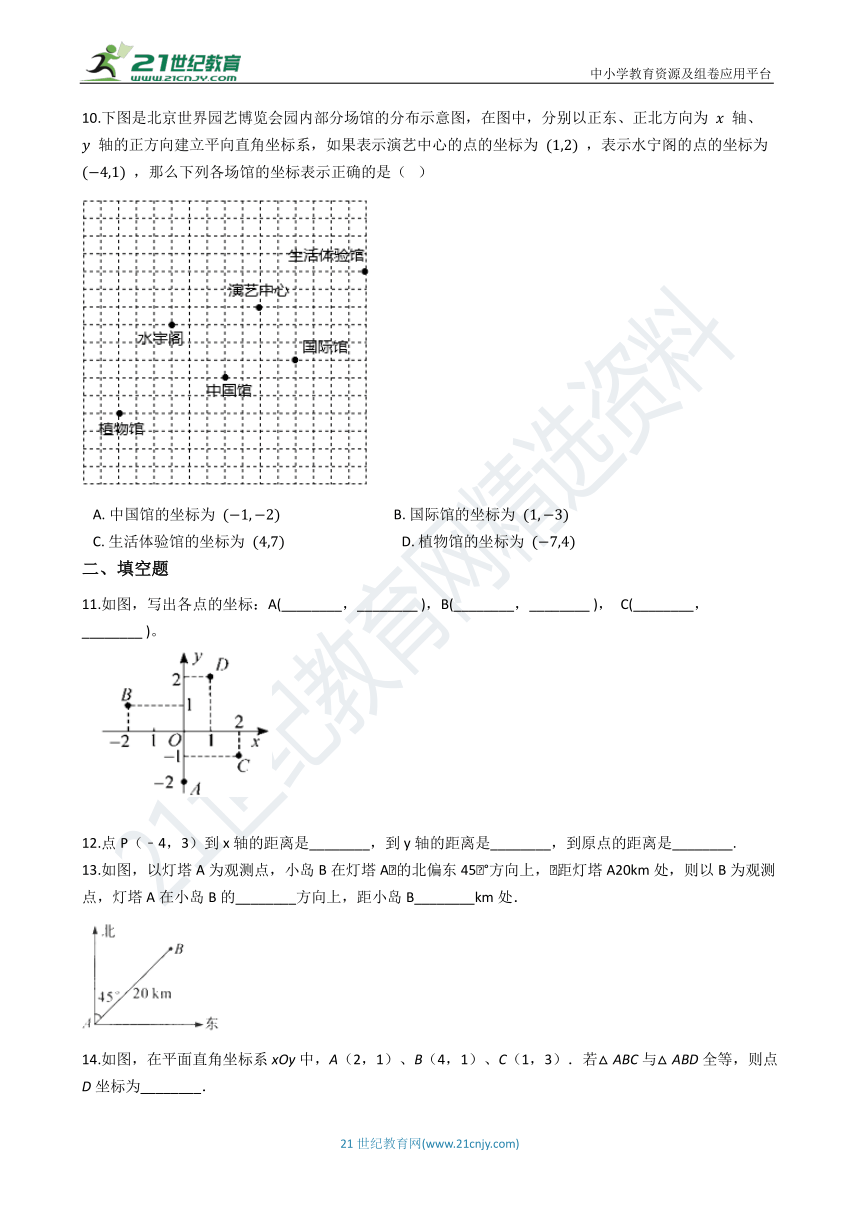
10.下图是北京世界园艺博览会园内部分场馆的分布示意图,在图中,分别以正东、正北方向为
轴、
轴的正方向建立平向直角坐标系,如果表示演艺中心的点的坐标为
,表示水宁阁的点的坐标为
,那么下列各场馆的坐标表示正确的是(?
)
A.?中国馆的坐标为
?????????????????????????????????B.?国际馆的坐标为
C.?生活体验馆的坐标为
??????????????????????????????????D.?植物馆的坐标为
二、填空题
11.如图,写出各点的坐标:A(________,________?),B(________,________?),
C(________,________?)。
12.点P(﹣4,3)到x轴的距离是________,到y轴的距离是________,到原点的距离是________.
13.如图,以灯塔A为观测点,小岛B在灯塔A的北偏东45°方向上,距灯塔A20km处,则以B为观测点,灯塔A在小岛B的________方向上,距小岛B________km处.
14.如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).若△ABC与△ABD全等,则点D坐标为________.
三、解答题
15.如图是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(-2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置.
四、作图题
16.在一次夏令营活动中,主办方告诉营员们A、B两点的位置及坐标分别为(-3,1)、(-2,-3),同时只告诉营员们活动中心C的坐标为(3,2)(单位:km)
(1)请在图中建立直角坐标系并确定点C的位置;
(2)若营员们打算从点B处直接赶往C处,请用方向角B和距离描述点C相对于点B的位置.
五、综合题
17.小明给右图建立平面直角坐标系,使医院的坐标为(0,0),火车站的坐标为(2,2).
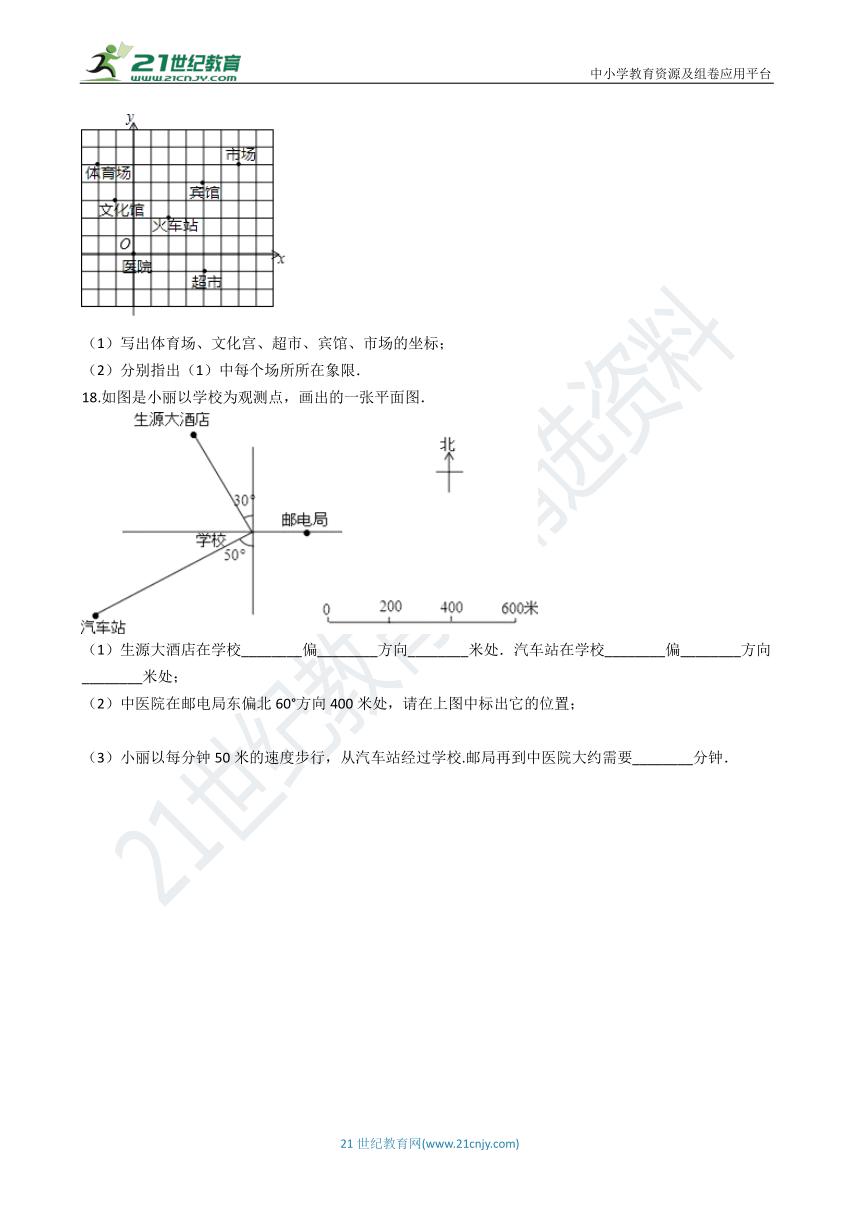
(1)写出体育场、文化宫、超市、宾馆、市场的坐标;
(2)分别指出(1)中每个场所所在象限.
18.如图是小丽以学校为观测点,画出的一张平面图.
(1)生源大酒店在学校________偏________方向________米处.汽车站在学校________偏________方向________米处;
(2)中医院在邮电局东偏北60°方向400米处,请在上图中标出它的位置;
(3)小丽以每分钟50米的速度步行,从汽车站经过学校.邮局再到中医院大约需要________分钟.
答案解析部分
一、单选题
1.【答案】
C
解:A、天益广场南区,不能确定位置,故本选项不符合题意;
B、凤凰山北偏东
,没有明确具体位置,故本选项不符合题意;
C、红旗影院5排9座,能确定位置,故本选项符合题意;
D、学校操场的西面,不能确定位置,故本选项不符合题意;
故答案为:C.
2.【答案】
A
解:∵点P到x轴的距离为1,到y轴的距离为2,
∴点P的横坐标为2或-2,纵坐标为1或-1,
∴点P的坐标不可能为(1,2).
故答案为:A.
【分析】根据点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度求出点P可能的横坐标与纵坐标,即可得解.
3.【答案】
C
解:A、在x轴上的点的坐标纵坐标都是0,横坐标为任意数,说法正确,不符合题意;
B、坐标原点的横、纵坐标都是0,说法正确,不符合题意;
C、在y轴上的点的坐标的特点是横坐标都是0,纵坐标为任意数,原说法错误,符合题意;
D、坐标轴上的点不属于任何象限,说法正确,不符合题意.
故答案为:C.
4.【答案】
B
解:点(﹣2,3)所在的象限是第二象限,
故答案为:B.
5.【答案】
D
解:根据平面直角坐标系的特点,可知P点的横坐标为+2,纵坐标为-3,
因此P点的坐标为(+2,-3).
故答案为:D.
6.【答案】
D
解:A.在x轴上的点的纵坐标为0,故本选项不合题意;
B.点P(﹣1,3)到y轴的距离是1,故本选项不合题意;
C.若xy<0,x﹣y>0,则x>0,y<0,所以点Q(x,y)在第四象限,故本选项不合题意;
D.﹣a2﹣1<0,|b|≥0,所以点A(﹣a2﹣1,|b|)在x轴或第二象限,故本选项符合题意.
故答案为:D.
7.【答案】
A
解:A、由题意可得:B(2,90°),故符合题意;
B、由题意可得:C(3,120°),故不符合题意;
C、由题意可得:E(3,300°),故不符合题意;
D、由题意可得:F(5,210°),故不符合题意;
故答案为:A.
8.【答案】
C
解:∵“车”的坐标为(-2,3),“马”的坐标为(1,3),
∴建立平面直角坐标系如图,
∴“炮”的坐标为(3,2).
故答案为:C.
9.【答案】
C
解:∵点P(3a+5,-6a-2)在第四象限,且到两坐标轴的距离相等,
∴3a+5+(-6a-2)=0,
解得a=1,
此时,3a+5=8,-6a-2=-8,符合.
故答案为:C.
10.【答案】
A
解:根据题意可建立如下所示平面直角坐标系,
A、中国馆的坐标为(-1,-2),故本选项符合题意;
B、国际馆的坐标为(3,-1),故本选项不符合题意;
C、生活体验馆的坐标为(7,4),故本选项不符合题意;
D、植物馆的坐标为(-7,-4),故本选项不符合题意.
故答案为:A.
二、填空题
11.【答案】
0;-2;-2;1;2;-1
解:依题可得:
A(0,-2),B(-2,1),C(2,-1),D(1,2).
故答案为:0;-2;-2;1;2;-1;1;2.
12.【答案】
3;4;5
解:
点P坐标为(-4,3),
点P到
x轴的距离是:
|3|=3;
到y轴的距离:
|-4|=4,
到原点的距离为:
=5.
故答案为:
3,4,5.
13.【答案】
南偏西45°;20
解:以B为观测点,在B点建立方位图,那么灯塔A在小岛B的南偏西45°方向上,距小岛B
20km处.
故答案为:南偏西45°,20.
14.【答案】
(1,﹣1),(5,3)或(5,﹣1).
解:首先画出平面直角坐标系,然后根据三角形全等的性质进行求解.
三、解答题
15.【答案】
解:建立如图所示的平面直角坐标系:
小广场(0,0)、雷达(4,0)、营房(2,-3)、码头(-1,-2)
四、作图题
16.【答案】
(1)解:根据A(-3,1),B(-2,-3)画出直角坐标系,
描出点C(3,2),如图所示:
(2)解:∵BC=5
,
∴点C在点B北偏东45°方向上,距离点B的5
km处.
五、综合题
17.【答案】
(1)解:(1)体育场的坐标为(﹣2,5),文化宫的坐标为(﹣1,3),超市的坐标为(4,﹣1),宾馆的坐标为(4,4),市场的坐标为(6,5)
(2)解:体育场、文化宫在第二象限,市场、宾馆在第一象限,超市在第四象限
18.【答案】
(1)解:北;西30°;400;南;西50°;600
(2)解:因为400米=40000厘米,
则中医院到邮电局的图上距离是:40000×
=2(厘米);
如图所示,即为中医院的位置:
(3)24
解:(1)生源大酒店在学校在学校北偏西30°处,汽车站在学校南偏西50°方向,
量得学校到生源大酒店的距离是2厘米,
则学校到生源大酒店的实际距离是:2÷
=40000(厘米)=400(米);
量得学校到汽车站的距离是3厘米,
则学校到汽车站的实际距离是:3÷
=60000(厘米)=600(米);
故答案为:北.西30°.400.南.西50°.600;
(
3
)量得学校到邮电局的图上距离为1厘米,
则学校到邮电局的实际距离为:1÷
=20000(厘米)=200(米);
所以小丽需要的时间为:
(600+200+400)÷50=1200÷50=24(分钟)
答:小丽以每分钟50米的速度步行,从汽车站经过学校.邮局再到中医院大约需要24分钟.
故答案为:24.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册3.1平面直角坐标系
同步练习
一、单选题
1.根据下列表述,能确定位置的是
A.?天益广场南区?????????????B.?凤凰山北偏东
?????????????C.?红旗影院5排9座?????????????D.?学校操场的西面
2.已知点P到x轴的距离为1,到y轴的距离为2,则点P的坐标不可能为( )
A.?(1,2)?????????????????????????B.?(-2,-1)?????????????????????????C.?(2,-1)?????????????????????????D.?(2,1)
3.下列说法错误的是(???
)
A.?在x轴上的点的坐标纵坐标都是0,横坐标为任意数??????????????????B.?坐标原点的横、纵坐标都是0
C.?在y轴上的点的坐标的特点是横坐标都是0,纵坐标都大于0?????D.?坐标轴上的点不属于任何象限
4.点(﹣2,3)在平面直角坐标系中所在的象限是(?
?)
A.?第一象限???????????????????????????B.?第二象限???????????????????????????C.?第三象限???????????????????????????D.?第四象限
5.点P在四象限,且点P到x轴的距离为3,点P到y轴的距离为2,则点P的坐标为(???
)
A.?(-3,-2)?????????????????????????B.?(3,-2)?????????????????????????C.?(2,3)?????????????????????????D.?(2,-3)
6.下列说法错误的是(???
)
A.?在x轴上的点的纵坐标为0???????????????????????????????????????????????????B.?点P(﹣1,3)到y轴的距离是1
C.?若xy
0,x﹣y
0,那么点Q(x
,
y)在第四象限?????D.?点A(﹣a2﹣1,|b|)一定在第二象限
7.如图,是雷达探测器测得的结果,图中显示在点A,B,C,D,E,F处有目标出现,目标的表示方法为(r,α),其中,r表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.例如,点A,D的位置表示为A(5,30°),D(4,240°).用这种方法表示点B,C,E,F的位置,其中正确的是(??
)
A.?B(2,90°)?????????????????B.?C(2,120°)?????????????????C.?E(3,120°)?????????????????D.?F(4,210°)
8.如图,已知棋子“车”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为(
??)
A.?(2,2)????????????????????????????????B.?(-2,2)????????????????????????????????C.?(3,2)????????????????????????????????D.?(3,1)
9.若点P(3a+5,-6a-2)在第四象限,且到两坐标轴的距离相等,则a的值为(??
)
A.?-1?????????????????????????????????????????B.??????????????????????????????????????????C.?1?????????????????????????????????????????D.?2
10.下图是北京世界园艺博览会园内部分场馆的分布示意图,在图中,分别以正东、正北方向为
轴、
轴的正方向建立平向直角坐标系,如果表示演艺中心的点的坐标为
,表示水宁阁的点的坐标为
,那么下列各场馆的坐标表示正确的是(?
)
A.?中国馆的坐标为
?????????????????????????????????B.?国际馆的坐标为
C.?生活体验馆的坐标为
??????????????????????????????????D.?植物馆的坐标为
二、填空题
11.如图,写出各点的坐标:A(________,________?),B(________,________?),
C(________,________?)。
12.点P(﹣4,3)到x轴的距离是________,到y轴的距离是________,到原点的距离是________.
13.如图,以灯塔A为观测点,小岛B在灯塔A的北偏东45°方向上,距灯塔A20km处,则以B为观测点,灯塔A在小岛B的________方向上,距小岛B________km处.
14.如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).若△ABC与△ABD全等,则点D坐标为________.
三、解答题
15.如图是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(-2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置.
四、作图题
16.在一次夏令营活动中,主办方告诉营员们A、B两点的位置及坐标分别为(-3,1)、(-2,-3),同时只告诉营员们活动中心C的坐标为(3,2)(单位:km)
(1)请在图中建立直角坐标系并确定点C的位置;
(2)若营员们打算从点B处直接赶往C处,请用方向角B和距离描述点C相对于点B的位置.
五、综合题
17.小明给右图建立平面直角坐标系,使医院的坐标为(0,0),火车站的坐标为(2,2).
(1)写出体育场、文化宫、超市、宾馆、市场的坐标;
(2)分别指出(1)中每个场所所在象限.
18.如图是小丽以学校为观测点,画出的一张平面图.
(1)生源大酒店在学校________偏________方向________米处.汽车站在学校________偏________方向________米处;
(2)中医院在邮电局东偏北60°方向400米处,请在上图中标出它的位置;
(3)小丽以每分钟50米的速度步行,从汽车站经过学校.邮局再到中医院大约需要________分钟.
答案解析部分
一、单选题
1.【答案】
C
解:A、天益广场南区,不能确定位置,故本选项不符合题意;
B、凤凰山北偏东
,没有明确具体位置,故本选项不符合题意;
C、红旗影院5排9座,能确定位置,故本选项符合题意;
D、学校操场的西面,不能确定位置,故本选项不符合题意;
故答案为:C.
2.【答案】
A
解:∵点P到x轴的距离为1,到y轴的距离为2,
∴点P的横坐标为2或-2,纵坐标为1或-1,
∴点P的坐标不可能为(1,2).
故答案为:A.
【分析】根据点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度求出点P可能的横坐标与纵坐标,即可得解.
3.【答案】
C
解:A、在x轴上的点的坐标纵坐标都是0,横坐标为任意数,说法正确,不符合题意;
B、坐标原点的横、纵坐标都是0,说法正确,不符合题意;
C、在y轴上的点的坐标的特点是横坐标都是0,纵坐标为任意数,原说法错误,符合题意;
D、坐标轴上的点不属于任何象限,说法正确,不符合题意.
故答案为:C.
4.【答案】
B
解:点(﹣2,3)所在的象限是第二象限,
故答案为:B.
5.【答案】
D
解:根据平面直角坐标系的特点,可知P点的横坐标为+2,纵坐标为-3,
因此P点的坐标为(+2,-3).
故答案为:D.
6.【答案】
D
解:A.在x轴上的点的纵坐标为0,故本选项不合题意;
B.点P(﹣1,3)到y轴的距离是1,故本选项不合题意;
C.若xy<0,x﹣y>0,则x>0,y<0,所以点Q(x,y)在第四象限,故本选项不合题意;
D.﹣a2﹣1<0,|b|≥0,所以点A(﹣a2﹣1,|b|)在x轴或第二象限,故本选项符合题意.
故答案为:D.
7.【答案】
A
解:A、由题意可得:B(2,90°),故符合题意;
B、由题意可得:C(3,120°),故不符合题意;
C、由题意可得:E(3,300°),故不符合题意;
D、由题意可得:F(5,210°),故不符合题意;
故答案为:A.
8.【答案】
C
解:∵“车”的坐标为(-2,3),“马”的坐标为(1,3),
∴建立平面直角坐标系如图,
∴“炮”的坐标为(3,2).
故答案为:C.
9.【答案】
C
解:∵点P(3a+5,-6a-2)在第四象限,且到两坐标轴的距离相等,
∴3a+5+(-6a-2)=0,
解得a=1,
此时,3a+5=8,-6a-2=-8,符合.
故答案为:C.
10.【答案】
A
解:根据题意可建立如下所示平面直角坐标系,
A、中国馆的坐标为(-1,-2),故本选项符合题意;
B、国际馆的坐标为(3,-1),故本选项不符合题意;
C、生活体验馆的坐标为(7,4),故本选项不符合题意;
D、植物馆的坐标为(-7,-4),故本选项不符合题意.
故答案为:A.
二、填空题
11.【答案】
0;-2;-2;1;2;-1
解:依题可得:
A(0,-2),B(-2,1),C(2,-1),D(1,2).
故答案为:0;-2;-2;1;2;-1;1;2.
12.【答案】
3;4;5
解:
点P坐标为(-4,3),
点P到
x轴的距离是:
|3|=3;
到y轴的距离:
|-4|=4,
到原点的距离为:
=5.
故答案为:
3,4,5.
13.【答案】
南偏西45°;20
解:以B为观测点,在B点建立方位图,那么灯塔A在小岛B的南偏西45°方向上,距小岛B
20km处.
故答案为:南偏西45°,20.
14.【答案】
(1,﹣1),(5,3)或(5,﹣1).
解:首先画出平面直角坐标系,然后根据三角形全等的性质进行求解.
三、解答题
15.【答案】
解:建立如图所示的平面直角坐标系:
小广场(0,0)、雷达(4,0)、营房(2,-3)、码头(-1,-2)
四、作图题
16.【答案】
(1)解:根据A(-3,1),B(-2,-3)画出直角坐标系,
描出点C(3,2),如图所示:
(2)解:∵BC=5
,
∴点C在点B北偏东45°方向上,距离点B的5
km处.
五、综合题
17.【答案】
(1)解:(1)体育场的坐标为(﹣2,5),文化宫的坐标为(﹣1,3),超市的坐标为(4,﹣1),宾馆的坐标为(4,4),市场的坐标为(6,5)
(2)解:体育场、文化宫在第二象限,市场、宾馆在第一象限,超市在第四象限
18.【答案】
(1)解:北;西30°;400;南;西50°;600
(2)解:因为400米=40000厘米,
则中医院到邮电局的图上距离是:40000×
=2(厘米);
如图所示,即为中医院的位置:
(3)24
解:(1)生源大酒店在学校在学校北偏西30°处,汽车站在学校南偏西50°方向,
量得学校到生源大酒店的距离是2厘米,
则学校到生源大酒店的实际距离是:2÷
=40000(厘米)=400(米);
量得学校到汽车站的距离是3厘米,
则学校到汽车站的实际距离是:3÷
=60000(厘米)=600(米);
故答案为:北.西30°.400.南.西50°.600;
(
3
)量得学校到邮电局的图上距离为1厘米,
则学校到邮电局的实际距离为:1÷
=20000(厘米)=200(米);
所以小丽需要的时间为:
(600+200+400)÷50=1200÷50=24(分钟)
答:小丽以每分钟50米的速度步行,从汽车站经过学校.邮局再到中医院大约需要24分钟.
故答案为:24.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
