18.1.2 平行四边形的判定(1)课件(21张)
文档属性
| 名称 | 18.1.2 平行四边形的判定(1)课件(21张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 655.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 12:06:07 | ||
图片预览





文档简介
(共21张PPT)
八年级
下册
18.1.2 平行四边形的判定(1)
平行四边形的定义:两组对边分别平行的四边形叫
做平行四边形.
平行四边形的性质:对边相等,对角相等,对角线
互相平分.
?
判定
性质
定义
D
A
B
C
判定
性质
定义
D
A
B
C
问题 如何寻找平行四边形的判定方法?
当我们对前进的方向感到迷茫时,不妨回过头来看
看走过的路!
直角三角
形的性质
直角三角
形的判定
勾股定理
勾股定理
的逆定理
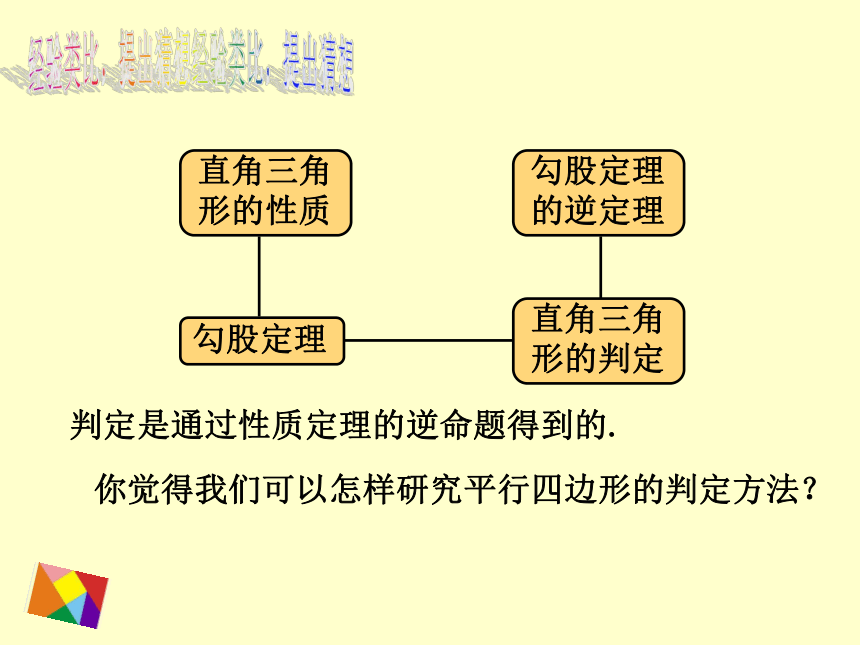
判定是通过性质定理的逆命题得到的.
你觉得我们可以怎样研究平行四边形的判定方法?
两组对边分别相等的
四边形是平行四边形
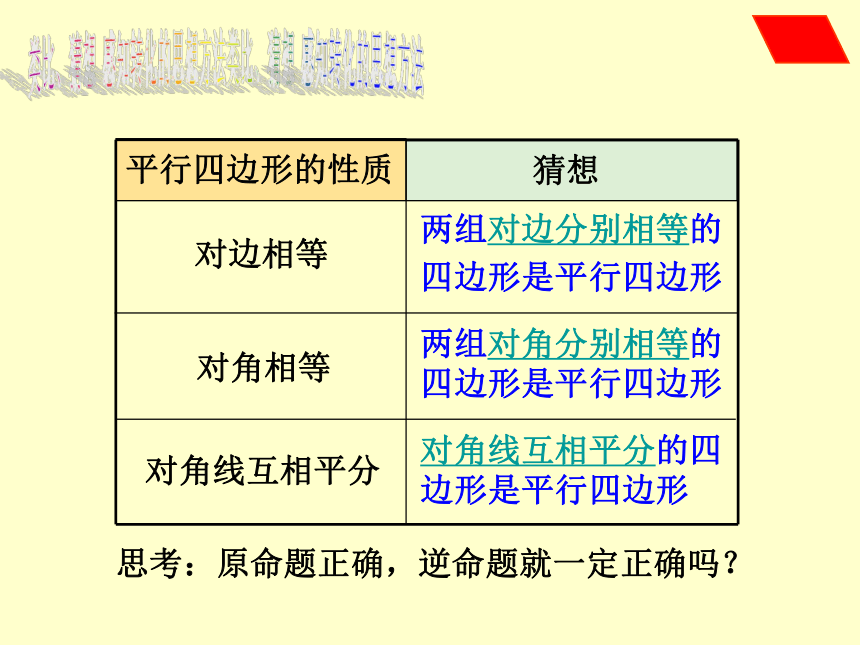
平行四边形的性质
猜想
对边相等
对角相等
对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:原命题正确,逆命题就一定正确吗?
证明:连接BD.
∵ AB=CD,AD=BC,
BD=DB,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
判定定理1
猜想1
D
A
B
C
1
2
3
4
几何语言:在四边形ABCD中,
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形.
判定定理2
猜想2
D
A
B
C
几何语言:在四边形ABCD中,
∵
∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
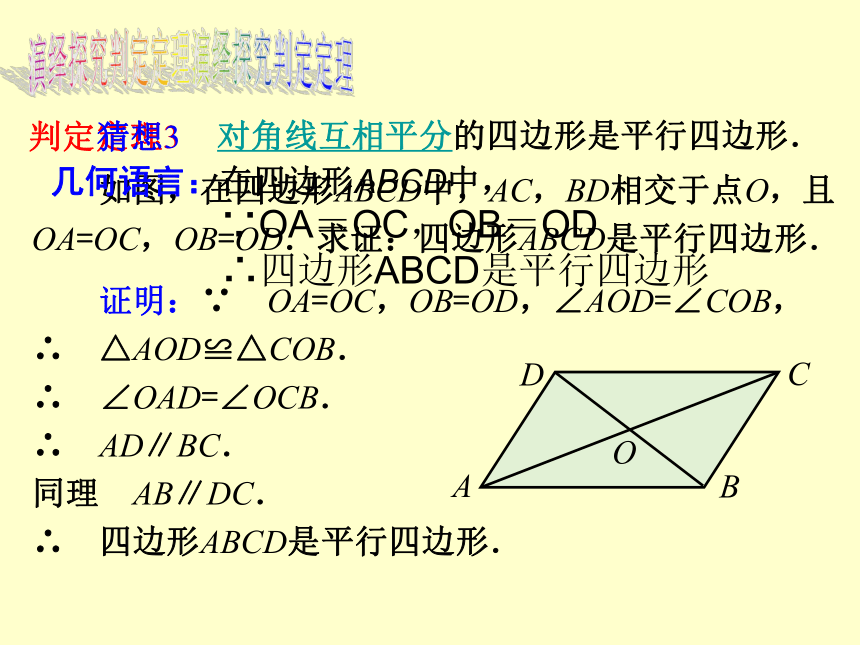
如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
判定定理3
D
A
B
C
O
猜想3
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
几何语言:在四边形ABCD中,
∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
现在,我们一共有哪些判定平行四边形的方法呢?
定义:两组对边分别平行的四边形叫做平行四边形.(边)
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(边)
(2)两组对角分别相等的四边形是平行四边形;
(角)
(3)对角线互相平分的四边形是平行四边形.
(对角线)
这张图揭示了定义、性质、判定间的逻辑关系,提
供了研究几何图形的一般思路.
在研究平行四边形判定的过程中,我们经历了两个
阶段,哪两个阶段呢?
性质
定义
判定
逆向猜想
练习1:如图,在四边形ABCD
中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么
当BC=___?cm,CD=___?cm时,
四边形ABCD为平行四边形;
(2)若AC=6cm,BD=10cm,那么
当AO=___cm,DO=___cm时,
四边形ABCD为平行四边形.
5
3
4
8
例3
如图,
ABCD的对角线AC,BD相交于点O,E,F是对角线AC
上的两点,并且
AE=CF.求证:四边形BFDE是平行四边形.
O
证明:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
又∵AE=CF
∴OA-AE
=OC-CF
∴
OE=OF
∴四边形BFDE是平行四边形
证明:∵四边形ABCD是平行四边形,
∴AD=CB
,
AD∥CB
∴∠DAE=∠BCF
又∵AE=CF
∴△DAE≌△BCF
∴DE=BC
同理BE=DC
∴四边形BFDE是平行四边形
哪一种方法比较简便?
启示:在证明平行四边形时,若条件集中在对角线上,
应用与对角线有关的判定方法解决问题相对简便.分析
问题条件的特点,选择合适的判定方法可以使我们获
得简便的解题方法.
证法二:
A
B
C
D
E
F
O
变一变:如图,平行四边形
ABCD中,E,F分别是对角线AC两侧的延长线上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:连接BD交AC于点O.
∵ABCD是平行四边形
∴OA=OC
OB=OD
又∵AE=CF
∴OA+AE
=OC+CF
∴
OE=OF
∴四边形BFDE是平行四边形
解:图中平行的线段有:AD∥BC,AB∥DC,
DE∥CF,DC∥EF
AB∥EF。
证明:∵ AB=DC,AD=BC,
∴ 四边形ABCD是平行四边形.
∴ AD∥BC,AB∥DC.
又∵ DC=EF,DE=CF,
∴ 四边形DCFE也是平行四边形.
∴ DE∥CF,DC∥EF.
∴ AB∥EF.
练习2:如图,AB=DC=EF,AD=BC,DE=CF.
图中有哪些互相平行的线段?(47页练习1)
A
B
C
D
E
F
练习3:如图,口ABCD的对角线AC、BD相交于点O,E、F分别是OA,OC的中点。求证:BE=DF(47页2题)
【对角线互相平分的四边形是平行四边形】
证明:连接BF,ED
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
∵E,F分别为OA,OC的中点
∴EO=FO
∴四边形EBFD是平行四边形
∴BE=DF
证明:∵ABCD是平行四边形
∴OA=OC
OB=OD
又∵E、F分别是OA、OC的中点。
∴OE=OF
又∠BOE=∠DOF
∴△BOE≌△DOF
∴BE=DF
练习3:
如图,口ABCD的对角线AC、BD相交于点O,E、F分别是OA,OC的中点。求证:BE=DF。
(47页2题)
证法二:
2.我们是如何得到这些判定方法的?研究图形的一般思路?
把平行四边形的判定转化成平行四边形的性质的逆命题
从平行四边形的性质逆向思维,得到逆命题,通过证明得到判定定理.
性质
定义
判定
逆向猜想
1.把你这节课学到的知识及收获和大家分享
3.平行四边形的判定方法?
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)两组对角分别相等的四边形是平行四边形;
(4)对角线互相平分的四边形是平行四边形.
4.如何选用这些方法?
证明平行四边形有多种方法,应根据条件灵活应用.
课内作业:P50
习题18.1
第4,5题.
课外作业:
1.复习背诵4个判定方法.(边、角、对角线)
2.完成相关练习
八年级
下册
18.1.2 平行四边形的判定(1)
平行四边形的定义:两组对边分别平行的四边形叫
做平行四边形.
平行四边形的性质:对边相等,对角相等,对角线
互相平分.
?
判定
性质
定义
D
A
B
C
判定
性质
定义
D
A
B
C
问题 如何寻找平行四边形的判定方法?
当我们对前进的方向感到迷茫时,不妨回过头来看
看走过的路!
直角三角
形的性质
直角三角
形的判定
勾股定理
勾股定理
的逆定理
判定是通过性质定理的逆命题得到的.
你觉得我们可以怎样研究平行四边形的判定方法?
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
猜想
对边相等
对角相等
对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:原命题正确,逆命题就一定正确吗?
证明:连接BD.
∵ AB=CD,AD=BC,
BD=DB,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
判定定理1
猜想1
D
A
B
C
1
2
3
4
几何语言:在四边形ABCD中,
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形.
判定定理2
猜想2
D
A
B
C
几何语言:在四边形ABCD中,
∵
∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
判定定理3
D
A
B
C
O
猜想3
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
几何语言:在四边形ABCD中,
∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
现在,我们一共有哪些判定平行四边形的方法呢?
定义:两组对边分别平行的四边形叫做平行四边形.(边)
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(边)
(2)两组对角分别相等的四边形是平行四边形;
(角)
(3)对角线互相平分的四边形是平行四边形.
(对角线)
这张图揭示了定义、性质、判定间的逻辑关系,提
供了研究几何图形的一般思路.
在研究平行四边形判定的过程中,我们经历了两个
阶段,哪两个阶段呢?
性质
定义
判定
逆向猜想
练习1:如图,在四边形ABCD
中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么
当BC=___?cm,CD=___?cm时,
四边形ABCD为平行四边形;
(2)若AC=6cm,BD=10cm,那么
当AO=___cm,DO=___cm时,
四边形ABCD为平行四边形.
5
3
4
8
例3
如图,
ABCD的对角线AC,BD相交于点O,E,F是对角线AC
上的两点,并且
AE=CF.求证:四边形BFDE是平行四边形.
O
证明:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
又∵AE=CF
∴OA-AE
=OC-CF
∴
OE=OF
∴四边形BFDE是平行四边形
证明:∵四边形ABCD是平行四边形,
∴AD=CB
,
AD∥CB
∴∠DAE=∠BCF
又∵AE=CF
∴△DAE≌△BCF
∴DE=BC
同理BE=DC
∴四边形BFDE是平行四边形
哪一种方法比较简便?
启示:在证明平行四边形时,若条件集中在对角线上,
应用与对角线有关的判定方法解决问题相对简便.分析
问题条件的特点,选择合适的判定方法可以使我们获
得简便的解题方法.
证法二:
A
B
C
D
E
F
O
变一变:如图,平行四边形
ABCD中,E,F分别是对角线AC两侧的延长线上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:连接BD交AC于点O.
∵ABCD是平行四边形
∴OA=OC
OB=OD
又∵AE=CF
∴OA+AE
=OC+CF
∴
OE=OF
∴四边形BFDE是平行四边形
解:图中平行的线段有:AD∥BC,AB∥DC,
DE∥CF,DC∥EF
AB∥EF。
证明:∵ AB=DC,AD=BC,
∴ 四边形ABCD是平行四边形.
∴ AD∥BC,AB∥DC.
又∵ DC=EF,DE=CF,
∴ 四边形DCFE也是平行四边形.
∴ DE∥CF,DC∥EF.
∴ AB∥EF.
练习2:如图,AB=DC=EF,AD=BC,DE=CF.
图中有哪些互相平行的线段?(47页练习1)
A
B
C
D
E
F
练习3:如图,口ABCD的对角线AC、BD相交于点O,E、F分别是OA,OC的中点。求证:BE=DF(47页2题)
【对角线互相平分的四边形是平行四边形】
证明:连接BF,ED
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
∵E,F分别为OA,OC的中点
∴EO=FO
∴四边形EBFD是平行四边形
∴BE=DF
证明:∵ABCD是平行四边形
∴OA=OC
OB=OD
又∵E、F分别是OA、OC的中点。
∴OE=OF
又∠BOE=∠DOF
∴△BOE≌△DOF
∴BE=DF
练习3:
如图,口ABCD的对角线AC、BD相交于点O,E、F分别是OA,OC的中点。求证:BE=DF。
(47页2题)
证法二:
2.我们是如何得到这些判定方法的?研究图形的一般思路?
把平行四边形的判定转化成平行四边形的性质的逆命题
从平行四边形的性质逆向思维,得到逆命题,通过证明得到判定定理.
性质
定义
判定
逆向猜想
1.把你这节课学到的知识及收获和大家分享
3.平行四边形的判定方法?
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)两组对角分别相等的四边形是平行四边形;
(4)对角线互相平分的四边形是平行四边形.
4.如何选用这些方法?
证明平行四边形有多种方法,应根据条件灵活应用.
课内作业:P50
习题18.1
第4,5题.
课外作业:
1.复习背诵4个判定方法.(边、角、对角线)
2.完成相关练习
