2020-2021学年北师大版数学七年级下册2.3.2平行线的性质的综合应用课件(22张)
文档属性
| 名称 | 2020-2021学年北师大版数学七年级下册2.3.2平行线的性质的综合应用课件(22张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 283.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 12:14:18 | ||
图片预览








文档简介
3
第二章
相交线与平行线
平行线的性质
北师大七年级(下)
《数学》(
北师大.七年级
下册
)
强化和练习
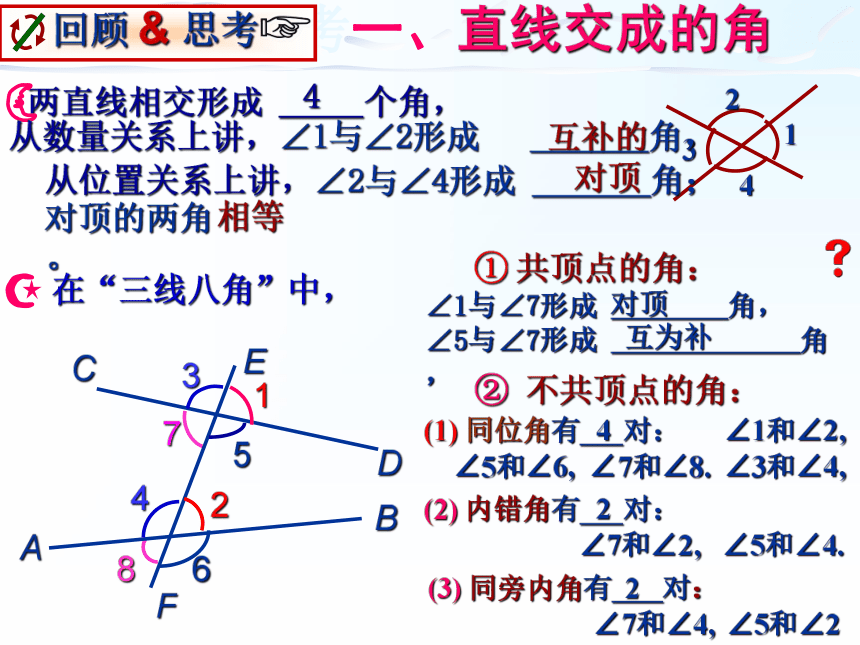
回顾与思考一、直线交成的角
回顾
&
思考
?
两直线相交形成
个角,
1
2
3
4
互补的
从位置关系上讲,∠2与∠4形成
角;
对顶
①
共顶点的角:
∠1与∠7形成
角,
∠5与∠7形成
角,
②
不共顶点的角:
4
从数量关系上讲,∠1与∠2形成
角,
对顶的两角
。
相等
在“三线八角”中,
F
1
3
7
5
2
8
6
D
C
A
B
E
4
对顶
互为补
(1)
同位角有
对:
∠1和∠2,
∠3和∠4,
∠5和∠6,
∠7和∠8.
4
(2)
内错角有
对:
∠7和∠2,
∠5和∠4.
2
(3)
同旁内角有
对:
∠7和∠4,
∠5和∠2
2
1、在同一平面内,不相交的两条直线
4、同位角相等,两直线平行
5、内错角相等,两直线平行
6、同旁内角互补,两直线平行
二、判断两条直线平行的方法有哪些?
2、如果两条直线都与第三条直线平行,那么这两条直线互相平行
3、垂直于同一条直线的两条直线互相平行
1、∵
∠B=∠1
(已知)
∴
AD//BC(
)
2、
∵
∠1=∠D
(已知)
∴
AB//CD
(
)
3、
∵
∠B+∠BCD=180?
(已知)
∴
______________(
)
4、
∵
∠2=∠4
(已知)
∴
____________(
)
5、
∵
_______=_______
(已知)
∴
AB//CD
(
)
三、课堂练习
A
B
C
D
1
2
3
4
5
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
AB
//
CD
内错角相等,两直线平行
AD
//
BC
∠5
∠3
内错角相等,两直线平行
练习:如图当∠1=
∠4时
(
)∥(
);∠
2=∠4时,(
)
∥
(
);
∠
1+∠3=180°
时,(
)∥(
).
l
a
b
m
n
2
1
3
4
分析:∠1=
∠4时,与∠1和∠4有关系的直线如右图(1)
当∠2=
∠4时,与∠2和∠4有关系的直线如右图(2)
a
b
l
1
4
(1)
a
l
m
2
4
(2)
当∠
1+∠3=180°时,与
∠
1和∠3有关系的直线如右图(3)
l
n
b
1
3
(3)
a
b
n
l
l
m
回顾与思考
二、判断两直线平行
回顾
&
思考
?
同位角
,两直线平行.
内错角
,两直线平行.
同旁内角
,两直线平行.
考察两直线是否有平行关系,我们往往用第三直线作为沟通这两直线的桥梁——
考察(被第三直线截成的八个角中)不共顶点的两个角,
是否满足某种数量关系
.
a
b
l
相等
相等
互补
抓住被考察的两直线、寻找第三线;
找出不共顶点的两个角及其数量关系,
是判定两直线平行的必要途径。
新知探索:
二直线平行后得到什么?
b
a
c
如图:直线
a
与b
直线平行。
(1)测量同位角∠1和∠5的大小,它们有什么关系?
相等:∠1=∠5。
图中还有其它同位角吗?
它们的大小有什么关系?
∠2=∠6、
∠3=∠7、
∠4=∠8;
还有三对同位角。
(2)图中有几对内错角?它们的大小有什么关系?为什么?
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
有两对内错角:
∠3=∠5、
∠4=∠6;
∵∠4=∠2,∠2=∠6,
∴
∠4=∠6。
同理:
∠3=∠5
有两对同旁内角:
∠4+∠5=180°,
∠3+∠6=180°。
从中,你发现了什么规律吗?
8
3
1
2
4
5
7
6
简记为:
规律
两条平行直线被第三条直线直线所截,
两直线平行,内错角相等。
两直线平行,同旁内角互补。
两直线平行,同位角相等。
二平行直线的特征
(性质)
同位角相等,内错角相等,同旁内角互补。
两类定理的比较
两条平行直线被第三条直线直线所截,
同位角相等,
两直线平行
两直线平行,同位角相等。
判定定理
性质定理
条件
结论
条件
结论
思考:
1、判定定理与性质定理的
条件与结论有什么关系?
互换。
内错角相等,
两直线平行
两直线平行,内错角相等。
同旁内角互补,两直线平行
两直线平行,同旁内角互补
2、使用判定定理时是
已知
,说明
角的相等或互补
二直线平行
使用性质定理时是
已知
,说明
。
二直线平行
角的相等或互补
眼睛1
眼睛2
视线
北
北
甲
乙
42°
你还能举出哪
些生活中的实
际事例吗?
如图,AB∥CD,∠B=∠D,比较∠A
和∠C的大小,你是怎样得到结论的?
A
B
C
D
AB∥CD
∠A+
∠D=180°
∠C+
∠B=180°
∠A=∠C
如图,AB∥CD,∠B=∠D,比较∠A
和∠C的大小,你是怎样得到结论的?
AD∥BC吗?
A
B
C
D
AB∥CD
∠A+
∠D=180°
∠B=∠D
∠A+∠B=180°
AD∥BC
做一做
P
50
如图:一束平行光线AB和DE射向一个水平镜面后被反射,
(1
)∠1,∠3的大小有什么关系?
∠2与∠4呢?
∵AB∥DE
∴∠1=∠3。
相等:∠3=∠4;
你知道理由吗?
两直线平行
同位角相等
(2
)反射光线BC与EF也平行吗?
∵
∠2=∠4
∴
BC∥EF
。
平行:
又
∠1=∠2
,∠3=∠4
∴
∠2=∠4。
A
B
D
E
C
F
此时∠1=∠2
,
∠3=∠4
。
1
3
2
4
∠2
=∠4
。
你知道理由吗?
同位角相等
两直线平行
∠1=∠2
∠3=∠4
三、随堂练习
p51
1、如图所示,AB∥CD,AC∥BD。
分别找出与∠1相等或互补的角。
如图,与∠1相等的角有:
∠3,
∠5,
∠7,
∠9,
∠11,
∠13,
∠15;
与∠1互补的角有:
∠2,
∠4,
∠6,
∠8,
∠10,
∠12,
∠14,
∠16
;
解:
1
14
16
13
15
3
A
B
D
C
2
4
5
6
7
8
9
10
12
11
(2)如图,已知∠2=∠3,
则(
)∥(
),若AB∥CD,
则∠1=(
)
.
A
B
C
D
1
2
3
4
答案:AD∥BC,
∠1=∠4
如图,已知AG//CF,AB//CD,∠A=40?,求∠C的度数。
F
A
B
C
D
E
G
解:
∵
AG//CF(已知)
∴
∠
A=∠AEC
(两直线平行,内错角相等)
∵
AB//CD
(已知)
∴
∠
C=∠AEC
(根据两直线平行,内错角相等)
∴
∠C
=
∠A=40?
∵
∠A=40?
∴
∠C
=
∠A
例1:如图,已知AG//CF,AB//CD,∠A=40?,求∠C的度数。
F
A
B
C
D
E
G
1
解:
∵
AG//CF(已知)
∴
∠A=∠1
(两直线平行,同位角相等)
又∵AB//CD(已知)
∴
∠1=∠C
(两直线平行,同位角相等)
∴
∠A=∠C
(等量代换)
∵
∠A=40?
∴
∠C=40?
例:如图,在四边形ABCD中,已知AB//CD,∠B=60?,
求∠C
的度数。能否求得∠A的度数?
A
B
C
D
解:∵AB//CD
(已知)
∴∠B+∠C=180°
(根据两直线,
同旁内角互补)
∵∠B=60°
∴
∠C=180
°
-
∠B
=120
°
根据已知条件,无法求得∠A的度数。
思考题:
如图:如果AB//ED,∠B、∠C、∠D的和是多少?
A
B
C
D
E
c
d
a
b
3
4
2
1
例2
如图所示
∠1
=∠2
求证
:
∠3
=∠4
证明:∵
∠1
=∠2(已知)
∴a//b
(同位角相等,两直线平行)
∴
∠3
=∠4
(两直线平行,内错角相等)
小结
四、本节课你的收获是什么?
本节课你学到了什么?
本节课初步学习了如何混合应用平行线的判定与性质进行计算和说理(证明).
要懂得几何中的计算往往要说理,要熟悉几何里计算题的格式;
还要懂得几何中常常可以由“已知”的条件推得一系列新的结论,在这个过程中,要能清楚每一步推理的依据,并初步了解解答这类问题的格式和要求.
本节课学行线的三个性质,总结了平行线的判定
与性
质的区别.
这里的关键之一是要搞清“已知”了什么,得到的是什么样的“结论”.这样才能确保正确的应用,不发生错误.
课后作业
课本P51页
习题2.5
课本P54页
习题2.6
第二章
相交线与平行线
平行线的性质
北师大七年级(下)
《数学》(
北师大.七年级
下册
)
强化和练习
回顾与思考一、直线交成的角
回顾
&
思考
?
两直线相交形成
个角,
1
2
3
4
互补的
从位置关系上讲,∠2与∠4形成
角;
对顶
①
共顶点的角:
∠1与∠7形成
角,
∠5与∠7形成
角,
②
不共顶点的角:
4
从数量关系上讲,∠1与∠2形成
角,
对顶的两角
。
相等
在“三线八角”中,
F
1
3
7
5
2
8
6
D
C
A
B
E
4
对顶
互为补
(1)
同位角有
对:
∠1和∠2,
∠3和∠4,
∠5和∠6,
∠7和∠8.
4
(2)
内错角有
对:
∠7和∠2,
∠5和∠4.
2
(3)
同旁内角有
对:
∠7和∠4,
∠5和∠2
2
1、在同一平面内,不相交的两条直线
4、同位角相等,两直线平行
5、内错角相等,两直线平行
6、同旁内角互补,两直线平行
二、判断两条直线平行的方法有哪些?
2、如果两条直线都与第三条直线平行,那么这两条直线互相平行
3、垂直于同一条直线的两条直线互相平行
1、∵
∠B=∠1
(已知)
∴
AD//BC(
)
2、
∵
∠1=∠D
(已知)
∴
AB//CD
(
)
3、
∵
∠B+∠BCD=180?
(已知)
∴
______________(
)
4、
∵
∠2=∠4
(已知)
∴
____________(
)
5、
∵
_______=_______
(已知)
∴
AB//CD
(
)
三、课堂练习
A
B
C
D
1
2
3
4
5
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
AB
//
CD
内错角相等,两直线平行
AD
//
BC
∠5
∠3
内错角相等,两直线平行
练习:如图当∠1=
∠4时
(
)∥(
);∠
2=∠4时,(
)
∥
(
);
∠
1+∠3=180°
时,(
)∥(
).
l
a
b
m
n
2
1
3
4
分析:∠1=
∠4时,与∠1和∠4有关系的直线如右图(1)
当∠2=
∠4时,与∠2和∠4有关系的直线如右图(2)
a
b
l
1
4
(1)
a
l
m
2
4
(2)
当∠
1+∠3=180°时,与
∠
1和∠3有关系的直线如右图(3)
l
n
b
1
3
(3)
a
b
n
l
l
m
回顾与思考
二、判断两直线平行
回顾
&
思考
?
同位角
,两直线平行.
内错角
,两直线平行.
同旁内角
,两直线平行.
考察两直线是否有平行关系,我们往往用第三直线作为沟通这两直线的桥梁——
考察(被第三直线截成的八个角中)不共顶点的两个角,
是否满足某种数量关系
.
a
b
l
相等
相等
互补
抓住被考察的两直线、寻找第三线;
找出不共顶点的两个角及其数量关系,
是判定两直线平行的必要途径。
新知探索:
二直线平行后得到什么?
b
a
c
如图:直线
a
与b
直线平行。
(1)测量同位角∠1和∠5的大小,它们有什么关系?
相等:∠1=∠5。
图中还有其它同位角吗?
它们的大小有什么关系?
∠2=∠6、
∠3=∠7、
∠4=∠8;
还有三对同位角。
(2)图中有几对内错角?它们的大小有什么关系?为什么?
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
有两对内错角:
∠3=∠5、
∠4=∠6;
∵∠4=∠2,∠2=∠6,
∴
∠4=∠6。
同理:
∠3=∠5
有两对同旁内角:
∠4+∠5=180°,
∠3+∠6=180°。
从中,你发现了什么规律吗?
8
3
1
2
4
5
7
6
简记为:
规律
两条平行直线被第三条直线直线所截,
两直线平行,内错角相等。
两直线平行,同旁内角互补。
两直线平行,同位角相等。
二平行直线的特征
(性质)
同位角相等,内错角相等,同旁内角互补。
两类定理的比较
两条平行直线被第三条直线直线所截,
同位角相等,
两直线平行
两直线平行,同位角相等。
判定定理
性质定理
条件
结论
条件
结论
思考:
1、判定定理与性质定理的
条件与结论有什么关系?
互换。
内错角相等,
两直线平行
两直线平行,内错角相等。
同旁内角互补,两直线平行
两直线平行,同旁内角互补
2、使用判定定理时是
已知
,说明
角的相等或互补
二直线平行
使用性质定理时是
已知
,说明
。
二直线平行
角的相等或互补
眼睛1
眼睛2
视线
北
北
甲
乙
42°
你还能举出哪
些生活中的实
际事例吗?
如图,AB∥CD,∠B=∠D,比较∠A
和∠C的大小,你是怎样得到结论的?
A
B
C
D
AB∥CD
∠A+
∠D=180°
∠C+
∠B=180°
∠A=∠C
如图,AB∥CD,∠B=∠D,比较∠A
和∠C的大小,你是怎样得到结论的?
AD∥BC吗?
A
B
C
D
AB∥CD
∠A+
∠D=180°
∠B=∠D
∠A+∠B=180°
AD∥BC
做一做
P
50
如图:一束平行光线AB和DE射向一个水平镜面后被反射,
(1
)∠1,∠3的大小有什么关系?
∠2与∠4呢?
∵AB∥DE
∴∠1=∠3。
相等:∠3=∠4;
你知道理由吗?
两直线平行
同位角相等
(2
)反射光线BC与EF也平行吗?
∵
∠2=∠4
∴
BC∥EF
。
平行:
又
∠1=∠2
,∠3=∠4
∴
∠2=∠4。
A
B
D
E
C
F
此时∠1=∠2
,
∠3=∠4
。
1
3
2
4
∠2
=∠4
。
你知道理由吗?
同位角相等
两直线平行
∠1=∠2
∠3=∠4
三、随堂练习
p51
1、如图所示,AB∥CD,AC∥BD。
分别找出与∠1相等或互补的角。
如图,与∠1相等的角有:
∠3,
∠5,
∠7,
∠9,
∠11,
∠13,
∠15;
与∠1互补的角有:
∠2,
∠4,
∠6,
∠8,
∠10,
∠12,
∠14,
∠16
;
解:
1
14
16
13
15
3
A
B
D
C
2
4
5
6
7
8
9
10
12
11
(2)如图,已知∠2=∠3,
则(
)∥(
),若AB∥CD,
则∠1=(
)
.
A
B
C
D
1
2
3
4
答案:AD∥BC,
∠1=∠4
如图,已知AG//CF,AB//CD,∠A=40?,求∠C的度数。
F
A
B
C
D
E
G
解:
∵
AG//CF(已知)
∴
∠
A=∠AEC
(两直线平行,内错角相等)
∵
AB//CD
(已知)
∴
∠
C=∠AEC
(根据两直线平行,内错角相等)
∴
∠C
=
∠A=40?
∵
∠A=40?
∴
∠C
=
∠A
例1:如图,已知AG//CF,AB//CD,∠A=40?,求∠C的度数。
F
A
B
C
D
E
G
1
解:
∵
AG//CF(已知)
∴
∠A=∠1
(两直线平行,同位角相等)
又∵AB//CD(已知)
∴
∠1=∠C
(两直线平行,同位角相等)
∴
∠A=∠C
(等量代换)
∵
∠A=40?
∴
∠C=40?
例:如图,在四边形ABCD中,已知AB//CD,∠B=60?,
求∠C
的度数。能否求得∠A的度数?
A
B
C
D
解:∵AB//CD
(已知)
∴∠B+∠C=180°
(根据两直线,
同旁内角互补)
∵∠B=60°
∴
∠C=180
°
-
∠B
=120
°
根据已知条件,无法求得∠A的度数。
思考题:
如图:如果AB//ED,∠B、∠C、∠D的和是多少?
A
B
C
D
E
c
d
a
b
3
4
2
1
例2
如图所示
∠1
=∠2
求证
:
∠3
=∠4
证明:∵
∠1
=∠2(已知)
∴a//b
(同位角相等,两直线平行)
∴
∠3
=∠4
(两直线平行,内错角相等)
小结
四、本节课你的收获是什么?
本节课你学到了什么?
本节课初步学习了如何混合应用平行线的判定与性质进行计算和说理(证明).
要懂得几何中的计算往往要说理,要熟悉几何里计算题的格式;
还要懂得几何中常常可以由“已知”的条件推得一系列新的结论,在这个过程中,要能清楚每一步推理的依据,并初步了解解答这类问题的格式和要求.
本节课学行线的三个性质,总结了平行线的判定
与性
质的区别.
这里的关键之一是要搞清“已知”了什么,得到的是什么样的“结论”.这样才能确保正确的应用,不发生错误.
课后作业
课本P51页
习题2.5
课本P54页
习题2.6
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
