《三角形的内角和》练习

《三角形的内角和》练习
【例题分析】
例1. 在△ABC中，已知∠A＝∠B＝∠C，请你判断三角形的形状。
　　分析：三角形的形状按边分和按角分两类，本题由于不可能按边分，因此只有计算各角的度数，按角来确定形状，由于在该题中∠C是最大的角，因此只需求出∠C的度数即可判断三角形的形状。
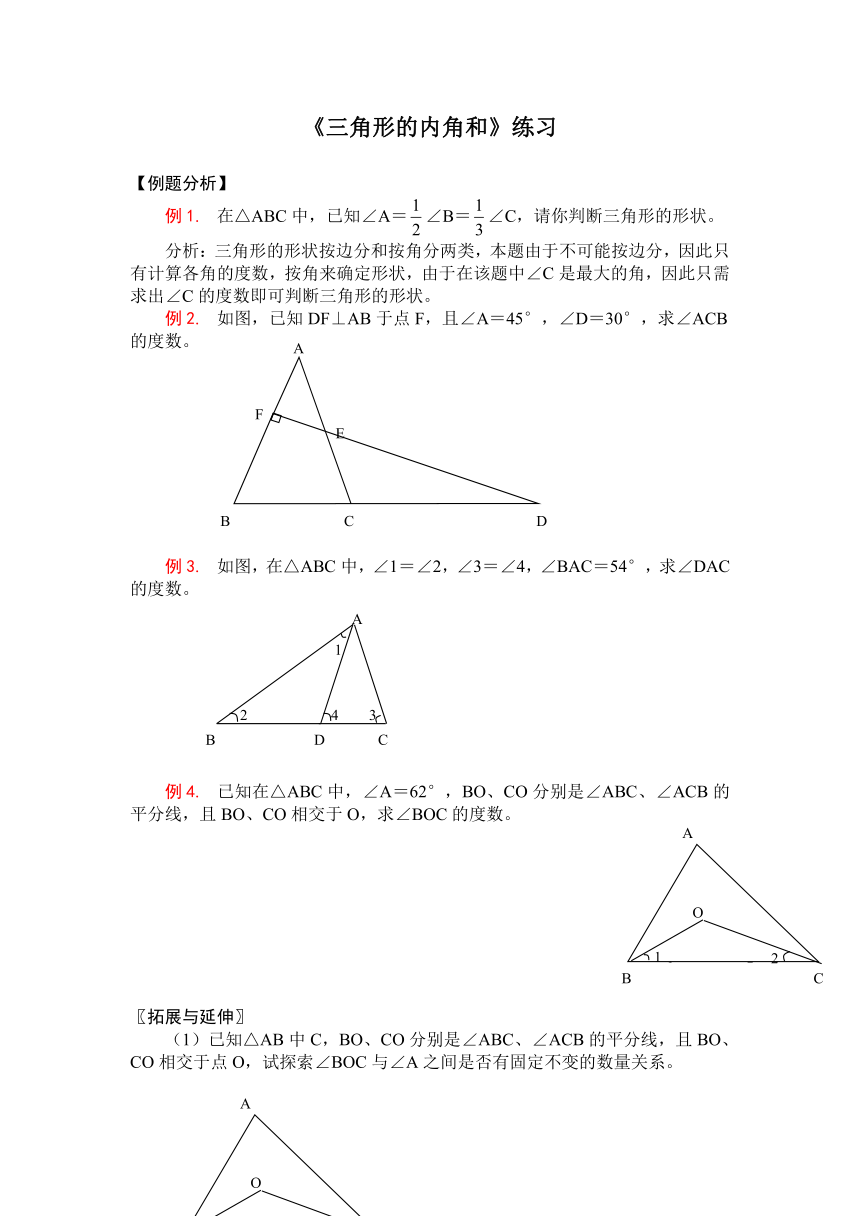
例2. 如图，已知DF⊥AB于点F，且∠A＝45°，∠D＝30°，求∠ACB的度数。
例3. 如图，在△ABC中，∠1＝∠2，∠3＝∠4，∠BAC＝54°，求∠DAC的度数。
例4. 已知在△ABC中，∠A＝62°，BO、CO分别是∠ABC、∠ACB的平分线，且BO、CO相交于O，求∠BOC的度数。
〖拓展与延伸〗
（1）已知△AB中C，BO、CO分别是∠ABC、∠ACB的平分线，且BO、CO相交于点O，试探索∠BOC与∠A之间是否有固定不变的数量关系。
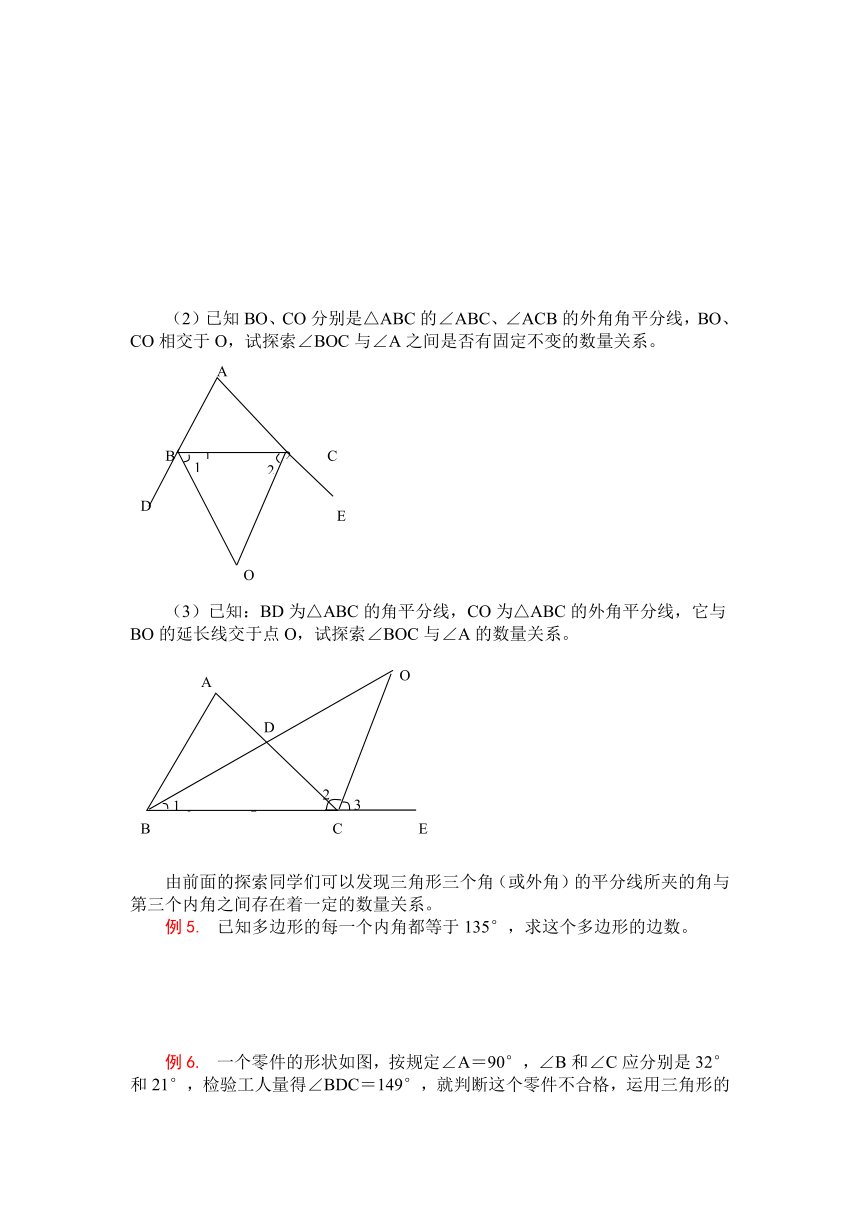
（2）已知BO、CO分别是△ABC的∠ABC、∠ACB的外角角平分线，BO、CO相交于O，试探索∠BOC与∠A之间是否有固定不变的数量关系。
（3）已知：BD为△ABC的角平分线，CO为△ABC的外角平分线，它与BO的延长线交于点O，试探索∠BOC与∠A的数量关系。
　　由前面的探索同学们可以发现三角形三个角（或外角）的平分线所夹的角与第三个内角之间存在着一定的数量关系。
已知多边形的每一个内角都等于135°，求这个多边形的边数。
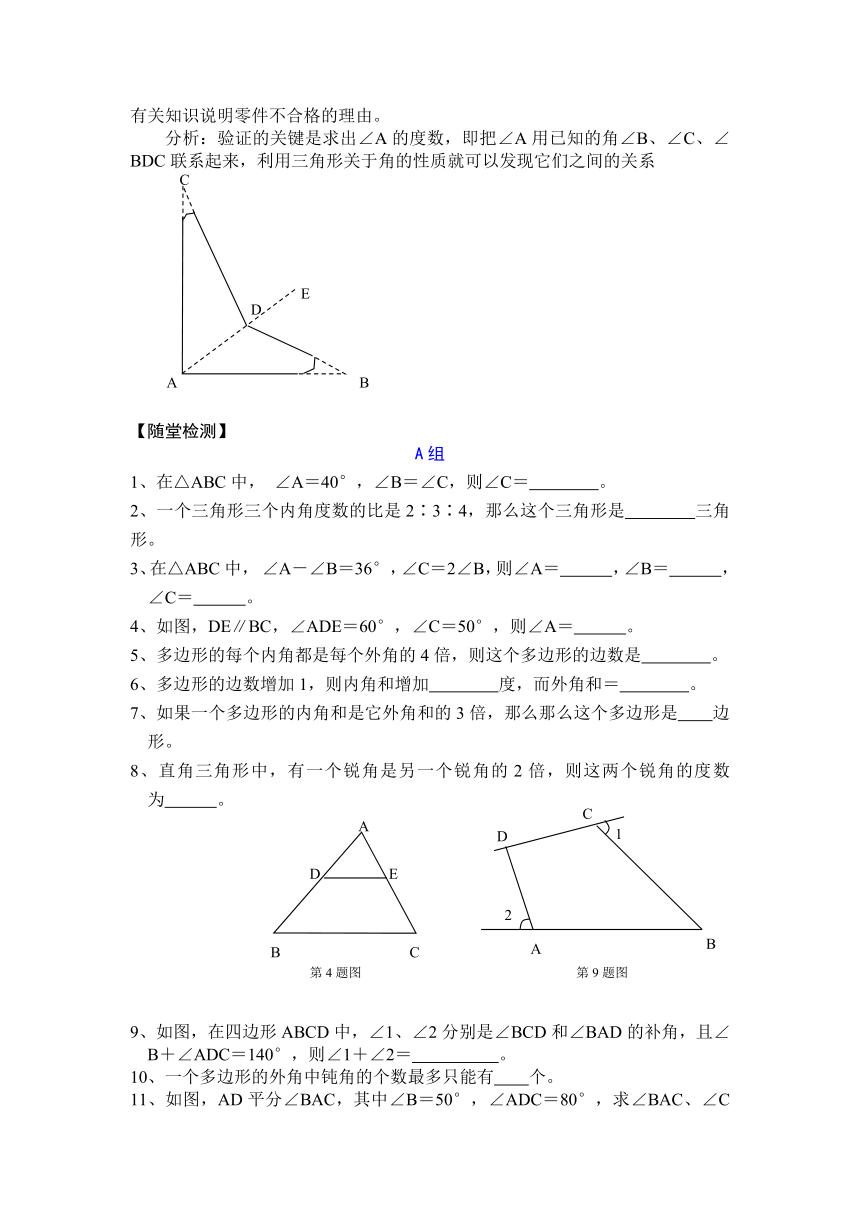
例6.　一个零件的形状如图，按规定∠A＝90°，∠B和∠C应分别是32°和21°，检验工人量得∠BDC＝149°，就判断这个零件不合格，运用三角形的有关知识说明零件不合格的理由。
分析：验证的关键是求出∠A的度数，即把∠A用已知的角∠B、∠C、∠BDC联系起来，利用三角形关于角的性质就可以发现它们之间的关系
【随堂检测】
A组
1、在△ABC中， ∠A＝40°，∠B＝∠C，则∠C＝　　　　。
2、一个三角形三个内角度数的比是2∶3∶4，那么这个三角形是　　　　三角形。
3、在△ABC中， ∠A－∠B＝36°，∠C＝2∠B，则∠A＝　　　，∠B＝　　　，∠C＝　　　。
4、如图，DE∥BC，∠ADE＝60°，∠C＝50°，则∠A＝　　　。
5、多边形的每个内角都是每个外角的4倍，则这个多边形的边数是　　　　。
6、多边形的边数增加1，则内角和增加　　　　度，而外角和＝　　　　。
7、如果一个多边形的内角和是它外角和的3倍，那么那么这个多边形是　　边形。
8、直角三角形中，有一个锐角是另一个锐角的2倍，则这两个锐角的度数为　　　。
9、如图，在四边形ABCD中，∠1、∠2分别是∠BCD和∠BAD的补角，且∠B＋∠ADC＝140°，则∠1＋∠2＝　　　　　。
10、一个多边形的外角中钝角的个数最多只能有　　个。
11、如图，AD平分∠BAC，其中∠B＝50°，∠ADC＝80°，求∠BAC、∠C的度数。
12、如图，已知∠B＝40°，∠C＝59°，∠DEC＝47°，求∠F的度数。
13、如图，求∠α的度数。
　　
14、如图，已知△ABC中，已知∠B＝65°，∠C＝45°，AD是BC边上的高，AE是∠BAC的平分线，求∠DAE的度数。
B组
1、如图，与∠FDB成内错角的是　　　　，与∠DFB成同旁内角的是　　　　　　。
2、如图，D是AB上一点，CE∥BD，CB∥ED，EA⊥BA于A，若∠ABC＝38°，则∠AED＝　　　　　。
3、在△ABC中，∠A＝40°，∠B－∠C＝60°，则∠C＝　　　，按角分，这是　　　　三角形。
4、若一个三角形的两边长分别为1，2，第三边长为整数，则第三边长为　　　。
5、如图，△ABC平移后的图形为△EDF，∠B的对应角是　　　，线段AC的对应线段是　　　　，点C的对应点是　　　，△ABC平移的方向是点A到点　　的方向，平移的距离是线段　　　的长度。
6、在四边形ABCD中，若∠A＝∠C＝90°,2∠B＝3∠D，则∠B＝　　　，∠D＝　　　.
7、若一个多边形的内角和等于1260°，则这个多边形是　　　边形。
8、如果一个多边形的每一个内角都等于108°，则这个多边形是　　　边形。
9、若两条直线被第三条直线所截，则（　　）
　A、同位角相等　　　　　B、内错角相等
　C、同旁内角互补　　　　D、以上结论都不对
10、如图，图中的内错角共有　（　　）
　A、4对　　　　B、5对　　　　C、6对　　　　D、7对
11、在同一平面内三条直线a、b、c满足关系a⊥b，b⊥c，那么（　　）
　A、a∥c　　　B、a⊥c　　　C、a与c相交但不垂直　　　D、以上都不对
12、下列运动中，不属于平移的有（　　）
　①鱼的游动　②开门时门的移动　③拉抽屉时的抽屉　④工厂里的输送带
　A、4个　　　B、3个　　　C、2个　　　D、1个
13、在一个三角形ABC中，∠A＝∠B＝45°，则△ABC是（　　）
　A、直角三角形　　B、锐角三角形　　C、钝角三角形　　　D、以上都不对
14、已知三角形的三边分别为2，a、4，那么a的范围是（　　）
　A、1＜a＜5　　　B、2＜a＜6　　　C、3＜a＜7　　　D、4＜a＜6
15、如图，已知AD∥BC且DC⊥AD于D，试证明：
　（1）DC⊥BC　　　（2）∠1＋∠2＝180°
16、如图，在四边形ABCD中，AD∥BC，且AD＜BC，AC、BD为两条对角线，且AC⊥BD，AC＝BD，
　（1）把AC平移到DE的位置，方向为射线AD的方向，平移的距离为线段AD的长。
　（2）判断△BDE的形状。
17、如图，AB∥DE，CM平分∠BCE，CN⊥CM，∠B＝60°，求∠DCN的度数。
F　　　　　　
E　　　　　　
A　　　　　　
B　　　　　　　 C　　　　　　　　　　　　D
B　　　　　　 D　 C
2　　　　　 4　 3
1　　　　
A　　　　
1　　　　　2
B　　　　　　　　　　　　C
A　　
O
1　
2
1　　　　　2
B　　　　　　　　　　　　C
A　　
O
1　
2
B　　　　　　　　　　C
A　　
O
1　
2
D　　
1　　　　　2
E
1　　　　2
B　　　　　　　　　　　　C　　　　　E
A　　
O
1　
2
3
D
A　　　　　　　　　　　　B
D　　　　　　　　　　　B
E　　　　　　　　　　B
C　　　　　　　　　B
B　　　　　　　　 C
D　　　　 E
A　　　　 C
第4题图 　　　　　第9题图
A
2
1
B
C
D
B　　　　　　　D　　　　　　C
A　　　　　
B　　　　　　　D　　　　　C
A　　　　　　　D　　　　　C
E　　　　　　　D　　　　　C
F　　　　　　　D　　　　　C
106°
110°
78°
α
B　　　　 D E C
A　　　　 D E C
B　　　　　　　　　　C
F　　　　　E　
A　　
D　　
B　　　　　　　　 D A
C　　　　　　　 E
B D 　　 C　 F　　
A
E
第1题　　　　　　　　　　　　第2题　　　　　　　　　　　第5题
l1
l2
l3
第10题
B　　　　 4 C
2　　　
5　　　
3　　　
D　　　
1　　　
A　　　
A　　　　　　D
B　　　　　　　　　　　C E
E　　　　　　　C　　　　D
M　　　
N　　　
A　　　　　　　B