2020-2021学年八年级数学人教版下册18.2.1.2矩形的判定课件(共25张)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册18.2.1.2矩形的判定课件(共25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
人教版数学教材八年级下
18.2特殊的平行四边形
18.2.1矩形的判定
一起放飞理想的翅膀
在知识的天空中自由翱翔
新源六中
刘辉强
1、理解并掌握矩形的判定方法。
2、会用矩形判定定理进行有关的论证或计算。
掌握矩形的判定方法及其应用
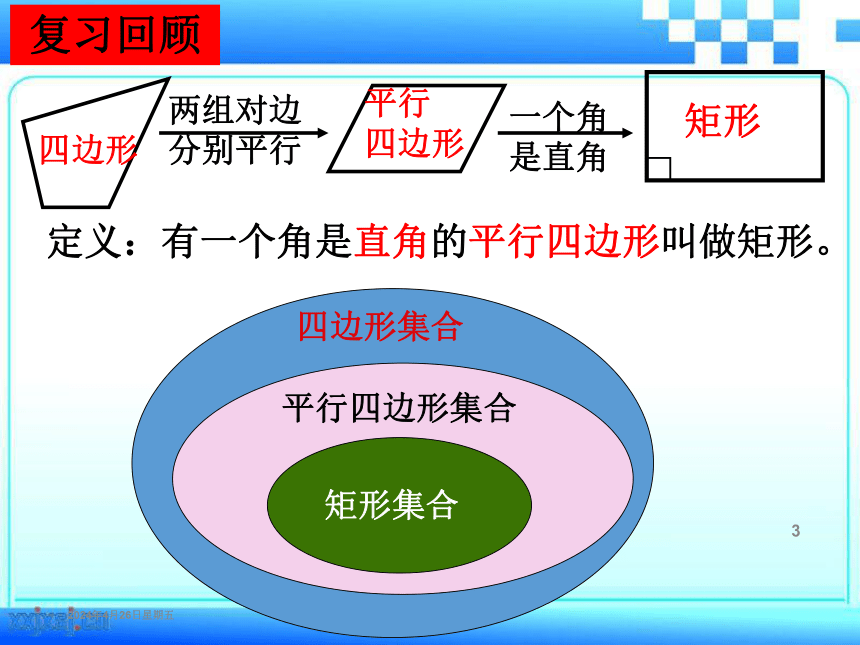
复习回顾
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
∟
矩形
四边形集合
平行四边形集合
矩形集合
定义:有一个角是直角的平行四边形叫做矩形。
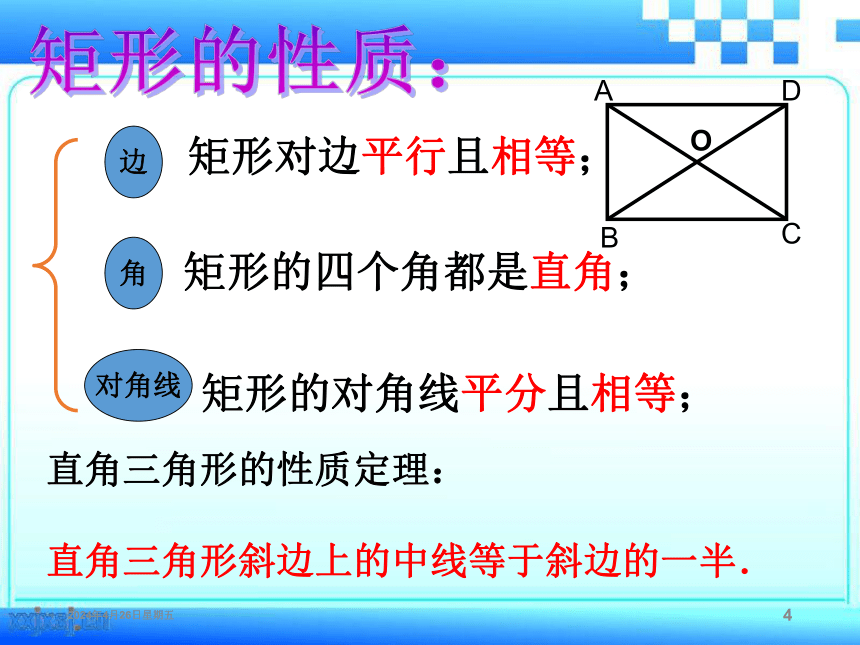
边
对角线
角
A
B
C
D
O
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线平分且相等;
直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
矩形的定义:
有一个角是直角的平行四边形是矩形。
你还有其它的判定方法吗?
ABCD
∠A=900
四边形ABCD是矩形
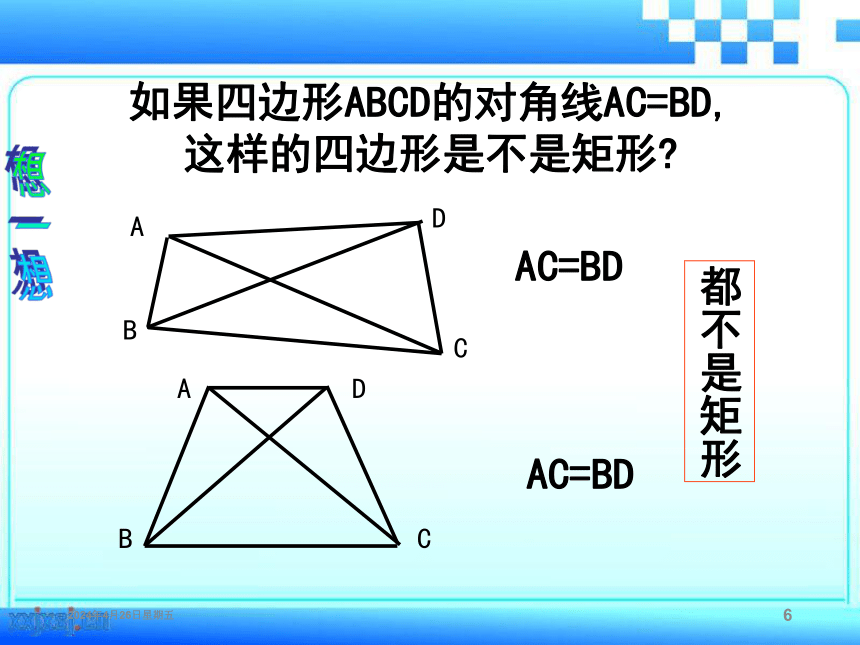
如果四边形ABCD的对角线AC=BD,这样的四边形是不是矩形?
A
B
C
D
AC=BD
A
B
C
D
AC=BD
都不是矩形
O
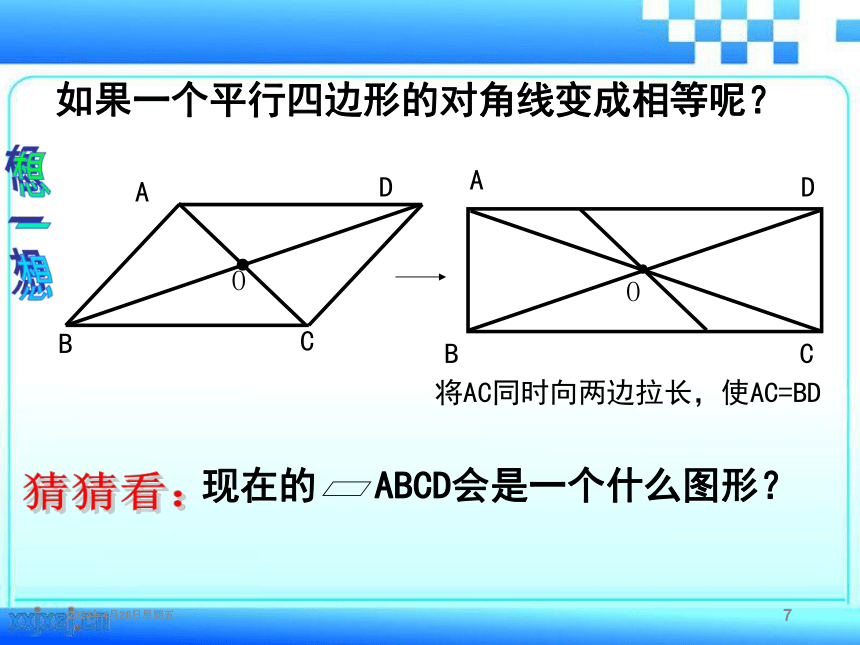
如果一个平行四边形的对角线变成相等呢?
A
B
C
D
将AC同时向两边拉长,使AC=BD
O
A
B
C
D
现在的
ABCD会是一个什么图形?
情境一:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形
。
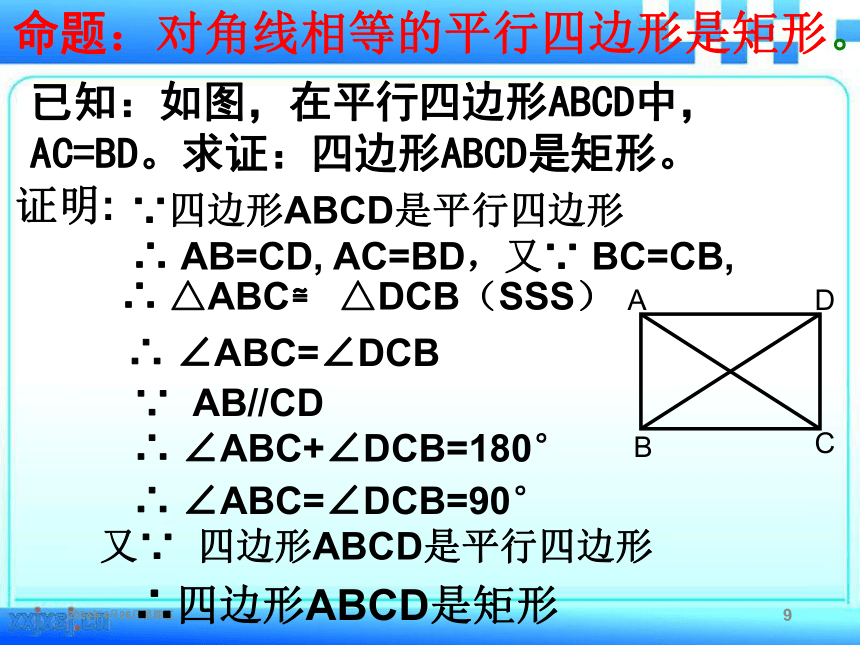
命题:对角线相等的平行四边形是矩形。
已知:如图,在平行四边形ABCD中,AC=BD。求证:四边形ABCD是矩形。
A
B
C
D
证明:
∵四边形ABCD是平行四边形
∴
AB=CD,
AC=BD,又∵
BC=CB,
∴
△ABC≌
△DCB(SSS)
∵
AB//CD
∴
∠ABC+∠DCB=180°
∴
∠ABC=∠DCB=90°
又∵
四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴
∠ABC=∠DCB
对角线相等的平行四边形是矩形
。
矩形的判定方法:
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
A
B
C
D
O
有一个角是直角
有两个角是直角
的
四边形是矩形吗?
有三个角是直角
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
情境一:李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有三个角是直角的四边形是矩形
。
你能证明上述结论吗?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°求证:四边形ABCD是矩形。
A
B
C
D
∟
∟
∟
证明:∵
∠A=∠B=90°
∴
∠A+∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD是平行四边形
又∵
∠A=90°
∴四边形ABCD是矩形
命题:有三个角是直角的四边形是矩形
矩形的判定方法:
有三个角是直角的四边形是矩形
。
A
B
C
D
∵
∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形
。
有三个角是直角的四边形是矩形
。
方法1:
方法2:
方法3:
例1:如图,在平行四边形ABCD中,对角线AC,BD
相交于点O,且OA=OD,
∠OAD=50°,
求:
∠OAB的度数.
范例解析,当堂练习
解:∵四边形ABCD是平行四边形
又∵OA=OD
∴AC=BD
∴四边形ABCD是矩形
A
B
C
D
O
∴∠DAB=90°
又∠OAD=50°
∴
∠OAB=40°
练一练
:
ABCD中,AC,BD交于
点O,△ABO为正三角形,AB=4cm.
求平行四边形的面积.
A
B
C
D
O
4
例2:1.BD、BE分别是∠ABC与它的邻补角的平分线,AE⊥BE,AD⊥BD,
求证:四边形AEBD是矩形。
证明:∵
AE⊥BE,AD⊥BD
∴
∠E=90°,
∠D=90°
∵
BD,BE分别是∠ABC与它的邻补角∠CBP的平分线
∴∠1=
∠ABC,∠2=
∠ABP
∴
□
AEBD是矩形
C
B
A
D
E
P
∟
∟
⌒
⌒
1
2
∴
∠1+∠2=
(∠ABC+∠ABP)=
×180°=90°
即∠DBE=90°
练测促学:1、下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
A
B
D
C
H
E
F
G
∵四边形ABCD是平行四边形
∴∠DAB+∠ABC=180
°
2、如图,
ABCD四个内角的平分线围成四边形EFGH,猜想四边形EFGH的形状,并说明理由
证明:
同理:∠EFG=90°、∠FGH=90°
∴四边形EFGH是矩形
∵AE、BE分别平分∠DAB、∠ABC
∴∠EAB+∠EBA=90
°
即∠AEB=90°
∴∠HEF=90°
3、如图,平行四边形ABCD中,AB=
6,BC=
8,AC=
10
,
求证
:
四边形ABCD是矩形。
D
B
C
A
证明:
∵AB=6,BC=8,AC=10
∴AB2+BC2=62+82=100=102=AC2
∴
∠B=90°
又∵
四边形ABCD是平行四边形
∴
□
ABCD是矩形
拓展延伸:如图,在△ABC中,点0是AC边上的一个动点,过点0作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,
A
B
C
M
N
0
)
1
)
2
(
5
(
4
(
3
(
6
(1)求证:0E=0F
(2)当0运动到何处时,
四边形AECF为矩形?
说明理由
E
F
证明:∵CF平分∠ACD
∴∠1=∠2
又∵
MN∥BC
∴∠1=∠3
∴
∠2=∠3
∴OC=OF
同理可证:OC=OE
∴OE=OF
D
答:当点0为AC的中点时,
四边形AECF是矩形
理由:由(1)知0E=0F,
又AO=CO
∴四边形AECF是平行四边形
又∵EC平分∠ACB,FC平分∠ACD
∴∠2+∠4=90°即∠ECF=90°
∴四边形AECF是矩形
∠A=
∠B=
∠C=90°
ABCD
AC
=
BD
ABCD
∠A=90°
ABCD
是矩形
四边形ABCD
是矩形
谈一谈,今天你有何收获?
判定一个四边形是矩形的方法是:
本节课我们学习了什么内容,你能总结吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形
。
有三个角是直角的四边形是矩形
。
方法1:
方法2:
方法3:
P55
练习2题
P60
习题第1、2题
作业:
人教版数学教材八年级下
18.2特殊的平行四边形
18.2.1矩形的判定
一起放飞理想的翅膀
在知识的天空中自由翱翔
新源六中
刘辉强
1、理解并掌握矩形的判定方法。
2、会用矩形判定定理进行有关的论证或计算。
掌握矩形的判定方法及其应用
复习回顾
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
∟
矩形
四边形集合
平行四边形集合
矩形集合
定义:有一个角是直角的平行四边形叫做矩形。
边
对角线
角
A
B
C
D
O
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线平分且相等;
直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
矩形的定义:
有一个角是直角的平行四边形是矩形。
你还有其它的判定方法吗?
ABCD
∠A=900
四边形ABCD是矩形
如果四边形ABCD的对角线AC=BD,这样的四边形是不是矩形?
A
B
C
D
AC=BD
A
B
C
D
AC=BD
都不是矩形
O
如果一个平行四边形的对角线变成相等呢?
A
B
C
D
将AC同时向两边拉长,使AC=BD
O
A
B
C
D
现在的
ABCD会是一个什么图形?
情境一:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形
。
命题:对角线相等的平行四边形是矩形。
已知:如图,在平行四边形ABCD中,AC=BD。求证:四边形ABCD是矩形。
A
B
C
D
证明:
∵四边形ABCD是平行四边形
∴
AB=CD,
AC=BD,又∵
BC=CB,
∴
△ABC≌
△DCB(SSS)
∵
AB//CD
∴
∠ABC+∠DCB=180°
∴
∠ABC=∠DCB=90°
又∵
四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴
∠ABC=∠DCB
对角线相等的平行四边形是矩形
。
矩形的判定方法:
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
A
B
C
D
O
有一个角是直角
有两个角是直角
的
四边形是矩形吗?
有三个角是直角
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
情境一:李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有三个角是直角的四边形是矩形
。
你能证明上述结论吗?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°求证:四边形ABCD是矩形。
A
B
C
D
∟
∟
∟
证明:∵
∠A=∠B=90°
∴
∠A+∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD是平行四边形
又∵
∠A=90°
∴四边形ABCD是矩形
命题:有三个角是直角的四边形是矩形
矩形的判定方法:
有三个角是直角的四边形是矩形
。
A
B
C
D
∵
∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形
。
有三个角是直角的四边形是矩形
。
方法1:
方法2:
方法3:
例1:如图,在平行四边形ABCD中,对角线AC,BD
相交于点O,且OA=OD,
∠OAD=50°,
求:
∠OAB的度数.
范例解析,当堂练习
解:∵四边形ABCD是平行四边形
又∵OA=OD
∴AC=BD
∴四边形ABCD是矩形
A
B
C
D
O
∴∠DAB=90°
又∠OAD=50°
∴
∠OAB=40°
练一练
:
ABCD中,AC,BD交于
点O,△ABO为正三角形,AB=4cm.
求平行四边形的面积.
A
B
C
D
O
4
例2:1.BD、BE分别是∠ABC与它的邻补角的平分线,AE⊥BE,AD⊥BD,
求证:四边形AEBD是矩形。
证明:∵
AE⊥BE,AD⊥BD
∴
∠E=90°,
∠D=90°
∵
BD,BE分别是∠ABC与它的邻补角∠CBP的平分线
∴∠1=
∠ABC,∠2=
∠ABP
∴
□
AEBD是矩形
C
B
A
D
E
P
∟
∟
⌒
⌒
1
2
∴
∠1+∠2=
(∠ABC+∠ABP)=
×180°=90°
即∠DBE=90°
练测促学:1、下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
A
B
D
C
H
E
F
G
∵四边形ABCD是平行四边形
∴∠DAB+∠ABC=180
°
2、如图,
ABCD四个内角的平分线围成四边形EFGH,猜想四边形EFGH的形状,并说明理由
证明:
同理:∠EFG=90°、∠FGH=90°
∴四边形EFGH是矩形
∵AE、BE分别平分∠DAB、∠ABC
∴∠EAB+∠EBA=90
°
即∠AEB=90°
∴∠HEF=90°
3、如图,平行四边形ABCD中,AB=
6,BC=
8,AC=
10
,
求证
:
四边形ABCD是矩形。
D
B
C
A
证明:
∵AB=6,BC=8,AC=10
∴AB2+BC2=62+82=100=102=AC2
∴
∠B=90°
又∵
四边形ABCD是平行四边形
∴
□
ABCD是矩形
拓展延伸:如图,在△ABC中,点0是AC边上的一个动点,过点0作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,
A
B
C
M
N
0
)
1
)
2
(
5
(
4
(
3
(
6
(1)求证:0E=0F
(2)当0运动到何处时,
四边形AECF为矩形?
说明理由
E
F
证明:∵CF平分∠ACD
∴∠1=∠2
又∵
MN∥BC
∴∠1=∠3
∴
∠2=∠3
∴OC=OF
同理可证:OC=OE
∴OE=OF
D
答:当点0为AC的中点时,
四边形AECF是矩形
理由:由(1)知0E=0F,
又AO=CO
∴四边形AECF是平行四边形
又∵EC平分∠ACB,FC平分∠ACD
∴∠2+∠4=90°即∠ECF=90°
∴四边形AECF是矩形
∠A=
∠B=
∠C=90°
ABCD
AC
=
BD
ABCD
∠A=90°
ABCD
是矩形
四边形ABCD
是矩形
谈一谈,今天你有何收获?
判定一个四边形是矩形的方法是:
本节课我们学习了什么内容,你能总结吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形
。
有三个角是直角的四边形是矩形
。
方法1:
方法2:
方法3:
P55
练习2题
P60
习题第1、2题
作业:
