2020-2021学年冀教版七年级数学下册第七章相交线与平行线单元检测卷(word版,含答案)
文档属性
| 名称 | 2020-2021学年冀教版七年级数学下册第七章相交线与平行线单元检测卷(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 468.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 17:05:31 | ||
图片预览



文档简介
2020-2021学年度冀教版七年级数学下册第七章相交线与平行线单元检测卷
一、单选题
1.下列句子中,属于命题的是(
)
①三角形的内角和等于180度;②对顶角相等;③过一点作已知直线的垂线;④两点确定一条直线.
A.①④
B.①②④
C.①②③
D.②③
2.如图,三条直线相交于点O,则∠1+∠2+∠3的度数等于(
)
A.210°
B.180°
C.150°
D.120°
3.下列说法正确的个数是
(
)
①同位角相等;
②过一点有且只有一条直线与已知直线垂直;
③过一点有且只有一条直线与已知直线平行;④三条直线两两相交,总有三个交点;⑤若a∥b,b∥c,则a∥c.
A.1个
B.2个
C.3个
D.4个
4.如图,下列不能判定的条件是(
)
A.
B.
C.
D.
5.如图,直线为直角,则等于(
)
A.
B.
C.
D.
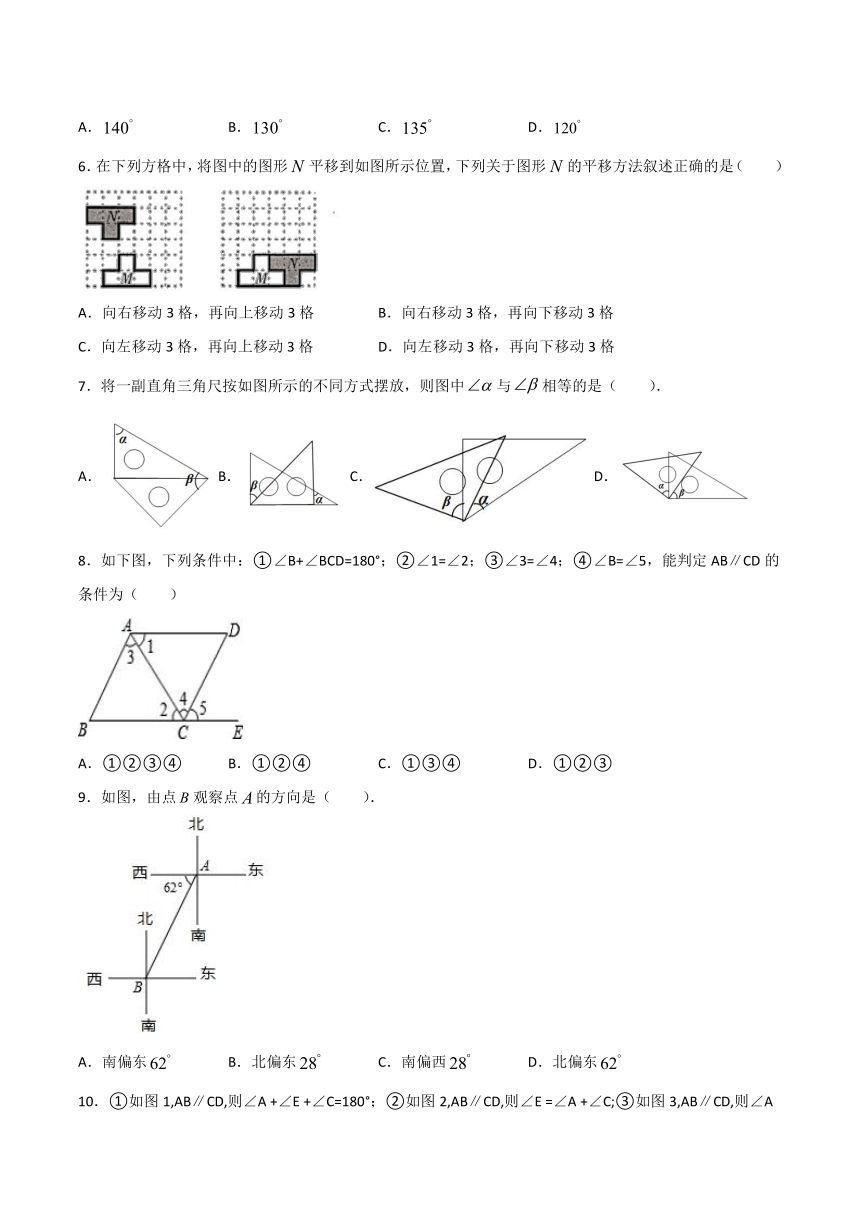
6.在下列方格中,将图中的图形平移到如图所示位置,下列关于图形的平移方法叙述正确的是(
)
A.向右移动3格,再向上移动3格
B.向右移动3格,再向下移动3格
C.向左移动3格,再向上移动3格
D.向左移动3格,再向下移动3格
7.将一副直角三角尺按如图所示的不同方式摆放,则图中与相等的是(
).
A.B.C.
D.
8.如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
A.①②③④
B.①②④
C.①③④
D.①②③
9.如图,由点观察点的方向是(
).
A.南偏东
B.北偏东
C.南偏西
D.北偏东
10.①如图1,AB∥CD,则∠A
+∠E
+∠C=180°;②如图2,AB∥CD,则∠E
=∠A
+∠C;③如图3,AB∥CD,则∠A
+∠E-∠1=180°
;
④如图4,AB∥CD,则∠A=∠C
+∠P.以上结论正确的个数是(
)
A.、1个
B.2个
C.3个
D.4个
二、填空题
11.给出下列说法:①同角的补角相等;②相等的角是对顶角;③两点确定一条直线;④过一点有且只有一条直线与已知直线平行,其中正确的有___个.
12.如图,直线AB、CD相交于点O,OE平分,,,则=_______.
13.如图,若,,则___________度.
14.如图,AB//CD,则图中_______________°;
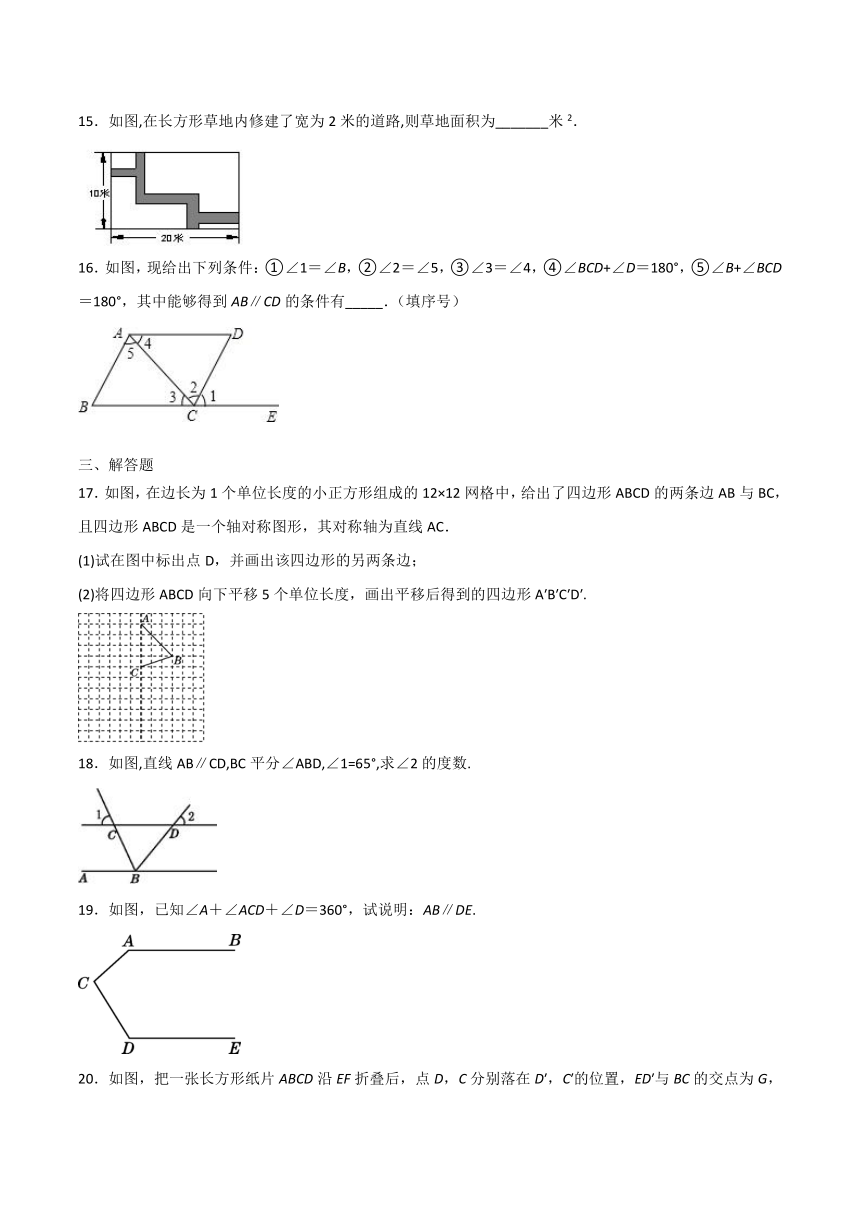
15.如图,在长方形草地内修建了宽为2米的道路,则草地面积为_______米2.
16.如图,现给出下列条件:①∠1=∠B,②∠2=∠5,③∠3=∠4,④∠BCD+∠D=180°,⑤∠B+∠BCD=180°,其中能够得到AB∥CD的条件有_____.(填序号)
三、解答题
17.如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
(1)试在图中标出点D,并画出该四边形的另两条边;
(2)将四边形ABCD向下平移5个单位长度,画出平移后得到的四边形A′B′C′D′.
18.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
19.如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.
20.如图,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′的位置,ED′与BC的交点为G,若∠EFG=55°,求∠1,∠2的度数.
21.如图,∠AGF=∠ABC,∠1+∠2=180°,
(1)求证;BF∥DE
(2)如果DE垂直于AC,∠2=150°,求∠AFG的度数.
22.先阅读所给材料再完成后面的问题:
如图①所示,AB∥CD,试说明∠B+∠D=∠BED.
解:过点E作EF∥CD,易知EF∥AB,所以∠DEF=∠D,∠FEB=∠B,所以∠BED=∠FEB+∠DEF=∠B+∠D.若图中点E的位置发生变化,如图②③④所示,则上面问题中的三个角(均小于180°)有何数量关系?写出结论,并选择图②说明理由.
23.已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
参考答案
1.B
解:
①三角形的内角和等于180°,是三角形内角和定理,是命题;
②对顶角相等,是对顶角的性质,是命题;
③过一点作已知直线的垂线,是作图,不是命题;
④两点确定一条直线,是直线的性质,是命题,
综上所述,属于命题是①②④.
2.B
解:如图,
∵∠4=∠3,
∴∠1+∠2+∠3=∠1+∠2+∠4=180°.
3.A
①同位角相等,错误,只有两直线平行,才有同位角相等;
②应为:在同一平面内,过一点有且只有一条直线与已知直线垂直,故本小题错误;
③应为:过直线外一点有且只有一条直线与已知直线平行,故本小题错误;
④三条直线两两相交,总有一个交点或三个交点,故本小题错误;
⑤若a∥b,b∥c,则a∥c,平行于同一直线的两条直线平行,正确.
综上所述,正确的只有⑤共1个.
4.C
解:A.与是同位角,由同位角相同可判断,故选项A正确,不符合题意;
B.
与是内错角,由内错角相等可判断,故选项B正确,不符合题意;
C.由可判断,不能判断,故此选项符合题意;
D.
,由同旁内角互补两直线平行可得,故选项D正确,不符合题意.
故选:C.
5.B
解:过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF.
∴∠C=∠FEC,∠BAE=∠FEA.
∵∠C=40°,∠AEC为直角,
∴∠FEC=40°,∠BAE=∠AEF=90°?40°=50°.
∴∠1=180°?∠BAE=180°?50°=130°.
6.B
根据图形可知,向右移动3格,再向下移动3格即可得到图形;
故选:B.
7.D
如下图
选项A中,,
∴与不相等,故选项A错误;
如下图
选项B中,,
∵
∴与不相等,故选项B错误;
如下图
选项C中,,
∴与不相等,故选项C错误;
如下图:
选项D中,,
∴与相等;
8.C
解:①∵∠B+∠BCD=180°,
∴AB∥CD;
②∵∠1=∠2,
∴AD∥BC;
③∵∠3=∠4,
∴AB∥CD;
④∵∠B=∠5,
∴AB∥CD;
∴能得到AB∥CD的条件是①③④.
9.B
解:如图所示:
∵东西方向是平行的,
∴∠ABE=∠DAB=
62°
,
∵∠CBE=90°,
∴∠CBA=90°-62°=28°,
即由点B观察点A的方向是北偏东28°,
10.C
①如图1,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A+∠AEF=180°,∠C+∠CEF=180°,
所以∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°,则①错误;
②如图2,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A=∠AEF,∠C=∠CEF,
所以∠A+∠C=∠AEC+∠AEF=∠AEC,则②正确;
③如图3,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A+∠AEF=180°,∠1=∠CEF,所以∠A+∠AEC-∠1=∠A+∠AEC-∠CEF=∠A+∠AEF=180°,则③正确;
④如图4,过点P作PF∥AB,因为AB∥CD,所以AB∥PF∥CD,
所以∠A=∠APF,∠C=∠CPF,所以∠A=∠CPF+∠APC=∠C+∠APC,则④正确;
故选C.
11.2
同角的补角相等,故①符合题意;
对顶角相等,但相等的角不一定是对顶角,故②不符合题意;
两点确定一条直线,故③符合题意;
过直线外一点有且只有一条直线与已知直线平行,故④不符合题意;
12.18°
解:∵OE平分,
∴∠BOD=
∵直线AB、CD相交于点O,
∴∠AOC=∠BOD=72°
∵
∴∠COF=90°
∴
13.145
解:,,
,
.
故答案为:145.
14.180
如图:过点E作EF//CD.
∴∠3=∠FEC
∵∠AEF+∠2=∠FEC,
∴∠2+∠AEF=∠3,
∴,
∵AB//CD,EF//CD,
∴EF//AB,
∴∠1+∠AEF=180°
∴.
15.144
解:由图形得到了的总长度为20+10-2=28米,
所以道路的总面积为28×2=56米2,
所以草地面积为20×10-56=144米2.
故答案为:144
16.①②⑤
解:①若∠1=∠B,根据同位角相等,两直线平行可得AB∥CD;
②若∠2=∠5,根据内错角相等,两直线平行可得AB∥CD;
③若∠3=∠4,根据内错角相等,两直线平行可得AD∥BC,但不能得出AB∥CD;
④若∠BCD+∠D=180°,根据同旁内角互补,两直线平行可得AD∥BC,但不能得出AB∥CD;
⑤若∠B+∠BCD=180°,根据同旁内角互补,两直线平行可得AB∥CD;
综上,能够得到AB∥CD的条件有①②⑤.
故答案为:①②⑤.
17.
(1)点D及四边形ABCD的另两条边如图所示.
(2)得到的四边形A′B′C′D′如图所示.
【点睛】
本题考查平移变换、轴对称的性质,解题的关键是理解轴对称的意义,图形的平移实际是点在平移.
18.50°.
试题分析:由平行线的性质得到∠ABC=∠1=65°,∠ABD+∠BDC=180°,由BC平分∠ABD,得到∠ABD=2∠ABC=130°,于是得到结论.
解:∵AB∥CD,
∴∠ABC=∠1=65°,
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°,
∴∠BDC=180°﹣∠ABD=50°,
∴∠2=∠BDC=50°.
19
过点C作CF∥AB.
∵CF∥AB,
∴∠A+∠ACF=180°.
∵∠A+∠ACD+∠D=360°,
∴∠D+∠FCD=180°,
∴CF∥DE,
∴AB∥DE.
20.70°,110°
由题意可知∠3=∠4=55°,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠2=∠3+∠4=110°,
∠1+∠2=180°,
∴∠1=70°.
21.
(1)BF∥DE,理由如下:
∵∠AGF=∠ABC,∴GF∥BC,∴∠1=∠3,
∵∠1+∠2=180°,∴∠3+∠2=180°,∴BF∥DE;
(2)∵BF∥DE,BF⊥AC,∴DE⊥AC,
∵∠1+∠2=180°,∠2=150°,∴∠1=30°,∴∠AFG=90°﹣30°=60°.
22.
图②中,∠BED+∠B=∠D.理由如下:
过点E作EF∥AB,如图所示.
易知∠BEF+∠B=180°.①
又因为AB∥CD,所以EF∥CD,所以∠DEF+∠D=180°.②
①-②,得∠BEF+∠B-∠DEF-∠D=180°-180°,
所以∠BED+∠B=∠D.
图③中,∠D-∠B=∠BED.图④中,∠BED+∠B+∠D=360°.
23.
(1)如图1,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)不成立
如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
试卷第1页,总3页
一、单选题
1.下列句子中,属于命题的是(
)
①三角形的内角和等于180度;②对顶角相等;③过一点作已知直线的垂线;④两点确定一条直线.
A.①④
B.①②④
C.①②③
D.②③
2.如图,三条直线相交于点O,则∠1+∠2+∠3的度数等于(
)
A.210°
B.180°
C.150°
D.120°
3.下列说法正确的个数是
(
)
①同位角相等;
②过一点有且只有一条直线与已知直线垂直;
③过一点有且只有一条直线与已知直线平行;④三条直线两两相交,总有三个交点;⑤若a∥b,b∥c,则a∥c.
A.1个
B.2个
C.3个
D.4个
4.如图,下列不能判定的条件是(
)
A.
B.
C.
D.
5.如图,直线为直角,则等于(
)
A.
B.
C.
D.
6.在下列方格中,将图中的图形平移到如图所示位置,下列关于图形的平移方法叙述正确的是(
)
A.向右移动3格,再向上移动3格
B.向右移动3格,再向下移动3格
C.向左移动3格,再向上移动3格
D.向左移动3格,再向下移动3格
7.将一副直角三角尺按如图所示的不同方式摆放,则图中与相等的是(
).
A.B.C.
D.
8.如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
A.①②③④
B.①②④
C.①③④
D.①②③
9.如图,由点观察点的方向是(
).
A.南偏东
B.北偏东
C.南偏西
D.北偏东
10.①如图1,AB∥CD,则∠A
+∠E
+∠C=180°;②如图2,AB∥CD,则∠E
=∠A
+∠C;③如图3,AB∥CD,则∠A
+∠E-∠1=180°
;
④如图4,AB∥CD,则∠A=∠C
+∠P.以上结论正确的个数是(
)
A.、1个
B.2个
C.3个
D.4个
二、填空题
11.给出下列说法:①同角的补角相等;②相等的角是对顶角;③两点确定一条直线;④过一点有且只有一条直线与已知直线平行,其中正确的有___个.
12.如图,直线AB、CD相交于点O,OE平分,,,则=_______.
13.如图,若,,则___________度.
14.如图,AB//CD,则图中_______________°;
15.如图,在长方形草地内修建了宽为2米的道路,则草地面积为_______米2.
16.如图,现给出下列条件:①∠1=∠B,②∠2=∠5,③∠3=∠4,④∠BCD+∠D=180°,⑤∠B+∠BCD=180°,其中能够得到AB∥CD的条件有_____.(填序号)
三、解答题
17.如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
(1)试在图中标出点D,并画出该四边形的另两条边;
(2)将四边形ABCD向下平移5个单位长度,画出平移后得到的四边形A′B′C′D′.
18.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
19.如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.
20.如图,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′的位置,ED′与BC的交点为G,若∠EFG=55°,求∠1,∠2的度数.
21.如图,∠AGF=∠ABC,∠1+∠2=180°,
(1)求证;BF∥DE
(2)如果DE垂直于AC,∠2=150°,求∠AFG的度数.
22.先阅读所给材料再完成后面的问题:
如图①所示,AB∥CD,试说明∠B+∠D=∠BED.
解:过点E作EF∥CD,易知EF∥AB,所以∠DEF=∠D,∠FEB=∠B,所以∠BED=∠FEB+∠DEF=∠B+∠D.若图中点E的位置发生变化,如图②③④所示,则上面问题中的三个角(均小于180°)有何数量关系?写出结论,并选择图②说明理由.
23.已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
参考答案
1.B
解:
①三角形的内角和等于180°,是三角形内角和定理,是命题;
②对顶角相等,是对顶角的性质,是命题;
③过一点作已知直线的垂线,是作图,不是命题;
④两点确定一条直线,是直线的性质,是命题,
综上所述,属于命题是①②④.
2.B
解:如图,
∵∠4=∠3,
∴∠1+∠2+∠3=∠1+∠2+∠4=180°.
3.A
①同位角相等,错误,只有两直线平行,才有同位角相等;
②应为:在同一平面内,过一点有且只有一条直线与已知直线垂直,故本小题错误;
③应为:过直线外一点有且只有一条直线与已知直线平行,故本小题错误;
④三条直线两两相交,总有一个交点或三个交点,故本小题错误;
⑤若a∥b,b∥c,则a∥c,平行于同一直线的两条直线平行,正确.
综上所述,正确的只有⑤共1个.
4.C
解:A.与是同位角,由同位角相同可判断,故选项A正确,不符合题意;
B.
与是内错角,由内错角相等可判断,故选项B正确,不符合题意;
C.由可判断,不能判断,故此选项符合题意;
D.
,由同旁内角互补两直线平行可得,故选项D正确,不符合题意.
故选:C.
5.B
解:过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF.
∴∠C=∠FEC,∠BAE=∠FEA.
∵∠C=40°,∠AEC为直角,
∴∠FEC=40°,∠BAE=∠AEF=90°?40°=50°.
∴∠1=180°?∠BAE=180°?50°=130°.
6.B
根据图形可知,向右移动3格,再向下移动3格即可得到图形;
故选:B.
7.D
如下图
选项A中,,
∴与不相等,故选项A错误;
如下图
选项B中,,
∵
∴与不相等,故选项B错误;
如下图
选项C中,,
∴与不相等,故选项C错误;
如下图:
选项D中,,
∴与相等;
8.C
解:①∵∠B+∠BCD=180°,
∴AB∥CD;
②∵∠1=∠2,
∴AD∥BC;
③∵∠3=∠4,
∴AB∥CD;
④∵∠B=∠5,
∴AB∥CD;
∴能得到AB∥CD的条件是①③④.
9.B
解:如图所示:
∵东西方向是平行的,
∴∠ABE=∠DAB=
62°
,
∵∠CBE=90°,
∴∠CBA=90°-62°=28°,
即由点B观察点A的方向是北偏东28°,
10.C
①如图1,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A+∠AEF=180°,∠C+∠CEF=180°,
所以∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°,则①错误;
②如图2,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A=∠AEF,∠C=∠CEF,
所以∠A+∠C=∠AEC+∠AEF=∠AEC,则②正确;
③如图3,过点E作EF∥AB,
因为AB∥CD,所以AB∥EF∥CD,
所以∠A+∠AEF=180°,∠1=∠CEF,所以∠A+∠AEC-∠1=∠A+∠AEC-∠CEF=∠A+∠AEF=180°,则③正确;
④如图4,过点P作PF∥AB,因为AB∥CD,所以AB∥PF∥CD,
所以∠A=∠APF,∠C=∠CPF,所以∠A=∠CPF+∠APC=∠C+∠APC,则④正确;
故选C.
11.2
同角的补角相等,故①符合题意;
对顶角相等,但相等的角不一定是对顶角,故②不符合题意;
两点确定一条直线,故③符合题意;
过直线外一点有且只有一条直线与已知直线平行,故④不符合题意;
12.18°
解:∵OE平分,
∴∠BOD=
∵直线AB、CD相交于点O,
∴∠AOC=∠BOD=72°
∵
∴∠COF=90°
∴
13.145
解:,,
,
.
故答案为:145.
14.180
如图:过点E作EF//CD.
∴∠3=∠FEC
∵∠AEF+∠2=∠FEC,
∴∠2+∠AEF=∠3,
∴,
∵AB//CD,EF//CD,
∴EF//AB,
∴∠1+∠AEF=180°
∴.
15.144
解:由图形得到了的总长度为20+10-2=28米,
所以道路的总面积为28×2=56米2,
所以草地面积为20×10-56=144米2.
故答案为:144
16.①②⑤
解:①若∠1=∠B,根据同位角相等,两直线平行可得AB∥CD;
②若∠2=∠5,根据内错角相等,两直线平行可得AB∥CD;
③若∠3=∠4,根据内错角相等,两直线平行可得AD∥BC,但不能得出AB∥CD;
④若∠BCD+∠D=180°,根据同旁内角互补,两直线平行可得AD∥BC,但不能得出AB∥CD;
⑤若∠B+∠BCD=180°,根据同旁内角互补,两直线平行可得AB∥CD;
综上,能够得到AB∥CD的条件有①②⑤.
故答案为:①②⑤.
17.
(1)点D及四边形ABCD的另两条边如图所示.
(2)得到的四边形A′B′C′D′如图所示.
【点睛】
本题考查平移变换、轴对称的性质,解题的关键是理解轴对称的意义,图形的平移实际是点在平移.
18.50°.
试题分析:由平行线的性质得到∠ABC=∠1=65°,∠ABD+∠BDC=180°,由BC平分∠ABD,得到∠ABD=2∠ABC=130°,于是得到结论.
解:∵AB∥CD,
∴∠ABC=∠1=65°,
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°,
∴∠BDC=180°﹣∠ABD=50°,
∴∠2=∠BDC=50°.
19
过点C作CF∥AB.
∵CF∥AB,
∴∠A+∠ACF=180°.
∵∠A+∠ACD+∠D=360°,
∴∠D+∠FCD=180°,
∴CF∥DE,
∴AB∥DE.
20.70°,110°
由题意可知∠3=∠4=55°,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠2=∠3+∠4=110°,
∠1+∠2=180°,
∴∠1=70°.
21.
(1)BF∥DE,理由如下:
∵∠AGF=∠ABC,∴GF∥BC,∴∠1=∠3,
∵∠1+∠2=180°,∴∠3+∠2=180°,∴BF∥DE;
(2)∵BF∥DE,BF⊥AC,∴DE⊥AC,
∵∠1+∠2=180°,∠2=150°,∴∠1=30°,∴∠AFG=90°﹣30°=60°.
22.
图②中,∠BED+∠B=∠D.理由如下:
过点E作EF∥AB,如图所示.
易知∠BEF+∠B=180°.①
又因为AB∥CD,所以EF∥CD,所以∠DEF+∠D=180°.②
①-②,得∠BEF+∠B-∠DEF-∠D=180°-180°,
所以∠BED+∠B=∠D.
图③中,∠D-∠B=∠BED.图④中,∠BED+∠B+∠D=360°.
23.
(1)如图1,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)不成立
如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
试卷第1页,总3页
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
