2020-2021学年九年级数学人教版下册:28.1 锐角三角函数 教案
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册:28.1 锐角三角函数 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 135.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 17:29:59 | ||
图片预览


文档简介
课
题:
锐角三角函数第1课时
一、教学目标
知识与技能
初步了解锐角三角函数的意义,初步理解在直角三角形中一个锐角的对边与斜边的比值就是这个锐角的正弦的定义,并会根据已知直角三角形的边长求一个锐角的正弦值。
过程与方法
从实际问题入手研究,经历从发现到解决直角三角形中的一个锐角所对应的对边与斜边之间的关系的过程,体会研究数学问题的一般方法以及所采用的思考问题的方法。
情感态度与价值观
在解决问题的过程中体验求索的科学精神以及严谨的科学态度,进一步激发学习需求。
二、教学重难点
重点
锐角的正弦的定义
难点
理解直角三角形中一个锐角与其对边与斜边比值的对应关系。
三、教学过程设计
课题:锐角三角函数
问题与情境
师生行为
设计意图
活动1
创设情境,引入课题始建于1173年的意大利比萨斜塔因其“斜而未倒”成为世界建筑史上的奇迹,据说科学家伽利略曾在斜塔上做过自由落体运动实验,你能用“塔身中心线偏离垂直中心线的角度”来描述比萨斜塔的倾斜程度吗?此问题涉及锐角三角函数的知识,只要你认真学习本章,相信你能行!活动2
动手动脑,感知规律
问题
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?如果出水口的高度为50米,那需要准备多长的水管呢?活动3合作交流
达成共识
一般地,当A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?如下
图:RTABC与
RT
A1B1C1,∠C=∠C1=900
,
∠A=∠A1=a
,
那么与有什么关系?这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.活动4
确立课题如图,在RTABC
中,∠C=900
,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作sinA.
即
提问:∠B的正弦怎么表示?要求一个锐角的正弦值,我们需要知道直角三角形中的那些边?活动5巩固新知
消化新知例1、如图:在RTABC中,
∠C=900
,求sinA和sinB
的值
活动6
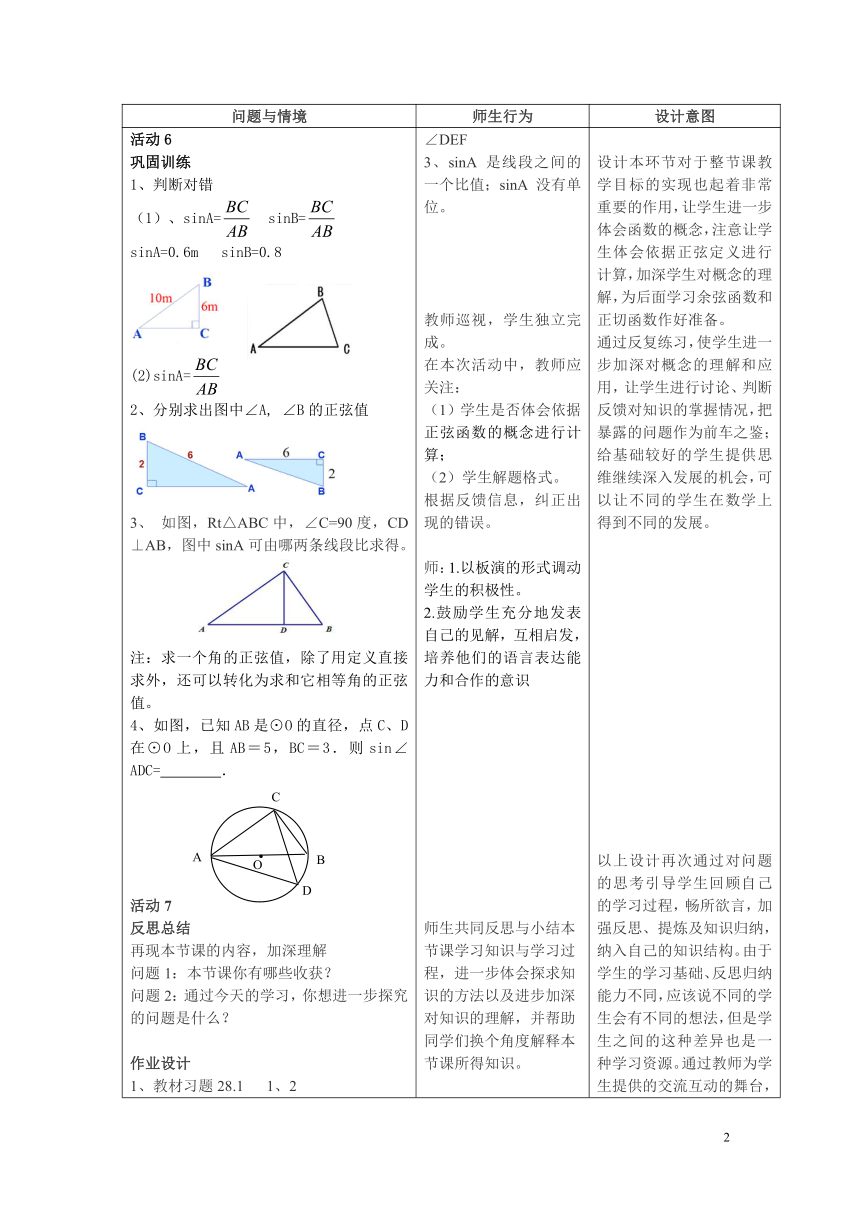
巩固训练1、判断对错(1)、sinA=
sinB=sinA=0.6m
sinB=0.8(2)sinA=2、分别求出图中∠A,
∠B的正弦值3、
如图,Rt△ABC中,∠C=90度,CD⊥AB,图中sinA可由哪两条线段比求得。注:求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。4、如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=5,BC=3.则sin∠ADC=
.活动7反思总结再现本节课的内容,加深理解问题1:本节课你有哪些收获?问题2:通过今天的学习,你想进一步探究的问题是什么?作业设计1、教材习题28.1
1、2
师生共同研究这个问题的知识背景是什么?共同探讨形成这个问题的条件是什么?师:你是运用以前所学过的什么知识解决的呢?生:30°直角三角形中,30°角所对的直角边等于斜边的一半。可以用小组学习的形式(按四人一组),每个学生有自己的分工,各负其责。从中引导学生发现:直角三角形中,锐角大小确定后,这个角的对边与斜边的比值随之确定。教师用几何画板展示成果。学生用相似三角形来论证。解决这个问题时,发现相似形的问题实质上是角确定而决定的,当角不变时,相似三角形的比值相对不变的现象提供一个重要的依据.师:强调“在直角三角形中,当锐角的度数固定时,它的对边与斜边的比也就固定下来”对于每一个锐角,都有这样的一个比值与之对应,从而可以合理的诠释正弦函数的概念,进一步体会到锐角与比值之间的一一对应关系。师:注意:1、sinA不是
sin与A的乘积,而是一个整体;2、正弦的三种表示方式:sinA、sin56°、sin∠DEF3、sinA
是线段之间的一个比值;sinA
没有单位。教师巡视,学生独立完成。在本次活动中,教师应关注:(1)学生是否体会依据正弦函数的概念进行计算;(2)学生解题格式。根据反馈信息,纠正出现的错误。师:1.以板演的形式调动学生的积极性。2.鼓励学生充分地发表自己的见解,互相启发,培养他们的语言表达能力和合作的意识师生共同反思与小结本节课学习知识与学习过程,进一步体会探求知识的方法以及进步加深对知识的理解,并帮助同学们换个角度解释本节课所得知识。作业由学生回家独立完成。
以测量比萨斜塔的倾斜程度创设情境引出课题,目的是让学生开阔视野并使学生感受到“数学问题来源于生活,同时又服务于生活”的真谛,根据问题情境中的数据,我们无法用已有的知识和方法解决这个实际问题,但学习本章之后就可以解决了,这样可以引起学生的好奇心,激发学生的学习兴趣。联系生活实际,利用生动的语言和形象的画面创设问题情境,促使学生去猜想、去探索、去发现,激发求知欲。让学生进一步体会数学知识无处不在,这样更加增强了学生学数学、用数学的信心。鼓励学生运用自己的方法解决问题,适时点拨,有的学生可能运用解数值解决问题,有的学生可能靠逻辑推理解决问题,无论论哪种方法教师都应给予肯定,以调动学生学习的积极性;鼓励学生为完成共同的目标,进行交流互动性的学习,引导学生倾听他人的意见,从交流中获益;学生在探索中体会由特殊到一般的过渡,给学生足够的时间讨论、思考、探索,有更多的机会体验到,在直角三角形中,当锐角的度数一定时,这个锐角的对边与斜边的比值就是一个固定值,这为认识正弦函数的概念铺设了必要的台阶,从而水到渠成地给出正弦函数的概念。安排这道题目的目的是让学生体会正弦函数的概念,为学生提供自主探究的空间,学生既能独立思考,又能互相合作。设计本环节对于整节课教学目标的实现也起着非常重要的作用,让学生进一步体会函数的概念,注意让学生体会依据正弦定义进行计算,加深学生对概念的理解,为后面学习余弦函数和正切函数作好准备。通过反复练习,使学生进一步加深对概念的理解和应用,让学生进行讨论、判断反馈对知识的掌握情况,把暴露的问题作为前车之鉴;给基础较好的学生提供思维继续深入发展的机会,可以让不同的学生在数学上得到不同的发展。以上设计再次通过对问题的思考引导学生回顾自己的学习过程,畅所欲言,加强反思、提炼及知识归纳,纳入自己的知识结构。由于学生的学习基础、反思归纳能力不同,应该说不同的学生会有不同的想法,但是学生之间的这种差异也是一种学习资源。通过教师为学生提供的交流互动的舞台,使学生在倾听别人的想法、意见、收获的同时,不断完善自己的认识。
板书设计
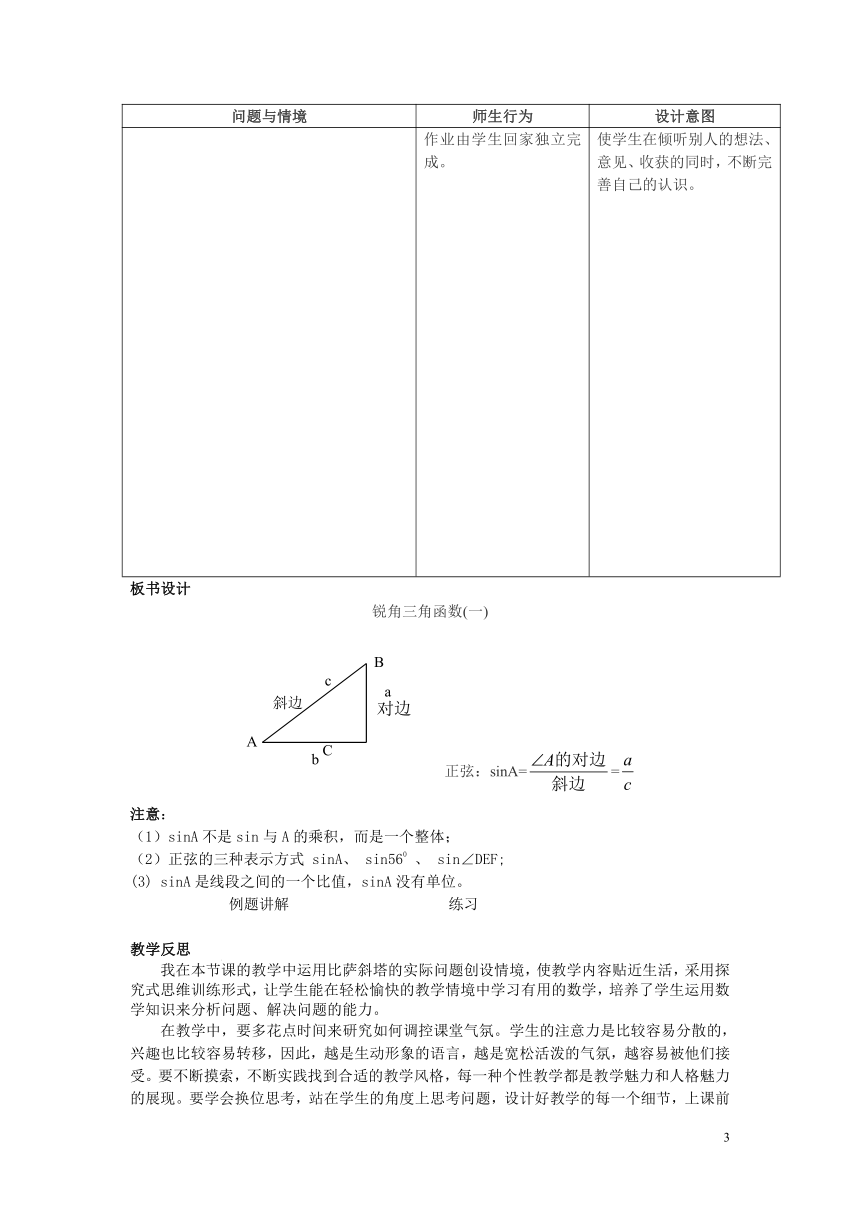
锐角三角函数(一)
正弦:sinA==
注意:
(1)sinA不是sin与A的乘积,而是一个整体;
(2)正弦的三种表示方式
sinA、
sin560
、
sin∠DEF;
(3)
sinA是线段之间的一个比值,sinA没有单位。
例题讲解
练习
教学反思
我在本节课的教学中运用比萨斜塔的实际问题创设情境,使教学内容贴近生活,采用探究式思维训练形式,让学生能在轻松愉快的教学情境中学习有用的数学,培养了学生运用数学知识来分析问题、解决问题的能力。
在教学中,要多花点时间来研究如何调控课堂气氛。学生的注意力是比较容易分散的,兴趣也比较容易转移,因此,越是生动形象的语言,越是宽松活泼的气氛,越容易被他们接受。要不断摸索,不断实践找到合适的教学风格,每一种个性教学都是教学魅力和人格魅力的展现。要学会换位思考,站在学生的角度上思考问题,设计好教学的每一个细节,上课前多揣摩。让学生更多地参与到课堂的教学过程中,让学生体验思考的过程,体验成功的喜悦和失败的挫折,学会真正把课堂还给学生,让学生来做课堂的主角。
28.1锐角三角函数第2课时
一.教学目标:
知识与技能:了解锐角三角函数的概念,能够正确应用sinA、cosA、tanA表示直角三角形中两边的比。
过程与方法:通过锐角三角函数的学习,进一步认识函数,体会函数的变化与对应的思想,逐步培养学生会观察、比较、分析、概括等逻辑思维能力。
情感态度与价值观:引导学生探索、发现,以培养学生独立思考、勇于创新的精神和良好的学习习惯。
二.课时分配:1课时
三.教学重点与难点:
重点:理解余弦、正切的概念。
难点:熟练运用锐角三角函数的概念进行有关计算。
四.教学方法与学习方式:
教学方法:启发式教学法
学习方式:自主、合作探究学习方式
五.教学过程:
(一)复习提问:正弦的定义:在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的
正弦。记作sinA,即sinA=a/c
(2)自学汇报:探究一
如图,在Rt△ABC中,∠C=90°当∠A确定时,∠A的对边与斜边的比就确定,此时,其他边之间的比是否也确定呢?
(三)自主探究:
余弦:在Rt△ABC中,∠C=90°,我们把锐角A的邻边与斜边的比叫做∠A的余弦。记作cosA,即cosA=b/c
正切:在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切。记作tanA,即tanA=a/b
(四)展示交流:
例1
如图,在Rt△ABC中,∠C=90°,BC=6,sinA=
3/5
,求cosA、tanA的值。
例2.已知锐角α的始边在x轴的正半轴上(顶点在原点),终边上一点的坐标为(1,2),求角α的三个三角函数值。
三角函数的定义:
锐角A的正弦、余弦、正切统称为
锐角三角函数。
所以,对于任何一个锐角α
,有
0<sinα<1,
0<cosα<1,
tanα
>0,
(5)实践检测:
1.如果α是锐角,且cosα=
3/5
,那么sin(90°-α)的值等于
2.直角三角形的斜边和一条直角边的比为25∶24,则其中最小的角的正切值为
。
(六)心灵感悟:
我想对你说……(自己、同伴、老师)
?
O
A
B
C
D
·
C
A
斜边
对边
c
b
a
B
x
o
y
PAGE
1
题:
锐角三角函数第1课时
一、教学目标
知识与技能
初步了解锐角三角函数的意义,初步理解在直角三角形中一个锐角的对边与斜边的比值就是这个锐角的正弦的定义,并会根据已知直角三角形的边长求一个锐角的正弦值。
过程与方法
从实际问题入手研究,经历从发现到解决直角三角形中的一个锐角所对应的对边与斜边之间的关系的过程,体会研究数学问题的一般方法以及所采用的思考问题的方法。
情感态度与价值观
在解决问题的过程中体验求索的科学精神以及严谨的科学态度,进一步激发学习需求。
二、教学重难点
重点
锐角的正弦的定义
难点
理解直角三角形中一个锐角与其对边与斜边比值的对应关系。
三、教学过程设计
课题:锐角三角函数
问题与情境
师生行为
设计意图
活动1
创设情境,引入课题始建于1173年的意大利比萨斜塔因其“斜而未倒”成为世界建筑史上的奇迹,据说科学家伽利略曾在斜塔上做过自由落体运动实验,你能用“塔身中心线偏离垂直中心线的角度”来描述比萨斜塔的倾斜程度吗?此问题涉及锐角三角函数的知识,只要你认真学习本章,相信你能行!活动2
动手动脑,感知规律
问题
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?如果出水口的高度为50米,那需要准备多长的水管呢?活动3合作交流
达成共识
一般地,当A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?如下
图:RTABC与
RT
A1B1C1,∠C=∠C1=900
,
∠A=∠A1=a
,
那么与有什么关系?这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.活动4
确立课题如图,在RTABC
中,∠C=900
,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作sinA.
即
提问:∠B的正弦怎么表示?要求一个锐角的正弦值,我们需要知道直角三角形中的那些边?活动5巩固新知
消化新知例1、如图:在RTABC中,
∠C=900
,求sinA和sinB
的值
活动6
巩固训练1、判断对错(1)、sinA=
sinB=sinA=0.6m
sinB=0.8(2)sinA=2、分别求出图中∠A,
∠B的正弦值3、
如图,Rt△ABC中,∠C=90度,CD⊥AB,图中sinA可由哪两条线段比求得。注:求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。4、如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=5,BC=3.则sin∠ADC=
.活动7反思总结再现本节课的内容,加深理解问题1:本节课你有哪些收获?问题2:通过今天的学习,你想进一步探究的问题是什么?作业设计1、教材习题28.1
1、2
师生共同研究这个问题的知识背景是什么?共同探讨形成这个问题的条件是什么?师:你是运用以前所学过的什么知识解决的呢?生:30°直角三角形中,30°角所对的直角边等于斜边的一半。可以用小组学习的形式(按四人一组),每个学生有自己的分工,各负其责。从中引导学生发现:直角三角形中,锐角大小确定后,这个角的对边与斜边的比值随之确定。教师用几何画板展示成果。学生用相似三角形来论证。解决这个问题时,发现相似形的问题实质上是角确定而决定的,当角不变时,相似三角形的比值相对不变的现象提供一个重要的依据.师:强调“在直角三角形中,当锐角的度数固定时,它的对边与斜边的比也就固定下来”对于每一个锐角,都有这样的一个比值与之对应,从而可以合理的诠释正弦函数的概念,进一步体会到锐角与比值之间的一一对应关系。师:注意:1、sinA不是
sin与A的乘积,而是一个整体;2、正弦的三种表示方式:sinA、sin56°、sin∠DEF3、sinA
是线段之间的一个比值;sinA
没有单位。教师巡视,学生独立完成。在本次活动中,教师应关注:(1)学生是否体会依据正弦函数的概念进行计算;(2)学生解题格式。根据反馈信息,纠正出现的错误。师:1.以板演的形式调动学生的积极性。2.鼓励学生充分地发表自己的见解,互相启发,培养他们的语言表达能力和合作的意识师生共同反思与小结本节课学习知识与学习过程,进一步体会探求知识的方法以及进步加深对知识的理解,并帮助同学们换个角度解释本节课所得知识。作业由学生回家独立完成。
以测量比萨斜塔的倾斜程度创设情境引出课题,目的是让学生开阔视野并使学生感受到“数学问题来源于生活,同时又服务于生活”的真谛,根据问题情境中的数据,我们无法用已有的知识和方法解决这个实际问题,但学习本章之后就可以解决了,这样可以引起学生的好奇心,激发学生的学习兴趣。联系生活实际,利用生动的语言和形象的画面创设问题情境,促使学生去猜想、去探索、去发现,激发求知欲。让学生进一步体会数学知识无处不在,这样更加增强了学生学数学、用数学的信心。鼓励学生运用自己的方法解决问题,适时点拨,有的学生可能运用解数值解决问题,有的学生可能靠逻辑推理解决问题,无论论哪种方法教师都应给予肯定,以调动学生学习的积极性;鼓励学生为完成共同的目标,进行交流互动性的学习,引导学生倾听他人的意见,从交流中获益;学生在探索中体会由特殊到一般的过渡,给学生足够的时间讨论、思考、探索,有更多的机会体验到,在直角三角形中,当锐角的度数一定时,这个锐角的对边与斜边的比值就是一个固定值,这为认识正弦函数的概念铺设了必要的台阶,从而水到渠成地给出正弦函数的概念。安排这道题目的目的是让学生体会正弦函数的概念,为学生提供自主探究的空间,学生既能独立思考,又能互相合作。设计本环节对于整节课教学目标的实现也起着非常重要的作用,让学生进一步体会函数的概念,注意让学生体会依据正弦定义进行计算,加深学生对概念的理解,为后面学习余弦函数和正切函数作好准备。通过反复练习,使学生进一步加深对概念的理解和应用,让学生进行讨论、判断反馈对知识的掌握情况,把暴露的问题作为前车之鉴;给基础较好的学生提供思维继续深入发展的机会,可以让不同的学生在数学上得到不同的发展。以上设计再次通过对问题的思考引导学生回顾自己的学习过程,畅所欲言,加强反思、提炼及知识归纳,纳入自己的知识结构。由于学生的学习基础、反思归纳能力不同,应该说不同的学生会有不同的想法,但是学生之间的这种差异也是一种学习资源。通过教师为学生提供的交流互动的舞台,使学生在倾听别人的想法、意见、收获的同时,不断完善自己的认识。
板书设计
锐角三角函数(一)
正弦:sinA==
注意:
(1)sinA不是sin与A的乘积,而是一个整体;
(2)正弦的三种表示方式
sinA、
sin560
、
sin∠DEF;
(3)
sinA是线段之间的一个比值,sinA没有单位。
例题讲解
练习
教学反思
我在本节课的教学中运用比萨斜塔的实际问题创设情境,使教学内容贴近生活,采用探究式思维训练形式,让学生能在轻松愉快的教学情境中学习有用的数学,培养了学生运用数学知识来分析问题、解决问题的能力。
在教学中,要多花点时间来研究如何调控课堂气氛。学生的注意力是比较容易分散的,兴趣也比较容易转移,因此,越是生动形象的语言,越是宽松活泼的气氛,越容易被他们接受。要不断摸索,不断实践找到合适的教学风格,每一种个性教学都是教学魅力和人格魅力的展现。要学会换位思考,站在学生的角度上思考问题,设计好教学的每一个细节,上课前多揣摩。让学生更多地参与到课堂的教学过程中,让学生体验思考的过程,体验成功的喜悦和失败的挫折,学会真正把课堂还给学生,让学生来做课堂的主角。
28.1锐角三角函数第2课时
一.教学目标:
知识与技能:了解锐角三角函数的概念,能够正确应用sinA、cosA、tanA表示直角三角形中两边的比。
过程与方法:通过锐角三角函数的学习,进一步认识函数,体会函数的变化与对应的思想,逐步培养学生会观察、比较、分析、概括等逻辑思维能力。
情感态度与价值观:引导学生探索、发现,以培养学生独立思考、勇于创新的精神和良好的学习习惯。
二.课时分配:1课时
三.教学重点与难点:
重点:理解余弦、正切的概念。
难点:熟练运用锐角三角函数的概念进行有关计算。
四.教学方法与学习方式:
教学方法:启发式教学法
学习方式:自主、合作探究学习方式
五.教学过程:
(一)复习提问:正弦的定义:在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的
正弦。记作sinA,即sinA=a/c
(2)自学汇报:探究一
如图,在Rt△ABC中,∠C=90°当∠A确定时,∠A的对边与斜边的比就确定,此时,其他边之间的比是否也确定呢?
(三)自主探究:
余弦:在Rt△ABC中,∠C=90°,我们把锐角A的邻边与斜边的比叫做∠A的余弦。记作cosA,即cosA=b/c
正切:在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切。记作tanA,即tanA=a/b
(四)展示交流:
例1
如图,在Rt△ABC中,∠C=90°,BC=6,sinA=
3/5
,求cosA、tanA的值。
例2.已知锐角α的始边在x轴的正半轴上(顶点在原点),终边上一点的坐标为(1,2),求角α的三个三角函数值。
三角函数的定义:
锐角A的正弦、余弦、正切统称为
锐角三角函数。
所以,对于任何一个锐角α
,有
0<sinα<1,
0<cosα<1,
tanα
>0,
(5)实践检测:
1.如果α是锐角,且cosα=
3/5
,那么sin(90°-α)的值等于
2.直角三角形的斜边和一条直角边的比为25∶24,则其中最小的角的正切值为
。
(六)心灵感悟:
我想对你说……(自己、同伴、老师)
?
O
A
B
C
D
·
C
A
斜边
对边
c
b
a
B
x
o
y
PAGE
1
