8.4机械能守恒定律(共22张ppt)
文档属性
| 名称 | 8.4机械能守恒定律(共22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-30 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
横县百合完全中学——韦衍虎
8.4机械能守恒定律
问题导入
伽利略曾研究过小球在斜面上的运动。他发现:无论斜面B比斜面A陡些或缓些,小球的速度最后总会在斜面上的某点变为0,这点距斜面底端的竖直高度与它出发时的高度基本相同。
在小球的运动过程中,有哪些物理量是变化的?哪些是不变的?你能找出不变的量吗?
A
B
h
h
高度、质量
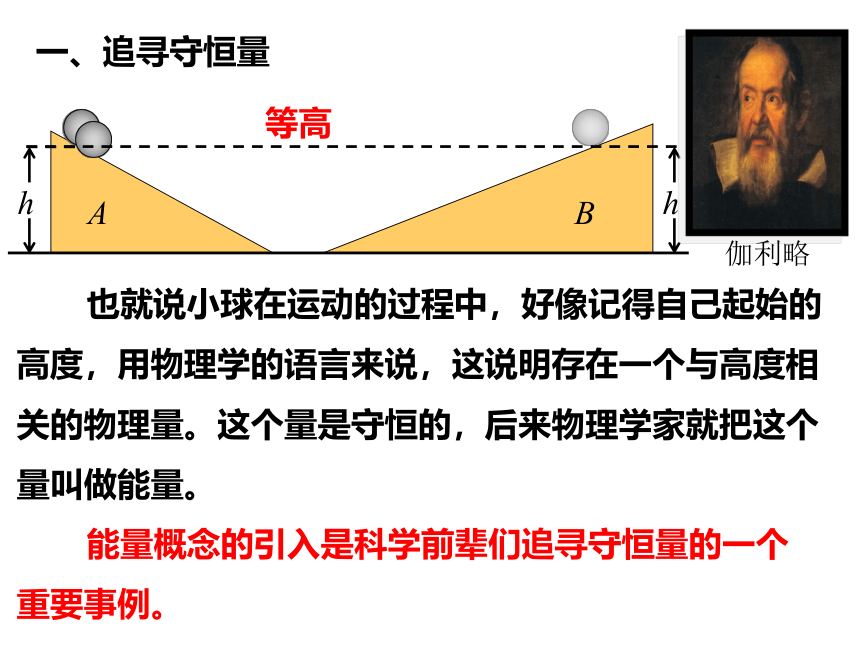
一、追寻守恒量
A
B
h
h
等高
伽利略
也就说小球在运动的过程中,好像记得自己起始的高度,用物理学的语言来说,这说明存在一个与高度相关的物理量。这个量是守恒的,后来物理学家就把这个量叫做能量。
能量概念的引入是科学前辈们追寻守恒量的一个重要事例。
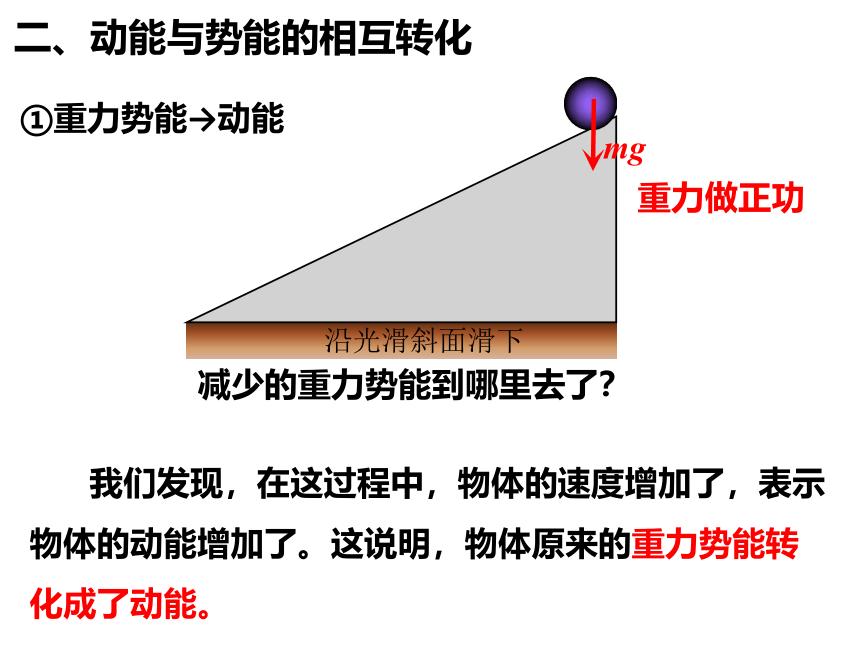
二、动能与势能的相互转化
mg
我们发现,在这过程中,物体的速度增加了,表示物体的动能增加了。这说明,物体原来的重力势能转化成了动能。
重力做正功
①重力势能→动能
减少的重力势能到哪里去了?
沿光滑斜面滑下
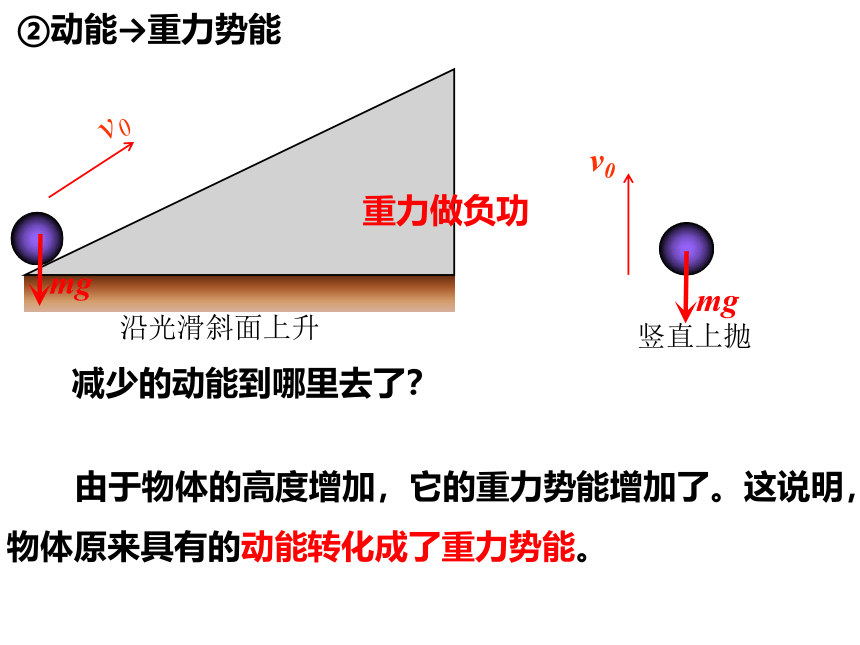
沿光滑斜面上升
mg
由于物体的高度增加,它的重力势能增加了。这说明,物体原来具有的动能转化成了重力势能。
v0
②动能→重力势能
重力做负功
减少的动能到哪里去了?
mg
竖直上抛
v0
③动能?弹性势能
被压缩的弹簧弹射的过程
弹性势能→动能
跳板上弹起的过程
弹性势能→动能
反之成立
机械能E
机械能=
动能+势能
从上面的讨论可以看出来,重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
重力势能
弹性势能
势能Ep重
动能Ek
势能Ep弹
重力做的功相等吗?重力势能的变化相等吗?动能的变化相等吗?重力势能各转化成什么形式的能?
①重力做功:WG=mgh
两小球的重力mg都是一样
,h=h1-h2也一样。
②重力做功=重力势能的变化:
WG=Ep1-Ep2
③合力做的功=动能的变化:
W=Ek2-Ek1
mg
mg
f阻
也可由合力做功的不同来判断
都是静止开始下落:Ek1=0
v2真>v2油,即Ek2真>Ek2油
重力做的功相等吗?重力势能的变化相等吗?动能的变化相等吗?重力势能各转化成什么形式的能?
mg
mg
f阻
④真空:重力势能→动能
油:重力势能→动能+内能
真空:只有重力做功。
油:除重力做功外还有阻力做功。
三、机械能守恒定律
物体在某一时刻处在高度为h1的位置A,这时它的速度是v1。经过一段时间后,物体下落到高度为h2的另一位置B,这时它的速度是v2。
只有重力做功
v
mg
FN
重力做功=重力势能的变化:
合力做的功=动能的变化:
初状态
末状态
在只有重力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
初状态A
=
末状态B
势能
动能
势能
动能
mgh1
mgh2
在图8.4-3中,如果物体从位置B沿光滑曲面上升到位置A,重力做负功。这种情况下上式的关系是否还成立?
初状态B
=
末状态A
势能
动能
势能
动能
mgh1
mgh2
等式两边相加得:
忽略阻力,只有重力做功
只有弹力做功的系统内
在只有重力或弹簧弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。
表达式:
守恒条件
只有系统内动能和势能相互转化,无其他形式能量之间(如内能)的转化。
只受重力或弹力,不受其它力。
常见的机械能守恒的例子:
①自由落体运动
②平抛运动(抛体)
③单摆(秋千)
④在光滑斜面上滑动的物体。
①从能量的观点看:
②从力的观点看:
课堂练习
例1:在下面列举的各个实例中(除A外都不
计空气阻力),哪些过程中机械能是守恒的?
说明理由
A.跳伞运动员带着张开的降落伞在空气中匀速下落
B.抛出的标枪在空中运动
C.拉着一个金属块使它沿光滑的斜面匀速上升
D、在光滑水平面上运动的小球碰到一个弹簧,把弹簧压缩后,又被弹回来
抓住只有重力或弹力做功的条件。
f阻做功
拉力做功
BD
课本例题:把一个小球用细绳悬挂起来,就成为一个摆,摆长为l,最大偏角为θ。小球运动到最低位置时的速度是多大?
T
mg
v
初状态A
=
末状态O
势能
动能
势能
动能
0
mgh
解:
0
lcosθ
h=l-lcosθ
用机械能守恒定律求解
左边相加等于右边相加:
W
=
Ek2
—
Ek1
0
重力做正功:mgh
解:
以小球为研究对象,运用动能定理。
左边相加等于右边:
h=l-lcosθ
满足机械能守恒的条件,只需考虑运动的初状态和末状态,不必考虑两个状态间过程的细节。
初状态的θ角越大,cosθ越小,(1
-
cosθ)就越大,v也就越大。也就是说,最初把小球拉得越高,它到达最低点时的速度也就越大。
初状态
=
末状态
势能
动能
势能
动能
课堂练习
质量为m的小球从光滑曲面上滑下。当它到达高度为h1的位置A时,速度的大小为v1,滑到高度为h2的位置B时,速度的大小为v2。在由高度h1滑到高度h2的过程中,重力做的功为W。
(1)根据动能定理列出方程,描述小球在A、B两点间动能的关系。
mg
FN
,支持力不做功,只有重力做功。
解:受力分析
W
=
Ek2
—
Ek1
mgh
左边相加等于右边:
h=h1-h2
(2)
根据重力做功与重力势能的关系,把以上方程变形,以反映出小球运动过程中机械能是守恒的。
h=h1-h2
初状态
=
末状态
势能
动能
势能
动能
解:以山脚为0势能面
mgh1
mgh2
左边相加等于右边相加:
一、动能与势能的相互转化
机械能=
动能+势能
重力势能、弹性势能与动能之间可以相互转化,我们把它们统称为机械能。
二、机械能守恒定律
在只有重力或弹簧弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。
E机2=E机1
表达式:
课堂小结
重力势能
弹性势能
守恒条件
只有系统内动能和势能相互转化,无其他形式能量之间(如内能)的转化。
只受重力或弹力,不受其它力。
常见的机械能守恒的例子:
①自由落体运动
②平抛运动(抛体)
③单摆(秋千)
④在光滑斜面上滑动的物体。
①从能量的观点看:
②从力的观点看:
横县百合完全中学——韦衍虎
8.4机械能守恒定律
问题导入
伽利略曾研究过小球在斜面上的运动。他发现:无论斜面B比斜面A陡些或缓些,小球的速度最后总会在斜面上的某点变为0,这点距斜面底端的竖直高度与它出发时的高度基本相同。
在小球的运动过程中,有哪些物理量是变化的?哪些是不变的?你能找出不变的量吗?
A
B
h
h
高度、质量
一、追寻守恒量
A
B
h
h
等高
伽利略
也就说小球在运动的过程中,好像记得自己起始的高度,用物理学的语言来说,这说明存在一个与高度相关的物理量。这个量是守恒的,后来物理学家就把这个量叫做能量。
能量概念的引入是科学前辈们追寻守恒量的一个重要事例。
二、动能与势能的相互转化
mg
我们发现,在这过程中,物体的速度增加了,表示物体的动能增加了。这说明,物体原来的重力势能转化成了动能。
重力做正功
①重力势能→动能
减少的重力势能到哪里去了?
沿光滑斜面滑下
沿光滑斜面上升
mg
由于物体的高度增加,它的重力势能增加了。这说明,物体原来具有的动能转化成了重力势能。
v0
②动能→重力势能
重力做负功
减少的动能到哪里去了?
mg
竖直上抛
v0
③动能?弹性势能
被压缩的弹簧弹射的过程
弹性势能→动能
跳板上弹起的过程
弹性势能→动能
反之成立
机械能E
机械能=
动能+势能
从上面的讨论可以看出来,重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
重力势能
弹性势能
势能Ep重
动能Ek
势能Ep弹
重力做的功相等吗?重力势能的变化相等吗?动能的变化相等吗?重力势能各转化成什么形式的能?
①重力做功:WG=mgh
两小球的重力mg都是一样
,h=h1-h2也一样。
②重力做功=重力势能的变化:
WG=Ep1-Ep2
③合力做的功=动能的变化:
W=Ek2-Ek1
mg
mg
f阻
也可由合力做功的不同来判断
都是静止开始下落:Ek1=0
v2真>v2油,即Ek2真>Ek2油
重力做的功相等吗?重力势能的变化相等吗?动能的变化相等吗?重力势能各转化成什么形式的能?
mg
mg
f阻
④真空:重力势能→动能
油:重力势能→动能+内能
真空:只有重力做功。
油:除重力做功外还有阻力做功。
三、机械能守恒定律
物体在某一时刻处在高度为h1的位置A,这时它的速度是v1。经过一段时间后,物体下落到高度为h2的另一位置B,这时它的速度是v2。
只有重力做功
v
mg
FN
重力做功=重力势能的变化:
合力做的功=动能的变化:
初状态
末状态
在只有重力做功的系统内,动能与重力势能互相转化时总的机械能保持不变。
初状态A
=
末状态B
势能
动能
势能
动能
mgh1
mgh2
在图8.4-3中,如果物体从位置B沿光滑曲面上升到位置A,重力做负功。这种情况下上式的关系是否还成立?
初状态B
=
末状态A
势能
动能
势能
动能
mgh1
mgh2
等式两边相加得:
忽略阻力,只有重力做功
只有弹力做功的系统内
在只有重力或弹簧弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。
表达式:
守恒条件
只有系统内动能和势能相互转化,无其他形式能量之间(如内能)的转化。
只受重力或弹力,不受其它力。
常见的机械能守恒的例子:
①自由落体运动
②平抛运动(抛体)
③单摆(秋千)
④在光滑斜面上滑动的物体。
①从能量的观点看:
②从力的观点看:
课堂练习
例1:在下面列举的各个实例中(除A外都不
计空气阻力),哪些过程中机械能是守恒的?
说明理由
A.跳伞运动员带着张开的降落伞在空气中匀速下落
B.抛出的标枪在空中运动
C.拉着一个金属块使它沿光滑的斜面匀速上升
D、在光滑水平面上运动的小球碰到一个弹簧,把弹簧压缩后,又被弹回来
抓住只有重力或弹力做功的条件。
f阻做功
拉力做功
BD
课本例题:把一个小球用细绳悬挂起来,就成为一个摆,摆长为l,最大偏角为θ。小球运动到最低位置时的速度是多大?
T
mg
v
初状态A
=
末状态O
势能
动能
势能
动能
0
mgh
解:
0
lcosθ
h=l-lcosθ
用机械能守恒定律求解
左边相加等于右边相加:
W
=
Ek2
—
Ek1
0
重力做正功:mgh
解:
以小球为研究对象,运用动能定理。
左边相加等于右边:
h=l-lcosθ
满足机械能守恒的条件,只需考虑运动的初状态和末状态,不必考虑两个状态间过程的细节。
初状态的θ角越大,cosθ越小,(1
-
cosθ)就越大,v也就越大。也就是说,最初把小球拉得越高,它到达最低点时的速度也就越大。
初状态
=
末状态
势能
动能
势能
动能
课堂练习
质量为m的小球从光滑曲面上滑下。当它到达高度为h1的位置A时,速度的大小为v1,滑到高度为h2的位置B时,速度的大小为v2。在由高度h1滑到高度h2的过程中,重力做的功为W。
(1)根据动能定理列出方程,描述小球在A、B两点间动能的关系。
mg
FN
,支持力不做功,只有重力做功。
解:受力分析
W
=
Ek2
—
Ek1
mgh
左边相加等于右边:
h=h1-h2
(2)
根据重力做功与重力势能的关系,把以上方程变形,以反映出小球运动过程中机械能是守恒的。
h=h1-h2
初状态
=
末状态
势能
动能
势能
动能
解:以山脚为0势能面
mgh1
mgh2
左边相加等于右边相加:
一、动能与势能的相互转化
机械能=
动能+势能
重力势能、弹性势能与动能之间可以相互转化,我们把它们统称为机械能。
二、机械能守恒定律
在只有重力或弹簧弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。
E机2=E机1
表达式:
课堂小结
重力势能
弹性势能
守恒条件
只有系统内动能和势能相互转化,无其他形式能量之间(如内能)的转化。
只受重力或弹力,不受其它力。
常见的机械能守恒的例子:
①自由落体运动
②平抛运动(抛体)
③单摆(秋千)
④在光滑斜面上滑动的物体。
①从能量的观点看:
②从力的观点看:
