第4章 三角形章节提优练（含解析）

中小学教育资源及组卷应用平台
2020-2021学年北师大版数学七年级下册章节提优练
第4章
《三角形》
试卷满分：100分
考试时间：120分钟
阅卷人
???
得分
???
一、选择题（共10题；每题2分，共20分）
1.
（2020七上·松桃月考）若等腰三角形的一个内角是40°，则这个等腰三角形的其他内角的度数为（??
）
A.?40°100°?B.?70°70°???C.?40°100°或70°70°???D.?以上都不对
2.
（2020七上·沂源期中）如图，在
中，
，
是三角形的重心，那么图中全等的三角形的对数是（???
）
A.?5???B.?6??C.?7???D.?8
3.
（2020七上·沂源期中）下列结论正确的个数有（???
）
①有两边和一角对应相等的两个三角形全等；
②三角形三边的垂直平分线相交于一点；
③有两边及夹角对应相等的两个三角形全等；
④三角形三个内角的角平分线有可能相交于三角形的外部．
A.?0个????B.?1个?C.?2个??D.?3个
4.
（2020七下·渭滨期末）如图，AE是△ABC的角平分线，AD⊥BC于点D，点F为BC的中点，若∠BAC＝104°，∠C＝40°，则有下列结论：①∠BAE＝52°；②∠DAE＝2°；③EF＝ED；④S△ABF＝
S△ABC.其中正确的个数有（?
）
A.?1个????B.?2个?????C.?3个?????D.?4个
5.
（2020七下·惠山期末）若三角形的三边长分别为4、x、7，则x的值可以是（??
）
A.?2???????B.?3????C.?8???D.?11
6.
（2020七上·沂源期中）如图，
的内角
平分线
与外角
的平分线交于点
，过
作
分别交
于
两点．下列结论：①
；②
；③
；④
，其中正确的结论有（???
）
A.?只有①②③???B.?只有①②④?????C.?只有③④??D.?①②③④
7.
（2020七下·长沙期末）如图，已知AC平分∠DAB，CE⊥AB于E，AB=AD+2BE，则下列结论：①AB+AD=2AE；②∠DAB+∠DCB=180°；③CD=CB；④S△ACE﹣2S△BCE=S△ADC；其中符合题意结论的个数是（　　）??
A.?1个???????B.?2个????C.?3个?????D.?4个
8.
（2020七下·宁德期末）如图，点P在∠MAN的角平分线上，点B，C分别在AM，AN上，作PR⊥AM，PS⊥AN，垂足分别是R，S．若∠ABP+∠ACP=180°，则下面三个结论：①AS=AR；②PC∥AB；③△BRP≌△CSP．其中正确的是（???
）
A.?①②????????B.?②③???????C.?①③???????D.?①②③
9.
（2020七下·哈尔滨期中）如图，BE和CE分别为△ABC的内角平分线和外角平分线，BE⊥AC于点H，CF平分∠ACB交BE于点F连接AE．则下列结论：①∠ECF=90°；②AE=CE；③
；④∠BAC=2∠BEC；⑤∠AEH=∠BCF，正确的个数为（???
）
A.?2个???????B.?3个???????C.?4个???D.?5个
10.
（2019七下·吴江期末）如图，
，
、
、
分别平分
、
和
。以下结论:①
;②
;③
;④
.?
其中正确的结论是（
??）
A.?①②③????B.?②③④????C.?①③④??????????D.?①②④
阅卷人
???
得分
???
二、填空题（共10题；每题2分，共20分）
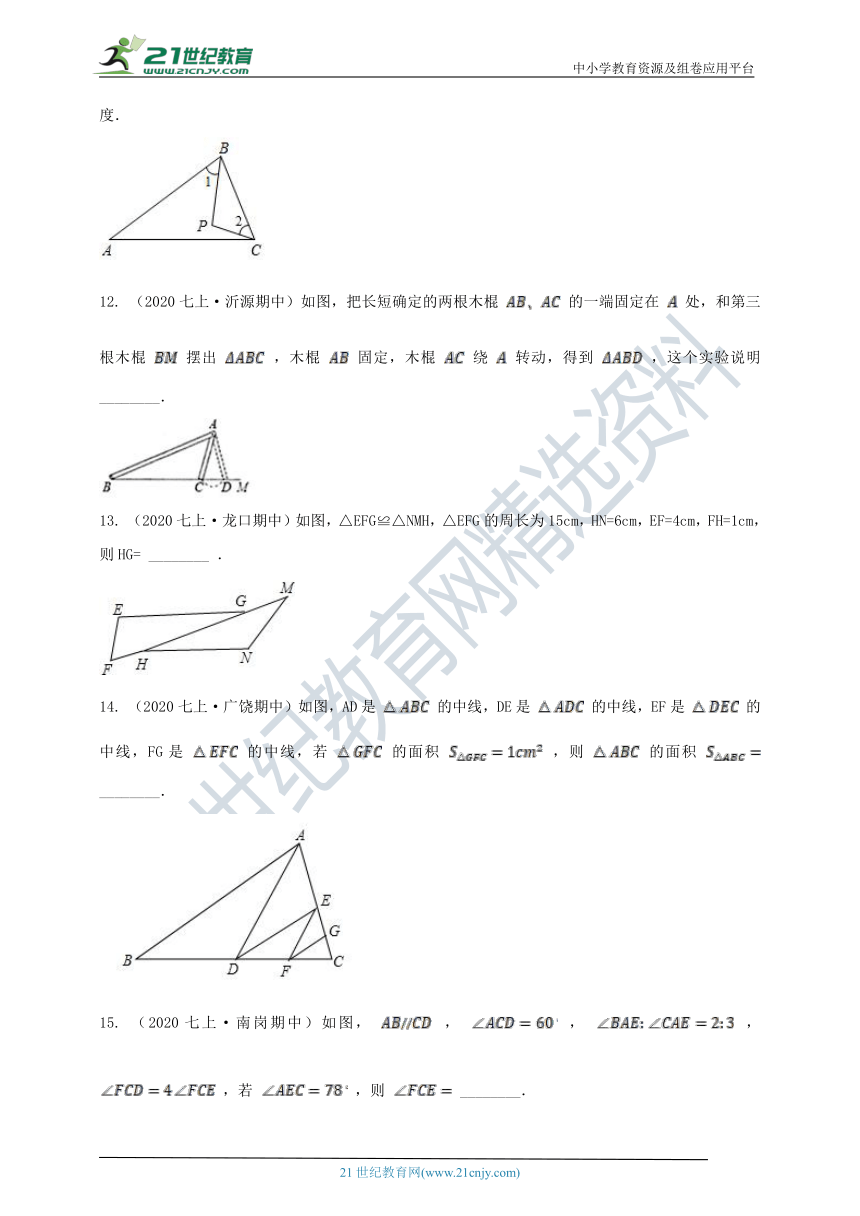
11.
（2020七上·广饶期末）如图，点P是△ABC内一点，∠ABC=80°，∠1=∠2，则∠BPC=________度．
12.
（2020七上·沂源期中）如图，把长短确定的两根木棍
的一端固定在
处，和第三根木棍
摆出
，木棍
固定，木棍
绕
转动，得到
，这个实验说明________．
13.
（2020七上·龙口期中）如图，△EFG≌△NMH，△EFG的周长为15cm，HN=6cm，EF=4cm，FH=1cm，则HG=
________
．
14.
（2020七上·广饶期中）如图，AD是
的中线，DE是
的中线，EF是
的中线，FG是
的中线，若
的面积
，则
的面积
________．
15.
（2020七上·南岗期中）如图，
，
，
，
，若
，则
________．
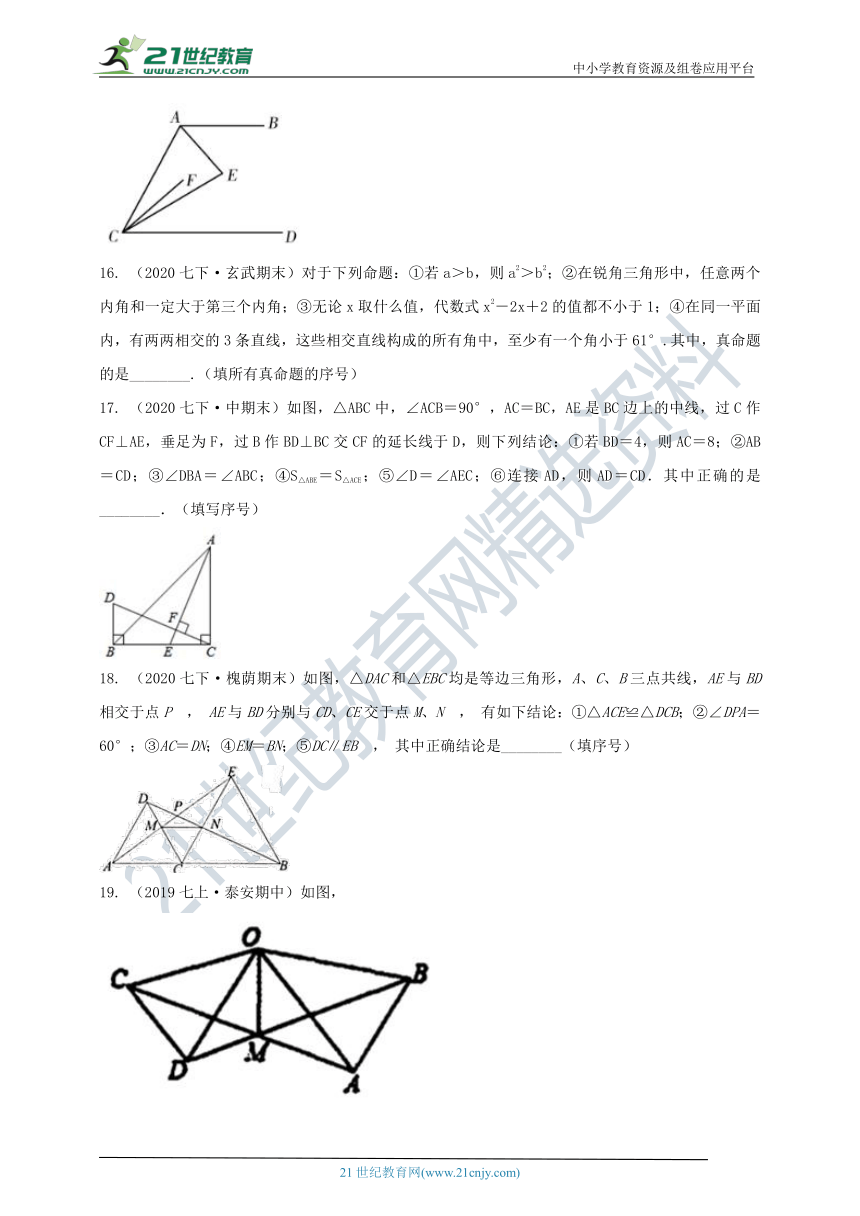
16.
（2020七下·玄武期末）对于下列命题：①若a＞b，则a2＞b2；②在锐角三角形中，任意两个内角和一定大于第三个内角；③无论x取什么值，代数式x2－2x＋2的值都不小于1；④在同一平面内，有两两相交的3条直线，这些相交直线构成的所有角中，至少有一个角小于61°.其中，真命题的是________.（填所有真命题的序号）
17.
（2020七下·中期末）如图，△ABC中，∠ACB＝90°，AC＝BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D，则下列结论：①若BD＝4，则AC＝8；②AB＝CD；③∠DBA＝∠ABC；④S△ABE＝S△ACE；⑤∠D＝∠AEC；⑥连接AD，则AD＝CD．其中正确的是________．（填写序号）
18.
（2020七下·槐荫期末）如图，△DAC和△EBC均是等边三角形，A、C、B三点共线，AE与BD相交于点P
，
AE与BD分别与CD、CE交于点M、N
，
有如下结论：①△ACE≌△DCB；②∠DPA＝60°；③AC＝DN；④EM＝BN；⑤DC∥EB
，
其中正确结论是________（填序号）
19.
（2019七上·泰安期中）如图，
在
和
.
，
，
，
，连接
，
交于点M，连接
，下列结论：①
；②
；③
平分
；④
平分
，其中正确的序号是________．
20.
（2019七下·苏州期末）如图，
中，
.点
从点
出发沿
路径向终点
运动；点
从
点出发沿
路径向终点
运动.点
和
分别以1和3的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过
和
作
于
，
于
.则点
运动时间等于________时，
与
全等。
阅卷人
???
得分
???
三、解答题（共9题；共60分）
21.
(
5分
)
（2020七上·广饶期中）在△ABC.∠A=35°，∠B=69°，
CD⊥AB于点D，CE平分∠ACB，
DP⊥CE于点P，求∠CDP的度数．
22.
(
5分
)
（2020七下·张家港期末）如图，
，将纸片的一角折叠，使点
落在
外，
若
，求
的度数.
23.
(
5分
)
（2020七下·沭阳期末）已知：如图所示，AB＝AD，BC＝DC，E、F分别是DC、BC的中点，求证：
AE＝AF。
24.
(
5分
)
（2020七下·新蔡期末）如图，在ΔABC中，已知∠ABC=60°，∠ACB=54°，BE是AC边上的高，CF是AB边上的高，H是BE和CF的交点，HD是∠BHC的平分线，求∠ABE、∠ACF和∠CHD的度数.
25.
(
5分
)
（2020七下·焦作期末）两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连结
.
请猜想：
与
的数量及位置关系，并说明理由.
26.
(
5分
)
（2020七下·鼓楼期末）用两种方法证明“三角形的外角和等于360°”；如图，
∠BAE、∠CBF、∠ACD是△ABC的三个外角.求证：∠BAE+∠CBF+∠ACD=360°
证法1：∵∠BAE、∠CBF、∠ACD是△ABC的三个外角
∴__
_.
∴∠BAE+∠CBF+∠ACD=2（∠1+∠2+∠3）
∵_
_
.
∴∠BAE+∠CBF+∠ACD=360°
请把证法1补充完整，并用不同的方法完成证法2
27.
(
7分
)
（2019七上·大庆期末）如图，在△ABC中，∠ABC为锐角，点D为直线BC上一动点，以AD为直角边且在AD的右侧作等腰直角三角形ADE，∠DAE＝90°，AD＝AE．
（1）如果AB＝AC，∠BAC＝90°．①当点D在线段BC上时，如图1，线段CE、BD的位置关系为________，数量关系为________
②当点D在线段BC的延长线上时，如图2，①中的结论是否仍然成立，请说明理由．
（2）如图3，如果AB≠AC，∠BAC≠90°，点D在线段BC上运动。探究：当∠ACB多少度时，CE⊥BC？请说明理由．
28.
(
10分
)
（2020七下·江都期末）如图，方格纸中每个小正方形的边长均为1，△ABC的三个顶点都在小正方形的顶点（小正方形的顶点叫格点）上.
（1）利用格点在图中画出△ABC中AB边上的高CD；
（2）①画出将△ABC先向右平移3格，再向下平移2格得到的△A1B1C1；
②线段
与
的数量关系与位置关系是
；
③在平移的过程中，线段AB扫过的部分所组成的封闭图形的面积为
.
29.
(
13分
)
（2020七上·沂源期中）
中，
是
的角平分线，
是
的高．
（1）如图1，若
，请说明
的度数；
（2）如图2（
），试说明
的数量关系；
（3）如图3，延长
到点
，
和
的角平分线交于点
，请求出
的度数．
答案解析
一、选择题
1.【答案】
C
解：①当这个角为顶角时，底角=（180°-40°）÷2=70°；
②当这个角是底角时，底角=40°，顶角为180°-2×40°=100°；
综上：其它两个内角的度数为70°，70°或40°，100°.
故答案为：C.
【分析】根据题意，分情况讨论：①当已知的40°的角是顶角时，②当已知的40°的角为底角时，再利用三角形的内角和定理求出其它两个角的度数.
2.【答案】
C
∵G是三角形的重心，
∴D、E.F分别是AB、AC、BC的中点，
又AB=AC
，
∴△ABF≌△ACF,△ABG≌△ACG,△ADG≌△AEG,△BGF≌△CGF,△BCD≌△CBE,△BDG≌△CED,△ACD≌△ABE
，
共7对全等三角形．
故答案为：C．
【分析】三角形的重心即三角形各边中线的交点，再由题中AB=AC，进而可得出题中所有的全等三角形．
3.【答案】
C
解：①有两边和一角对应相等的两个三角形全等，说法不符合题意，必须是夹角；
②三角形三边的垂直平分线相交于一点，说法符合题意；
③有两边及夹角对应相等的两个三角形全等，说法符合题意；
④三角形三个内角的角平分线不可能相交于三角形的外部，说法不符合题意．
综上，②③符合题意，共2个．
故答案为：C．
【分析】根据全等三角形的判定SAS定理可得①不符合题意；根据线段垂直平分线的定义可得三角形三边的垂直平分线相交于一点，故②符合题意；根据全等三角形的判定SAS定理可得③符合题意；根据三角形三个内角的角平分线的定义可得④不符合题意．
4.【答案】
C
解：∵AE是△ABC的角平分线，∠BAC＝104°，
∴∠BAE=∠CAE＝
=52°；
①正确；
∵AD⊥BC，∠C＝40°，
∴∠CAD=90°-40°=50°；
∴∠DAE＝∠CAE
-∠CAD
=2°；
②正确；
∵F为BC的中点，
∴S△ABF＝
S△ABC.???
④正确.
根据已知条件不能够判定③正确.
综上，正确的结论为①②④，共3个，
故答案为：C.
【分析】根据角平分线的定义可判定①,根据角平分线的定义及垂直的定义求得∠CAE=52°,∠CAD=50°,再由∠DAE＝∠CAE
-∠CAD即可判定②；根据三角形中线的性质即可判定④；③根据已知条件判定不出，由此即可解答.
5.【答案】
C
解：∵三角形的三边长分别为4，7，x，
∴7﹣4＜x＜7+4，即3＜x＜11.
∴8符合题意，
故答案为：C.
【分析】根据三角形的三边关系列出不等式即可求出x的取值范围，然后确定可能值即可.
6.【答案】
B
解：过D作DM⊥AB，DN⊥CB，DO⊥EF，
∵S△EBD＝
?BE?DM，S△FBD＝
?BF?DN，BD是∠EBC的平分线，DM⊥AB，DN⊥CB，
∴DM＝DN，
∴S△EBD：S△FBD＝BE：BF，①符合题意；
∵DE是∠AEF的平分线，
∴AD＝DO，
∵DB是∠ABC的平分线，
∴DA＝DN，
∴DO＝DN，
∴DF是∠EFC的平分线，
∴∠EFD＝∠CFD，②符合题意；
∵HD∥BF，
∴∠HDB＝∠FBD，
又∵BD平分∠ABC，
∴∠HBD＝∠CBD，
于是∠HBD＝∠HDB，
故HB＝HD．
但没有条件说明HF与HB必然相等，③不符合题意；
由于点D为△BEF的内角∠EBF平分线BD与外角∠AEF的平分线的交点，
故D为△BEF的内心，
于是FD为∠EFC的平分线，
故∠CFD＝∠EFD，
又∵DH∥BC，
∴∠HDF＝∠CFD，
故∠GDF＝∠DFE，
于是GF＝GD，
又∵HB＝HD，
∴HD?GD＝HG，
即BH?GF＝HG，④符合题意．
故①②④符合题意．
故答案为：B．
【分析】①根据三角形的面积公式，以及角平分线的性质定理可直接得出答案；②根据角平分线的性质解答即可；③根据平行线的性质和角平分线的性质，判断出∠HBD＝∠HDB，根据等角对等边即可证出HB＝HD，但根据现有条件不能的出HF与HB必然相等的结论；④根据三角形角分线的性质，判断D为内心，进而得出∠CFD＝∠EFD，再根据平行线的性质，得出∠HDF＝∠CFD，从而判断出∠GDF＝∠DFE，于是可得，HB＝HD，再通过等量代换和线段的加减法则即可得出结论．
7.【答案】
C
解：①在AE取点F，使EF=BE，
∵AB=AD+2BE=AF+EF+BE，EF=BE，
∴AB=AD+2BE=AF+2BE，
∴AD=AF，
∴AB+AD=AF+EF+BE+AD=2AF+2EF=2（AF+EF）=2AE，
∴AE=
（AB+AD），故①符合题意；
②在AB上取点F，使BE=EF，连接CF．
在△ACD与△ACF中，∵AD=AF，∠DAC=∠FAC，AC=AC，
∴△ACD≌△ACF，
∴∠ADC=∠AFC．
∵CE垂直平分BF，
∴CF=CB，
∴∠CFB=∠B．
又∵∠AFC+∠CFB=180°，
∴∠ADC+∠B=180°，
∴∠DAB+∠DCB=360-（∠ADC+∠B）=180°，故②符合题意；
③由②知，△ACD≌△ACF，∴CD=CF，
又∵CF=CB，
∴CD=CB，故③符合题意；
④易证△CEF≌△CEB，
所以S△ACE-S△BCE=S△ACE-S△FCE=S△ACF
，
又∵△ACD≌△ACF，
∴S△ACF=S△ADC
，
∴S△ACE-S△BCE=S△ADC
，
故④不符合题意；
即正确的有3个，
故答案为：C．
【分析】①在AE取点F，使EF=BE．利用已知条件AB=AD+2BE，可得AD=AF，进而证出2AE=AB+AD；②在AB上取点F，使BE=EF，连接CF．先由SAS证明△ACD≌△ACF，得出∠ADC=∠AFC；再根据线段垂直平分线、等腰三角形的性质得出∠CFB=∠B；然后由邻补角定义及四边形的内角和定理得出∠DAB+∠DCB=180°；
③根据全等三角形的对应边相等得出CD=CF，根据线段垂直平分线的性质得出CF=CB，从而CD=CB；④由于△CEF≌△CEB，△ACD≌△ACF，根据全等三角形的面积相等易证S△ACE-S△BCE=S△ADC
．
8.【答案】
C
解：∵点
P
在∠MAN的角平分上，PR⊥AM，
PS⊥AN，
∴PR=PS，
∵∠ARP=∠ASP=90°，
∴在Rt△APR和Rt△APS中，
，
∴△APR≌△APS（HL），
∴AS=AR，故①符合题意；
∵∠ABP
+∠ACP
=
180°，
∴∠ABP=∠PCS，
又∵PR=PS，∠PRB=∠PSC=90°，
∴△BRP≌△CSP（AAS），故③符合题意；
若∠MAP=∠CPA，则PC∥AB，
则需要AC=PC得出∠PAN=∠CPA，
从而根据∠MAP=∠PAN，
得出∠MAP=∠CPA，
而题中没有条件说明AC=PC，故②不符合题意；
故答案为：C．
【分析】利用角平分线的性质得到PR=PS，再利用HL证明△APR≌△APS，得到AS=AR，可判断①；再根据∠ABP
+∠ACP
=
180°，得到∠ABP=∠PCS，再利用AAS证明△BRP≌△CSP可判断③；再说明若要PC∥AB
，
则需要说明AC=PC，无法达成，从而可判断②.
9.【答案】
D
解：∵AE平分
，CF平分
，
∴
，
∴
，故①符合题意；
∵BE平分
，
于点H，
∴
，
，
∴
，
∴
，
∵
，
，
∴
，
∴
，故②符合题意；
∵BE平分
，CF平分
，
∴
，
又∵
即有：
，故③符合题意；
∵
，
∴
，
又∵
，CF平分
，
∴
，
∴
即：
，故④符合题意；
∵
，CF平分
，
∴
，
，
，
∴
，故⑤符合题意；
综上所述，正确的有：①②③④⑤，共5个，
故答案为：D．
【分析】根据AE平分
，CF平分
，可得
，
则易证
，可判断①符合题意；根据BE平分
，
于点H，可证
，得到
，可证
，则有
，可判断②符合题意；根据BE平分
，CF平分
，得到
，
，则利用
可以判断③；根据
，
，得到
，利用
，CF平分
，得
，可以判断④符合题意；根据
，CF平分
，得到
，
，
，
，故可以判断⑤符合题意；
10.【答案】
D
解：①∵AD平分△ABC的外角∠EAC，
∴∠EAD=∠DAC，
∵∠EAC=∠ACB+∠ABC，且∠ABC=∠ACB，
∴∠EAD=∠ABC，
∴AD∥BC，
故①正确.
②由（1）可知AD∥BC，
∴∠ADB=∠DBC，
∵BD平分∠ABC，
∴∠ABD=∠DBC，
∴∠ABC=2∠ADB，
∵∠ABC=∠ACB，
∴∠ACB=2∠ADB，
故②正确.
③∵∠BAC+∠ABC=∠ACF，
∴
∠BAC+
∠ABC=
∠ACF，
∵∠BDC+∠DBC=
∠ACF，
∴
∠BAC+
∠ABC=∠BDC+∠DBC，
∵∠DBC=
∠ABC，
∴
∠BAC=∠BDC，即∠BDC=
∠BAC.
故③错误.
④在△ADC中，∠ADC+∠CAD+∠ACD=180°，
∵CD平分△ABC的外角∠ACF，
∴∠ACD=∠DCF，
∵AD∥BC，
∴∠ADC=∠DCF，∠ADB=∠DBC，∠CAD=∠ACB
∴∠ACD=∠ADC，∠CAD=∠ACB=∠ABC=2∠ABD，
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°，
∴∠ADC+∠ABD=90°
∴∠ADC=90°-∠ABD，
故④正确。
故答案为：D。
【分析】根据角平分线的定义得出∠EAD=∠DAC，根据三角形的一个外角等于与之不相邻的两个内角的和得出∠EAC=∠ACB+∠ABC，又∠ABC=∠ACB，故∠EAD=∠ABC，根据同位角相等两直线平行得出AD∥BC，故①正确；②根据二直线平行内错角相等得出∠ADB=∠DBC，根据角平分线的定义得出∠ABC=2∠DBC=2∠ADB，又∠ABC=∠ACB，所以∠ACB=2∠ADB，故②正确；③根据三角形的一个外角等于与之不相邻的两个内角的和得出∠BAC+∠ABC=∠ACF，故
∠BAC+
∠ABC=
∠ACF，又根据三角形的外角定理得出∠BDC+∠DBC=
∠ACF，根据等式的传递性得出
∠BAC+
∠ABC=∠BDC+∠DBC，又∠DBC=
∠ABC，所以∠BDC=
∠BAC，故③错误；④根据三角形的内角和得出∠ADC+∠CAD+∠ACD=180°，根据二直线平行，内错角相等得出∠ADC=∠DCF，∠ADB=∠DBC，∠CAD=∠ACB，故∠ACD=∠ADC，∠CAD=∠ACB=∠ABC=2∠ABD，从而利用等量代换及等式的性质得出∠ADC+∠ABD=90°，即∠ADC=90°-∠ABD，故④正确。
二、填空题
11.【答案】
100
解：∵∠ABC=80°，∠1=∠2，
∴
故答案为：100．
【分析】由于∠1=∠2，利用三角形内角和定理得出=
，
据此计算即得.
12.【答案】
有两边和其中一边的对角分别相等的两个三角形不一定全等
解：由题意可知：AB=AB，AC=AD，∠ABC=∠ABD，
满足有两边和其中一边的对角分别相等，但是△ABC与△ABD不全等，所以这个实验说明有两边和其中一边的对角分别相等的两个三角形不一定全等，
故答案为：有两边和其中一边的对角分别相等的两个三角形不一定全等．
【分析】根据全等三角形的判定方法解答即可．
13.【答案】
4cm
解：∵△EFG≌△NMH，
∴MN=EF=4cm，FG=MH，△HMN的周长=△EFG的周长=15cm，
∴FG-HG=MH-HG，即FH=GM=1cm，
∵△EFG的周长为15cm，
∴HM=15-6-4=5cm，
∴HG=5-1=4cm
.
故答案为4cm．
【分析】首先根据全等三角形对应边相等可得MN=EF=4cm，FG=MH，△HMN的周长=△EFG的周长=15cm，再根据等式的性质可得FG-HG=MH-HG，即GM=FH，进而可得答案．
14.【答案】
解：
是
的中线，
，
同理可得：
，
，
，
，
，
故答案为：
．
【分析】根据三角形中线与三角形的面积关系即可得．
15.【答案】
解：∵
，
∴
∵
∴
∵
∴
∴
∵
∴
．
故答案是：
【分析】利用平行线的性质得出由
，
可求出∠CAE=72°，根据三角形内角和可得
，
从而得出
，
由
，
可得出
，
据此即得结论.
16.【答案】
②③④
解：①当a=-1，b=-2时，满足a＞b，但a2＜b2；原命题是假命题；
②在锐角三角形中，若任意两个内角和小于第三个内角，则这三个角的和小于180°，是真命题；
③无论x取什么值，代数式x2-2x+2=(x-1)2+1≥1，所以其值都不小于1，是真命题；
④如图1，当三条直线如图1相交时，若每个角都不小于61°，
则∠1+∠2+∠3>180°，这与平角定义相矛盾，
∴至少有一个角小于61°；
当三条直线如图2相交时，若每个角都不小于61°，则∠1+∠2+∠3>180°，这与三角形内角和定理相矛盾，
∴至少有一个角小于61°；
综上可知，在同一平面内，有两两相交的3条直线，这些相交直线构成的所有角中，至少有一个角小于61°，是真命题.
故答案为：②③④.
【分析】
①?举一个反例即可否定；
②
用反证法证明，推出假设和三角形内角和定理相矛盾；
③
配方，可用完全平方式的非负性来验证；④用反证法证明，推出假设和平角的定义或三角形内角和定理相矛盾.
17.【答案】
①③④⑤⑥
解：∵∠ACB＝90°，AC＝BC，
∴∠BAC＝∠ABC＝45°，
∵BD⊥BC，∴∠DBA＝90°﹣∠ABC＝45°，
∴∠DBA＝∠ABC，故③符合题意；
∵AE是BC边上的中线，∴BE＝CE，
∴S△ABE＝S△ACE
，
故④符合题意；
∵CF⊥AE，∴∠EAC+∠FCA＝90°，
又∵∠BCD+∠FCA＝90°；
∴∠BCD＝∠EAC，
∴在△DBC和△ECA中，
，
∴△DBC≌△ECA
（ASA），
∴BD＝EC，∠D＝∠AEC，故⑤符合题意；
∴AC＝BC＝2EC＝2BD，
当BD＝4，则AC＝8，故①符合题意；
∵△DBC≌△ECA，
∴CD＝AE，
∵AB≠AE，
∴AB≠CD，故②不符合题意；
如图，连接AD，过D作DG⊥AC交AC于G，则DG∥BC，
∵DB⊥BC，GC⊥BC，
∴BD＝CG＝EC，
∴G为AC的中点，
∴AD＝CD，故⑥符合题意．
故答案为：①③④⑤⑥．
【分析】根据等腰三角形的性质和角的和差即可判断③；根据三角形中线的性质即可判断④；根据ASA可证明△DBC≌△ECA，进而可由全等三角形的性质判断①⑤②；如图，连接AD，过D作DG⊥AC交AC于G，由平行线间的距离处处相等和线段垂直平分线的性质即可判断⑥，进而可得答案．
18.【答案】
①②④⑤
解：∵△DAC和△EBC都是等边三角形，
∴∠ACD=∠BCE=60°，
∴∠ACE=∠DCB=120°，
在△ACE与△DCB中，
∴△ACE≌△DCB（SAS），故①符合题意；
在△DMP和△ACM中
∵△ACE≌△DCB，
∴∠BDC=∠EAC
又∠DMP=∠AMC
∴∠DPA=∠DCA=60°，故②符合题意；
∵△ACE≌△DCB，
∴∠BDC=∠EAC
又∠ACD=∠BCE=60°，AC=CD
在△ACM和△DCN中
∴△ACM≌△DCN（ASA）
∴AM=DN
又根据三角形外角性质得到∠AMC＞∠MCE，
则∠AMC＞∠ACM，
∴AC＞AM
∴AC＞DN，故③不符合题意；
由②中△ACM≌△DCN可得AM=DN
又△ACE≌△DCB
∴AE=DB
∴EM=BN，故④符合题意；
∵△DAC和△EBC均是等边三角形，
∴∠ACD=∠BCE=60°，
∴∠DCE=60°，
∴∠DCE=∠BEC，
∴CD∥BE，故⑤符合题意．
故答案为：①②④⑤
【分析】①根据等边三角形的性质可得AC=CD，BC=CE，∠ACD=∠BCE=60°，然后求出∠ACE=∠BCD，利用“边角边”证明△ACE和△DCB全等；②通过△ACE和△DCB全等，可得到∠BDC=∠EAC，在△DMP和△ACM中，利用“8”字型可求得∠DPA=∠DCA=60°；③根据三角形外角性质得到∠AMC＞∠MCE，则∠AMC＞∠ACM，所以AC＞AM，又可证得△ACM和△DCN全等，得到AM=DN，从而得到AC＞DN；④根据全等三角形对应边相等可得AM=DN，CM=CN，然后求出EM=BN；⑤△DAC和△EBC均是等边三角形，所以∠ACD=∠BCE=60°，可得到∠DCE=60°，所以∠DCE=∠BEC，再根据内错角相等，两直线平行可得CD∥BE．
19.【答案】
①②④
解：∵∠AOB=∠COD=40
，
∴∠AOB+∠AOD=∠COD+∠AOD，
即∠AOC=∠BOD，
在△AOC和△BOD.
，
∴△AOC
△BOD，
∴∠OCA=∠ODB，AC=BD，①符合题意；
∵△AOC
△BOD
∴∠OAC=∠OBD，
由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD，
∴∠AMB=∠AOB=40
，
∴∠CMD=∠AMB=40
，②符合题意；
作OG⊥MC于G，OH⊥MB于H，如图2所示：
则∠OGC=∠OHD=90
，
在△OCG和△ODH.
，
∴△OCG
△ODH，
∴OG=OH，
∵OG⊥MC，OH⊥MB
∴MO平分∠BMC，④符合题意；
∵∠AOB=∠COD，
假设OM平分∠AOD，
∵OM平分∠AOD，
∴∠AOM=∠DOM，
∵△AOC≌△BOD，
∴∠COM=∠BOM，
∵MO平分∠BMC，
∴∠CMO=∠BMO，
在△COM和△BOM.
∴△COM≌△BOM(ASA)，
∴OB=OC，
∵OA=OB，
∴OA=OC，
与OA>OC矛盾，
故假设不成立，OM不平分∠AOD
∴③不符合题意；
故答案为：①②④
【分析】由SAS证明△AOC≌△BOD得出∠OCA=∠ODB，AC=BD，①符合题意；由全等三角形的性质得出∠OAC=∠OBD，由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD，得出∠AMB=∠AOB=40°，②符合题意；
作OG⊥MC于G，OH⊥MB于H，如图所示：则∠OGC=∠OHD=90°，由AAS证明△OCG≌△ODH（AAS），得出OG=OH，由角平分线的判定方法得出MO平分∠BMC，④符合题意；先假设OM平分∠AOD，推出OA=OC与条件中
相矛盾，推出③不符合题意．
20.【答案】
1或3.5或12秒
解：设运动时间为t秒时，△PEC≌△QFC，
∵△PEC≌△QFC，
∴斜边CP=CQ，
有四种情况：①P在AC上，Q在BC上，
CP=6-t，CQ=8-3t，
∴6-t=8-3t，
∴t=1；
②P、Q都在AC上，此时P、Q重合，
∴CP=6-t=3t-8，
∴t=3.5；
③P在BC上，Q在AC时，此时不存在；
理由是：8÷3×1＜6，Q到AC上时，P应也在AC上；
④当Q到A点（和A重合），P在BC上时，
∵CQ=CP，CQ=AC=6，CP=t-6，
∴t-6=6
∴t=12
∵t＜14
∴t=12符合题意。
故答案为：
1或3.5或12秒。
【分析】设运动时间为t秒时，根据全等三角形的性质，斜边CP=CQ，然后分类讨论：①P在AC上，Q在BC上，根据路程等于速度乘以时间及线段的和差得出CP=6-t，CQ=8-3t，从而列出方程求解即可；②P、Q都在AC上，此时P、Q重合，根据CP=6-t=3t-8，列出方程，求解即可；③P在BC上，Q在AC时，此时不存在；④当Q到A点（和A重合），P在BC上时，由于CQ=CP，CQ=AC=6，CP=t-6，从而列出方程，求解即可，综上所述即可得出答案。
三、解答题
21.【答案】
解：∵CD⊥AB，
∴∠BDC=90°，
∴∠BCD=90°-∠B=90°-69°=21°，
∵∠A+∠B+∠ACB=180°，
∴∠ACB=180°-35°-69°=76°，
∵CE平分∠ACB，
∴∠BCE=
∠ACB=38°，
∴∠DCE=∠BCE-∠BCD=38°-21°=17°
∵DP⊥CE，
∴∠DPC=90°，
∴∠CDP=90°-∠DCP=90°-17°=73°．
【解析】【分析】先由CD⊥AB得到∠BDC=90°，则利用互余计算出∠BCD=90°-∠B=21°，接着根据三角形内角和定理计算出∠ACB=76°，于是利用角平分线的定义得到∠BCE=
∠ACB=38°，所以∠DCE=∠BCE-∠BCD=17°，然后再利用互余计算∠CDP的度数．
22.【答案】
解：如图，
在
中，
由折叠可知
，?
所以
所以
【解析】【分析】由三角形内角和定理可得
，再根据折叠的性质可得
，再根据三角形外角的性质求解即可.
23.【答案】
证明：连接AC，
在△ACD和△ACB中，
，
∴△ACD≌△ACB（SSS），
∴∠ACE＝∠ACF，
∵BC＝DC，E，F分别是DC、BC的中点，
∴CE＝CF，
在△ACE和△ACF中，
，
∴△ACE≌△ACF（SAS），
∴AE＝AF.
【解析】【分析】连接AC，证△ACD≌△ACB可得∠ACE＝∠ACF，根据中点的性质知CE＝CF，利用“SAS”即可证明△ACE≌△ACF，可得AE＝AF.
24.【答案】
解：
，BE是AC边上的高，CF是AB边上的高，
【解析】【分析】根据已知角和垂线的定义即可得出
和
的度数，再根据角的和与差得出∠ABE、∠ACF的度数，进而根据三角形内角和即可得出
，最后根据角平分线的性质即可得出∠CHD的度数.
25.【答案】
解：
；
，
理由如下：
与
均为等腰直角三角形，
∴
，
，
.
，
∴
，
即∠
，
∴
，
∴
，
∴
，
又∵
，
∴
，∴
.
【解析】【分析】根据等腰直角三角形的性质，可以得出△ABE≌△ACD，得出对应边相等，∠B=∠ACD-45°，进而得出∠DCB=90°，就可以得出结论.
26.【答案】
证明：证法
、
、
是
的三个外角.
，
，
.
，
.
；
证法
平角等于
，
，
.
，
.
故答案为：
，
，
；
.
【解析】【分析】证法1：要求证
，根据三角形外角性质得到
，
，
，则
，然后根据三角形内角和定理即可得到结论；证法2：根据平角的定义得到
，再根据三角形内角和定理和角的和差关系即可得到结论.
27.【答案】
（1）①垂直；相等
②都成立，理由如下：
∵∠BAC＝∠DAE＝90°，
∴∠BAC＋∠DAC＝∠DAE＋∠DAC
，
∴∠BAD＝∠CAE
，
在△DAB与△EAC中，
?
∴△DAB≌△EAC
，
∴CE＝BD
，
∠B＝∠ACE
，
∴∠ACB＋∠ACE＝90°，即CE⊥BD
（2）解：当∠ACB＝45°时，CE⊥BD（如图）．
理由：过点A作AG⊥AC交CB的延长线于点G
，
则∠GAC＝90°，
∵∠ACB＝45°，∠AGC＝90°﹣∠ACB
，
∴∠AGC＝90°﹣45°＝45°，
∴∠ACB＝∠AGC＝45°，
∴AC＝AG
，
在△GAD与△CAE中，
?
∴△GAD≌△CAE
，
∴∠ACE＝∠AGC＝45°，
∠BCE＝∠ACB＋∠ACE＝45°＋45°＝90°，即CE⊥BC．
（1）：（1）CE与BD位置关系是CE⊥BD，数量关系是CE=BD．
理由：如图1，∵∠BAD=90°-∠DAC，∠CAE=90°-∠DAC，
∴∠BAD=∠CAE．
又
BA=CA，AD=AE，
∴△ABD≌△ACE
（SAS）
∴∠ACE=∠B=45°且
CE=BD．
∵∠ACB=∠B=45°，
∴∠ECB=45°+45°=90°，即
CE⊥BD．
故答案为：垂直，相等
【分析】（1）①根据∠BAD=∠CAE，BA=CA，AD=AE，运用“SAS”证明△ABD≌△ACE，根据全等三角形性质得出对应边相等，对应角相等，即可得到线段CE、BD之间的关系；
②先根据“SAS”证明△ABD≌△ACE，再根据全等三角形性质得出对应边相等，对应角相等，即可得到①中的结论仍然成立；（2）先过点A作AG⊥AC交BC于点G，画出符合要求的图形，再结合图形判定△GAD≌△CAE，得出对应角相等，即可得出结论．
28.【答案】
（1）解：BC边长为2，BC边上的高为点A
到BC的垂线长为4，
，而AB的长为
，根据面积公式，可知AB边的高为
，
如图：取格点E、F，连接BE、CF交于点D，CD即为所求
（2）解：①①将△ABC向右平移3格，再向下平移2格，所得图形如下所示：
；
；
；
；16，
解：（2）②∵
是由
平移所得，平移所得线段、平移的路径均平行且相等，
∴数量关系：
；位置关系：
.
③AB线段所扫过的面积如下图阴影划线部分所示：
重合部分面积
.
【分析】（1）根据
，且AB长为
，根据面积公式，可知AB边的高为
；取格点E、F，连接BE、CF交于点D，CD即为所求（2）①先找到图形的关键点A、B、C三点，分别把这三点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形；②平移所得线段、平移的路径均平行且相等，所以
的数量关系和位置关系便可得知；③将AB线段所扫过的面积在图形中表示出来，发现扫过的面积为两个平行四边形，用底乘以高分别计算出两个平行四边形的面积，再将面积求和，即可得到答案.
29.【答案】
（1）
是
的高，
是
的角平分线，
，
．
（2）
是
的高，
是
的角平分线，
，
即
（3）
和
的角平分线交于点
，
，即
，
是
的高，
，
．
【解析】【分析】（1）先根据三角形的内角和定理求得
、
，再根据角平分线的定义得到
，最后根据角的和差解答即可；（2）先根据三角形的内角和定理求得
、
，再根据角平分线的定义得到
，然后根据角的和差表示出来即可；（3）先根据角平分线的定义得到
，再结合三角形外角的性质得到
，然后根据题意得到
，最后算出∠G即可．
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)