18.2.1.1矩形的性质课件(25张)
图片预览



文档简介
(共25张PPT)
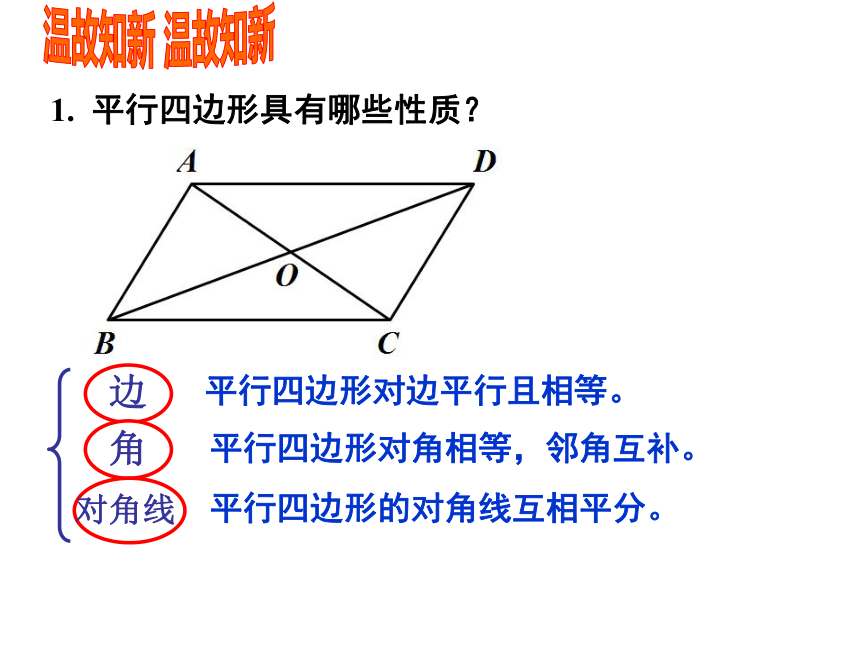
1. 平行四边形具有哪些性质?
平行四边形对边平行且相等。
平行四边形对角相等,邻角互补。
平行四边形的对角线互相平分。
边
角
对角线
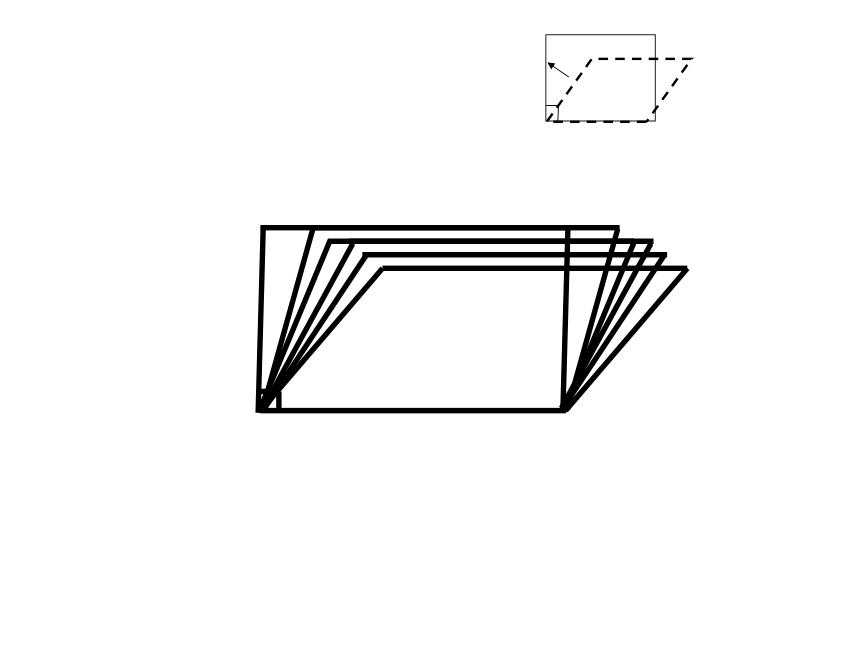
3.在推动平行四边形的变化过程中,你有没有
发现一种熟悉的、更特殊的图形?
2. 我们都知道三角形具有稳定性,
平行四边形是否也具有稳定性?
18.2.1 矩形(1)
18.2 特殊的平行四边形
2
学导目标 :
会初步运用矩形的概念和性质来解决有关问题.
掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
1
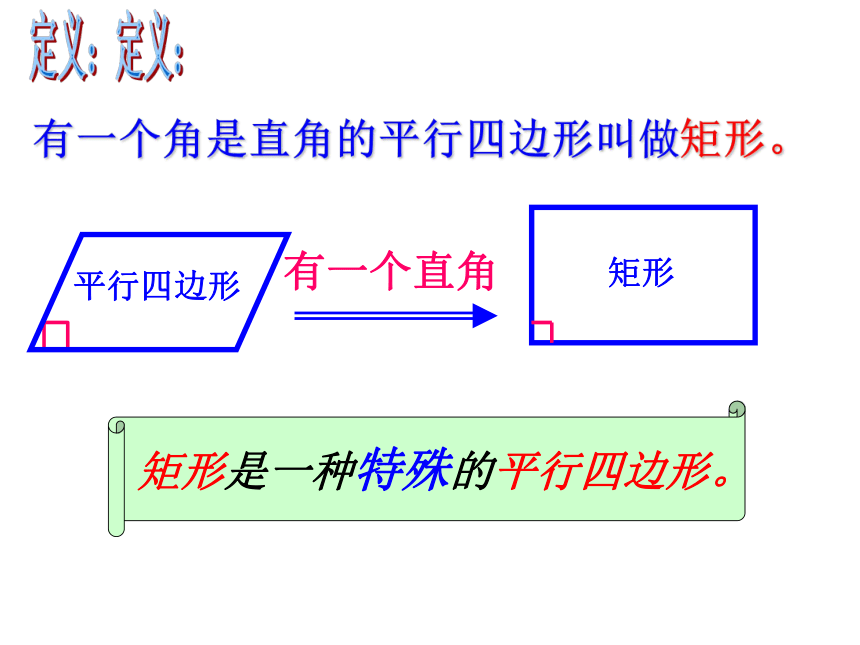
有一个角是直角的平行四边形叫做矩形。
有一个直角
平行四边形
矩形
矩形是一种特殊的平行四边形。
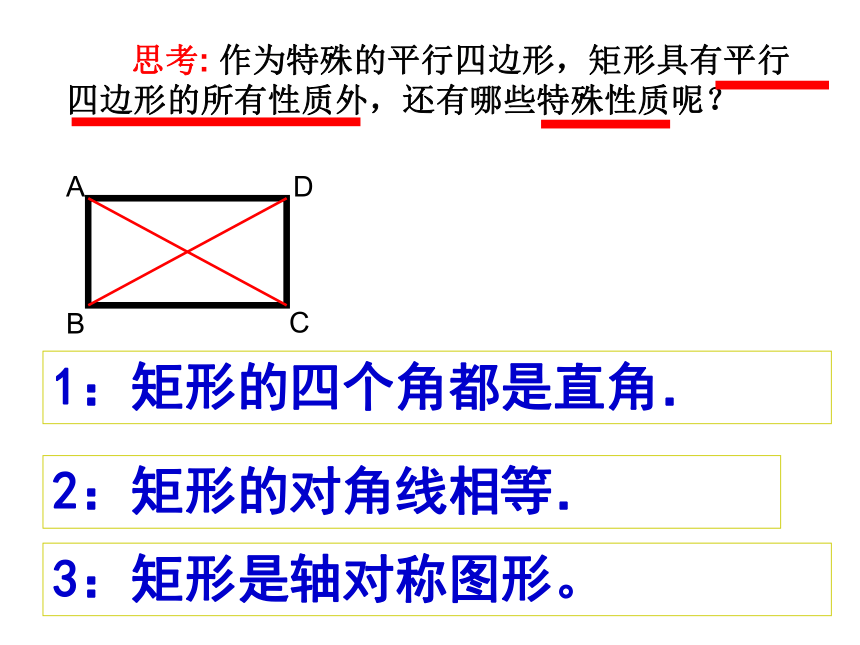
思考: 作为特殊的平行四边形,矩形具有平行四边形的所有性质外,还有哪些特殊性质呢?
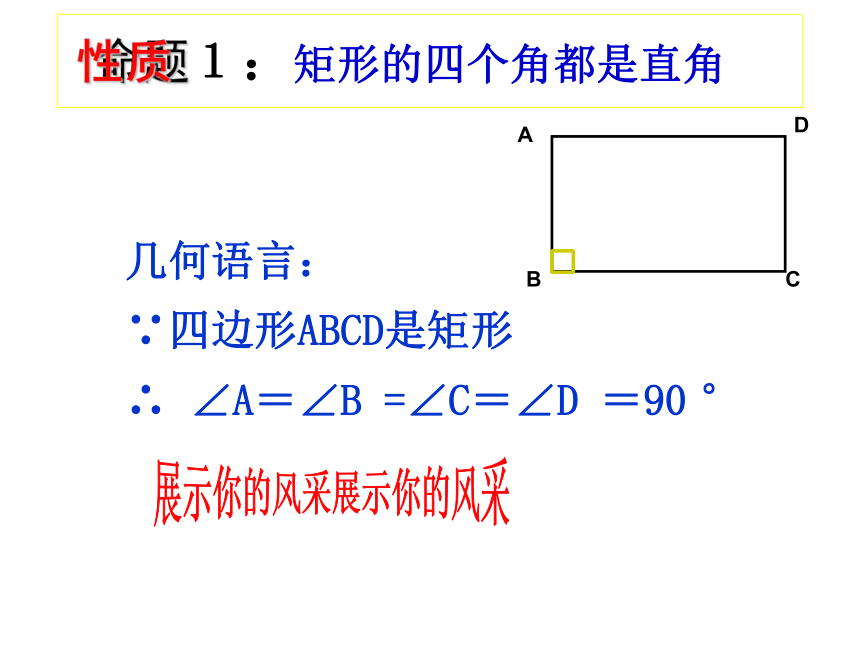
1:矩形的四个角都是直角.
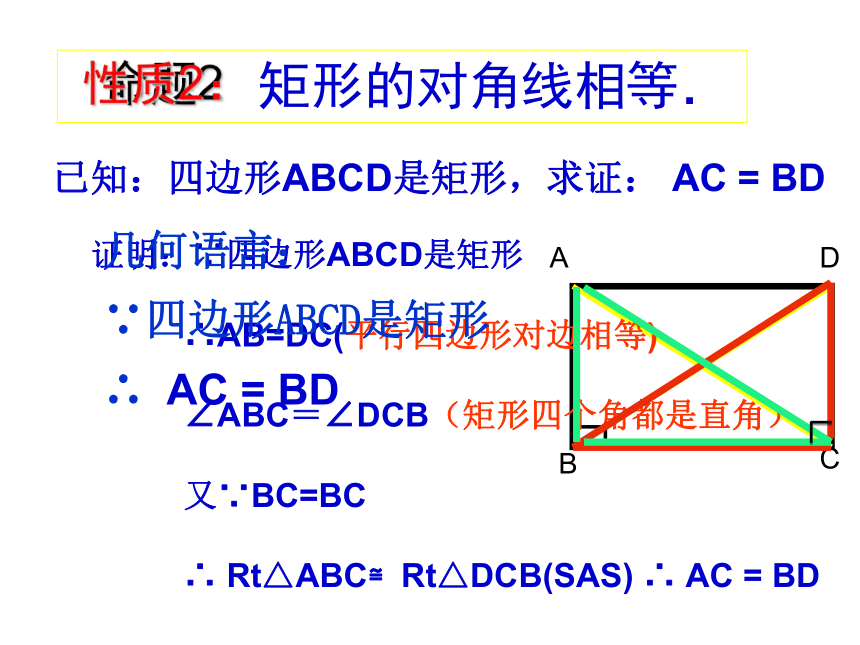
2:矩形的对角线相等.
A
B
C
D
3:矩形是轴对称图形。
1:矩形的四个角都是直角
D
C
B
A
命题
性质
几何语言:
∵四边形ABCD是矩形
∴ ∠A=∠B =∠C=∠D =90 °
已知:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
∵四边形ABCD是矩形
∴AB=DC(平行四边形对边相等)
∠ABC=∠DCB(矩形四个角都是直角)
又∵BC=BC
∴ Rt△ABC≌Rt△DCB(SAS) ∴ AC = BD
矩形的对角线相等.
命题2
性质2:
证明:
几何语言:
∵四边形ABCD是矩形
∴ AC = BD
理一理!! 矩形的所有性质:
B
C
D
A
从边看
从角看
从对角线看
从对称性看
对边分别平行且相等
对角相等,邻角互补,四个角都是直角
对角线相等且互相平分。
是轴对称图形
你在矩形中还发现了哪些基本图形?
A
B
C
D
O
A
B
C
D
O
◆ 四个全等的直角三角形.
A
B
C
D
O
◆ 四个等腰三角形.
矩形的对角线相等且互相平分.
性质2:
几何语言:
∵四边形ABCD是矩形
∴ AC = BD ,
OA=OB=OC=OD= AC= BD
O
A
B
D
C
O
C
D
B
A
┛
在Rt△ABC中,BO是斜边AC的中线
直角三角形的性质 :
直角三角形斜边上的中线等于斜边的一半。
则有:BO= AC
试试:用文字叙述
直角三角形的性质
思考:在Rt△ABC中,BO和AC是什么关系
矩形的定义中有两个条件:
一是 , 二是 .
挑战第一关--定义
有一个角是直角
平行四边形
挑战第二关--性质
1、矩形具有而一般平行四边形不具有的性质 ( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
2、如图,四边形ABCD是矩形,若AC=10,则BD=____
C
10
挑战第二关—性质
3、如图,已知Rt△ABC,∠ACB=900,CD是斜边AB上的中线,若CD=6,则AB=____
6
4、矩形是轴对称图形吗 几条对称轴?
12
7、研读课文p53例1,完成学导案例1
例1 如图,矩形ABCD的对角线AC、BD相
交于点O, ∠AOB= 60°,AB=4 ,求矩形对
角线的长.
矩形性质的运用
O
A
B
D
C
解:∵四边形ABCD是矩形,
∴OA=OB( )
又∠AOB= 60°,
∴△OAB是 三角形.
∴OA= .
∴AC=BD=2 = .
等边
AB=4
AB
2×4=8
矩形对角线相等且互相平分
挑战第三关---展示书写
已知:如图,四边形ABCD为矩形,∠AOB=60°,
BD=6.求AB、AD.
60°
随堂练习,巩固深化:
1、下列说法错误的是( ).
(A)矩形的对角线互相平分
(B)有一个角是直角的四边形是矩形
(C)矩形的对角线相等
(D)有一个角是直角的平行四边形叫做矩形
2、下面性质中,矩形不一定具有的是 ( ).
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
B
D
随堂练习,巩固深化:
3、直角三角形ABC中,D是斜边的中点,AB=10,则CD=__________.
(3) (4)
4、矩形的两条对角线的夹角为60°,对角线长为15cm,则矩形较短边的长为_____.
5
7.5cm
5.如图:矩形ABCD的两条对角线相交于点O, CE ∥ BD交AB的延长线于点E,
求证:AC=CE.
证明:∵四边形ABCD是矩形,
∴AC=______(矩形对角线_______)
AE ∥ ______ (平行四边形对边_______)
又∵ CE ∥ BD(已知)
∴四边形BECD是________________(定义)
∴BD=_______(平行四边形对边_______)
∴___________(等量代换)
BD
相等
DC
平行
平行四边形
CE
相等
AC=CE
谈一谈,你这节课学到了什么?
1. 平行四边形具有哪些性质?
平行四边形对边平行且相等。
平行四边形对角相等,邻角互补。
平行四边形的对角线互相平分。
边
角
对角线
3.在推动平行四边形的变化过程中,你有没有
发现一种熟悉的、更特殊的图形?
2. 我们都知道三角形具有稳定性,
平行四边形是否也具有稳定性?
18.2.1 矩形(1)
18.2 特殊的平行四边形
2
学导目标 :
会初步运用矩形的概念和性质来解决有关问题.
掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
1
有一个角是直角的平行四边形叫做矩形。
有一个直角
平行四边形
矩形
矩形是一种特殊的平行四边形。
思考: 作为特殊的平行四边形,矩形具有平行四边形的所有性质外,还有哪些特殊性质呢?
1:矩形的四个角都是直角.
2:矩形的对角线相等.
A
B
C
D
3:矩形是轴对称图形。
1:矩形的四个角都是直角
D
C
B
A
命题
性质
几何语言:
∵四边形ABCD是矩形
∴ ∠A=∠B =∠C=∠D =90 °
已知:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
∵四边形ABCD是矩形
∴AB=DC(平行四边形对边相等)
∠ABC=∠DCB(矩形四个角都是直角)
又∵BC=BC
∴ Rt△ABC≌Rt△DCB(SAS) ∴ AC = BD
矩形的对角线相等.
命题2
性质2:
证明:
几何语言:
∵四边形ABCD是矩形
∴ AC = BD
理一理!! 矩形的所有性质:
B
C
D
A
从边看
从角看
从对角线看
从对称性看
对边分别平行且相等
对角相等,邻角互补,四个角都是直角
对角线相等且互相平分。
是轴对称图形
你在矩形中还发现了哪些基本图形?
A
B
C
D
O
A
B
C
D
O
◆ 四个全等的直角三角形.
A
B
C
D
O
◆ 四个等腰三角形.
矩形的对角线相等且互相平分.
性质2:
几何语言:
∵四边形ABCD是矩形
∴ AC = BD ,
OA=OB=OC=OD= AC= BD
O
A
B
D
C
O
C
D
B
A
┛
在Rt△ABC中,BO是斜边AC的中线
直角三角形的性质 :
直角三角形斜边上的中线等于斜边的一半。
则有:BO= AC
试试:用文字叙述
直角三角形的性质
思考:在Rt△ABC中,BO和AC是什么关系
矩形的定义中有两个条件:
一是 , 二是 .
挑战第一关--定义
有一个角是直角
平行四边形
挑战第二关--性质
1、矩形具有而一般平行四边形不具有的性质 ( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
2、如图,四边形ABCD是矩形,若AC=10,则BD=____
C
10
挑战第二关—性质
3、如图,已知Rt△ABC,∠ACB=900,CD是斜边AB上的中线,若CD=6,则AB=____
6
4、矩形是轴对称图形吗 几条对称轴?
12
7、研读课文p53例1,完成学导案例1
例1 如图,矩形ABCD的对角线AC、BD相
交于点O, ∠AOB= 60°,AB=4 ,求矩形对
角线的长.
矩形性质的运用
O
A
B
D
C
解:∵四边形ABCD是矩形,
∴OA=OB( )
又∠AOB= 60°,
∴△OAB是 三角形.
∴OA= .
∴AC=BD=2 = .
等边
AB=4
AB
2×4=8
矩形对角线相等且互相平分
挑战第三关---展示书写
已知:如图,四边形ABCD为矩形,∠AOB=60°,
BD=6.求AB、AD.
60°
随堂练习,巩固深化:
1、下列说法错误的是( ).
(A)矩形的对角线互相平分
(B)有一个角是直角的四边形是矩形
(C)矩形的对角线相等
(D)有一个角是直角的平行四边形叫做矩形
2、下面性质中,矩形不一定具有的是 ( ).
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
B
D
随堂练习,巩固深化:
3、直角三角形ABC中,D是斜边的中点,AB=10,则CD=__________.
(3) (4)
4、矩形的两条对角线的夹角为60°,对角线长为15cm,则矩形较短边的长为_____.
5
7.5cm
5.如图:矩形ABCD的两条对角线相交于点O, CE ∥ BD交AB的延长线于点E,
求证:AC=CE.
证明:∵四边形ABCD是矩形,
∴AC=______(矩形对角线_______)
AE ∥ ______ (平行四边形对边_______)
又∵ CE ∥ BD(已知)
∴四边形BECD是________________(定义)
∴BD=_______(平行四边形对边_______)
∴___________(等量代换)
BD
相等
DC
平行
平行四边形
CE
相等
AC=CE
谈一谈,你这节课学到了什么?
