人教A版选择性必修一 3.1.1椭圆及其标准方程(18张PPT)
文档属性
| 名称 | 人教A版选择性必修一 3.1.1椭圆及其标准方程(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 21:59:57 | ||
图片预览




文档简介
3.1.1椭圆及其标准方程
生产、生活中的圆锥曲线
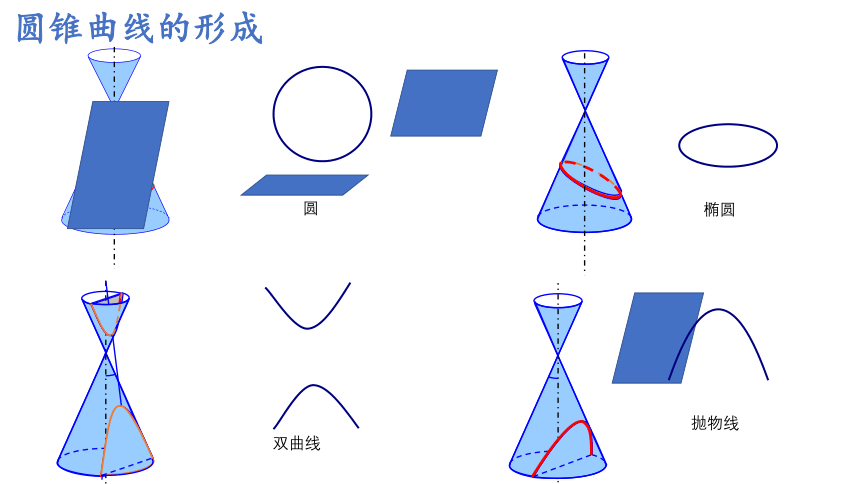
圆锥曲线的形成
双曲线
抛物线
圆
椭圆
圆锥曲线的历史及发展
公元前5世纪,古希腊巧辩学派的数学家提出了几何中三大不可能尺规作图问题:化圆为方问题、立方倍积问题、三等分任意角问题.
公元前4世纪,古希腊数学家梅内克缪斯在研究“立方倍积”问题过程中,发现用不同角度的平面截圆锥面,可以得到不同的曲线,这是圆锥曲线的雏形.
公元前3世纪,古希腊数学家阿波罗尼奥斯在著作《圆锥曲线论》中将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.
1637年,笛卡尔发明了现代数学的基础工具之一——坐标系,将几何和代数相结合,创立了解析几何学,推动了圆锥曲线的发展.
探求椭圆的定义
动手试验:
(1)取一根定长的细绳;
(2)把它的两端用图钉固定在A4纸上;
(3)当两图钉之间的距离小于绳长,用笔尖将绳子拉直,使笔尖在A4纸上慢慢移动,画出一个图形.
探求椭圆的定义
动画演示:
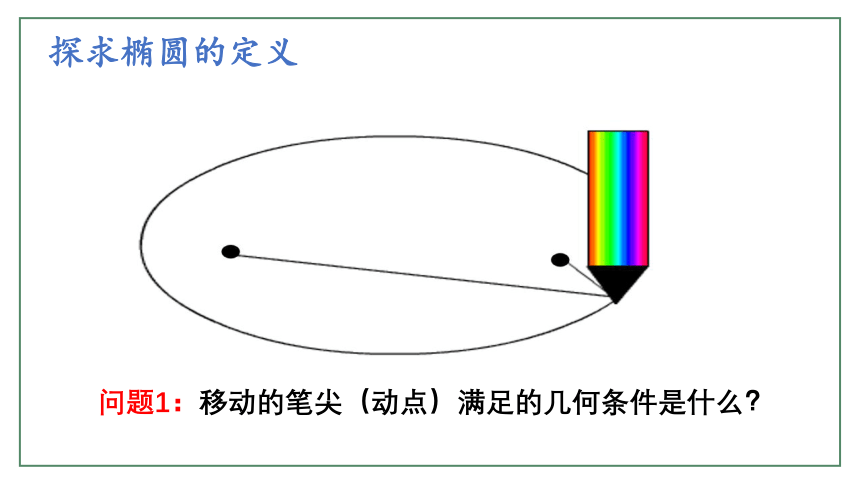
探求椭圆的定义
问题1:移动的笔尖(动点)满足的几何条件是什么?
椭圆的定义
椭圆的定义:
平面内到两个定点F1、F2的距离的和等于常数(大于|F1F2 |)的点M的轨迹叫椭圆. 定点F1、F2叫做椭圆的焦点. 两焦点之间的距离叫做焦距.
问题3: 平面内动点到两个定点F1、F2的距离的和等于|F1F2|,动点的轨迹是什么?
问题4:平面内动点到两个定点F1、F2的距离的和小于|F1F2|,动点的轨迹是什么?
问题5:椭圆上任意一点M,满足的几何条件是什么?
F1
F2
M
常记作2c
线段
不存在
常记作
问题2: 与c的大小关系是什么?
探究椭圆的方程
问题6:直线的点斜式方程、圆的标准方程是用方法推导出来的?
问题7:用坐标法求轨迹方程分为几步?
问题8:你准备如何建立平面直角坐标系?
坐标法
建系、设点、列式、化简、证明
以F1F2所在直线为x轴,以线段F1F2的垂直平分线为y轴,建立平面直角坐标系.
问题9:焦点F1、F2的坐标是什么?
探求椭圆的方程
问题10:椭圆的轨迹条件为什么吗?
|MF1|+|MF2|=2a
问题11:依据轨迹条件列出的方程是什么?
探求椭圆的方程
问题12:如何化简方程 ?
移项得:
两边平方得:
整理得:
两边平方得:
整理得:
因为
两边同除以
得
方程变为:
令b>0,b2=a2-c2
问题14:a与b的大小关系是什么?
问题13: 不等于0成立吗?
椭圆的标准方程
问题15:你能在图中找到表示a,b, 的线段吗?
椭圆的标准方程
x
y
F1
F2
P
O
以F1F2所在直线为y轴,以线段F1F2的垂直平分线为x轴,建立平面直角坐标系。
【问题16】如果焦点在y轴上,椭圆的标准方程怎么推导?
哪个分母大,焦点就在哪个轴上
图 形
焦点坐标
定 义
a、b、c 关系
焦点位置判断
x
y
F1
F2
P
O
x
y
F1
F2
P
O
标准方程
平面内到两个定点的距离之和为常数(大于|F1F2|)的点的轨迹是椭圆.
问题17:根据表格比较两种标准方程结构之间的异同?
学以致用
总结升华
请谈一下,通过本节课有什么收获?
课后作业
一、必做作业
1、思考利用两次平方法化简椭圆的标准方程,每一步变形都是同解变形吗?
2、课本P109页 第3题 、第4题
二、选做作业
1、思考:还有化简椭圆标准方程的其他方法吗?
2、阅读课本116页:用信息技术探究点的轨迹:椭圆.
谢
谢
观
看
生产、生活中的圆锥曲线
圆锥曲线的形成
双曲线
抛物线
圆
椭圆
圆锥曲线的历史及发展
公元前5世纪,古希腊巧辩学派的数学家提出了几何中三大不可能尺规作图问题:化圆为方问题、立方倍积问题、三等分任意角问题.
公元前4世纪,古希腊数学家梅内克缪斯在研究“立方倍积”问题过程中,发现用不同角度的平面截圆锥面,可以得到不同的曲线,这是圆锥曲线的雏形.
公元前3世纪,古希腊数学家阿波罗尼奥斯在著作《圆锥曲线论》中将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.
1637年,笛卡尔发明了现代数学的基础工具之一——坐标系,将几何和代数相结合,创立了解析几何学,推动了圆锥曲线的发展.
探求椭圆的定义
动手试验:
(1)取一根定长的细绳;
(2)把它的两端用图钉固定在A4纸上;
(3)当两图钉之间的距离小于绳长,用笔尖将绳子拉直,使笔尖在A4纸上慢慢移动,画出一个图形.
探求椭圆的定义
动画演示:
探求椭圆的定义
问题1:移动的笔尖(动点)满足的几何条件是什么?
椭圆的定义
椭圆的定义:
平面内到两个定点F1、F2的距离的和等于常数(大于|F1F2 |)的点M的轨迹叫椭圆. 定点F1、F2叫做椭圆的焦点. 两焦点之间的距离叫做焦距.
问题3: 平面内动点到两个定点F1、F2的距离的和等于|F1F2|,动点的轨迹是什么?
问题4:平面内动点到两个定点F1、F2的距离的和小于|F1F2|,动点的轨迹是什么?
问题5:椭圆上任意一点M,满足的几何条件是什么?
F1
F2
M
常记作2c
线段
不存在
常记作
问题2: 与c的大小关系是什么?
探究椭圆的方程
问题6:直线的点斜式方程、圆的标准方程是用方法推导出来的?
问题7:用坐标法求轨迹方程分为几步?
问题8:你准备如何建立平面直角坐标系?
坐标法
建系、设点、列式、化简、证明
以F1F2所在直线为x轴,以线段F1F2的垂直平分线为y轴,建立平面直角坐标系.
问题9:焦点F1、F2的坐标是什么?
探求椭圆的方程
问题10:椭圆的轨迹条件为什么吗?
|MF1|+|MF2|=2a
问题11:依据轨迹条件列出的方程是什么?
探求椭圆的方程
问题12:如何化简方程 ?
移项得:
两边平方得:
整理得:
两边平方得:
整理得:
因为
两边同除以
得
方程变为:
令b>0,b2=a2-c2
问题14:a与b的大小关系是什么?
问题13: 不等于0成立吗?
椭圆的标准方程
问题15:你能在图中找到表示a,b, 的线段吗?
椭圆的标准方程
x
y
F1
F2
P
O
以F1F2所在直线为y轴,以线段F1F2的垂直平分线为x轴,建立平面直角坐标系。
【问题16】如果焦点在y轴上,椭圆的标准方程怎么推导?
哪个分母大,焦点就在哪个轴上
图 形
焦点坐标
定 义
a、b、c 关系
焦点位置判断
x
y
F1
F2
P
O
x
y
F1
F2
P
O
标准方程
平面内到两个定点的距离之和为常数(大于|F1F2|)的点的轨迹是椭圆.
问题17:根据表格比较两种标准方程结构之间的异同?
学以致用
总结升华
请谈一下,通过本节课有什么收获?
课后作业
一、必做作业
1、思考利用两次平方法化简椭圆的标准方程,每一步变形都是同解变形吗?
2、课本P109页 第3题 、第4题
二、选做作业
1、思考:还有化简椭圆标准方程的其他方法吗?
2、阅读课本116页:用信息技术探究点的轨迹:椭圆.
谢
谢
观
看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
