人教A版选择性必修一 3.1.1椭圆及其标准方程 Word教案
文档属性
| 名称 | 人教A版选择性必修一 3.1.1椭圆及其标准方程 Word教案 |  | |
| 格式 | doc | ||
| 文件大小 | 83.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 22:00:52 | ||
图片预览

文档简介
教学设计
教学目标 了解圆锥曲线的背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用.
经历从具体情境中抽象出椭圆的过程,掌握椭圆的定义、标准方程及简单的几何性质.
通过圆锥曲线的学习,进一步体会数形结合的思想.
了解椭圆、抛物线的简单应用.
教学环节 问题或任务 师生活动 设计意图
回顾历史
构
建框架
【任务1】用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.如果改变截面与圆锥的轴所成的角,会得到怎样的截口曲线呢?
【任务2】回顾圆锥曲线发展的历史,从公元前5世纪三大不可能尺规作图问题,到公元前4世纪,梅内克缪斯提出圆锥曲线的雏形,公元前3世纪,阿波罗尼奥斯的著作《圆锥曲线论》,17世纪笛卡尔发明坐标系,创立解析几何学.大家回顾用坐标法研究圆与直线的过程,猜想一下用坐标法研究圆锥曲线的大致思路? 教师1:圆锥曲线与科研、生产以及人类生活有密切联系.如行星绕太阳运行的轨道是椭圆,发电厂冷却塔的外形是双曲线,探照灯反射镜面、卫星接收天线是抛物线绕其对称轴旋转成的抛物面.圆锥曲线有如此广泛的应用,与它的几何特征和几何性质有关,这也正是我们本章要研究的内容.提出任务1,如图用不同角度的平面截圆锥面,我们得到的曲线分别是椭圆、双曲线和抛物线.我们通常把椭圆、抛物线、双曲线统称为圆锥曲线.
学生1:观看思考任务1.
教师2:展示圆锥曲线的历史及发展;提出任务2.
学生2:思考任务2.
【任务1】:重在引发学生思考,并不要求学生解决,这个环节的教学目的是明确本章的意义和价值,促进学生形成积极探究的心理倾向;
【任务2】:让学生从整体上把握本章的学习内容与基本框架,生化学生对坐标法研究问题的基本思路与基本方法的理解.
小组合作
探究定义 【实验探究】取一条定长的细绳,若把细绳两端拉开一段距离,分别固定在图板的两点处,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
【问题1】移动的笔尖(动点)满足的轨迹条件是什么?
【问题2】a和c的大小关系是什么?
【问题3】如果平面内到两定点F1、F2的距离之和等于|F1F2|,那么动点的轨迹是什么?
【问题4】如果平面内到两定点F1、F2的距离之和小于|F1F2|,那么动点的轨迹是什么?
【问题5】对于椭圆上任意一点M,|MF1|、|MF2|满足的关系是什么?
教师3:指导学生按照实验步骤完成【探究试验】.
学生4:小组合作,完成探究试验;
教师4:展示小组活动成果,并进行动画演示,提出问题1.
学生4:思考回到,笔尖到两个定点的距离之和等于定长.
教师5:引导学生用数学语言总结椭圆的定义.
学生5:平面内到两个定点的距离之和等于常数(大于|F1F2|)的动点的轨迹是椭圆.
教师6:提出问题2
学生6:思考问题2,根据椭圆的定义进行回答;
教师7:提出问题【3】、【4】.
学生7:根据实验过程及动画演示进行回答.
教师8:提出问题【5】
学生8:根基椭圆的定义回答问题【5】 由实际操作,强化学生对椭圆的几何特征的认识,提高学生思维的严谨性与语言表达能力,让学生获得焦点、焦距的概念,并将椭圆定义的自然语言转化为符号语言.
合理建系
推导方程 【问题6】我们用什么方法建立直线的点斜式方程与圆的标准方程?
【问题7】坐标法的步骤是什么?
【问题8】我们该如何建立平面直角坐标系?
【问题9】我们需要设出那些点的坐标?
【问题10】根据椭圆的什么轨迹条件列式?
【问题11】列出的式子是什么?
【问题12】如何化简该式?
【问题13】a2(a2-c2)≠0成立吗?
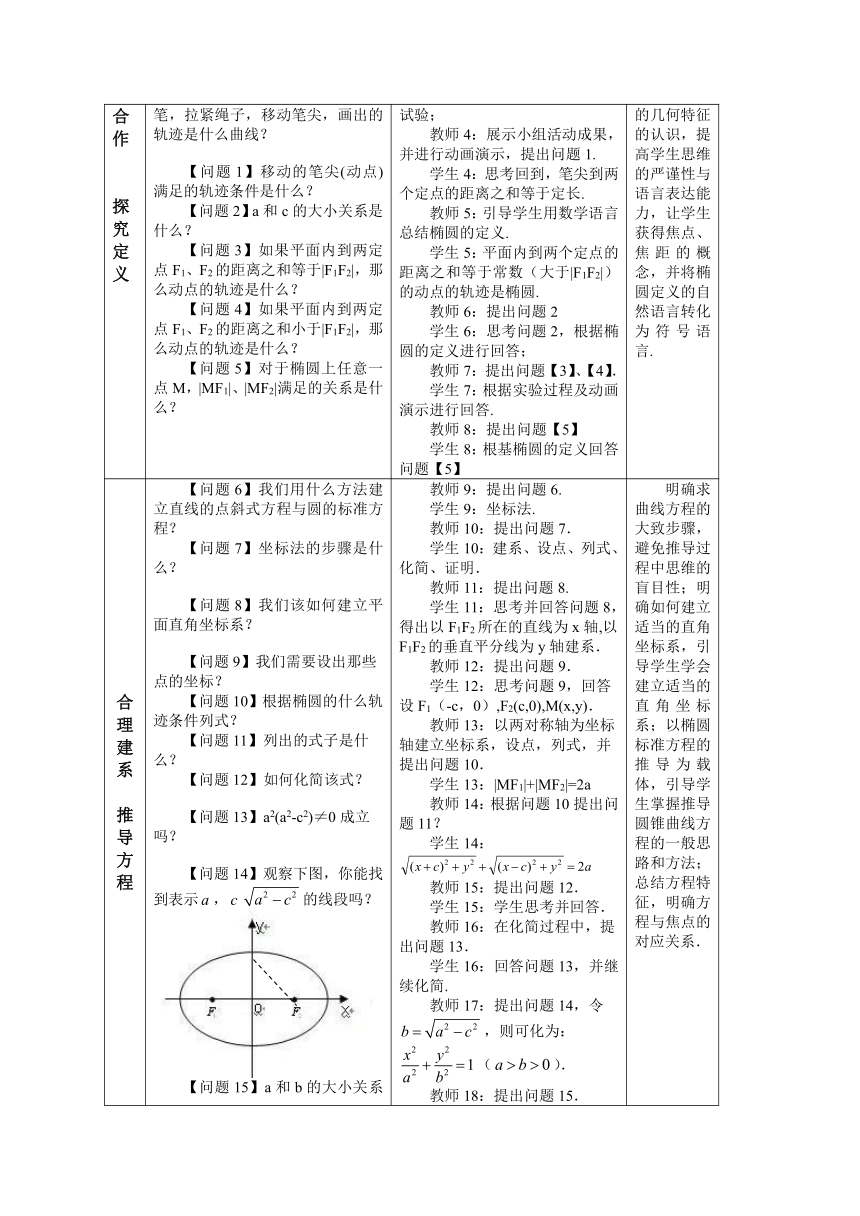
【问题14】观察下图,你能找到表示,的线段吗?
【问题15】a和b的大小关系是什么?
【问题16】如果焦点在y轴上,椭圆的标准方程怎么推导?
【问题17】根据表格,对比椭圆两种方程的结构特点? 教师9:提出问题6.
学生9:坐标法.
教师10:提出问题7.
学生10:建系、设点、列式、化简、证明.
教师11:提出问题8.
学生11:思考并回答问题8,得出以F1F2所在的直线为x轴,以F1F2的垂直平分线为y轴建系.
教师12:提出问题9.
学生12:思考问题9,回答设F1(-c,0),F2(c,0),M(x,y).
教师13:以两对称轴为坐标轴建立坐标系,设点,列式,并提出问题10.
学生13:|MF1|+|MF2|=2a
教师14:根据问题10提出问题11?
学生14:
教师15:提出问题12.
学生15:学生思考并回答.
教师16:在化简过程中,提出问题13.
学生16:回答问题13,并继续化简.
教师17:提出问题14,令,则可化为:().
教师18:提出问题15.
学生17:根据化简过程,回答问题15.
教师19:板书椭圆的标准方程,指出焦点位置及其坐标,以及a,b,c之间的关系.
教师20:提出问题16
学生18:思考回答问题16.
教师21:结合焦点在x轴上椭圆的推导过程,解释椭圆两种标准方程的异同,并板书.
教师22:给出椭圆两种方程的表格,提出问题17.
学生19:学生思考回答.
教师23:展示答案. 明确求曲线方程的大致步骤,避免推导过程中思维的盲目性;明确如何建立适当的直角坐标系,引导学生学会建立适当的直角坐标系;以椭圆标准方程的推导为载体,引导学生掌握推导圆锥曲线方程的一般思路和方法;总结方程特征,明确方程与焦点的对应关系.
随堂练习
学以致用 1、P109练习1.
2、P109练习2.
3、例三:已知椭圆的两个焦点坐标分别是,,并且经过点,求它的标准方程. 教师24:布置课堂例题1、2、3.
学生20:完成课堂例题1、2、3.
教师25:讲解3.
方法一:定义法
方法二:待定系数法
检验学生对椭圆定义、椭圆标准方程的理解与应用.
归纳小结
总结收获 1.椭圆的定义,焦点、焦距的概念;
2.椭圆的两种标准方程:()
(). 师生共同完成. 总结学习要点.
课后练习
巩固提升 一、必做作业
1、思考利用两次平方法化简椭圆的标准方程,每一步变形都是同解变形吗?
2、课本P109页 第3题 、第4题
二、选做作业
1、思考:还有化简椭圆标准方程的其他方法吗?
2、阅读课本116页:用信息技术探究点的轨迹:椭圆.
学生课后进行思考,并完成课后练习. 1、检验是否掌握椭圆的定义及标准方程,思考证明过程中的变形是等价变形;2、为了开拓学生的视野以及培养学生研究问题的能力,让学生查找椭圆标准方程的其它化简方法.3、让学生了解用信息技术解决问题的思路与方法.
教学目标 了解圆锥曲线的背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用.
经历从具体情境中抽象出椭圆的过程,掌握椭圆的定义、标准方程及简单的几何性质.
通过圆锥曲线的学习,进一步体会数形结合的思想.
了解椭圆、抛物线的简单应用.
教学环节 问题或任务 师生活动 设计意图
回顾历史
构
建框架
【任务1】用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.如果改变截面与圆锥的轴所成的角,会得到怎样的截口曲线呢?
【任务2】回顾圆锥曲线发展的历史,从公元前5世纪三大不可能尺规作图问题,到公元前4世纪,梅内克缪斯提出圆锥曲线的雏形,公元前3世纪,阿波罗尼奥斯的著作《圆锥曲线论》,17世纪笛卡尔发明坐标系,创立解析几何学.大家回顾用坐标法研究圆与直线的过程,猜想一下用坐标法研究圆锥曲线的大致思路? 教师1:圆锥曲线与科研、生产以及人类生活有密切联系.如行星绕太阳运行的轨道是椭圆,发电厂冷却塔的外形是双曲线,探照灯反射镜面、卫星接收天线是抛物线绕其对称轴旋转成的抛物面.圆锥曲线有如此广泛的应用,与它的几何特征和几何性质有关,这也正是我们本章要研究的内容.提出任务1,如图用不同角度的平面截圆锥面,我们得到的曲线分别是椭圆、双曲线和抛物线.我们通常把椭圆、抛物线、双曲线统称为圆锥曲线.
学生1:观看思考任务1.
教师2:展示圆锥曲线的历史及发展;提出任务2.
学生2:思考任务2.
【任务1】:重在引发学生思考,并不要求学生解决,这个环节的教学目的是明确本章的意义和价值,促进学生形成积极探究的心理倾向;
【任务2】:让学生从整体上把握本章的学习内容与基本框架,生化学生对坐标法研究问题的基本思路与基本方法的理解.
小组合作
探究定义 【实验探究】取一条定长的细绳,若把细绳两端拉开一段距离,分别固定在图板的两点处,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
【问题1】移动的笔尖(动点)满足的轨迹条件是什么?
【问题2】a和c的大小关系是什么?
【问题3】如果平面内到两定点F1、F2的距离之和等于|F1F2|,那么动点的轨迹是什么?
【问题4】如果平面内到两定点F1、F2的距离之和小于|F1F2|,那么动点的轨迹是什么?
【问题5】对于椭圆上任意一点M,|MF1|、|MF2|满足的关系是什么?
教师3:指导学生按照实验步骤完成【探究试验】.
学生4:小组合作,完成探究试验;
教师4:展示小组活动成果,并进行动画演示,提出问题1.
学生4:思考回到,笔尖到两个定点的距离之和等于定长.
教师5:引导学生用数学语言总结椭圆的定义.
学生5:平面内到两个定点的距离之和等于常数(大于|F1F2|)的动点的轨迹是椭圆.
教师6:提出问题2
学生6:思考问题2,根据椭圆的定义进行回答;
教师7:提出问题【3】、【4】.
学生7:根据实验过程及动画演示进行回答.
教师8:提出问题【5】
学生8:根基椭圆的定义回答问题【5】 由实际操作,强化学生对椭圆的几何特征的认识,提高学生思维的严谨性与语言表达能力,让学生获得焦点、焦距的概念,并将椭圆定义的自然语言转化为符号语言.
合理建系
推导方程 【问题6】我们用什么方法建立直线的点斜式方程与圆的标准方程?
【问题7】坐标法的步骤是什么?
【问题8】我们该如何建立平面直角坐标系?
【问题9】我们需要设出那些点的坐标?
【问题10】根据椭圆的什么轨迹条件列式?
【问题11】列出的式子是什么?
【问题12】如何化简该式?
【问题13】a2(a2-c2)≠0成立吗?
【问题14】观察下图,你能找到表示,的线段吗?
【问题15】a和b的大小关系是什么?
【问题16】如果焦点在y轴上,椭圆的标准方程怎么推导?
【问题17】根据表格,对比椭圆两种方程的结构特点? 教师9:提出问题6.
学生9:坐标法.
教师10:提出问题7.
学生10:建系、设点、列式、化简、证明.
教师11:提出问题8.
学生11:思考并回答问题8,得出以F1F2所在的直线为x轴,以F1F2的垂直平分线为y轴建系.
教师12:提出问题9.
学生12:思考问题9,回答设F1(-c,0),F2(c,0),M(x,y).
教师13:以两对称轴为坐标轴建立坐标系,设点,列式,并提出问题10.
学生13:|MF1|+|MF2|=2a
教师14:根据问题10提出问题11?
学生14:
教师15:提出问题12.
学生15:学生思考并回答.
教师16:在化简过程中,提出问题13.
学生16:回答问题13,并继续化简.
教师17:提出问题14,令,则可化为:().
教师18:提出问题15.
学生17:根据化简过程,回答问题15.
教师19:板书椭圆的标准方程,指出焦点位置及其坐标,以及a,b,c之间的关系.
教师20:提出问题16
学生18:思考回答问题16.
教师21:结合焦点在x轴上椭圆的推导过程,解释椭圆两种标准方程的异同,并板书.
教师22:给出椭圆两种方程的表格,提出问题17.
学生19:学生思考回答.
教师23:展示答案. 明确求曲线方程的大致步骤,避免推导过程中思维的盲目性;明确如何建立适当的直角坐标系,引导学生学会建立适当的直角坐标系;以椭圆标准方程的推导为载体,引导学生掌握推导圆锥曲线方程的一般思路和方法;总结方程特征,明确方程与焦点的对应关系.
随堂练习
学以致用 1、P109练习1.
2、P109练习2.
3、例三:已知椭圆的两个焦点坐标分别是,,并且经过点,求它的标准方程. 教师24:布置课堂例题1、2、3.
学生20:完成课堂例题1、2、3.
教师25:讲解3.
方法一:定义法
方法二:待定系数法
检验学生对椭圆定义、椭圆标准方程的理解与应用.
归纳小结
总结收获 1.椭圆的定义,焦点、焦距的概念;
2.椭圆的两种标准方程:()
(). 师生共同完成. 总结学习要点.
课后练习
巩固提升 一、必做作业
1、思考利用两次平方法化简椭圆的标准方程,每一步变形都是同解变形吗?
2、课本P109页 第3题 、第4题
二、选做作业
1、思考:还有化简椭圆标准方程的其他方法吗?
2、阅读课本116页:用信息技术探究点的轨迹:椭圆.
学生课后进行思考,并完成课后练习. 1、检验是否掌握椭圆的定义及标准方程,思考证明过程中的变形是等价变形;2、为了开拓学生的视野以及培养学生研究问题的能力,让学生查找椭圆标准方程的其它化简方法.3、让学生了解用信息技术解决问题的思路与方法.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
