广东省执信中学2011-2012学年高二上学期期末考试试题(数学文)
文档属性
| 名称 | 广东省执信中学2011-2012学年高二上学期期末考试试题(数学文) |
|
|
| 格式 | zip | ||
| 文件大小 | 294.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-08 00:00:00 | ||
图片预览




文档简介
广东省执信中学2011-2012学年高二上学期期末考试试题(数学文)
第一部分 选择题 (共50分)
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,那么集合 等于( * )
A. B. C. D.
2.若函数是函数的反函数,且,则( * )
A. B. C. D.
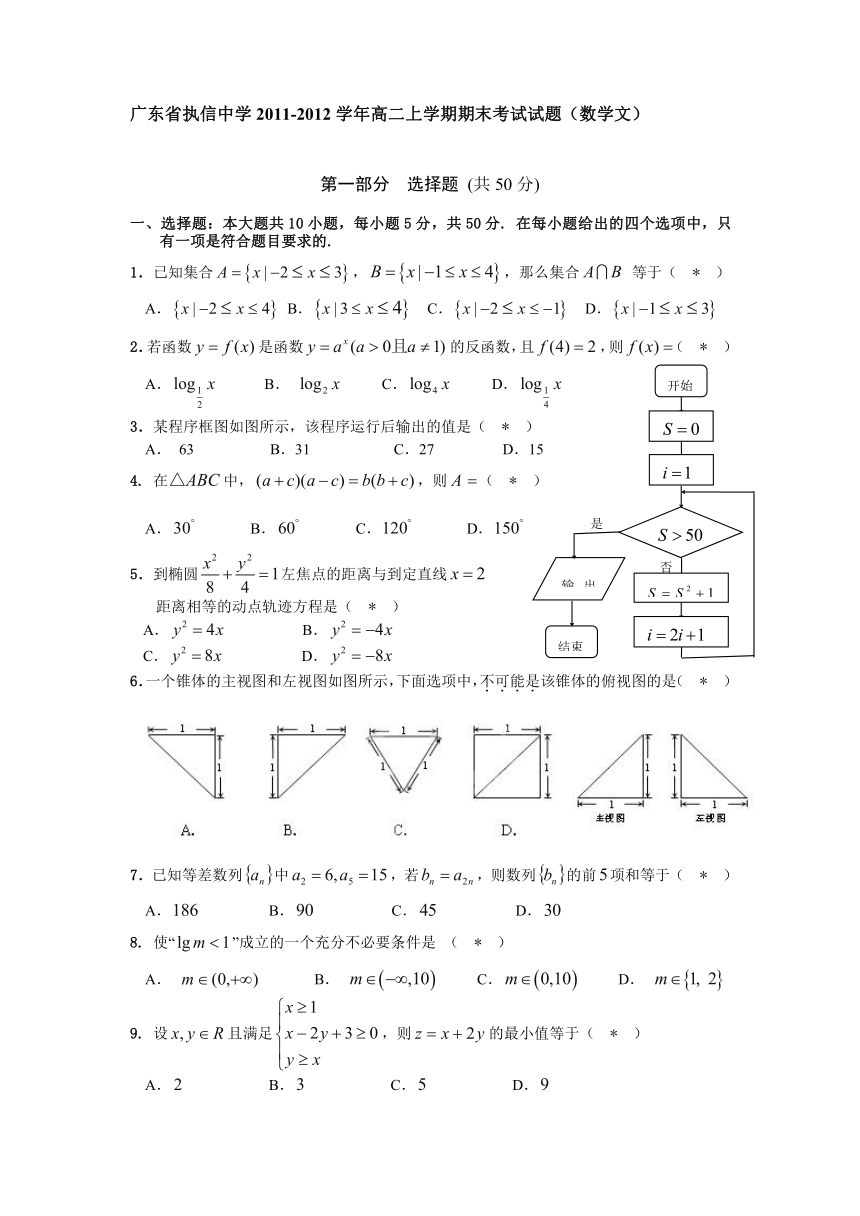
3.某程序框图如图所示,该程序运行后输出的值是( * )
A. 63 B.31 C.27 D.15
4. 在中,,则( * )
A. B. C. D.
5.到椭圆左焦点的距离与到定直线
距离相等的动点轨迹方程是( * )
A. B.
C. D.
6.一个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是( * )
7.已知等差数列中,若,则数列的前项和等于( * )
A. B. C. D.
8. 使“”成立的一个充分不必要条件是 ( * )
A. B. C. D.
9. 设且满足,则的最小值等于( * )
A. B. C. D.
10.若函数满足且时,,
函数,则函数在区间内的零点的
个数为( * )
A. B. C. D.
第二部分 非选择题 (共100分)
二、填空题:本大题共4小题,每小题5分,共20分.
11. 命题“”的否定是:___***_____;
12. 平面向量、的夹角为,,, 则___***_____;
13. 已知圆的圆心为,直线与圆相交于两点,且,则圆的方程为___***_____;
14. 已知双曲线的顶点与焦点分别是椭圆的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为___***_____ .
三、解答题:本大题共6小题,共 80 分. 解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分12分)
已知函数.
(Ⅰ)求函数的最小正周期;
(Ⅱ)求函数的单调递增区间.
16. (本小题满分12分)
某车间将名技工平均分为甲、乙两组加工某种零件,在单位时间内每个技工加工零件
若干,其中合格零件的个数如下表:
1号 2号 3号 4号 5号
甲组 4 5 7 9 10
乙组 5 6 7 8 9
(Ⅰ)分别求出甲、乙两组技工在单位时间内完成合格零件的平均数及方差,并由此比较两组技工的技术水平;
(Ⅱ)质检部门从该车间甲、乙两组中各随机抽取名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过件,则称该车间“质量合格”,求该车间“质量合格”的概率.
18. (本小题满分14分)
已知椭圆的方程为:,其中,直线与椭圆的交点在轴上的射影恰为椭圆的焦点.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线与椭圆在轴上方的一个交点为,是椭圆的右焦点,试探究以为直径的圆与以椭圆长轴为直径的圆的位置关系.
19. (本小题满分14分)
已知函数定义域为且同时满足: ①图像向左平移1个单位后所得函数为偶函数;②对于任意大于1的不等实数,总有成立.
(Ⅰ)的图像是否有对称轴?如果有,写出对称轴方程,并说明在区间上的单调性;
(Ⅱ)设,如果,判断是否有负实根并说明理由;
(Ⅲ)如果且,比较与的大小并说明理由.
20.(本小题满分14分)
已知数列的前项和,函数对任意的都有,数列满足.
(Ⅰ)分别求数列、的通项公式;
(Ⅱ)若数列满足,是数列的前项和,是否存在正实数,使不等式对于一切的恒成立?若存在请指出的取值范围,并证明;若不存在请说明理由.
参考答案及评分标准
一、选择题:本大题共10小题,每小题5分,共50分.
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A C D C B D B C
二、填空题:本大题共4小题,每小题5分,满分20分.
11. 12. 13. 14.
16. (本小题满分12分)
【解析】(Ⅰ)依题意,
……………………………… 2分
……… 3分
…………… 4分
因为,
所以,两组技工的总体水平相同,甲组技工的技术水平差异比乙组大 …………… 6分
(Ⅱ)记该车间“质量合格”为事件A,则从甲、乙两组中各抽取1名技工完成合格零件个数的基本事件为:(4,5),(4,6),(4,7),(4,8),(4,9),(5,5),(5,6),(5,7),(5,8),(5,9),(7,5),(7,6),(7,7),(7,8),(7,9),(9,5),(9,6),(9,7),(9,8),(9,9),(10,5),(10,6),(10,7),(10,8),(10,9)共25种 ………… 8分
事件A包含的基本事件为:(4,9),(5,8),(5,9),(7,6),(7,7),(7,8),(7,9),
(9,5),(9,6),(9,7),(9,8),(9,9),(10,5),(10,6),(10,7),(10,8),
(10,9)共17种 ……………………………… 10分
所以 ……………………………… 11分
答:该车间“质量合格”的概率为 ……………………………… 12分
17.(本小题满分14分)
【解析】(Ⅰ)证明:方法一:,连结CG,
∵分别为、的中点 ∴且
……………………………… 2分
平面,平面
平面 ……………………………… 4分
方法二: ∵分别为、的中点
∴且 ……………………………… 1分
平面,平面
平面
平面,平面
平面
∴平面平面 ……………………………… 3分
∵平面平面 ……………… 4分(Ⅱ) ∵ ∴ ∴在中 =
∴即……………………… 6分
又∵
∴平面 ∴ ……………………8分
∴平面 …………………… 9分
(Ⅲ) 方法一: ∵平面 ∴
∵ ∴平面
∴为三棱锥的高 …………………… 11分
面,
……………………… 12分
……………………… 14分
方法二: ……………………… 10分
平面 为三棱锥的高 ………………… 11分
面
……………………………… 12分
………………………… 14分
方法三: ……………………… 10分
面 为三棱锥的高 …………………… 11分
平面
………………………… 12分
………………………… 14分
18. (本小题满分14分)
【解析】 (Ⅰ)方法一:设椭圆的左右焦点分别为、,直线与椭圆的一个交点坐标是, ………………………… 2分
根据椭圆的定义得:,
即,即, ………………… 4分
又,,联立三式解得 …………………… 6分
所以椭圆的方程为: ……………………………… 7分
方法二:设椭圆的左右焦点分别为、,直线与椭圆的一个交点坐标是,……………… 2分
将点坐标代入椭圆的方程得
化简整理得 ………………………… 4分
解得或
或 或(此时,舍去)
………………………… 6分
所以椭圆的方程为: ………………………… 7分
(Ⅱ)由(1)可知,直线与椭圆的一个交点为,
则以为直径的圆方程是,圆心为,半径为 …… 9分
以椭圆长轴为直径的圆的方程是,圆心是,半径是 ………… 11分
两圆心距为,所以两圆内切. …………………………… 14分
19、(本小题满分14分)
【解析】(Ⅰ)由条件①得的图像关于直线对称 ……………………… 2分
由条件②得时,恒成立,时,恒成立,
在上单调递增 …………………………… 4分
又的图像关于直线对称,在上单调递减 ……… 5分
(Ⅱ)方法一:若有负根,则,
…………………………… 6分
, 在上单调递减 ……………… 8分
,与矛盾 故无负实根 ………… 10分
方法二:若有负根,则
…………………………… 6分
, 在上单调递减
结合图像如右图所示
………………………… 8分
知与的图象在轴左侧无交点,故无负实根 ……… 10分
(Ⅲ)解:点与点为上关于直线对称的两点
…………………………… 11分
, …………………………… 12分
又在上单调递增, …… 14分
20.(本小题满分14分)
【解析】(Ⅰ) …………………………… 1分
时满足上式,故 ……………………………2分
∵=1∴ ……………………………3分
∵ ①
∴ ②
∴①+②,得 …………………………… 5分
(Ⅱ)∵,∴ ………………………………6分
∴, ①
, ②
①-②得 …………………………8分
即 ………………………… 9分
要使得不等式恒成立,
结束
输出
否
是
开始
第一部分 选择题 (共50分)
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,那么集合 等于( * )
A. B. C. D.
2.若函数是函数的反函数,且,则( * )
A. B. C. D.
3.某程序框图如图所示,该程序运行后输出的值是( * )
A. 63 B.31 C.27 D.15
4. 在中,,则( * )
A. B. C. D.
5.到椭圆左焦点的距离与到定直线
距离相等的动点轨迹方程是( * )
A. B.
C. D.
6.一个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是( * )
7.已知等差数列中,若,则数列的前项和等于( * )
A. B. C. D.
8. 使“”成立的一个充分不必要条件是 ( * )
A. B. C. D.
9. 设且满足,则的最小值等于( * )
A. B. C. D.
10.若函数满足且时,,
函数,则函数在区间内的零点的
个数为( * )
A. B. C. D.
第二部分 非选择题 (共100分)
二、填空题:本大题共4小题,每小题5分,共20分.
11. 命题“”的否定是:___***_____;
12. 平面向量、的夹角为,,, 则___***_____;
13. 已知圆的圆心为,直线与圆相交于两点,且,则圆的方程为___***_____;
14. 已知双曲线的顶点与焦点分别是椭圆的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为___***_____ .
三、解答题:本大题共6小题,共 80 分. 解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分12分)
已知函数.
(Ⅰ)求函数的最小正周期;
(Ⅱ)求函数的单调递增区间.
16. (本小题满分12分)
某车间将名技工平均分为甲、乙两组加工某种零件,在单位时间内每个技工加工零件
若干,其中合格零件的个数如下表:
1号 2号 3号 4号 5号
甲组 4 5 7 9 10
乙组 5 6 7 8 9
(Ⅰ)分别求出甲、乙两组技工在单位时间内完成合格零件的平均数及方差,并由此比较两组技工的技术水平;
(Ⅱ)质检部门从该车间甲、乙两组中各随机抽取名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过件,则称该车间“质量合格”,求该车间“质量合格”的概率.
18. (本小题满分14分)
已知椭圆的方程为:,其中,直线与椭圆的交点在轴上的射影恰为椭圆的焦点.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线与椭圆在轴上方的一个交点为,是椭圆的右焦点,试探究以为直径的圆与以椭圆长轴为直径的圆的位置关系.
19. (本小题满分14分)
已知函数定义域为且同时满足: ①图像向左平移1个单位后所得函数为偶函数;②对于任意大于1的不等实数,总有成立.
(Ⅰ)的图像是否有对称轴?如果有,写出对称轴方程,并说明在区间上的单调性;
(Ⅱ)设,如果,判断是否有负实根并说明理由;
(Ⅲ)如果且,比较与的大小并说明理由.
20.(本小题满分14分)
已知数列的前项和,函数对任意的都有,数列满足.
(Ⅰ)分别求数列、的通项公式;
(Ⅱ)若数列满足,是数列的前项和,是否存在正实数,使不等式对于一切的恒成立?若存在请指出的取值范围,并证明;若不存在请说明理由.
参考答案及评分标准
一、选择题:本大题共10小题,每小题5分,共50分.
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A C D C B D B C
二、填空题:本大题共4小题,每小题5分,满分20分.
11. 12. 13. 14.
16. (本小题满分12分)
【解析】(Ⅰ)依题意,
……………………………… 2分
……… 3分
…………… 4分
因为,
所以,两组技工的总体水平相同,甲组技工的技术水平差异比乙组大 …………… 6分
(Ⅱ)记该车间“质量合格”为事件A,则从甲、乙两组中各抽取1名技工完成合格零件个数的基本事件为:(4,5),(4,6),(4,7),(4,8),(4,9),(5,5),(5,6),(5,7),(5,8),(5,9),(7,5),(7,6),(7,7),(7,8),(7,9),(9,5),(9,6),(9,7),(9,8),(9,9),(10,5),(10,6),(10,7),(10,8),(10,9)共25种 ………… 8分
事件A包含的基本事件为:(4,9),(5,8),(5,9),(7,6),(7,7),(7,8),(7,9),
(9,5),(9,6),(9,7),(9,8),(9,9),(10,5),(10,6),(10,7),(10,8),
(10,9)共17种 ……………………………… 10分
所以 ……………………………… 11分
答:该车间“质量合格”的概率为 ……………………………… 12分
17.(本小题满分14分)
【解析】(Ⅰ)证明:方法一:,连结CG,
∵分别为、的中点 ∴且
……………………………… 2分
平面,平面
平面 ……………………………… 4分
方法二: ∵分别为、的中点
∴且 ……………………………… 1分
平面,平面
平面
平面,平面
平面
∴平面平面 ……………………………… 3分
∵平面平面 ……………… 4分(Ⅱ) ∵ ∴ ∴在中 =
∴即……………………… 6分
又∵
∴平面 ∴ ……………………8分
∴平面 …………………… 9分
(Ⅲ) 方法一: ∵平面 ∴
∵ ∴平面
∴为三棱锥的高 …………………… 11分
面,
……………………… 12分
……………………… 14分
方法二: ……………………… 10分
平面 为三棱锥的高 ………………… 11分
面
……………………………… 12分
………………………… 14分
方法三: ……………………… 10分
面 为三棱锥的高 …………………… 11分
平面
………………………… 12分
………………………… 14分
18. (本小题满分14分)
【解析】 (Ⅰ)方法一:设椭圆的左右焦点分别为、,直线与椭圆的一个交点坐标是, ………………………… 2分
根据椭圆的定义得:,
即,即, ………………… 4分
又,,联立三式解得 …………………… 6分
所以椭圆的方程为: ……………………………… 7分
方法二:设椭圆的左右焦点分别为、,直线与椭圆的一个交点坐标是,……………… 2分
将点坐标代入椭圆的方程得
化简整理得 ………………………… 4分
解得或
或 或(此时,舍去)
………………………… 6分
所以椭圆的方程为: ………………………… 7分
(Ⅱ)由(1)可知,直线与椭圆的一个交点为,
则以为直径的圆方程是,圆心为,半径为 …… 9分
以椭圆长轴为直径的圆的方程是,圆心是,半径是 ………… 11分
两圆心距为,所以两圆内切. …………………………… 14分
19、(本小题满分14分)
【解析】(Ⅰ)由条件①得的图像关于直线对称 ……………………… 2分
由条件②得时,恒成立,时,恒成立,
在上单调递增 …………………………… 4分
又的图像关于直线对称,在上单调递减 ……… 5分
(Ⅱ)方法一:若有负根,则,
…………………………… 6分
, 在上单调递减 ……………… 8分
,与矛盾 故无负实根 ………… 10分
方法二:若有负根,则
…………………………… 6分
, 在上单调递减
结合图像如右图所示
………………………… 8分
知与的图象在轴左侧无交点,故无负实根 ……… 10分
(Ⅲ)解:点与点为上关于直线对称的两点
…………………………… 11分
, …………………………… 12分
又在上单调递增, …… 14分
20.(本小题满分14分)
【解析】(Ⅰ) …………………………… 1分
时满足上式,故 ……………………………2分
∵=1∴ ……………………………3分
∵ ①
∴ ②
∴①+②,得 …………………………… 5分
(Ⅱ)∵,∴ ………………………………6分
∴, ①
, ②
①-②得 …………………………8分
即 ………………………… 9分
要使得不等式恒成立,
结束
输出
否
是
开始
同课章节目录
