19.2.2.2一次函数的图像与性质 课件(共38张PPT)
文档属性
| 名称 | 19.2.2.2一次函数的图像与性质 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 16:06:10 | ||
图片预览







文档简介
19.2.2.2 一次函数的图像与性质
第十九章 一次函数
2021年春人教版八年级(下)数学
你还记得正比例函数的图象和它的性质吗?
新课导入
这节课我们一起来探讨一次函数的图象及它的性质.
(1)会画一次函数的图象,会根据图象(或k的符号)说出一次函数的性质.
(2)知道正比例函数y=kx(k≠0)与一次函数y=kx+b(k≠0)的图象之间的平移关系.
(3)掌握一次函数的图象和性质与k,b的关系.
重点:一次函数的图象和性质.
难点:一次函数图象与性质的运用.
学习目标
一次函数的图象
你还记得我们之前是怎么画函数的图象的吗?
根据函数关系,先列表,再在直角坐标系中描出表中的数对,最后连线.
探究新知
那我们能否也用这样的方法来画一次函数的图象呢?
猜
想
分
析
根据一次函数的表达式y=kx+b(k≠0)可知,一次函数的图象是一条直线,又因为两点可以确定一条直线,所以我们可以用两点法来画一次函数的图象.
例1 画出函数y=2x-1与y=-0.5x+1的图象.
验
证
列表表示当x=0,x=1时两个函数的对应值.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
y=-0.5x+1
-1
1
1
0.5
例题讲解
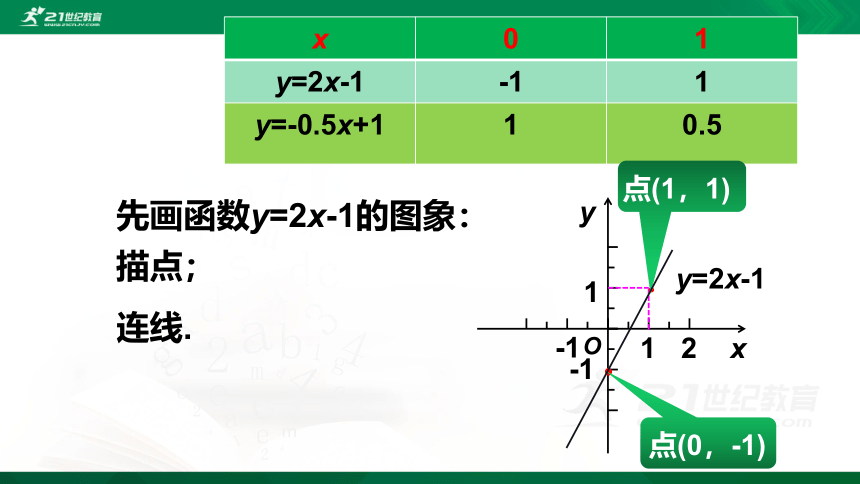
描点;
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
连线.
先画函数y=2x-1的图象:
O
x
y
y=2x-1
1
1
-1
-1
2
点(0,-1)
点(1,1)
描点;
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
连线.
O
x
y
1
1
-1
-1
y=2x-1
y=-0.5x+1
2
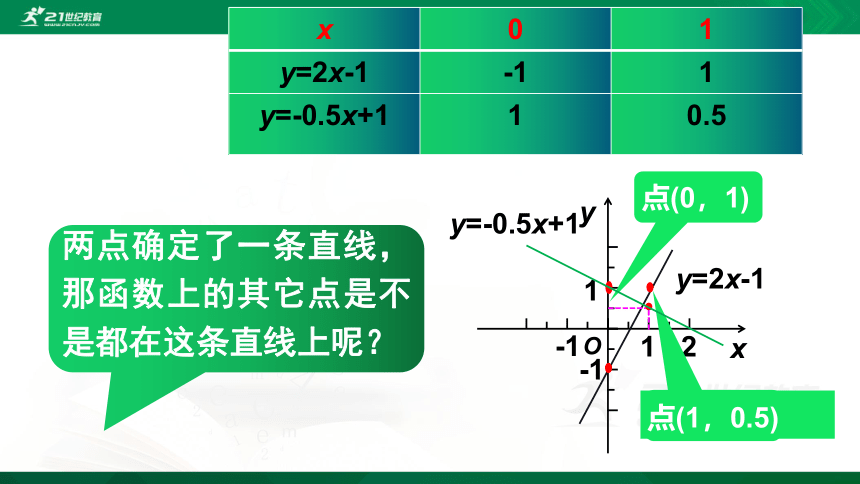
我们用同样的方法也可以画出函数y=-0.5x+1的图象:
点(0,1)
点(1,0.5)
先画函数y=2x-1的图象:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
点(0,1)
点(1,0.5)
两点确定了一条直线,那函数上的其它点是不是都在这条直线上呢?
y=-0.5x+1
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
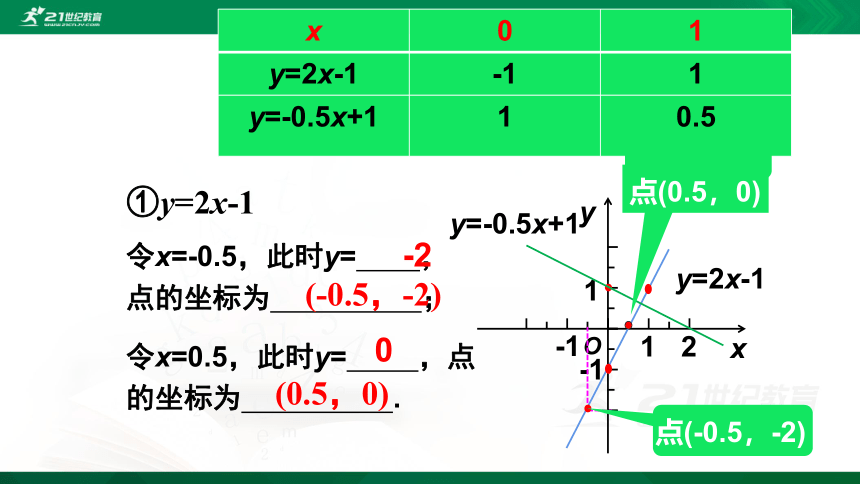
①y=2x-1
令x=-0.5,此时y= ,
点的坐标为 ;
-2
令x=0.5,此时y= ,点的坐标为 .
0
(-0.5,-2)
(0.5,0)
点(0.5,0)
点(-0.5,-2)
y=-0.5x+1
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
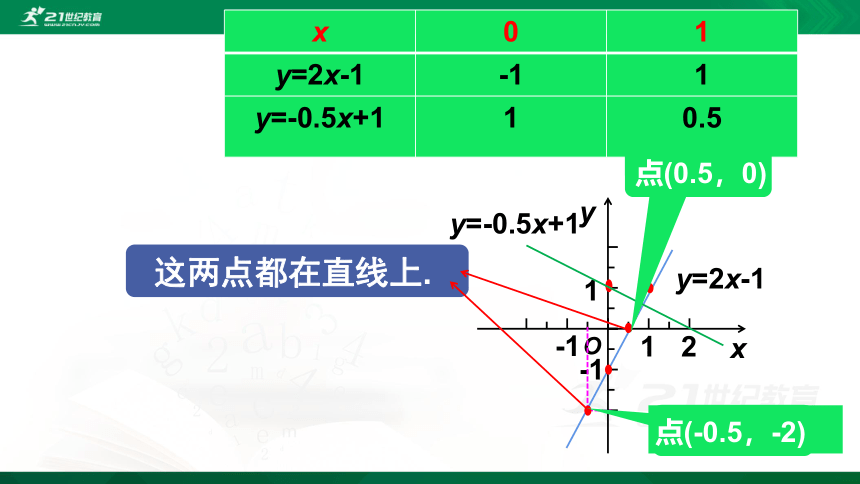
这两点都在直线上.
点(0.5,0)
点(-0.5,-2)
y=-0.5x+1
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
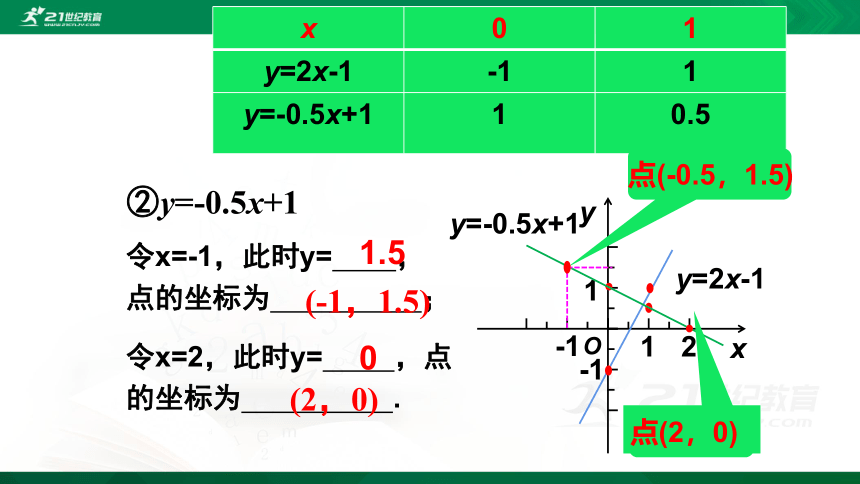
②y=-0.5x+1
令x=-1,此时y= ,
点的坐标为 ;
令x=2,此时y= ,点的坐标为 .
1.5
0
(-1,1.5)
(2,0)
点(-0.5,1.5)
点(2,0)
y=-0.5x+1
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
点(-0.5,1.5)
点(2,0)
这两点都在直线上.
y=-0.5x+1
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
由此我们可以归纳出函数上的其它点也在直线上,所以两点法确定的图象可以表示对应的函数图象.
y=-0.5x+1
除了能用两点法得到一次函数的图象外,你还能想出别的方法吗?
思
考
例2 画出函数y=-6x与y=-6x+5的图象.
分析:函数y=-6x与y=-6x+5中,自变量x可以取任意实数.列表表示几组对应值.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-2
-1
0
1
2
y=-6x
y=-6x+5
12
6
0
-6
-12
17
11
5
-1
-7
例题讲解
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-2
-1
0
1
2
y=-6x
12
6
0
-6
-12
y=-6x+5
17
11
5
-1
-7
①画函数y=-6x的图象
根据前面所学的的两点法作图,我们只需要选择函数y=-6x上的两个坐标点就可以画出相应的函数图象.
选择两个点.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-2
-1
0
1
2
y=-6x
12
6
0
-6
-12
y=-6x+5
17
11
5
-1
-7
O
x
y
①画函数y=-6x的图象
6
3
-3
-6
-3
-6
3
6
描点;
连线.
y=-6x
点(0,0)
点(1,-6)
点(1,1)
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-2
-1
0
1
2
y=-6x
12
6
0
-6
-12
y=-6x+5
17
11
5
-1
-7
O
x
y
y=-6x
①画函数y=-6x的图象
6
3
-3
-6
-3
-6
3
6
②用同样的方法画函数y=-6x+5的图象
描点;
连线.
y=-6x+5
选择两个点.
点(0,5)
思
考
比较右边两个函数图象,你能发现什么?
O
x
y
y=-6x
6
3
-3
-6
-3
-6
3
6
y=-6x+5
(1)这两个函数的图象形状都是 ,并且倾斜程度 .
(2)函数y=-6x的图象经过 ,函数y=-6x+5的图象与y轴交于 ,即它可以看作由直线y=-6x向 平移 个单位长度而得到.
一条直线
相同
原点
(0,5)
O
x
y
y=-6x
6
3
-3
-6
-3
-6
3
6
y=-6x+5
右
5
联系上面的发现,你能归纳出一次函数y=kx+b(k≠0)与正比例函数y=kx(k≠0)之间的关系吗?
直线y=kx+b可以看作由直线y=kx平移|b|个单位长度得到.当b>0时,向上平移;当b<0时,向下平移 .
一次函数图象的画法
2.平移法:直线y=kx+b可以看作由直线y=kx平移|b|个单位长度得到.当b>0时,向上平移;当b<0,向下平移 .
1.两点法:由于两点确定一条直线,所以在平面直角坐标系中画出一次函数的图象时,先描出适合解析式的两点,再通过这两点作直线即可.
归纳小结
探
究
画出函数y=x+1,y=-x+1及y=2x+1 y=-2x+l的图象 .并思考一次函数解析式y=kx+b(k, b是常数,k≠0)中,k、b的正负对函数图象有什么影响?
一次函数的性质
分别画出下面四个函数的图象.
y=x+1
y=-x+1
y=2x+1
y=-2x+l
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}y=kx+b
图象经过的象限
y和x的变化
k>0
b>0
b=0
b<0
k<0
b>0
b=0
b<0
观察图象,填写表格.
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
y随x的增大
而增大
y随x的增大
而减小
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}y=kx+b
图象经过的象限
y和x的变化
k>0
b>0
b=0
b<0
k<0
b>0
b=0
b<0
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
y随x的增大
而增大
y随x的增大
而减小
你能从表格中归纳出一次函数的性质吗?
你能从表格中归纳出一次函数的性质吗?
当k>0时,直线从左向右上升,即y随x的增大而增大.
当k<0时,直线从左向右下降,即y随x的增大而减小.
A
1.一次函数y=x+2的图象大致是( )
A
B
C
D
课堂练习
2.在同一直角坐标系中,对于函数:①y=-x-1,②y=x+1,③y=-x+1,④y=-2x-1的图象,下列说法不正确的是( )
A.通过点(-1,0)的是①和③
B.两直线的交点在y轴负半轴上的是①和④
C.相互平行的是①和③
D.关于y轴对称的是②和③
A
课堂练习
3.已知正比例函数y=(k-3)x,若y随x的增大而增大,则k的取值范围是( )
A.k<0 B.k>0
C.k<3 D.k>3
D
4.若一次函数y=(2m-1)x+3-2m的图象经过第一、二、四象限,则m的取值范围是m< .
课堂练习
5.下列关于一次函数y=-2x+1的说法:
①y随x的增大而减小;
②图象与直线y=-2x平行;
③图象与y轴的交点坐标是(0,1);
④图象经过第一、二、四象限.
其中正确的有 个.
4
课堂练习
6.在平面直角坐标系中画出函数y=-12x+3的图象.
(1)在图象上标出横坐标为-4的点A,并写出它的坐标;
(2)在图象上标出与y轴的距离是2个单位长度的点,并写出它的坐标.
课堂练习
7.一次函数y=(2a+4)x-(3-b),当a,b为何值时:
a>-2,b为任意实数
(2)图象经过第二、三、四象限;
(1)y随x的增大而增大;
a<-2,b<3
课堂练习
7.一次函数y=(2a+4)x-(3-b),当a,b为何值时:
a≠-2,b>3
(4)图象过原点.
(3)图象与y轴的交点在x轴上方;
a≠-2,b=3
课堂练习
1.一次函数图象的画法
平移法
两点法
当k>0时,直线从左向右上升,即y随x的增大而增大.
当k<0时,直线从左向右下降,即y随x的增大而减小.
2.一次函数的性质
课堂小结
https://www.21cnjy.com/help/help_extract.php
第十九章 一次函数
2021年春人教版八年级(下)数学
你还记得正比例函数的图象和它的性质吗?
新课导入
这节课我们一起来探讨一次函数的图象及它的性质.
(1)会画一次函数的图象,会根据图象(或k的符号)说出一次函数的性质.
(2)知道正比例函数y=kx(k≠0)与一次函数y=kx+b(k≠0)的图象之间的平移关系.
(3)掌握一次函数的图象和性质与k,b的关系.
重点:一次函数的图象和性质.
难点:一次函数图象与性质的运用.
学习目标
一次函数的图象
你还记得我们之前是怎么画函数的图象的吗?
根据函数关系,先列表,再在直角坐标系中描出表中的数对,最后连线.
探究新知
那我们能否也用这样的方法来画一次函数的图象呢?
猜
想
分
析
根据一次函数的表达式y=kx+b(k≠0)可知,一次函数的图象是一条直线,又因为两点可以确定一条直线,所以我们可以用两点法来画一次函数的图象.
例1 画出函数y=2x-1与y=-0.5x+1的图象.
验
证
列表表示当x=0,x=1时两个函数的对应值.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
y=-0.5x+1
-1
1
1
0.5
例题讲解
描点;
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
连线.
先画函数y=2x-1的图象:
O
x
y
y=2x-1
1
1
-1
-1
2
点(0,-1)
点(1,1)
描点;
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
连线.
O
x
y
1
1
-1
-1
y=2x-1
y=-0.5x+1
2
我们用同样的方法也可以画出函数y=-0.5x+1的图象:
点(0,1)
点(1,0.5)
先画函数y=2x-1的图象:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
点(0,1)
点(1,0.5)
两点确定了一条直线,那函数上的其它点是不是都在这条直线上呢?
y=-0.5x+1
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
①y=2x-1
令x=-0.5,此时y= ,
点的坐标为 ;
-2
令x=0.5,此时y= ,点的坐标为 .
0
(-0.5,-2)
(0.5,0)
点(0.5,0)
点(-0.5,-2)
y=-0.5x+1
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
这两点都在直线上.
点(0.5,0)
点(-0.5,-2)
y=-0.5x+1
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
②y=-0.5x+1
令x=-1,此时y= ,
点的坐标为 ;
令x=2,此时y= ,点的坐标为 .
1.5
0
(-1,1.5)
(2,0)
点(-0.5,1.5)
点(2,0)
y=-0.5x+1
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
点(-0.5,1.5)
点(2,0)
这两点都在直线上.
y=-0.5x+1
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
1
y=2x-1
-1
1
y=-0.5x+1
1
0.5
O
x
y
1
1
-1
-1
y=2x-1
2
由此我们可以归纳出函数上的其它点也在直线上,所以两点法确定的图象可以表示对应的函数图象.
y=-0.5x+1
除了能用两点法得到一次函数的图象外,你还能想出别的方法吗?
思
考
例2 画出函数y=-6x与y=-6x+5的图象.
分析:函数y=-6x与y=-6x+5中,自变量x可以取任意实数.列表表示几组对应值.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-2
-1
0
1
2
y=-6x
y=-6x+5
12
6
0
-6
-12
17
11
5
-1
-7
例题讲解
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-2
-1
0
1
2
y=-6x
12
6
0
-6
-12
y=-6x+5
17
11
5
-1
-7
①画函数y=-6x的图象
根据前面所学的的两点法作图,我们只需要选择函数y=-6x上的两个坐标点就可以画出相应的函数图象.
选择两个点.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-2
-1
0
1
2
y=-6x
12
6
0
-6
-12
y=-6x+5
17
11
5
-1
-7
O
x
y
①画函数y=-6x的图象
6
3
-3
-6
-3
-6
3
6
描点;
连线.
y=-6x
点(0,0)
点(1,-6)
点(1,1)
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-2
-1
0
1
2
y=-6x
12
6
0
-6
-12
y=-6x+5
17
11
5
-1
-7
O
x
y
y=-6x
①画函数y=-6x的图象
6
3
-3
-6
-3
-6
3
6
②用同样的方法画函数y=-6x+5的图象
描点;
连线.
y=-6x+5
选择两个点.
点(0,5)
思
考
比较右边两个函数图象,你能发现什么?
O
x
y
y=-6x
6
3
-3
-6
-3
-6
3
6
y=-6x+5
(1)这两个函数的图象形状都是 ,并且倾斜程度 .
(2)函数y=-6x的图象经过 ,函数y=-6x+5的图象与y轴交于 ,即它可以看作由直线y=-6x向 平移 个单位长度而得到.
一条直线
相同
原点
(0,5)
O
x
y
y=-6x
6
3
-3
-6
-3
-6
3
6
y=-6x+5
右
5
联系上面的发现,你能归纳出一次函数y=kx+b(k≠0)与正比例函数y=kx(k≠0)之间的关系吗?
直线y=kx+b可以看作由直线y=kx平移|b|个单位长度得到.当b>0时,向上平移;当b<0时,向下平移 .
一次函数图象的画法
2.平移法:直线y=kx+b可以看作由直线y=kx平移|b|个单位长度得到.当b>0时,向上平移;当b<0,向下平移 .
1.两点法:由于两点确定一条直线,所以在平面直角坐标系中画出一次函数的图象时,先描出适合解析式的两点,再通过这两点作直线即可.
归纳小结
探
究
画出函数y=x+1,y=-x+1及y=2x+1 y=-2x+l的图象 .并思考一次函数解析式y=kx+b(k, b是常数,k≠0)中,k、b的正负对函数图象有什么影响?
一次函数的性质
分别画出下面四个函数的图象.
y=x+1
y=-x+1
y=2x+1
y=-2x+l
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}y=kx+b
图象经过的象限
y和x的变化
k>0
b>0
b=0
b<0
k<0
b>0
b=0
b<0
观察图象,填写表格.
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
y随x的增大
而增大
y随x的增大
而减小
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}y=kx+b
图象经过的象限
y和x的变化
k>0
b>0
b=0
b<0
k<0
b>0
b=0
b<0
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
y随x的增大
而增大
y随x的增大
而减小
你能从表格中归纳出一次函数的性质吗?
你能从表格中归纳出一次函数的性质吗?
当k>0时,直线从左向右上升,即y随x的增大而增大.
当k<0时,直线从左向右下降,即y随x的增大而减小.
A
1.一次函数y=x+2的图象大致是( )
A
B
C
D
课堂练习
2.在同一直角坐标系中,对于函数:①y=-x-1,②y=x+1,③y=-x+1,④y=-2x-1的图象,下列说法不正确的是( )
A.通过点(-1,0)的是①和③
B.两直线的交点在y轴负半轴上的是①和④
C.相互平行的是①和③
D.关于y轴对称的是②和③
A
课堂练习
3.已知正比例函数y=(k-3)x,若y随x的增大而增大,则k的取值范围是( )
A.k<0 B.k>0
C.k<3 D.k>3
D
4.若一次函数y=(2m-1)x+3-2m的图象经过第一、二、四象限,则m的取值范围是m< .
课堂练习
5.下列关于一次函数y=-2x+1的说法:
①y随x的增大而减小;
②图象与直线y=-2x平行;
③图象与y轴的交点坐标是(0,1);
④图象经过第一、二、四象限.
其中正确的有 个.
4
课堂练习
6.在平面直角坐标系中画出函数y=-12x+3的图象.
(1)在图象上标出横坐标为-4的点A,并写出它的坐标;
(2)在图象上标出与y轴的距离是2个单位长度的点,并写出它的坐标.
课堂练习
7.一次函数y=(2a+4)x-(3-b),当a,b为何值时:
a>-2,b为任意实数
(2)图象经过第二、三、四象限;
(1)y随x的增大而增大;
a<-2,b<3
课堂练习
7.一次函数y=(2a+4)x-(3-b),当a,b为何值时:
a≠-2,b>3
(4)图象过原点.
(3)图象与y轴的交点在x轴上方;
a≠-2,b=3
课堂练习
1.一次函数图象的画法
平移法
两点法
当k>0时,直线从左向右上升,即y随x的增大而增大.
当k<0时,直线从左向右下降,即y随x的增大而减小.
2.一次函数的性质
课堂小结
https://www.21cnjy.com/help/help_extract.php
