19.2 一次函数的图象与性质 课件 (59张)
文档属性
| 名称 | 19.2 一次函数的图象与性质 课件 (59张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 20:36:21 | ||
图片预览







文档简介
(共59张PPT)
第十九章
19.2.4
一次函数的图象与性质
人教版数学八年级下册
1.一次函数的图象.
2.系数相等的一次函数图象的位置关系.
3.一次函数y=kx+b(k≠0)的性质.
学习目标
正比例函数是特殊的一次函数,正比例函数的图象是一条直线,那么一次函数的图象也是一条直线吗?从表达式上看,正比例函数与一次函数相差什么?如果体现在图象上又会有怎样的关系呢?
通过本节课的学习,同学们就会明白了,下面就让我们一起来学习本节课的内容.
导入新知
1
知识点
一次函数的图象
例1
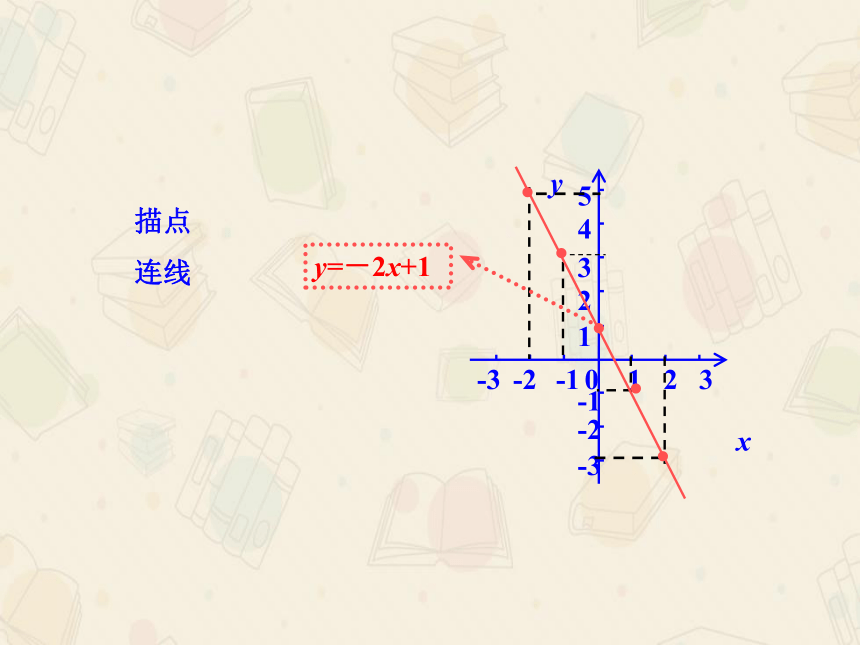
画出一次函数y=-2x+1的图象.
解:列表:
x
…
-2
-1
0
1
2
…
y
…
5
3
1
-1
-3
…
合作探究
描点
连线
y
x
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
y=-2x+1
一次函数y=kx+b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了.
一次函数y=kx+b的图象也称为直线y=kx+b.
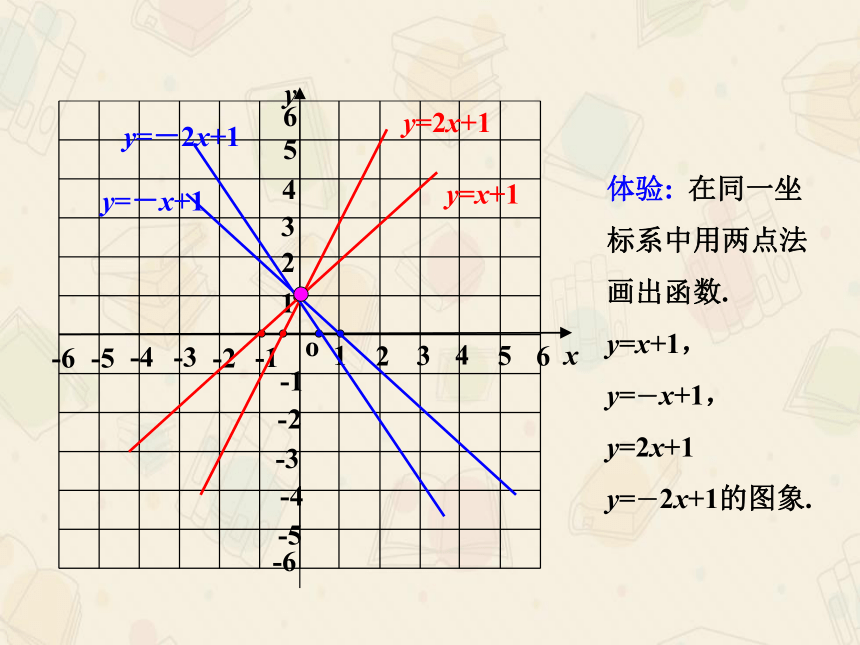
体验:
在同一坐标系中用两点法画出函数.
y=x+1,
y=-x+1,
y=2x+1
y=-2x+1的图象.
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y=x+1
y=-x+1
y=2x+1
y=-2x+1
两点法:由于两点确定一条直线,因此在平面直角
坐标系中画一次函数的图象时,先描出适合关系式
的两点,再过这两点作直线即可.通常选取(0,b)
和
,即与坐标轴相交的两点.
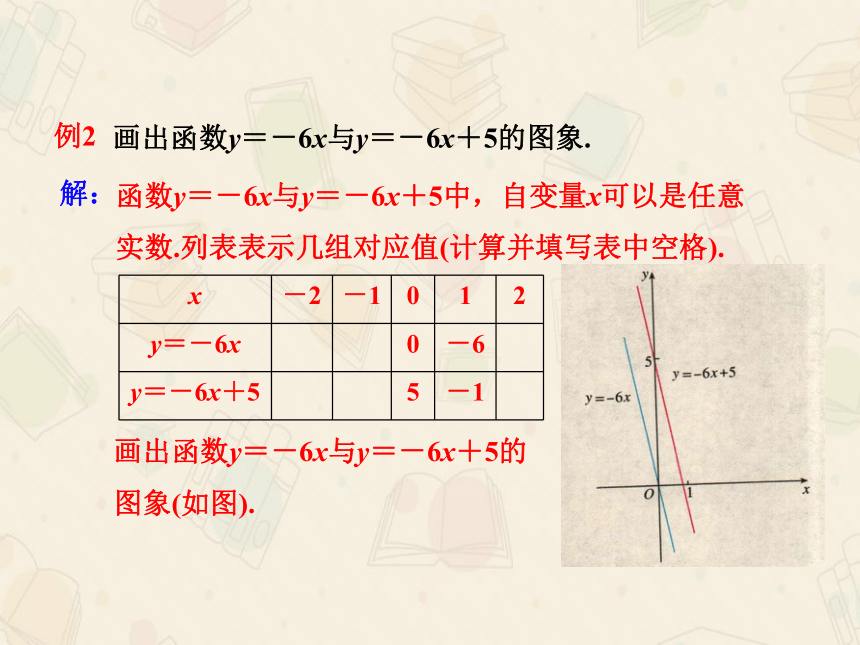
例2
画出函数y=-6x与y=-6x+5的图象.
函数y=-6x与y=-6x+5中,自变量x可以是任意
实数.列表表示几组对应值(计算并填写表中空格).
解:
x
-2
-1
0
1
2
y=-6x
0
-6
y=-6x+5
5
-1
画出函数y=-6x与y=-6x+5的
图象(如图).
画一次函数y=kx+b(k≠0)的图象,通常选取该
直线与y轴的交点(横坐标为0的点)和直线与x轴的交
点(纵坐标为0的点),由两点确定一条直线得一次函
数的图象.
新知小结
1
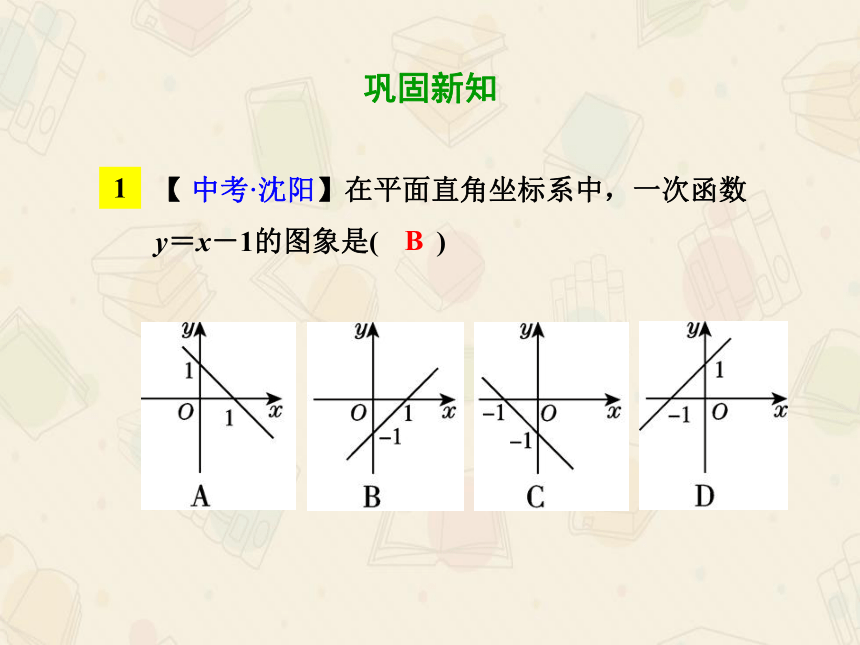
【
中考·沈阳】在平面直角坐标系中,一次函数
y=x-1的图象是( )
B
巩固新知
2
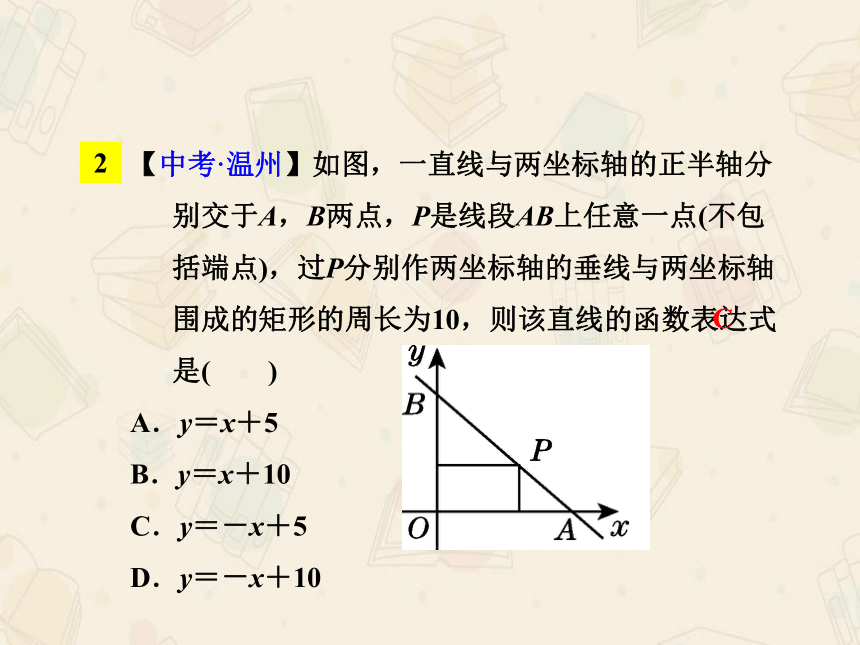
【中考·温州】如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )
A.y=x+5
B.y=x+10
C.y=-x+5
D.y=-x+10
C
3
【
中考·齐齐哈尔】已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确
反映y与x之间函数关系的图象是( )
D
4
【中考·酒泉】在平面直角坐标系中,一次函数y=kx+b的图象如图所示,观察图象可得( )
A.k>0,b>0
B.k>0,b<0
C.k<0,b>0
D.k<0,b<0
A
2
知识点
系数相等的一次函数图象的位置关系
比较一次函数y=kx+b(k≠0)与正比例函数y=
kx(k≠0)的解析式,容易得出:
一次函数y=kx+b(k≠0)的图象可以由直线
y=kx平移|b|个单位长度得到(当b>时,向上平移;
当b<0时,向下平移).一次函数y=kx+b(k≠0)的图
象也是一条直线,我们称它为直线y=kx+b.
合作探究
从
k、b的值看一次函数的图像
(1)当k>0,b>0时,图象过一、二、三象限;
(2)当k>0,b<0时,图象过一、三、四象限;
(3)当k<0,b>0时,图象过一、二、四象限;
(4)当k<0,b<0时,图象过二、三、四象限.
例3
已知直线y=(1-3k)x+2k-1.
(1)k为何值时,直线与y轴交点的纵坐标是-2?
(2)k为何值时,直线经过第二、三、四象限?
(3)k为何值时,已知直线与直线
y=-3x-5平行?
(1)可令2k-1=-2或将(0,-2)代入函数解析式即可求
得k值;
(2)直线经过第二、三、四象限,说明y=kx+b中的k<0,
b<0,即
解不等式组求出k的取值范围即可;
(3)两直线若平行,则它们的自变量的系数应相等,
所以1-3k=-3且2k-1≠-5,可求出k值.
导引:
(1)当x=0时,y=-2,即当2k-1=-2,k=
时,
直线与y轴交点的纵坐标是-2.
(2)当
直线经过第二、三、四
象限.
(3)当1-3k=-3,即当
时,2k-1=
≠-5,
此时,已知直线与直线
y=-3x-5平行.
解:
直线经过第二、三、四象限与不经过第一象限
的区别是:经过第二、三、四象限时函数解析式中b
不能等于0;不经过第一象限时函数解析式中的b可
能等于0.
新知小结
【中考·葫芦岛】一次函数y=(m-2)x+3的图
象如图所示,则m的取值范围是( )
A.m<2
B.0<m<2
C.m<0
D.m>2
1
A
巩固新知
【中考·巴彦淖尔】如图,直线l经过第一、二、四象限,l的解析式是y=(m-3)x+m+2,则m的取值范围在数轴上表示为( )
2
C
【中考·赤峰】将一次函数y=2x-3的图象沿y轴向上平移8个单位长度,所得直线对应的函数解析式为( )
A.y=2x-5
B.y=2x+5
C.y=2x+8
D.y=2x-8
3
B
3
知识点
一次函数y=kx+b(k≠0)的性质
做一做
在同一直角坐标系内分别画出一次函数y=2x+3,y=-x,y=
-x+3和y=5x-2的图象.
议一议
上述四个函数中,随着x值的增大,y的值分别如何变化?相应图象上点的变化趋势如何?
合作探究
例4
画出函数y=2x-1与y=-0.5x+1的图象.
由于一次函数的图象是直线,因此只要确定两个点
就能画出它.
分析:
列表表示当x=0,x=1时两个函数的对应值(见下表).
解:
x
0
1
y=2x-1
-1
1
y=-0.5x+l
1
0.5
过点(0,
-1)与点(1,1)画出直线y=2x-1;过点
(0,
1)与点(1,0.5)
画出直线y=-0.5x+1.(如图)
先画直线y=2x
与y=-0.5x
,再分
别平移它们,也能
得到直线
y=2x-1
与y=-0.5x+1.
探究
画出函数y=x+l,y=-x+l,y=2x+1,
y=-2x
+1的图象.由它们联想:一次函数解析式
y=kx+b(k,b是常数,k≠0)中,k的正负对函数图
象有什么影响?
观察前面一次函数的图象,可以发现规律:
当k>0时,直线y=kx+b从左向右上升;
当k<0时,直线y=kx+b从左向右下降.
由此可
知,一次函数y=kx+b(k,b是常数,k≠0)
具有如下性质:
当k>0时,y随x的增大而増大;
当k<0时,y随x的增大而减小.
新知小结
直线y=2x-3与x轴交点坐标为___________,与y轴交点坐标为___________,象经过
_______________象限,y随x的增大而___________.
1
(
,0)
(0,-3)
第一、三、四
增大
巩固新知
在同一直角坐标系中画出下列函数的图象,并指出每小题中三个函数的图象有什么关系.
(1)
y=x-1,y=x,y=x+1;
(2)
y=-2x-1,
y=-2x,
y=-2x+1.
2
(1)函数y=x-1,y=x,y=x+1的图象如图①.
(2)函数y=-2x-1,y=-2x,y=-2x+1的图象
如图②.每小题中三个函数的图象均互相平行.
解:
分别在同一直角坐标系中画出下列(1)
(2)中各函数的图象,并指出每组函数图象的共同之处.
(1)
y=
x+1,y=x+1,y=2x+1,
(2)
y=-
x-1,y=-x-1,y=-2x-1,
3
(1)图象如图①所示,它们的共同之处是都经过点(0,1).
(2)图象如图②,它们的共同之处是都经过点(0,-1).
解:
下列函数中,同时满足下面两个条件的是( )
①y随着x的增大而增大;
②其图象与x轴的正半轴相交.
A.y=-2x-1
B.y=-2x+1
C.y=2x-1
D.y=2x+1
4
C
1
知识小结
告诉大家本节课你的收获!
3.会用:
一次函数的性质
1.会画:
用两点法画一次函数的图象
2.会求:
一次函数与坐标轴的交点
归纳新知
已知一次函数y=kx+b,当-3≤x≤1时,对应的y值为-1≤y≤8,则b的值是( )
A.
B.
C.
或
D.
2
易错小结
C
易错点:对函数性质理解不透而漏解.
①将x=1,y=8代入,得8=k+b,将x=-3,y=-1代入,
得-1=-3k+b,解得k=
,b=
,∴函数解析式为y=
x+
,经检验符合题意;②将x=1,y=-1,代入得-1
=k+b,将x=-3,y=8代入得8=-3k+b,解得k=-
,
b=
,函数解析式为y=-
x+
,经检验符合题意;综
上可得b=
或
.故选C.
b
b
左
右
一、三、四
课后练习
<0
下降
>0
二、三、四
8
D
C
k2
C
A
【答案】B
k<0
D
B
B
解:由题意得m-2=0,则m=2.
由题意得8-2m<0,则m>4.
再见
第十九章
19.2.4
一次函数的图象与性质
人教版数学八年级下册
1.一次函数的图象.
2.系数相等的一次函数图象的位置关系.
3.一次函数y=kx+b(k≠0)的性质.
学习目标
正比例函数是特殊的一次函数,正比例函数的图象是一条直线,那么一次函数的图象也是一条直线吗?从表达式上看,正比例函数与一次函数相差什么?如果体现在图象上又会有怎样的关系呢?
通过本节课的学习,同学们就会明白了,下面就让我们一起来学习本节课的内容.
导入新知
1
知识点
一次函数的图象
例1
画出一次函数y=-2x+1的图象.
解:列表:
x
…
-2
-1
0
1
2
…
y
…
5
3
1
-1
-3
…
合作探究
描点
连线
y
x
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
y=-2x+1
一次函数y=kx+b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了.
一次函数y=kx+b的图象也称为直线y=kx+b.
体验:
在同一坐标系中用两点法画出函数.
y=x+1,
y=-x+1,
y=2x+1
y=-2x+1的图象.
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y=x+1
y=-x+1
y=2x+1
y=-2x+1
两点法:由于两点确定一条直线,因此在平面直角
坐标系中画一次函数的图象时,先描出适合关系式
的两点,再过这两点作直线即可.通常选取(0,b)
和
,即与坐标轴相交的两点.
例2
画出函数y=-6x与y=-6x+5的图象.
函数y=-6x与y=-6x+5中,自变量x可以是任意
实数.列表表示几组对应值(计算并填写表中空格).
解:
x
-2
-1
0
1
2
y=-6x
0
-6
y=-6x+5
5
-1
画出函数y=-6x与y=-6x+5的
图象(如图).
画一次函数y=kx+b(k≠0)的图象,通常选取该
直线与y轴的交点(横坐标为0的点)和直线与x轴的交
点(纵坐标为0的点),由两点确定一条直线得一次函
数的图象.
新知小结
1
【
中考·沈阳】在平面直角坐标系中,一次函数
y=x-1的图象是( )
B
巩固新知
2
【中考·温州】如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )
A.y=x+5
B.y=x+10
C.y=-x+5
D.y=-x+10
C
3
【
中考·齐齐哈尔】已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确
反映y与x之间函数关系的图象是( )
D
4
【中考·酒泉】在平面直角坐标系中,一次函数y=kx+b的图象如图所示,观察图象可得( )
A.k>0,b>0
B.k>0,b<0
C.k<0,b>0
D.k<0,b<0
A
2
知识点
系数相等的一次函数图象的位置关系
比较一次函数y=kx+b(k≠0)与正比例函数y=
kx(k≠0)的解析式,容易得出:
一次函数y=kx+b(k≠0)的图象可以由直线
y=kx平移|b|个单位长度得到(当b>时,向上平移;
当b<0时,向下平移).一次函数y=kx+b(k≠0)的图
象也是一条直线,我们称它为直线y=kx+b.
合作探究
从
k、b的值看一次函数的图像
(1)当k>0,b>0时,图象过一、二、三象限;
(2)当k>0,b<0时,图象过一、三、四象限;
(3)当k<0,b>0时,图象过一、二、四象限;
(4)当k<0,b<0时,图象过二、三、四象限.
例3
已知直线y=(1-3k)x+2k-1.
(1)k为何值时,直线与y轴交点的纵坐标是-2?
(2)k为何值时,直线经过第二、三、四象限?
(3)k为何值时,已知直线与直线
y=-3x-5平行?
(1)可令2k-1=-2或将(0,-2)代入函数解析式即可求
得k值;
(2)直线经过第二、三、四象限,说明y=kx+b中的k<0,
b<0,即
解不等式组求出k的取值范围即可;
(3)两直线若平行,则它们的自变量的系数应相等,
所以1-3k=-3且2k-1≠-5,可求出k值.
导引:
(1)当x=0时,y=-2,即当2k-1=-2,k=
时,
直线与y轴交点的纵坐标是-2.
(2)当
直线经过第二、三、四
象限.
(3)当1-3k=-3,即当
时,2k-1=
≠-5,
此时,已知直线与直线
y=-3x-5平行.
解:
直线经过第二、三、四象限与不经过第一象限
的区别是:经过第二、三、四象限时函数解析式中b
不能等于0;不经过第一象限时函数解析式中的b可
能等于0.
新知小结
【中考·葫芦岛】一次函数y=(m-2)x+3的图
象如图所示,则m的取值范围是( )
A.m<2
B.0<m<2
C.m<0
D.m>2
1
A
巩固新知
【中考·巴彦淖尔】如图,直线l经过第一、二、四象限,l的解析式是y=(m-3)x+m+2,则m的取值范围在数轴上表示为( )
2
C
【中考·赤峰】将一次函数y=2x-3的图象沿y轴向上平移8个单位长度,所得直线对应的函数解析式为( )
A.y=2x-5
B.y=2x+5
C.y=2x+8
D.y=2x-8
3
B
3
知识点
一次函数y=kx+b(k≠0)的性质
做一做
在同一直角坐标系内分别画出一次函数y=2x+3,y=-x,y=
-x+3和y=5x-2的图象.
议一议
上述四个函数中,随着x值的增大,y的值分别如何变化?相应图象上点的变化趋势如何?
合作探究
例4
画出函数y=2x-1与y=-0.5x+1的图象.
由于一次函数的图象是直线,因此只要确定两个点
就能画出它.
分析:
列表表示当x=0,x=1时两个函数的对应值(见下表).
解:
x
0
1
y=2x-1
-1
1
y=-0.5x+l
1
0.5
过点(0,
-1)与点(1,1)画出直线y=2x-1;过点
(0,
1)与点(1,0.5)
画出直线y=-0.5x+1.(如图)
先画直线y=2x
与y=-0.5x
,再分
别平移它们,也能
得到直线
y=2x-1
与y=-0.5x+1.
探究
画出函数y=x+l,y=-x+l,y=2x+1,
y=-2x
+1的图象.由它们联想:一次函数解析式
y=kx+b(k,b是常数,k≠0)中,k的正负对函数图
象有什么影响?
观察前面一次函数的图象,可以发现规律:
当k>0时,直线y=kx+b从左向右上升;
当k<0时,直线y=kx+b从左向右下降.
由此可
知,一次函数y=kx+b(k,b是常数,k≠0)
具有如下性质:
当k>0时,y随x的增大而増大;
当k<0时,y随x的增大而减小.
新知小结
直线y=2x-3与x轴交点坐标为___________,与y轴交点坐标为___________,象经过
_______________象限,y随x的增大而___________.
1
(
,0)
(0,-3)
第一、三、四
增大
巩固新知
在同一直角坐标系中画出下列函数的图象,并指出每小题中三个函数的图象有什么关系.
(1)
y=x-1,y=x,y=x+1;
(2)
y=-2x-1,
y=-2x,
y=-2x+1.
2
(1)函数y=x-1,y=x,y=x+1的图象如图①.
(2)函数y=-2x-1,y=-2x,y=-2x+1的图象
如图②.每小题中三个函数的图象均互相平行.
解:
分别在同一直角坐标系中画出下列(1)
(2)中各函数的图象,并指出每组函数图象的共同之处.
(1)
y=
x+1,y=x+1,y=2x+1,
(2)
y=-
x-1,y=-x-1,y=-2x-1,
3
(1)图象如图①所示,它们的共同之处是都经过点(0,1).
(2)图象如图②,它们的共同之处是都经过点(0,-1).
解:
下列函数中,同时满足下面两个条件的是( )
①y随着x的增大而增大;
②其图象与x轴的正半轴相交.
A.y=-2x-1
B.y=-2x+1
C.y=2x-1
D.y=2x+1
4
C
1
知识小结
告诉大家本节课你的收获!
3.会用:
一次函数的性质
1.会画:
用两点法画一次函数的图象
2.会求:
一次函数与坐标轴的交点
归纳新知
已知一次函数y=kx+b,当-3≤x≤1时,对应的y值为-1≤y≤8,则b的值是( )
A.
B.
C.
或
D.
2
易错小结
C
易错点:对函数性质理解不透而漏解.
①将x=1,y=8代入,得8=k+b,将x=-3,y=-1代入,
得-1=-3k+b,解得k=
,b=
,∴函数解析式为y=
x+
,经检验符合题意;②将x=1,y=-1,代入得-1
=k+b,将x=-3,y=8代入得8=-3k+b,解得k=-
,
b=
,函数解析式为y=-
x+
,经检验符合题意;综
上可得b=
或
.故选C.
b
b
左
右
一、三、四
课后练习
<0
下降
>0
二、三、四
8
D
C
k2
C
A
【答案】B
k<0
D
B
B
解:由题意得m-2=0,则m=2.
由题意得8-2m<0,则m>4.
再见
