六年级下册数学课件 圆柱圆锥复习课 苏教版(20张ppt)
文档属性
| 名称 | 六年级下册数学课件 圆柱圆锥复习课 苏教版(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 20:57:38 | ||
图片预览






文档简介
圆柱圆锥
六下第一单元
01
目录
CONTENT
圆柱圆锥的认识
圆柱表面积
综合运用
02
04
03
圆柱圆锥体积
第一部分
圆柱圆锥的认识
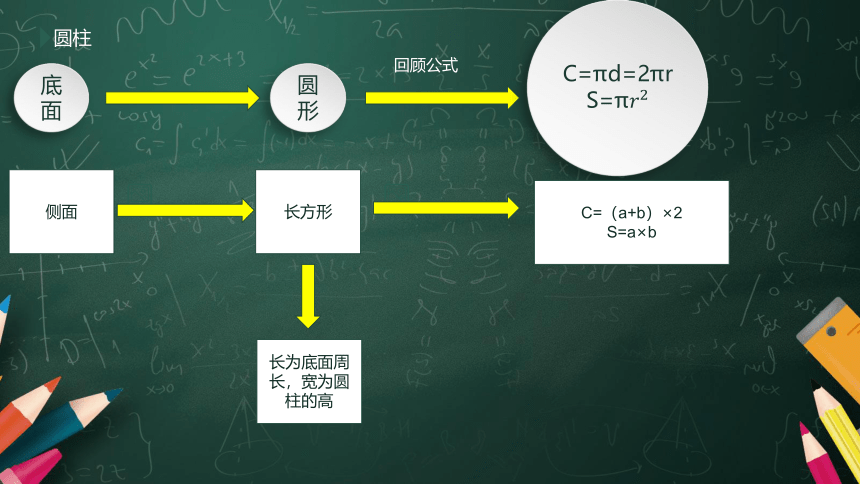
①圆柱由一个上底面、一个下底面和一个侧面组成。上下底面是两个完全相同的圆形;侧面是一个曲面(展开是长方形)。
②圆柱的高:上下底面之间的距离。圆柱有无数条高,每条高相等。
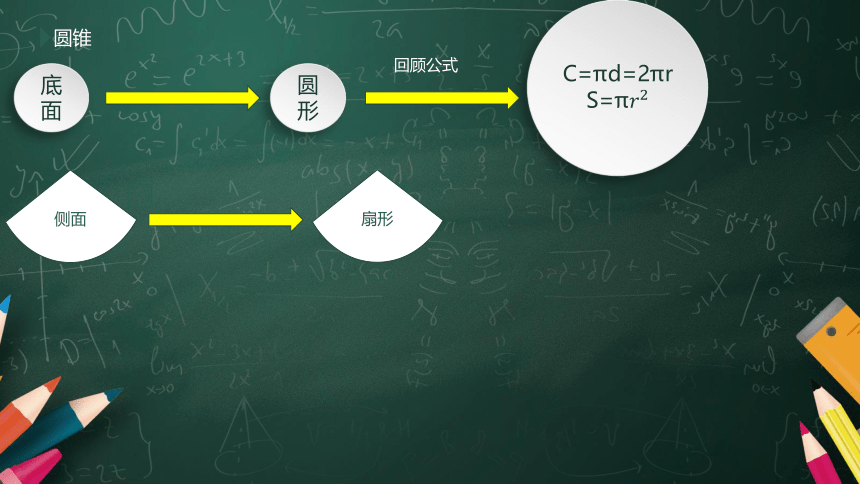
①圆锥由一个底面和一个侧面组成。底面是一个圆形;侧面是一个曲面(展开是扇形)。
②圆锥的高:圆锥的顶点到底面圆心的距离。圆锥只有一条高。
圆柱圆锥的基本概念
圆柱
底面
圆形
C=πd=2πr
S=π????2
?
回顾公式
侧面
长方形
C=(a+b)×2
S=a×b
长为底面周长,宽为圆柱的高
圆锥
底面
圆形
C=πd=2πr
S=π????2
?
回顾公式
侧面
扇形
例1:
1.一个圆柱的侧面展开图是正方形,这个圆柱的高是6.28厘米,则圆柱的底面半径是( )厘米。圆柱底面面积是( )平方厘米。
侧面是正方形:底面周长=高=6.28厘米
πd=6.28 d=2厘米 r=1厘米 S=3.14平方厘米
1
3.14
2.一个直角三角形的两条直角边分别是5厘米、4厘米,如果以这个三角形5厘米的直角边为轴旋转后会得到的一个( )体,这个形体的底面半径是( )厘米,这个形体的高是( )厘米。如果以这个三角形4厘米的直角边为轴旋转后会得到的一个( )体,这个形体的底面半径是( )厘米,这个形体的高是( )厘米。
圆锥
4
5
圆锥
5
4
第二部分
圆柱的表面积
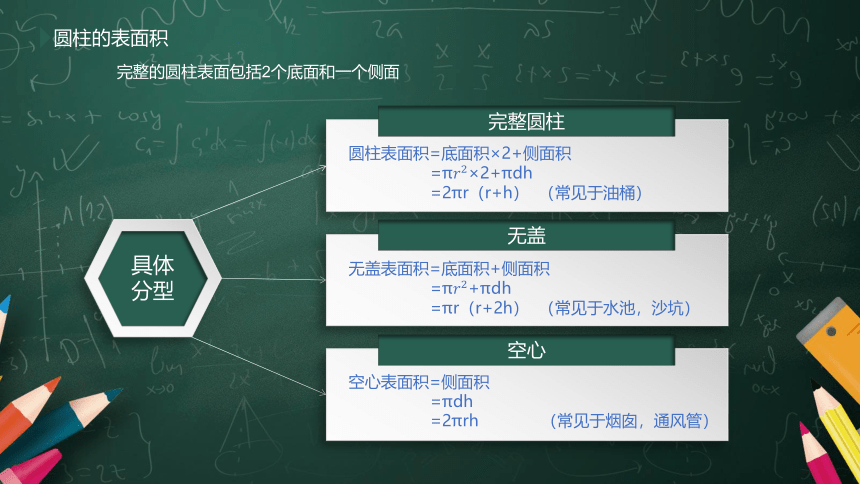
圆柱的表面积
完整圆柱
圆柱表面积=底面积×2+侧面积
=π????2×2+πdh
=2πr(r+h) (常见于油桶)
?
具体分型
无盖
空心
空心表面积=侧面积
=πdh
=2πrh (常见于烟囱,通风管)
完整的圆柱表面包括2个底面和一个侧面
无盖表面积=底面积+侧面积
=π????2+πdh
=πr(r+2h) (常见于水池,沙坑)
?
例2:
1.用铁皮制作一个圆柱形烟囱,要求底面半径是3分米,高是15分米,制作100这个烟囱至少需要铁皮多少平方米?(接头处不计)
本题关键点:1.烟囱是空心的(隐藏条件)
2.单位转换(易错)
空心表面积=侧面积=2πrh=2×3.14×3×15=282.6平方分米
100个=282.6×100=28260平方分米=282.6平方米
例2:
2.一个圆柱形蓄水池,底面周长是25.12米,高是4米,将这个蓄水池四周及底部抹上水泥。如果每平方米要用水泥20千克,一共要用多少千克水泥?
本题关键点:蓄水池只要侧面和一个底面(相当于无盖)
半径r=25.12÷3.14÷2=4cm
无盖表面积=侧面积+一个底面=Ch+ π????2?=25.12×4+3.14×4×4=150.72平方米
总质量=150.72×20=3014.4千克
?
例2:
3.把一个棱长6分米的正方体木块,削成一个最大的一圆柱体,这个圆柱的表面积是多少立方分米?
本题关键点:削成的圆柱底面直径和高就是正方体的棱长
底面半径=6÷2=3分米
表面积=底面积×2+侧面积
= π????2×2+πdh
=3.14×3×3×2+3.14×6×6
=169.56 平方厘米
?
第三部分
圆柱圆锥的体积
圆柱体积推导方法(类似于圆)
高
长方体的体积=底面积 × 高
圆柱体的体积=
×
底面积
圆锥体积推导方法
1
2
3
4
圆柱与圆锥等底等高
将一个圆锥中的液体倒入圆柱
再将一个圆锥中的液体倒入圆柱
将最后一个圆锥中的液体倒入圆柱
圆柱体积等于3个等底等高的圆锥体积
圆柱圆锥的体积公式
圆柱体积公式
相关公式
①已知半径和高,V圆柱=πr2h
②已知直径和高,V圆柱=π(d÷2)2h
③已知周长和高,V圆柱=π(C÷2π)2h
圆锥体积公式
相关公式
①已知半径和高,V圆锥=1/3πr2h
②已知直径和高,V圆锥=1/3π(d÷2)2h
③已知周长和高,V圆锥=1/3π(C÷2π)2h
例3:
1.一个长方体容器,长5厘米,宽4厘米,高3厘米,装满水后将水全部倒入一个高6厘米的圆锥形的容器内刚好装满。这个圆锥形容器的底面积是多少平方厘米?
本题关键:本题属于等积变换。长方体体积=圆锥体积
要注意的是由体积求底面积是要先乘3(类似三角形由面积求底或高要先乘2)
底面积=体积×3÷高=5×4×3×3÷6=30平方厘米
例3:
2.如图,想想办法,你能否求出它的体积?( 单位:分米)
本题关键:本题图形属于不规则图形。处理不规则图形的原则就是利用割补法变成规则图形。本题中我们可以利用2个一样的不规则图形拼成一个圆柱。
体积=圆柱体积÷2=π×(2÷1)2×(4+3)÷2=10.99 立方分米
?
2
4
3
例3:
3.将一块长方形铁皮,利用图中阴影的部分,刚好制成一个油桶,求这个油桶的体积。
本题关键:本题需要通过逻辑推理得出底面周长=长方形的长
设直径为x,那么宽为2x。
油桶为圆柱形,底面周长为πd=3.14x >宽 ,所以长方形的长是底面周长
解:设底面直径为x
3.14x+x=16.56 x=4 所以r=2cm
V=π????2h=3.14×4×8=100.48????????3
?
例3:
4.如图,将三角形以斜边为轴旋转一周,计算所得立体图形的体积。(单位:厘米)
5
3
4
本题关键:由斜边旋转得来的为不规则图形,由2个底面积相等但高不相等的圆锥组成。目前已知2个圆锥高的和为5cm。关键在于求出底面积。要求底面积必须知道底面半径。
由直角三角形的特性可以求出底面半径=3×4÷5=2.4cm
体积=3.14×2.4×2.4×5=90.432 平方厘米
第四部分
综合运用
在此处添加详细描述文本,尽量与标题文本语言风格相符,语言描述尽量简洁生动,尽可能概括出段落内容。
例4: 切割问题:横切,竖切
1.把一个圆柱形的木块沿底面半径竖直切成两部分,表面积比原来增加了600cm2,已知圆柱形木料的底面直径为10cm,这根木料的体积是( )cm3
本题关键:本题属于竖切。竖切多出来的面是长方形,长为高,宽为底面直径。
高=600÷2÷10=30cm 体积=5×5×3.14×30=2355立方厘米
2.把一个底面半径是2分米,长是9分米的圆柱形木头锯成长短不同的三小段圆柱形木头,表面积增加了多少平方分米?
本题关键:本题属于横切。横切多出来的面是底面。切成3个=切2次=多4个面。
表面积增加=3.14×2×2×4=50.24 平方分米
例5:等积转换
1.求这只瓶子的容积。
本题关键:本题属于等积变换。瓶口不规则图形体积=高为4cm的圆柱体积
所以瓶子容积可以转化为一个高是(16+4)cm的圆柱的体积
体积=(8÷2)×(8÷2)×3.14×(16+4)
=1004.8立方厘米
=1004.8 ml
d:8cm
专题
圆柱圆锥的体积转换(考点)
例6:公式正向推导:由高和底面得出体积
1.如下图,圆柱形烧杯与圆锥形杯子的底面积相等,将圆柱形烧杯装满水后倒入圆锥形杯子,能装( )杯。
9
2.如下图把一个棱长6cm的正方体木块加工成一个最大的圆锥,这个圆锥的体积是
( )cm3。
56.52
例7:公式逆向推导:由体积得出高或底面的关系
1.一个圆柱底面面积是圆锥的2倍,要使它们都体积相等,圆柱的高应该是圆锥高的( )。
????柱=????锥
?
????柱·h柱=13????锥h锥
?
2×????锥·h柱=13????锥h锥
?
????柱= 2×????锥
?
2h柱=13h锥
?
h柱=16h锥
?
16
?
例7:公式逆向推导:由体积得出高或底面的关系
2.一个圆柱和一个圆锥体积相等,已知圆锥体和圆柱的高的比是9:1,圆柱体底面积和圆锥体底面积的比是多少?
????柱=????锥
?
????柱·h柱=13????锥h锥
?
????柱·h柱=13????锥h柱×9
?
h锥= 9×h柱
?
????柱=13????锥×9
?
????柱=3????锥
?
圆柱底面积:圆锥底面积=3:1
教学反思
圆柱圆锥的认识
圆柱圆锥的公式
牢记圆柱表面积,圆柱圆锥体积公式
公式的运用
能根据提议灵活运用公式解决问题,特别是一些非常规图形,能运用割补法进行转化
重难点
圆柱圆锥的体积转换是本章的重难点,初步与初中的代数理论衔接。题型较灵活,涉及比,分数,百分数。需要较强逻辑思维能力
掌握圆柱圆锥的基本特征以及圆柱圆锥的区别
感谢您的观看
六下第二单元圆柱圆锥
六下第一单元
01
目录
CONTENT
圆柱圆锥的认识
圆柱表面积
综合运用
02
04
03
圆柱圆锥体积
第一部分
圆柱圆锥的认识
①圆柱由一个上底面、一个下底面和一个侧面组成。上下底面是两个完全相同的圆形;侧面是一个曲面(展开是长方形)。
②圆柱的高:上下底面之间的距离。圆柱有无数条高,每条高相等。
①圆锥由一个底面和一个侧面组成。底面是一个圆形;侧面是一个曲面(展开是扇形)。
②圆锥的高:圆锥的顶点到底面圆心的距离。圆锥只有一条高。
圆柱圆锥的基本概念
圆柱
底面
圆形
C=πd=2πr
S=π????2
?
回顾公式
侧面
长方形
C=(a+b)×2
S=a×b
长为底面周长,宽为圆柱的高
圆锥
底面
圆形
C=πd=2πr
S=π????2
?
回顾公式
侧面
扇形
例1:
1.一个圆柱的侧面展开图是正方形,这个圆柱的高是6.28厘米,则圆柱的底面半径是( )厘米。圆柱底面面积是( )平方厘米。
侧面是正方形:底面周长=高=6.28厘米
πd=6.28 d=2厘米 r=1厘米 S=3.14平方厘米
1
3.14
2.一个直角三角形的两条直角边分别是5厘米、4厘米,如果以这个三角形5厘米的直角边为轴旋转后会得到的一个( )体,这个形体的底面半径是( )厘米,这个形体的高是( )厘米。如果以这个三角形4厘米的直角边为轴旋转后会得到的一个( )体,这个形体的底面半径是( )厘米,这个形体的高是( )厘米。
圆锥
4
5
圆锥
5
4
第二部分
圆柱的表面积
圆柱的表面积
完整圆柱
圆柱表面积=底面积×2+侧面积
=π????2×2+πdh
=2πr(r+h) (常见于油桶)
?
具体分型
无盖
空心
空心表面积=侧面积
=πdh
=2πrh (常见于烟囱,通风管)
完整的圆柱表面包括2个底面和一个侧面
无盖表面积=底面积+侧面积
=π????2+πdh
=πr(r+2h) (常见于水池,沙坑)
?
例2:
1.用铁皮制作一个圆柱形烟囱,要求底面半径是3分米,高是15分米,制作100这个烟囱至少需要铁皮多少平方米?(接头处不计)
本题关键点:1.烟囱是空心的(隐藏条件)
2.单位转换(易错)
空心表面积=侧面积=2πrh=2×3.14×3×15=282.6平方分米
100个=282.6×100=28260平方分米=282.6平方米
例2:
2.一个圆柱形蓄水池,底面周长是25.12米,高是4米,将这个蓄水池四周及底部抹上水泥。如果每平方米要用水泥20千克,一共要用多少千克水泥?
本题关键点:蓄水池只要侧面和一个底面(相当于无盖)
半径r=25.12÷3.14÷2=4cm
无盖表面积=侧面积+一个底面=Ch+ π????2?=25.12×4+3.14×4×4=150.72平方米
总质量=150.72×20=3014.4千克
?
例2:
3.把一个棱长6分米的正方体木块,削成一个最大的一圆柱体,这个圆柱的表面积是多少立方分米?
本题关键点:削成的圆柱底面直径和高就是正方体的棱长
底面半径=6÷2=3分米
表面积=底面积×2+侧面积
= π????2×2+πdh
=3.14×3×3×2+3.14×6×6
=169.56 平方厘米
?
第三部分
圆柱圆锥的体积
圆柱体积推导方法(类似于圆)
高
长方体的体积=底面积 × 高
圆柱体的体积=
×
底面积
圆锥体积推导方法
1
2
3
4
圆柱与圆锥等底等高
将一个圆锥中的液体倒入圆柱
再将一个圆锥中的液体倒入圆柱
将最后一个圆锥中的液体倒入圆柱
圆柱体积等于3个等底等高的圆锥体积
圆柱圆锥的体积公式
圆柱体积公式
相关公式
①已知半径和高,V圆柱=πr2h
②已知直径和高,V圆柱=π(d÷2)2h
③已知周长和高,V圆柱=π(C÷2π)2h
圆锥体积公式
相关公式
①已知半径和高,V圆锥=1/3πr2h
②已知直径和高,V圆锥=1/3π(d÷2)2h
③已知周长和高,V圆锥=1/3π(C÷2π)2h
例3:
1.一个长方体容器,长5厘米,宽4厘米,高3厘米,装满水后将水全部倒入一个高6厘米的圆锥形的容器内刚好装满。这个圆锥形容器的底面积是多少平方厘米?
本题关键:本题属于等积变换。长方体体积=圆锥体积
要注意的是由体积求底面积是要先乘3(类似三角形由面积求底或高要先乘2)
底面积=体积×3÷高=5×4×3×3÷6=30平方厘米
例3:
2.如图,想想办法,你能否求出它的体积?( 单位:分米)
本题关键:本题图形属于不规则图形。处理不规则图形的原则就是利用割补法变成规则图形。本题中我们可以利用2个一样的不规则图形拼成一个圆柱。
体积=圆柱体积÷2=π×(2÷1)2×(4+3)÷2=10.99 立方分米
?
2
4
3
例3:
3.将一块长方形铁皮,利用图中阴影的部分,刚好制成一个油桶,求这个油桶的体积。
本题关键:本题需要通过逻辑推理得出底面周长=长方形的长
设直径为x,那么宽为2x。
油桶为圆柱形,底面周长为πd=3.14x >宽 ,所以长方形的长是底面周长
解:设底面直径为x
3.14x+x=16.56 x=4 所以r=2cm
V=π????2h=3.14×4×8=100.48????????3
?
例3:
4.如图,将三角形以斜边为轴旋转一周,计算所得立体图形的体积。(单位:厘米)
5
3
4
本题关键:由斜边旋转得来的为不规则图形,由2个底面积相等但高不相等的圆锥组成。目前已知2个圆锥高的和为5cm。关键在于求出底面积。要求底面积必须知道底面半径。
由直角三角形的特性可以求出底面半径=3×4÷5=2.4cm
体积=3.14×2.4×2.4×5=90.432 平方厘米
第四部分
综合运用
在此处添加详细描述文本,尽量与标题文本语言风格相符,语言描述尽量简洁生动,尽可能概括出段落内容。
例4: 切割问题:横切,竖切
1.把一个圆柱形的木块沿底面半径竖直切成两部分,表面积比原来增加了600cm2,已知圆柱形木料的底面直径为10cm,这根木料的体积是( )cm3
本题关键:本题属于竖切。竖切多出来的面是长方形,长为高,宽为底面直径。
高=600÷2÷10=30cm 体积=5×5×3.14×30=2355立方厘米
2.把一个底面半径是2分米,长是9分米的圆柱形木头锯成长短不同的三小段圆柱形木头,表面积增加了多少平方分米?
本题关键:本题属于横切。横切多出来的面是底面。切成3个=切2次=多4个面。
表面积增加=3.14×2×2×4=50.24 平方分米
例5:等积转换
1.求这只瓶子的容积。
本题关键:本题属于等积变换。瓶口不规则图形体积=高为4cm的圆柱体积
所以瓶子容积可以转化为一个高是(16+4)cm的圆柱的体积
体积=(8÷2)×(8÷2)×3.14×(16+4)
=1004.8立方厘米
=1004.8 ml
d:8cm
专题
圆柱圆锥的体积转换(考点)
例6:公式正向推导:由高和底面得出体积
1.如下图,圆柱形烧杯与圆锥形杯子的底面积相等,将圆柱形烧杯装满水后倒入圆锥形杯子,能装( )杯。
9
2.如下图把一个棱长6cm的正方体木块加工成一个最大的圆锥,这个圆锥的体积是
( )cm3。
56.52
例7:公式逆向推导:由体积得出高或底面的关系
1.一个圆柱底面面积是圆锥的2倍,要使它们都体积相等,圆柱的高应该是圆锥高的( )。
????柱=????锥
?
????柱·h柱=13????锥h锥
?
2×????锥·h柱=13????锥h锥
?
????柱= 2×????锥
?
2h柱=13h锥
?
h柱=16h锥
?
16
?
例7:公式逆向推导:由体积得出高或底面的关系
2.一个圆柱和一个圆锥体积相等,已知圆锥体和圆柱的高的比是9:1,圆柱体底面积和圆锥体底面积的比是多少?
????柱=????锥
?
????柱·h柱=13????锥h锥
?
????柱·h柱=13????锥h柱×9
?
h锥= 9×h柱
?
????柱=13????锥×9
?
????柱=3????锥
?
圆柱底面积:圆锥底面积=3:1
教学反思
圆柱圆锥的认识
圆柱圆锥的公式
牢记圆柱表面积,圆柱圆锥体积公式
公式的运用
能根据提议灵活运用公式解决问题,特别是一些非常规图形,能运用割补法进行转化
重难点
圆柱圆锥的体积转换是本章的重难点,初步与初中的代数理论衔接。题型较灵活,涉及比,分数,百分数。需要较强逻辑思维能力
掌握圆柱圆锥的基本特征以及圆柱圆锥的区别
感谢您的观看
六下第二单元圆柱圆锥
