1.2.1排列第1课时排列与排列数公式 学案2020-2021学年高二数学下学期人教A版选修2-3 第一章计数原理
文档属性
| 名称 | 1.2.1排列第1课时排列与排列数公式 学案2020-2021学年高二数学下学期人教A版选修2-3 第一章计数原理 |  | |
| 格式 | doc | ||
| 文件大小 | 444.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 22:40:45 | ||
图片预览



文档简介
1.2 排列与组合
1.2.1 排列
第1课时 排列与排列数公式
[目标] 1.理解排列和排列数的特征.2.正确运用排列数公式进行计算.
[重点] 理解排列的概念,会用排列数公式进行计算.
[难点] 对排列的有序性的正确理解,排列数公式的逆用.
知识点一 排列的概念
[填一填]
1.排列的定义
一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
2.相同排列
两个排列相同,当且仅当两个排列的元素完全相同,且元素的排列顺序也相同.
[答一答]
1.排列的定义中包括哪两个基本内容?
提示:排列定义包括两个基本内容:一是“取出的元素不能重复”;二是“按照一定的顺序排列”.
2.两个排列若为相同的排列需具备哪些条件?
提示:需要具备两个条件:一是元素完全相同,二是元素的排列顺序完全相同.
3.判断一个具体问题是否为排列问题的关键是什么?
提示:判断一个具体问题是不是排列问题,关键看在安排取出的元素时是有序还是无序,有序就是排列,无序就不是排列.
知识点二 排列数公式
[填一填]
[答一答]
4.“排列数”与“一个排列”是否为同一个概念?
提示:不是同一概念.“一个排列”是指“从n个不同元素中取出m个元素,按照一定的顺序排成一列”,它不是一个数;“排列数”是指“从n个不同元素中取出m个元素的所有排列的个数”.例如,从a,b,c中任取2个元素的排列有ab,ba,ac,ca,bc,cb,共6个,6就是从a,b,c中任取2个元素的排列数.
5.对于排列数A中,m,n有什么要求?
提示:m、n∈N+,且m≤n.
6.在A=n(n-1)…(n-m+1)中右边共多少项的乘积.
提示:从n,(n-1),…,(n-m+1)以上m个数相乘,可得共m项.
7.为什么规定0!=1?
提示:为了使公式A=在m=n时也能成立,规定0!=1,这种规定说明:若一个元素都不取,则构成排列的情形只有1种.
1.对排列定义的四点说明
(1)定义的两个要素:
一是“从n个不同元素中取出m(m≤n)个元素”,要求取出的元素不能重复;二是“按照一定的顺序排列”.
(2)定义中“一定顺序”就是说与位置有关,选取的元素相同但顺序不同是不同的排列,在实际问题中,要由具体问题的性质和条件决定.
(3)对于两个排列,只有各元素完全相同,并且元素的排列顺序也完全相同时,才是相同排列.
(4)在定义中规定m≤n,如果m2.准确理解排列数公式
(1)公式中的n,m应该满足n,m∈N*,m≤n,当m>n时不成立.
(2)排列数有两个公式,第一个公式右边是若干数的连乘积,其特点是:第一个因数是n(下标),后面的每一个因数都比它前面的因数少1,最后一个因数为n-m+1(下标-上标+1),共有m(上标)个连续自然数相乘.
(3)排列数的第二个公式是阶乘的形式,所以又叫排列数的阶乘式,它是一个分式的形式,分子是下标n的阶乘,分母是下标减上标的阶乘,即(n-m)的阶乘,
(4)特别地,规定0!=1.这只是一种规定,不能按阶乘的含义作解释.
类型一 排列的概念
【例1】 判断下列问题是否是排列问题:
(1)某班共有50名同学,现要投票选举正、副班长各一人,共有多少种可能的选举结果?
(2)从2,3,5,7,9中任取两数分别作对数的底数和真数,有多少不同对数值?
(3)从1到10十个自然数中任取两个数组成点的坐标,可得多少个不同的点的坐标?
(4)从集合M={1,2,…,9}中,任取相异的两个元素作为a,b,可以得到多少个焦点在x轴上的椭圆方程+=1?
【分析】 由题目可获取以下主要信息:
对于(1),两人当班长,有正副之分;
对于(2),对数的底数与真数交换,其值也不同;
对于(3),点的坐标有横坐标与纵坐标之分;
对于(4),焦点在x轴上的椭圆方程,必须a>b.
解答本题,其关键是看问题的结果与选出的元素排列时跟顺序是否有关,有关即是排列问题,否则不是.
【解】 (1)是.选出的2人分别担任正、副班长,与顺序有关,所以该问题是排列问题;
(2)是.显然对数值与底数和真数的取值的不同有关系,与顺序有关.
(3)是.道理同上.
(4)不是.焦点在x轴上的椭圆,方程中的a、b必有a>b,a、b的大小一定.
排列的特点是“先取后排”,即先从n个不同的元素中取出m个元素,再按一定顺序把这m个元素排成一列.因此,判断一个问题是否为排列问题,只需考察与顺序是否有关,有关则是排列问题,无关则不是排列问题.
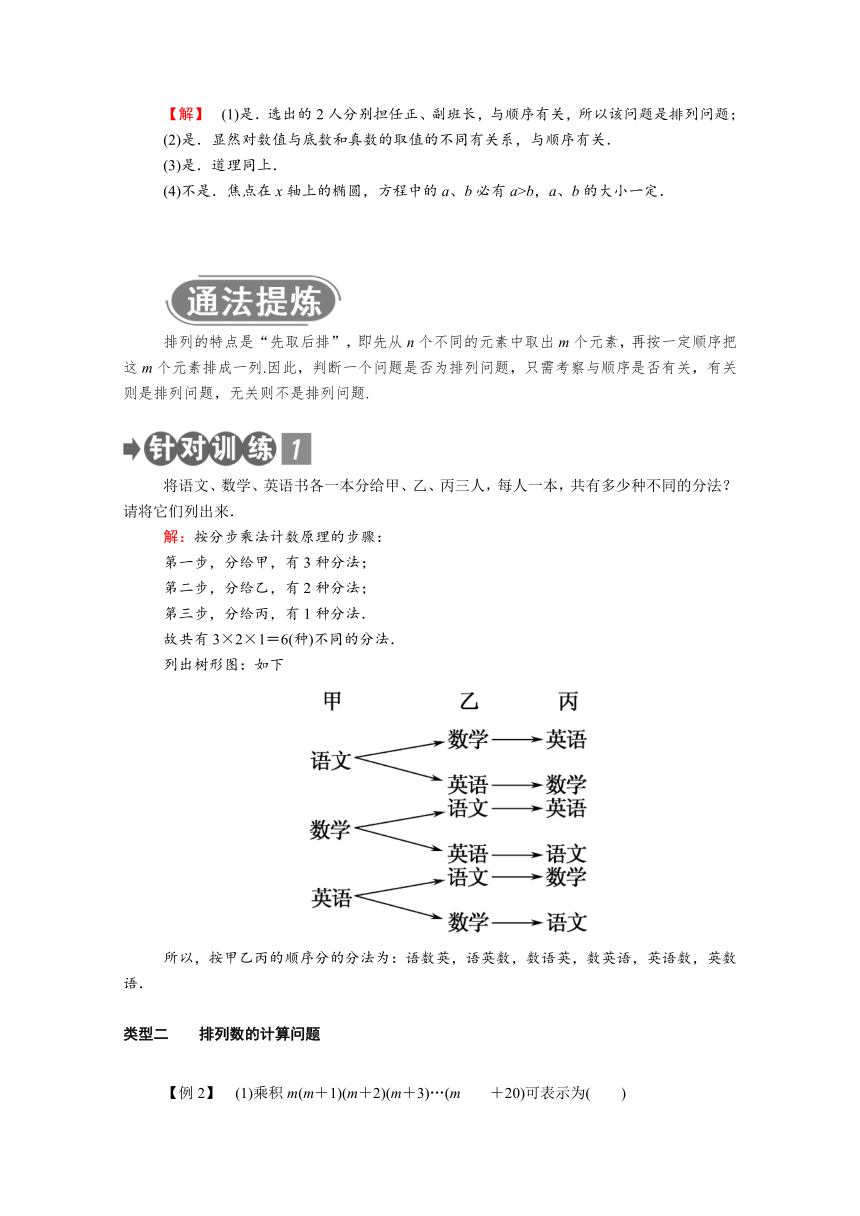
将语文、数学、英语书各一本分给甲、乙、丙三人,每人一本,共有多少种不同的分法?请将它们列出来.
解:按分步乘法计数原理的步骤:
第一步,分给甲,有3种分法;
第二步,分给乙,有2种分法;
第三步,分给丙,有1种分法.
故共有3×2×1=6(种)不同的分法.
列出树形图:如下
所以,按甲乙丙的顺序分的分法为:语数英,语英数,数语英,数英语,英语数,英数语.
类型二 排列数的计算问题
【例2】 (1)乘积m(m+1)(m+2)(m+3)…(m+20)可表示为( )
A.A B.A
C.A D.A
(2)计算:①A;②.
【分析】 按排列数公式计算.
【解析】 (1)因为m,m+1,m+2,…,m+20中最大的数为m+20,且共有m+20-m+1=21个因式.所以m(m+1)·(m+2)…(m+20)=A.
(2)解:①A=15×14×13=2 730.
②方法1:=
==.
方法2:===.
【答案】 (1)D (2)①2 730 ②
1.排列数的计算主要是利用排列数的乘积公式进行,应用时注意:连续正整数的积可以写成某个排列数,其中最大的是排列元素的总个数,而正整数(因式)的个数是选取元素的个数,这是排列数公式的逆用.
2.应用排列数公式的阶乘形式时,一般写出它们的式子后,再提取公因式,然后计算,这样往往会减少运算量.
(1)设x∈N*,且x<23,则(23-x)(24-x)(25-x)·…·(30-x)可化简为( D )
A.A B.A
C.A D.A
解析:本题考查排列数公式的应用.先确定最大数,即n,再确定因式的个数,即m.因为n=30-x,m=(30-x)-(23-x)+1=8,所以原式=A.故选D.
(2)计算的值.
解:==6.
类型三 列举法解决排列问题
【例3】 (1)从1,2,3,4四个数字中任取两个数字组成两位数,共有多少个不同的两位数?
(2)写出从4个元素a,b,c,d中任取3个元素的所有排列.
【解】 (1)由题意作树形图,如图.
故所有两位数为12,13,14,21,23,24,31,32,34,41,42,43,共有12个.
(2)由题意作树形图,如图.
故所有的排列为:abc,abd,acb,acd,adb,adc,bac,bad,bca,bcd,bda,bdc,cab,cad,cba,cbd,cda,cdb,dab,dac,dba,dbc,dca,dcb,共有24个.
“树形图”在解决个数不多的排列问题时,是一种比较有效的表示方式.在操作中先将元素按一定顺序排出,然后以先安排哪个元素为分类标准,进行分类,在每一类中再按余下的元素在前面元素不变的情况下确定第二位元素,再按此元素分类,依次进行,直到完成一个排列,这样能做到不重不漏,然后再按树形图写出排列.
将A,B,C,D四名同学按一定顺序排成一行,要求自左向右,且A不排在第一,B不排在第二,C不排在第三,D不排在第四,试用树形图列出所有可能的排法.
解:树形图为(如图):
由树形图知,所有排法为BADC,BCDA,BDAC,CADB,CDAB,CDBA,DABC,DCAB,DCBA,共有9种排法.
忽视排列问题中的限制条件致误
【例4】 在1,2,3,4的排列a1a2a3a4中,满足a1>a2,a3>a2,a3>a4的排列个数是________.
【错解】 排列的个数是12个或8个.
【错因分析】 3个限制只注意1个限制条件或2个限制条件.
【正解】 首先注意a1位置的数比a2位置的数大,可以借助树形图进行筛选.
满足a1>a2的树形图是:
其次满足a3>a2的树形图是:
再满足a3>a4的排列:2 143,3 142,3 241,4 132,4 231,共5个.
【答案】 5
由1,2,3,4这四个数字组成的首位数字是1,且恰有三个相同数字的四位数的个数是12.
解析:本题要求首位数字是1,且恰有三个相同的数字,用树形图表示为:
由此可知共有12个.
1.下列问题中不属于排列问题的是( B )
A.从六名学生中选三名学生参加数学、物理、化学竞赛,共有多少种选法
B.有十二名学生参加植树活动,要求三人一组,共有多少种分组方案
C.从3,5,7,9中任取两个数做指数运算,可以得到多少个幂
D.从1,2,3,4中任取两个数作为点的坐标,可以得到多少个点
解析:12名学生分为4组,3人一组无先后顺序,不属于排列问题.
2.已知A=132,则n=( B )
A.11 B.12
C.13 D.14
解析:n(n-1)=132,n=12.
3.某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了1_560条毕业留言.(用数字作答)
解析:由题意知两两彼此给对方写一条毕业留言相当于从40人中任选两人的排列数,所以全班共写了A=40×39=1 560条毕业留言.
4.计算:(2A+A)÷(A-A)=2.
5.如果A=10A,求n的值.
解:因为A=2n(2n-1)(2n-2),10A=10n(n-1)(n-2),从而2n(2n-1)(2n-2)=10n(n-1)(n-2).
化简得,n2-9n+8=0.
解得,n=8或n=1(因为n≥3,所以n=1舍去),所以n的值为8.
1.2.1 排列
第1课时 排列与排列数公式
[目标] 1.理解排列和排列数的特征.2.正确运用排列数公式进行计算.
[重点] 理解排列的概念,会用排列数公式进行计算.
[难点] 对排列的有序性的正确理解,排列数公式的逆用.
知识点一 排列的概念
[填一填]
1.排列的定义
一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
2.相同排列
两个排列相同,当且仅当两个排列的元素完全相同,且元素的排列顺序也相同.
[答一答]
1.排列的定义中包括哪两个基本内容?
提示:排列定义包括两个基本内容:一是“取出的元素不能重复”;二是“按照一定的顺序排列”.
2.两个排列若为相同的排列需具备哪些条件?
提示:需要具备两个条件:一是元素完全相同,二是元素的排列顺序完全相同.
3.判断一个具体问题是否为排列问题的关键是什么?
提示:判断一个具体问题是不是排列问题,关键看在安排取出的元素时是有序还是无序,有序就是排列,无序就不是排列.
知识点二 排列数公式
[填一填]
[答一答]
4.“排列数”与“一个排列”是否为同一个概念?
提示:不是同一概念.“一个排列”是指“从n个不同元素中取出m个元素,按照一定的顺序排成一列”,它不是一个数;“排列数”是指“从n个不同元素中取出m个元素的所有排列的个数”.例如,从a,b,c中任取2个元素的排列有ab,ba,ac,ca,bc,cb,共6个,6就是从a,b,c中任取2个元素的排列数.
5.对于排列数A中,m,n有什么要求?
提示:m、n∈N+,且m≤n.
6.在A=n(n-1)…(n-m+1)中右边共多少项的乘积.
提示:从n,(n-1),…,(n-m+1)以上m个数相乘,可得共m项.
7.为什么规定0!=1?
提示:为了使公式A=在m=n时也能成立,规定0!=1,这种规定说明:若一个元素都不取,则构成排列的情形只有1种.
1.对排列定义的四点说明
(1)定义的两个要素:
一是“从n个不同元素中取出m(m≤n)个元素”,要求取出的元素不能重复;二是“按照一定的顺序排列”.
(2)定义中“一定顺序”就是说与位置有关,选取的元素相同但顺序不同是不同的排列,在实际问题中,要由具体问题的性质和条件决定.
(3)对于两个排列,只有各元素完全相同,并且元素的排列顺序也完全相同时,才是相同排列.
(4)在定义中规定m≤n,如果m
(1)公式中的n,m应该满足n,m∈N*,m≤n,当m>n时不成立.
(2)排列数有两个公式,第一个公式右边是若干数的连乘积,其特点是:第一个因数是n(下标),后面的每一个因数都比它前面的因数少1,最后一个因数为n-m+1(下标-上标+1),共有m(上标)个连续自然数相乘.
(3)排列数的第二个公式是阶乘的形式,所以又叫排列数的阶乘式,它是一个分式的形式,分子是下标n的阶乘,分母是下标减上标的阶乘,即(n-m)的阶乘,
(4)特别地,规定0!=1.这只是一种规定,不能按阶乘的含义作解释.
类型一 排列的概念
【例1】 判断下列问题是否是排列问题:
(1)某班共有50名同学,现要投票选举正、副班长各一人,共有多少种可能的选举结果?
(2)从2,3,5,7,9中任取两数分别作对数的底数和真数,有多少不同对数值?
(3)从1到10十个自然数中任取两个数组成点的坐标,可得多少个不同的点的坐标?
(4)从集合M={1,2,…,9}中,任取相异的两个元素作为a,b,可以得到多少个焦点在x轴上的椭圆方程+=1?
【分析】 由题目可获取以下主要信息:
对于(1),两人当班长,有正副之分;
对于(2),对数的底数与真数交换,其值也不同;
对于(3),点的坐标有横坐标与纵坐标之分;
对于(4),焦点在x轴上的椭圆方程,必须a>b.
解答本题,其关键是看问题的结果与选出的元素排列时跟顺序是否有关,有关即是排列问题,否则不是.
【解】 (1)是.选出的2人分别担任正、副班长,与顺序有关,所以该问题是排列问题;
(2)是.显然对数值与底数和真数的取值的不同有关系,与顺序有关.
(3)是.道理同上.
(4)不是.焦点在x轴上的椭圆,方程中的a、b必有a>b,a、b的大小一定.
排列的特点是“先取后排”,即先从n个不同的元素中取出m个元素,再按一定顺序把这m个元素排成一列.因此,判断一个问题是否为排列问题,只需考察与顺序是否有关,有关则是排列问题,无关则不是排列问题.
将语文、数学、英语书各一本分给甲、乙、丙三人,每人一本,共有多少种不同的分法?请将它们列出来.
解:按分步乘法计数原理的步骤:
第一步,分给甲,有3种分法;
第二步,分给乙,有2种分法;
第三步,分给丙,有1种分法.
故共有3×2×1=6(种)不同的分法.
列出树形图:如下
所以,按甲乙丙的顺序分的分法为:语数英,语英数,数语英,数英语,英语数,英数语.
类型二 排列数的计算问题
【例2】 (1)乘积m(m+1)(m+2)(m+3)…(m+20)可表示为( )
A.A B.A
C.A D.A
(2)计算:①A;②.
【分析】 按排列数公式计算.
【解析】 (1)因为m,m+1,m+2,…,m+20中最大的数为m+20,且共有m+20-m+1=21个因式.所以m(m+1)·(m+2)…(m+20)=A.
(2)解:①A=15×14×13=2 730.
②方法1:=
==.
方法2:===.
【答案】 (1)D (2)①2 730 ②
1.排列数的计算主要是利用排列数的乘积公式进行,应用时注意:连续正整数的积可以写成某个排列数,其中最大的是排列元素的总个数,而正整数(因式)的个数是选取元素的个数,这是排列数公式的逆用.
2.应用排列数公式的阶乘形式时,一般写出它们的式子后,再提取公因式,然后计算,这样往往会减少运算量.
(1)设x∈N*,且x<23,则(23-x)(24-x)(25-x)·…·(30-x)可化简为( D )
A.A B.A
C.A D.A
解析:本题考查排列数公式的应用.先确定最大数,即n,再确定因式的个数,即m.因为n=30-x,m=(30-x)-(23-x)+1=8,所以原式=A.故选D.
(2)计算的值.
解:==6.
类型三 列举法解决排列问题
【例3】 (1)从1,2,3,4四个数字中任取两个数字组成两位数,共有多少个不同的两位数?
(2)写出从4个元素a,b,c,d中任取3个元素的所有排列.
【解】 (1)由题意作树形图,如图.
故所有两位数为12,13,14,21,23,24,31,32,34,41,42,43,共有12个.
(2)由题意作树形图,如图.
故所有的排列为:abc,abd,acb,acd,adb,adc,bac,bad,bca,bcd,bda,bdc,cab,cad,cba,cbd,cda,cdb,dab,dac,dba,dbc,dca,dcb,共有24个.
“树形图”在解决个数不多的排列问题时,是一种比较有效的表示方式.在操作中先将元素按一定顺序排出,然后以先安排哪个元素为分类标准,进行分类,在每一类中再按余下的元素在前面元素不变的情况下确定第二位元素,再按此元素分类,依次进行,直到完成一个排列,这样能做到不重不漏,然后再按树形图写出排列.
将A,B,C,D四名同学按一定顺序排成一行,要求自左向右,且A不排在第一,B不排在第二,C不排在第三,D不排在第四,试用树形图列出所有可能的排法.
解:树形图为(如图):
由树形图知,所有排法为BADC,BCDA,BDAC,CADB,CDAB,CDBA,DABC,DCAB,DCBA,共有9种排法.
忽视排列问题中的限制条件致误
【例4】 在1,2,3,4的排列a1a2a3a4中,满足a1>a2,a3>a2,a3>a4的排列个数是________.
【错解】 排列的个数是12个或8个.
【错因分析】 3个限制只注意1个限制条件或2个限制条件.
【正解】 首先注意a1位置的数比a2位置的数大,可以借助树形图进行筛选.
满足a1>a2的树形图是:
其次满足a3>a2的树形图是:
再满足a3>a4的排列:2 143,3 142,3 241,4 132,4 231,共5个.
【答案】 5
由1,2,3,4这四个数字组成的首位数字是1,且恰有三个相同数字的四位数的个数是12.
解析:本题要求首位数字是1,且恰有三个相同的数字,用树形图表示为:
由此可知共有12个.
1.下列问题中不属于排列问题的是( B )
A.从六名学生中选三名学生参加数学、物理、化学竞赛,共有多少种选法
B.有十二名学生参加植树活动,要求三人一组,共有多少种分组方案
C.从3,5,7,9中任取两个数做指数运算,可以得到多少个幂
D.从1,2,3,4中任取两个数作为点的坐标,可以得到多少个点
解析:12名学生分为4组,3人一组无先后顺序,不属于排列问题.
2.已知A=132,则n=( B )
A.11 B.12
C.13 D.14
解析:n(n-1)=132,n=12.
3.某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了1_560条毕业留言.(用数字作答)
解析:由题意知两两彼此给对方写一条毕业留言相当于从40人中任选两人的排列数,所以全班共写了A=40×39=1 560条毕业留言.
4.计算:(2A+A)÷(A-A)=2.
5.如果A=10A,求n的值.
解:因为A=2n(2n-1)(2n-2),10A=10n(n-1)(n-2),从而2n(2n-1)(2n-2)=10n(n-1)(n-2).
化简得,n2-9n+8=0.
解得,n=8或n=1(因为n≥3,所以n=1舍去),所以n的值为8.
