安徽省淮北市树人高级中学2020-2021学年高一下学期开学考试数学试卷 Word版含答案
文档属性
| 名称 | 安徽省淮北市树人高级中学2020-2021学年高一下学期开学考试数学试卷 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 09:30:50 | ||
图片预览




文档简介
2020—2021第二学期高一数学开学考试卷
时间:120分钟 满分:150分
一、单项选择题(本大题共12小题,共60.0分)
已知命题p:,,则它的否定形式为
A. , B. ,
C. , D. ,
函数的零点所在的区间是
A. B. C. D.
下列四组函数中,表示相等函数的一组是
A. , B. ,
C. , D. ,
已知为常数,那么函数的图象不可能是
A. B.
C. D.
下列说法正确的是
A. 为了解我国中学生课外阅读的情况,应采取全面调查的方式
B. 一组数据1、2、5、5、5、3、3的中位数和众数都是5
C. 投掷一枚硬币100次,一定有50次“正面朝上”
D. 若甲组数据的方差是,乙组数据的方差是,则甲组数据比乙组数据稳定
已知,则a,b,c的大小关系是
A. B. C. D.
点P从出发,沿单位圆逆时针方向运动弧长到达点Q,则点Q的坐标为
A. B. C. D.
已知是R上的奇函数且,当时,,
A. B. 2 C. D. 98
,满足对任意,都有成立,那么a的取值范围是
A. B. C. D.
已知函数,则的最大值为
A. B. C. 0 D. 1
已知,则
A. B. C. D.
已知在上是增函数,则实数a的取值范围是
A. B.
C. , D.
二、填空题(本大题共4小题,共20.0分)
已知半径为r的扇形OAB的面积为1,周长为4,则 ______ .
若函数,满足,且,则 ______ .
甲、乙两人同时参加环保知识晋级赛,甲晋级的概率为,乙晋级的概率为,两人是否晋级互不影响,则其中至少有一人晋级的概率为________.
若命题“,”是假命题,则实数a的取值范围是______ .
三、解答题(本大题共6小题,共70.0分)
在平面直角坐标系xOy中,角的顶点为O,始边为x轴的正半轴,终边经过点,且.
求实数m的值;求?的值.
18.已知二次函数在上的最小值为0,设.
求a的值;
当时,求函数的值域;
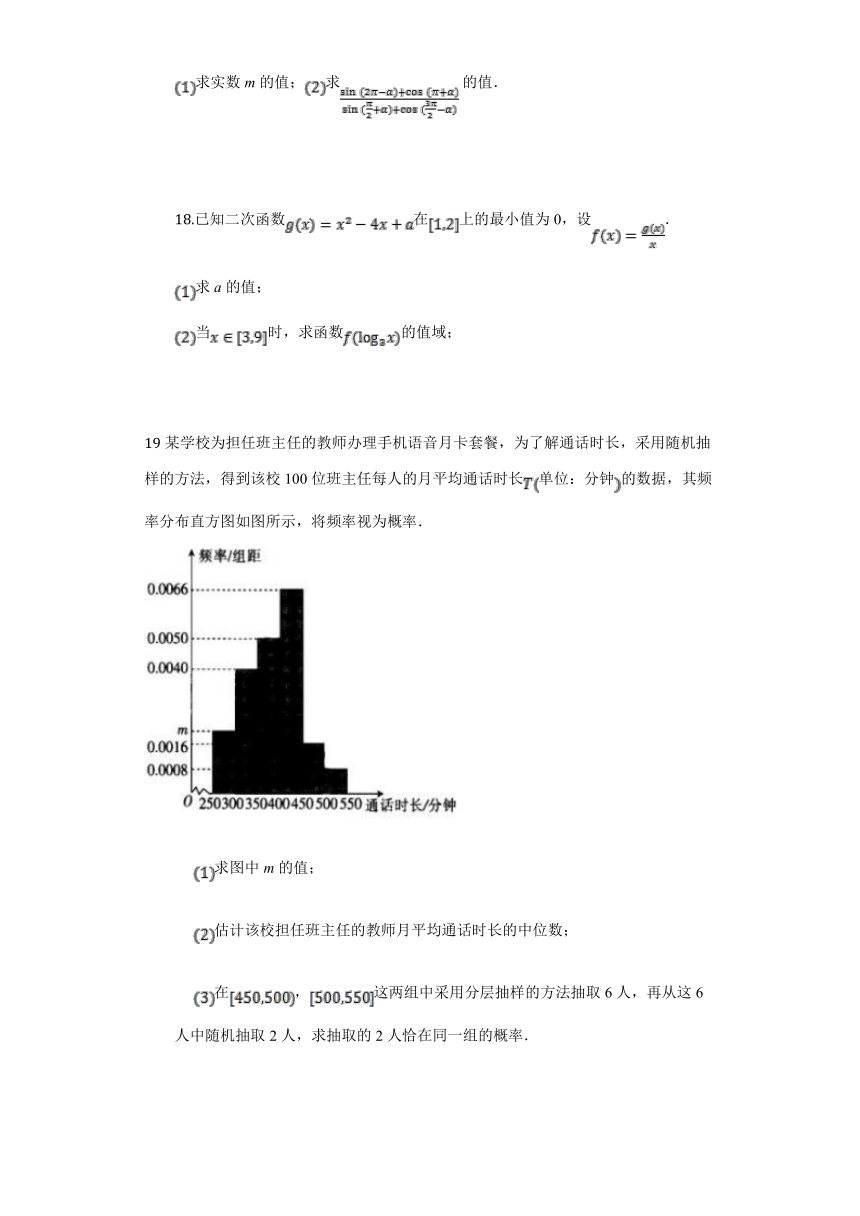
19某学校为担任班主任的教师办理手机语音月卡套餐,为了解通话时长,采用随机抽样的方法,得到该校100位班主任每人的月平均通话时长单位:分钟的数据,其频率分布直方图如图所示,将频率视为概率.
??? 求图中m的值;
??? 估计该校担任班主任的教师月平均通话时长的中位数;
在,这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.
20.已知函数为奇函数.
求a的值,并用函数单调性的定义证明函数在R上是增函数;
求不等式十的解集.
21. 2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.为降低疫情影响,某厂家拟尽快加大力度促进生产.已知该厂家生产某种产品的年固定成本为200万元,每生产x千件,需另投入成本为,当年产量不足80千件时,万元当年产量不小于80千件时,万元每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.
写出年利润万元关于年产量千件的函数解析式;
当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?最大利润是多少?
22.已知函数,.
Ⅰ当时,写出的单调递减区间不必证明,并求的值域;
Ⅱ设函数,若对任意,总有,使得,求实数t的取值范围.
2020—2021第二学期高一数学开学考试答案
【答案】
1. D 2. B 3. A 4. B 5. D 6. A 7. A
8. A 9. C 10. D 11. A 12. B
13. 1??
14. 9??
15. ??
16. ??
17. 解:由于角的终边经过点,且,
所以,且,
从而,即,
解得.
由知,
所以,
所以
.
??
18. 解:,
故当时,取最小值0,
则,
解得.
,
令,,则,
则在上单调递减,
则,,
所以值域为.??
19. 解:依题意,,
解得.
设该校担任班主任的教师月平均通话时长的中位数为t.
因为前2组的频率之和为,
前3组的频率之和为,
所以,由,得.
所以该校担任班主任的教师月平均通话时长的中位数为390分钟.
在内抽取人,记为a,b,c,d,
在内抽取2人,记为e,f,
则6人中抽取2人的取法有:
,,,,,,,,,
,,,,,,共15种等可能的取法.
其中抽取的2人恰在同一组的有:
,,,,,,,共7种取法,
所以从这6人中随机抽取的2人恰在同一组的概率.??
20. 解:是奇函数,
,则,,
证明:设,则,
由,可得,则,
,即,
在R上是增函数.
由可知为单调递增的奇函数,
不等式可化为,
,即,解得,
故不等式的解集.??
21. 解:每件商品售价为万元,则x千件商品销售额为万元,
依题意得:
当时,,
当时,.
;
当时,,
此时,当时,即万元;
当时,,
当且仅当,即时,即万元.
由于,
当年产量为30千件时,该厂在这一商品生产中所获利润最大,最大利润为250万元.??
22. 解:Ⅰ当时,,
的单调递减区间为,单调递增区间为,
当时,,
当且仅当,即时取等号,
当时,
当且仅当,即时取等号,
故函数的值域为;
Ⅱ函数,
当时,,所以,
设函数在上的值域为A,
因为对任意,总有,使得,
所以,
又,,
故,
解得,
当时,在上单调递增,
则有,
可得,解得,
所以;
当时,,当且仅当时取等号,
当,即时,在上单调递减,
所以,
可得,解得,
所以;
当,即时,,
所以,
,解得,
所以;
当,即时,,
所以,
可得,解得,
所以;
综上可得,t的取值范围为.
时间:120分钟 满分:150分
一、单项选择题(本大题共12小题,共60.0分)
已知命题p:,,则它的否定形式为
A. , B. ,
C. , D. ,
函数的零点所在的区间是
A. B. C. D.
下列四组函数中,表示相等函数的一组是
A. , B. ,
C. , D. ,
已知为常数,那么函数的图象不可能是
A. B.
C. D.
下列说法正确的是
A. 为了解我国中学生课外阅读的情况,应采取全面调查的方式
B. 一组数据1、2、5、5、5、3、3的中位数和众数都是5
C. 投掷一枚硬币100次,一定有50次“正面朝上”
D. 若甲组数据的方差是,乙组数据的方差是,则甲组数据比乙组数据稳定
已知,则a,b,c的大小关系是
A. B. C. D.
点P从出发,沿单位圆逆时针方向运动弧长到达点Q,则点Q的坐标为
A. B. C. D.
已知是R上的奇函数且,当时,,
A. B. 2 C. D. 98
,满足对任意,都有成立,那么a的取值范围是
A. B. C. D.
已知函数,则的最大值为
A. B. C. 0 D. 1
已知,则
A. B. C. D.
已知在上是增函数,则实数a的取值范围是
A. B.
C. , D.
二、填空题(本大题共4小题,共20.0分)
已知半径为r的扇形OAB的面积为1,周长为4,则 ______ .
若函数,满足,且,则 ______ .
甲、乙两人同时参加环保知识晋级赛,甲晋级的概率为,乙晋级的概率为,两人是否晋级互不影响,则其中至少有一人晋级的概率为________.
若命题“,”是假命题,则实数a的取值范围是______ .
三、解答题(本大题共6小题,共70.0分)
在平面直角坐标系xOy中,角的顶点为O,始边为x轴的正半轴,终边经过点,且.
求实数m的值;求?的值.
18.已知二次函数在上的最小值为0,设.
求a的值;
当时,求函数的值域;
19某学校为担任班主任的教师办理手机语音月卡套餐,为了解通话时长,采用随机抽样的方法,得到该校100位班主任每人的月平均通话时长单位:分钟的数据,其频率分布直方图如图所示,将频率视为概率.
??? 求图中m的值;
??? 估计该校担任班主任的教师月平均通话时长的中位数;
在,这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.
20.已知函数为奇函数.
求a的值,并用函数单调性的定义证明函数在R上是增函数;
求不等式十的解集.
21. 2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.为降低疫情影响,某厂家拟尽快加大力度促进生产.已知该厂家生产某种产品的年固定成本为200万元,每生产x千件,需另投入成本为,当年产量不足80千件时,万元当年产量不小于80千件时,万元每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.
写出年利润万元关于年产量千件的函数解析式;
当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?最大利润是多少?
22.已知函数,.
Ⅰ当时,写出的单调递减区间不必证明,并求的值域;
Ⅱ设函数,若对任意,总有,使得,求实数t的取值范围.
2020—2021第二学期高一数学开学考试答案
【答案】
1. D 2. B 3. A 4. B 5. D 6. A 7. A
8. A 9. C 10. D 11. A 12. B
13. 1??
14. 9??
15. ??
16. ??
17. 解:由于角的终边经过点,且,
所以,且,
从而,即,
解得.
由知,
所以,
所以
.
??
18. 解:,
故当时,取最小值0,
则,
解得.
,
令,,则,
则在上单调递减,
则,,
所以值域为.??
19. 解:依题意,,
解得.
设该校担任班主任的教师月平均通话时长的中位数为t.
因为前2组的频率之和为,
前3组的频率之和为,
所以,由,得.
所以该校担任班主任的教师月平均通话时长的中位数为390分钟.
在内抽取人,记为a,b,c,d,
在内抽取2人,记为e,f,
则6人中抽取2人的取法有:
,,,,,,,,,
,,,,,,共15种等可能的取法.
其中抽取的2人恰在同一组的有:
,,,,,,,共7种取法,
所以从这6人中随机抽取的2人恰在同一组的概率.??
20. 解:是奇函数,
,则,,
证明:设,则,
由,可得,则,
,即,
在R上是增函数.
由可知为单调递增的奇函数,
不等式可化为,
,即,解得,
故不等式的解集.??
21. 解:每件商品售价为万元,则x千件商品销售额为万元,
依题意得:
当时,,
当时,.
;
当时,,
此时,当时,即万元;
当时,,
当且仅当,即时,即万元.
由于,
当年产量为30千件时,该厂在这一商品生产中所获利润最大,最大利润为250万元.??
22. 解:Ⅰ当时,,
的单调递减区间为,单调递增区间为,
当时,,
当且仅当,即时取等号,
当时,
当且仅当,即时取等号,
故函数的值域为;
Ⅱ函数,
当时,,所以,
设函数在上的值域为A,
因为对任意,总有,使得,
所以,
又,,
故,
解得,
当时,在上单调递增,
则有,
可得,解得,
所以;
当时,,当且仅当时取等号,
当,即时,在上单调递减,
所以,
可得,解得,
所以;
当,即时,,
所以,
,解得,
所以;
当,即时,,
所以,
可得,解得,
所以;
综上可得,t的取值范围为.
同课章节目录
