2020-2021学年人教版八年级数学下册 第十八章 平行四边形 综合训练试卷(Word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册 第十八章 平行四边形 综合训练试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 299.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 07:31:50 | ||
图片预览



文档简介
2020——2021学年度人教版八年级数学下册
第十八章
平行四边形
综合训练题
一、选择题
1.平行四边形两邻边分别为24和16,则平行四边形周长为(
)
A.20
B.40
C.60
D.80
2.菱形ABCD的对角线AC=6,BD=8,那么边AB的长度
是(
)
A.10
B.5
C.
D.
3.下列说法正确的是(
)
A.对角线相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是矩形
D.对角线互相垂直平分且相等的四边形是正方形
4.下列四个命题中,真命题是(
)
A.对角线互相垂直的四边形是菱形
B.对角线互相平分且垂直的四边形是矩形
C.顺次连接矩形四边中点得到的四边形是菱形
D.对角线互相垂直相等的四边形是正方形
5.矩形ABCD的对角线AC、BD相交于点O,AB=4cm,∠AOB=60°,则这个矩形的对角线长是( )
A.2cm
B.4cm
C.6cm
D.8cm
6.已知四边形ABCD中,AB∥CD,添加下列条件仍不能判断四边形ABCD是平行四边形的是(
)
A.AB=CD
B.AD=BC
C.AD∥BC
D.∠A+∠B=180°
7.要判断一个四边形是否为矩形,下面是4位同学拟定的方案,其中正确的是
(
)
A.测量两组对边是否分别相等
B.测量两条对角线是否互相垂直平分
C.测量其中三个内角是作都为直角
D.测量两条对角线是否相等
8.下列说法:①一组对边平行且另一组对边相等的四边形是平行四边形;②两条对角线相等的四边形是矩形;③顺次连接菱形四边中点所得到的四边形是矩形;④四个角都相等的四边形是矩形;⑤平行四边形对角线的交点到一组对边的距离相等.正确的有(
)个
A.2
B.3
C.4
D.5
9.如图,、分别是平行四边形的边、上的点,、交于点,请你添加一个条件,使四边形是平行四边形,下列选项中不能推断四边形是平行四边形的是(
)
A.
B.
C.
D.
10.如图,正方形的边长为2,是的中点,,与交于点,则的长为(
)
A.
B.
C.
D.3
二、填空题
11.如图,在直线AP上方有一个正方形ABCD,∠PAD=30°,以点B为圆心,AB长为半径作弧,与AP交于点A,M,分别以点A,M为圆心,AM长为半径作弧,两弧交于点E,连接ED,则∠ADE的度数为_____.
12.如图,菱形ABCD的对角线AC,BD相交于点O,已知OB=4,菱形ABCD的面积为24,则AC的长为_____
13.如图,是的对角线交点,为中点,交于点,若.则的值为__________.
14.如图,在边长为的正方形中,E、F分别是边、上的点.若,,则的长为______.
15.如图,将矩形沿折叠,点落在点处,点落在边上的点处,若,则等于___.
三、解答题
16.如图,为边的中点,交的延长线于点,连接,平分,求证:四边形为菱形.
17.如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:
(1)AE=CF;
(2)四边形AECF是平行四边形.
18.如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
(1)求证:四边形AMDN是平行四边形;
(2)在点M移动过程中:①当四边形AMDN成矩形时,求此时AM的长;
②当四边形AMDN成菱形时,求此时AM的长.
19.如图,四边形是菱形,,交的延长线于点,,交的延长线于点,求证:.
20.如图,ABCD是矩形纸片,翻折∠B,∠D,使BC,AD恰好落在AC上.设F,H分别是B,D落在AC上的两点,E,G分别是折痕CE,AG与AB,CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
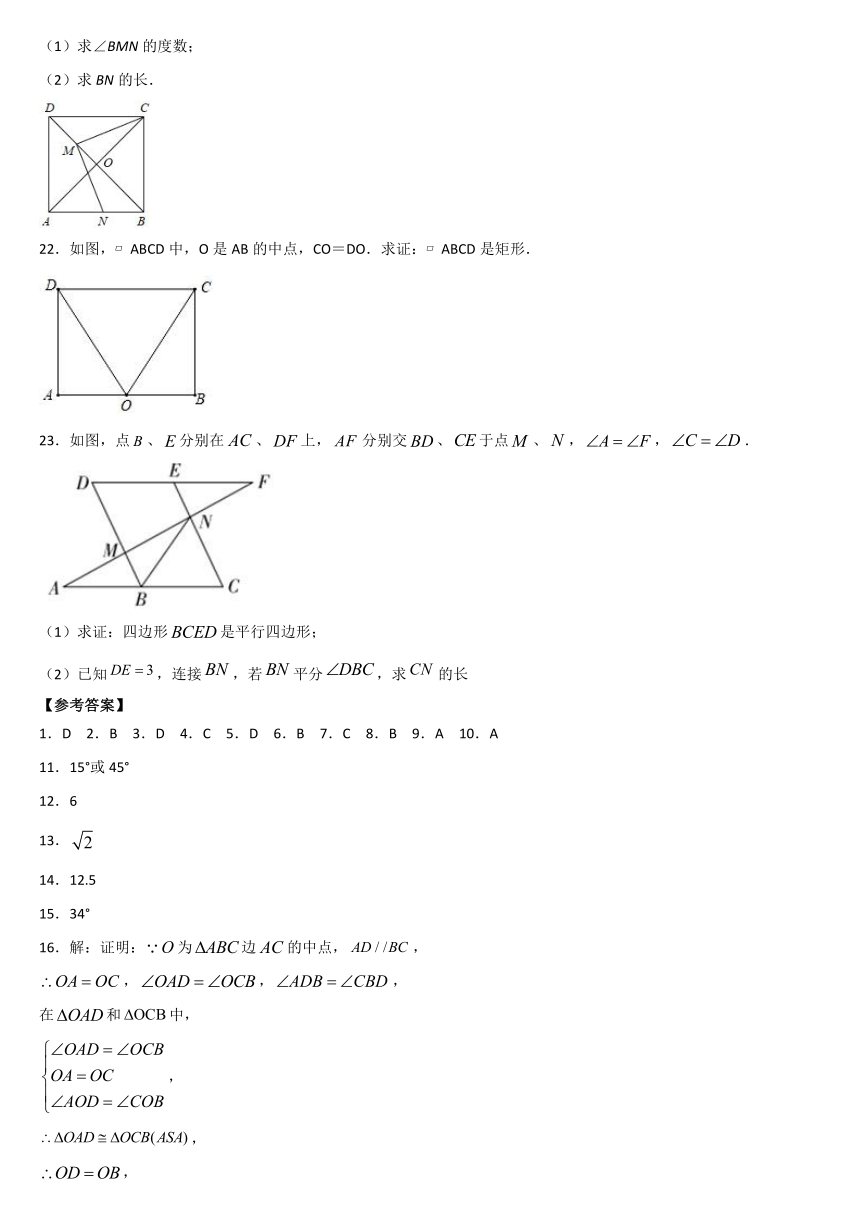
21.如图,已知正方形ABCD的面积是8,连接AC、BD交于点O,CM平分∠ACD交BD于点M,MN⊥CM,交AB于点N,
(1)求∠BMN的度数;
(2)求BN的长.
22.如图,?ABCD中,O是AB的中点,CO=DO.求证:?ABCD是矩形.
23.如图,点、分别在、上,分别交、于点、,,.
(1)求证:四边形是平行四边形;
(2)已知,连接,若平分,求的长
【参考答案】
1.D
2.B
3.D
4.C
5.D
6.B
7.C
8.B
9.A
10.A
11.15°或45°
12.6
13.
14.12.5
15.34°
16.解:证明:为边的中点,,
,,,
在和中,
,
,
,
四边形是平行四边形,
平分,
,
,
,
四边形是菱形.
17.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
在△ADE和△CBF中,
,
∴(AAS),
∴AE=CF.
(2)∵AE⊥BD,CF⊥BD,
∴AE∥CF,
由(1)得AE=CF,
∴四边形AECF是平行四边形.
18.解:(1)∵四边形ABCD是菱形,
∴AB=CD=AD=2,AB∥CD,
∴∠NDA=∠DAM,
∵点E是AD边的中点,
∴AE=DE,且∠NDA=∠DAM,∠NED=∠AEM,
∴,
∴DN=AM,
又∵NC∥AB,
∴四边形AMDN是平行四边形.
(2)①若四边形AMDN成矩形时,则DM⊥AB,
在中,DM⊥AB,∠DAB=60°,AD=2,
∴AM=1,
∴当AM=1时,四边形AMDN成矩形.
②若四边形AMDN成菱形,则DM=AM,
∵DM=AM,∠DAB=60°,
∴为等边三角形,
∴AM=AD=2,
∴当AM=2时,四边形AMDN成菱形.
19.证明:∵四边形是菱形,
∴,,
∴,,
∴
∵,,
∴
∴,
∴
20.(1)证明:在矩形ABCD中,
∵AD∥BC,
∴∠DAC=∠BCA.
由题意,得∠GAH=∠DAC,∠ECF=∠BCA.
∴∠GAH=∠ECF,
∴AG∥CE.
又∵AE∥CG,
∴四边形AECG是平行四边形.
(2)在Rt△ABC中,
∵AB=4,BC=3,
∴AC=5.
∵CF=CB=3,
∴AF=2.
在Rt△AEF中,
设EF=x,则AE=4﹣x.
根据勾股定理,得AE2=AF2+EF2,
即(4﹣x)2=22+x2.
解得x=,即线段EF长为cm.
21.解:(1)∵正方形ABCD的面积是8,
∴BC=CD==2,
∴BD=×2=4.
∵四边形ABCD为正方形,
∴∠DCO=∠BCO=∠CDO=∠MBN=45°,
∵CM平分∠ACD,
∴∠DCM=∠MCO=22.5°,
∴∠BMC=∠CDO+∠DCM=45°+22.5°=67.5°.
∵MN⊥CM,
∴∠CMN=90°,
∴∠BMN=90°﹣67.5°=22.5°,
∴∠BMN的度数为22..5°.
(2)∵∠MCO=22.5°,∠BCO=45°,
∴∠BCM=∠BCO+∠MCO=67.5°,
又∵∠BMC=67.5°,
∴∠BCM=∠BMC,
∴BM=BC=CD=2,
∴DM=BD﹣BM=4﹣2.
∵∠DCM=22.5°,∠BMN=22.5°,
∴∠DCM=∠BMN.
∴在△DCM和△BMN中,
∴△DCM≌△BMN(ASA),
∴BN=DM=4﹣2,
∴BN的长为4﹣2.
22.证明:∵四边形ABCD是平行四边形,
∴AD=BC,ADBC,
∴∠A+∠B=180°,
∵O是AB的中点,
∴AO=BO,
在△DAO和△CBO中,,
∴△DAO≌△CBO(SSS),
∴∠A=∠B,
∵∠A+∠B=180°,
∴∠A=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
23.(1)∵,
∴,,
又∵,
∴,
∴,
∴四边形是平行四边形;
(2)∵平分,
∴,
∵,
∴,
∴,
∴,
又∵,
∴
第十八章
平行四边形
综合训练题
一、选择题
1.平行四边形两邻边分别为24和16,则平行四边形周长为(
)
A.20
B.40
C.60
D.80
2.菱形ABCD的对角线AC=6,BD=8,那么边AB的长度
是(
)
A.10
B.5
C.
D.
3.下列说法正确的是(
)
A.对角线相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是矩形
D.对角线互相垂直平分且相等的四边形是正方形
4.下列四个命题中,真命题是(
)
A.对角线互相垂直的四边形是菱形
B.对角线互相平分且垂直的四边形是矩形
C.顺次连接矩形四边中点得到的四边形是菱形
D.对角线互相垂直相等的四边形是正方形
5.矩形ABCD的对角线AC、BD相交于点O,AB=4cm,∠AOB=60°,则这个矩形的对角线长是( )
A.2cm
B.4cm
C.6cm
D.8cm
6.已知四边形ABCD中,AB∥CD,添加下列条件仍不能判断四边形ABCD是平行四边形的是(
)
A.AB=CD
B.AD=BC
C.AD∥BC
D.∠A+∠B=180°
7.要判断一个四边形是否为矩形,下面是4位同学拟定的方案,其中正确的是
(
)
A.测量两组对边是否分别相等
B.测量两条对角线是否互相垂直平分
C.测量其中三个内角是作都为直角
D.测量两条对角线是否相等
8.下列说法:①一组对边平行且另一组对边相等的四边形是平行四边形;②两条对角线相等的四边形是矩形;③顺次连接菱形四边中点所得到的四边形是矩形;④四个角都相等的四边形是矩形;⑤平行四边形对角线的交点到一组对边的距离相等.正确的有(
)个
A.2
B.3
C.4
D.5
9.如图,、分别是平行四边形的边、上的点,、交于点,请你添加一个条件,使四边形是平行四边形,下列选项中不能推断四边形是平行四边形的是(
)
A.
B.
C.
D.
10.如图,正方形的边长为2,是的中点,,与交于点,则的长为(
)
A.
B.
C.
D.3
二、填空题
11.如图,在直线AP上方有一个正方形ABCD,∠PAD=30°,以点B为圆心,AB长为半径作弧,与AP交于点A,M,分别以点A,M为圆心,AM长为半径作弧,两弧交于点E,连接ED,则∠ADE的度数为_____.
12.如图,菱形ABCD的对角线AC,BD相交于点O,已知OB=4,菱形ABCD的面积为24,则AC的长为_____
13.如图,是的对角线交点,为中点,交于点,若.则的值为__________.
14.如图,在边长为的正方形中,E、F分别是边、上的点.若,,则的长为______.
15.如图,将矩形沿折叠,点落在点处,点落在边上的点处,若,则等于___.
三、解答题
16.如图,为边的中点,交的延长线于点,连接,平分,求证:四边形为菱形.
17.如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:
(1)AE=CF;
(2)四边形AECF是平行四边形.
18.如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
(1)求证:四边形AMDN是平行四边形;
(2)在点M移动过程中:①当四边形AMDN成矩形时,求此时AM的长;
②当四边形AMDN成菱形时,求此时AM的长.
19.如图,四边形是菱形,,交的延长线于点,,交的延长线于点,求证:.
20.如图,ABCD是矩形纸片,翻折∠B,∠D,使BC,AD恰好落在AC上.设F,H分别是B,D落在AC上的两点,E,G分别是折痕CE,AG与AB,CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
21.如图,已知正方形ABCD的面积是8,连接AC、BD交于点O,CM平分∠ACD交BD于点M,MN⊥CM,交AB于点N,
(1)求∠BMN的度数;
(2)求BN的长.
22.如图,?ABCD中,O是AB的中点,CO=DO.求证:?ABCD是矩形.
23.如图,点、分别在、上,分别交、于点、,,.
(1)求证:四边形是平行四边形;
(2)已知,连接,若平分,求的长
【参考答案】
1.D
2.B
3.D
4.C
5.D
6.B
7.C
8.B
9.A
10.A
11.15°或45°
12.6
13.
14.12.5
15.34°
16.解:证明:为边的中点,,
,,,
在和中,
,
,
,
四边形是平行四边形,
平分,
,
,
,
四边形是菱形.
17.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
在△ADE和△CBF中,
,
∴(AAS),
∴AE=CF.
(2)∵AE⊥BD,CF⊥BD,
∴AE∥CF,
由(1)得AE=CF,
∴四边形AECF是平行四边形.
18.解:(1)∵四边形ABCD是菱形,
∴AB=CD=AD=2,AB∥CD,
∴∠NDA=∠DAM,
∵点E是AD边的中点,
∴AE=DE,且∠NDA=∠DAM,∠NED=∠AEM,
∴,
∴DN=AM,
又∵NC∥AB,
∴四边形AMDN是平行四边形.
(2)①若四边形AMDN成矩形时,则DM⊥AB,
在中,DM⊥AB,∠DAB=60°,AD=2,
∴AM=1,
∴当AM=1时,四边形AMDN成矩形.
②若四边形AMDN成菱形,则DM=AM,
∵DM=AM,∠DAB=60°,
∴为等边三角形,
∴AM=AD=2,
∴当AM=2时,四边形AMDN成菱形.
19.证明:∵四边形是菱形,
∴,,
∴,,
∴
∵,,
∴
∴,
∴
20.(1)证明:在矩形ABCD中,
∵AD∥BC,
∴∠DAC=∠BCA.
由题意,得∠GAH=∠DAC,∠ECF=∠BCA.
∴∠GAH=∠ECF,
∴AG∥CE.
又∵AE∥CG,
∴四边形AECG是平行四边形.
(2)在Rt△ABC中,
∵AB=4,BC=3,
∴AC=5.
∵CF=CB=3,
∴AF=2.
在Rt△AEF中,
设EF=x,则AE=4﹣x.
根据勾股定理,得AE2=AF2+EF2,
即(4﹣x)2=22+x2.
解得x=,即线段EF长为cm.
21.解:(1)∵正方形ABCD的面积是8,
∴BC=CD==2,
∴BD=×2=4.
∵四边形ABCD为正方形,
∴∠DCO=∠BCO=∠CDO=∠MBN=45°,
∵CM平分∠ACD,
∴∠DCM=∠MCO=22.5°,
∴∠BMC=∠CDO+∠DCM=45°+22.5°=67.5°.
∵MN⊥CM,
∴∠CMN=90°,
∴∠BMN=90°﹣67.5°=22.5°,
∴∠BMN的度数为22..5°.
(2)∵∠MCO=22.5°,∠BCO=45°,
∴∠BCM=∠BCO+∠MCO=67.5°,
又∵∠BMC=67.5°,
∴∠BCM=∠BMC,
∴BM=BC=CD=2,
∴DM=BD﹣BM=4﹣2.
∵∠DCM=22.5°,∠BMN=22.5°,
∴∠DCM=∠BMN.
∴在△DCM和△BMN中,
∴△DCM≌△BMN(ASA),
∴BN=DM=4﹣2,
∴BN的长为4﹣2.
22.证明:∵四边形ABCD是平行四边形,
∴AD=BC,ADBC,
∴∠A+∠B=180°,
∵O是AB的中点,
∴AO=BO,
在△DAO和△CBO中,,
∴△DAO≌△CBO(SSS),
∴∠A=∠B,
∵∠A+∠B=180°,
∴∠A=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
23.(1)∵,
∴,,
又∵,
∴,
∴,
∴四边形是平行四边形;
(2)∵平分,
∴,
∵,
∴,
∴,
∴,
又∵,
∴
