2020-2021学年高一数学人教A版必修4第一章1.3 三角函数的诱导公式课件(两课时 共66张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修4第一章1.3 三角函数的诱导公式课件(两课时 共66张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 00:00:00 | ||
图片预览










文档简介
(共66张PPT)
本章内容
1.1
任意角和弧度制
1.2
任意角的三角函数
1.3
三角函数的诱导公式
1.4
三角函数的图象与性质
1.5
函数
y=Asin(wx+j)
的图象
1.6
三角函数模型的简单应用
第一章
小结
1.3
三角函数的诱导公式(第一课时)
1.3
三角函数的诱导公式(第二课时)
(第一课时)
返回目录
1.
sin(2kp+a)=sina
吗?
余弦和正切呢?
2.
sin(kp+a)=sina
吗?
sin(kp-a)=sina
吗?
余弦和正切呢?
3.
诱导公式一是
“2kp+a”
与
“a”
的三角函数关系,
诱导公式二、三、四分别是哪样的关系?
这些关系式是怎样的?
4.
用诱导公式一、二、三、四能解决三角函数中哪样的问题?
问题
1.
前面我们学了一组公式,
只要知道
a
的三角函数值,
就可求得
a
+2kp
的三角函数值.
(1)
你还能写出这组公式吗?
(2)
类似地,
如果知道
a
的三角函数值,
能求出
p
+a,
p
-a
的三角函数值吗?
sin(a+2kp)
=
sina.
cos(a+2kp)
=
cosa.
tan(a+2kp)
=
tana.
诱导公式一:
sin(a+p)
=
sina
成立吗
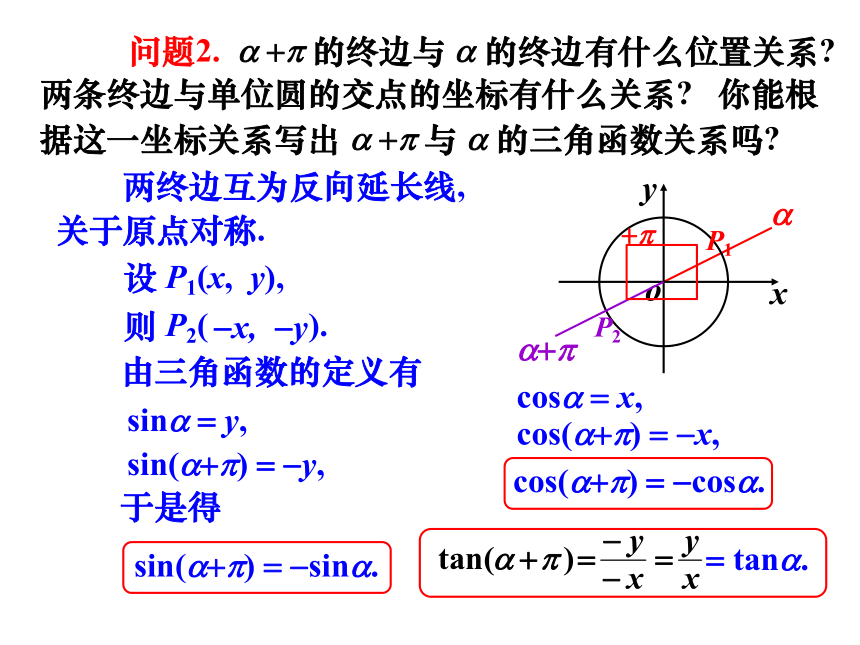
问题2.
a
+p
的终边与
a
的终边有什么位置关系?两条终边与单位圆的交点的坐标有什么关系?
你能根据这一坐标关系写出
a
+p
与
a
的三角函数关系吗?
x
y
o
P1
P2
a
a+p
两终边互为反向延长线,
关于原点对称.
设
P1(x,
y),
则
P2(
).
-x,
-y
由三角函数的定义有
sina
=
y,
sin(a+p)
=
-y,
于是得
sin(a+p)
=
-sina.
cosa
=
x,
cos(a+p)
=
-x,
cos(a+p)
=
-cosa.
=
tana.
+p
同理:
p-a
的终边与
a
的终边关于
y
轴对称,
x
y
o
P1
P2
a
p-a
设
P1(x,
y),
则
P2(
).
-x,
y
sina
=
y,
sin(a+p)
=
y,
得
sin(p-a)
=
sina.
cosa
=
x,
cos(p-a)
=
-x,
得
cos(p-a)
=
-cosa.
得
tan(p-a)
=
-tana.
p
-a
同理:
-a
的终边与
a
的终边关于
x
轴对称,
x
y
o
P1
P2
a
-a
设
P1(x,
y),
则
P2(
).
x,
-y
sina
=
y,
sin(-a)
=
-y,
得
sin(-a)
=
-sina.
cosa
=
x,
cos(-a)
=
x,
得
cos(-a)
=
cosa.
得
tan(-a)
=
-tana.
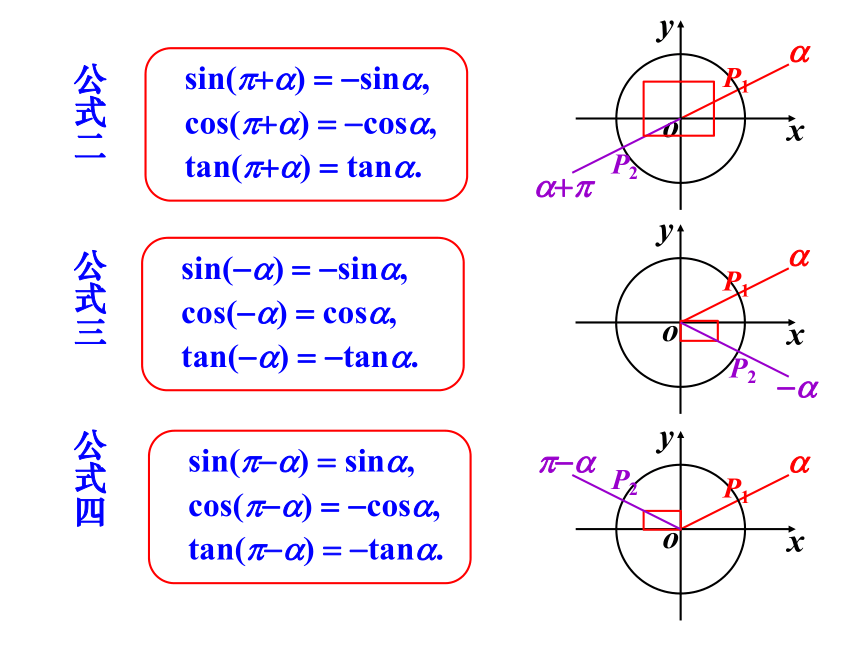
公式二
公式三
公式四
x
y
o
P1
P2
a
a+p
x
y
o
P1
P2
a
p-a
x
y
o
P1
P2
a
-a
sin(p+a)
=
-sina,
cos(p+a)
=
-cosa,
tan(p+a)
=
tana.
sin(p-a)
=
sina,
cos(p-a)
=
-cosa,
tan(p-a)
=
-tana.
sin(-a)
=
-sina,
cos(-a)
=
cosa,
tan(-a)
=
-tana.
利用公式一
~
四,
可把任意角的三角函数转化成0?~90?间的三角函数求值.
负角变正角(公式三),
大角化小角(公式一),
优角用
p
+a
(公式二),
钝角用
p-a
(公式四).
sin(-a)
=
-sina,
cos(-a)
=
cosa,
tan(-a)
=
-tana.
sin(a+2kp)
=
sina.
cos(a+2kp)
=
cosa.
tan(a+2kp)
=
tana.
sin(p+a)
=
-sina,
cos(p+a)
=
-cosa,
tan(p+a)
=
tana.
sin(p-a)
=
sina,
cos(p-a)
=
-cosa,
tan(p-a)
=
-tana.
例
1.
利用公式求下列三角函数值:
(1)
cos225?;
(2)
(3)
(4)
cos(-2040?).
解:
(1)
cos225?=
cos(180?+45?)
=
-cos45?
(优角化锐角)
例
1.
利用公式求下列三角函数值:
(1)
cos225?;
(2)
(3)
(4)
cos(-2040?).
解:
(2)
(大角化小角)
(负角化正角)
例
1.
利用公式求下列三角函数值:
(1)
cos225?;
(2)
(3)
(4)
cos(-2040?).
解:
(3)
(负角化正角)
(大角化小角)
(负角化正角)
(钝角化锐角)
例
1.
利用公式求下列三角函数值:
(1)
cos225?;
(2)
(3)
(4)
cos(-2040?).
解:
(4)
cos(-2040?)
=
cos(2040?)
=
cos(6?360?-120?)
(负角化正角)
(大角化小角)
=
cos(-120?)
=
cos(180?-60?)
(钝角化锐角)
=
-cos60?
=
cos120?
(负角化正角)
例2.
化简
解:
=
1.
原式
=
-cosa
·sina
-sin(a+180?)
·cos(180?+a)
sina
·(-cosa)
-cosa
·sina
=
练习:
(课本27页)
第
1、2、3
题.
1.
将下列三角函数转化为锐角三角函数,
并填在题中横线上:
(1)
cos
=
;
(2)
sin(1+p)
=
;
(3)
sin
=
;
(4)
cos(-70?6
?)
=
.
-sin1
cos70?6?
练习:
(课本27页)
2.
利用公式求下列三角函数值:
(1)
cos(-420?);
(2)
(3)
sin(-1300?);
(4)
解:
(1)
cos(-420?)
=
cos420?
=
cos(360?+60?)
=
cos60?
(2)
2.
利用公式求下列三角函数值:
(1)
cos(-420?);
(2)
(3)
sin(-1300?);
(4)
解:
(3)
sin(-1300?)
=
-sin1300?
=
-sin(3?360?+220?)
=
-sin220?
=
-sin(180?+40?)
=
sin40?
≈0.6428.
2.
利用公式求下列三角函数值:
(1)
cos(-420?);
(2)
(3)
sin(-1300?);
(4)
解:
(4)
3.
化简:
(1)
sin(a+180)cos(-a)sin(-a-180);
(2)
sin3(-a)cos(2p+a)tan(-a-p).
解:
(1)
原式
=
-sina
cosa
[-sin(a+180?)]
=
-sina
cosa
sina
=
-sin2a
cosa
.
(2)
原式
=
-sin3a
cosa
[-tan(a+p)]
=
-sin3a
cosa
(-tana)
=
sin4a.
【课时小结】
诱导公式以及应用要点
sin(-a)
=
-sina,
cos(-a)
=
cosa,
tan(-a)
=
-tana.
sin(a+2kp)
=
sina.
cos(a+2kp)
=
cosa.
tan(a+2kp)
=
tana.
sin(p+a)
=
-sina,
cos(p+a)
=
-cosa,
tan(p+a)
=
tana.
sin(p-a)
=
sina,
cos(p-a)
=
-cosa,
tan(p-a)
=
-tana.
公式一
公式二
公式三
公式四
大角变小角
负角变正角
优角变小角
钝角变锐角
习题
1.3
A
组
第
1、2
题.
习题
1.3
A
组
1.
将下列三角函数转化为锐角三角函数,
并填在题中横线上:
(1)
cos210?
=
;
(2)
sin263?42?
=
;
(3)
(4)
(5)
(6)
cos(-104?26?)
=
;
(7)
tan632?24?
=
;
(8)
-cos30?
-sin83?42?
-cos75?34?
-tan87?36?
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(1)
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(2)
sin(-1574?)
=
-sin1574?
=
-sin(4?360?+134?)
=
-sin134?
=
-sin(180?-46?)
=
-sin46?
≈-0.7193.
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(3)
sin(-2160?52?)
=
-sin2160?52?
=
-sin(6?360?+52?)
=
-sin52?
≈-0.0151.
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(4)
cos(-1751?36?)
=
cos1751?36?
=
cos(4?360?+311?36?)
=
cos311?36?
=
cos(360?-48?24?)
=
cos(-48?24?)
≈0.6639.
=
cos48?24?
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(5)
cos1615?8?
=
cos(4?360?+175?8?)
=
cos175?8?
=
cos(180?-4?52?)
=
-cos4?52?
≈-0.9964.
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(6)
(第二课时)
返回目录
2.
有多少个诱导公式,
这些公式各有什么作用?你用什么方法能较好地把它们熟记?
1.
的三角函数有什么关系?
与
a
呢?
复习:
请同学们写出四组诱导公式.
公式二
公式三
公式四
sin(p+a)
=
-sina,
cos(p+a)
=
-cosa,
tan(p+a)
=
tana.
sin(p-a)
=
sina,
cos(p-a)
=
-cosa,
tan(p-a)
=
-tana.
sin(-a)
=
-sina,
cos(-a)
=
cosa,
tan(-a)
=
-tana.
sin(a+2kp)=sina,
cos(a+2kp)=cosa,
tan(a+2kp)=tana.
公式一
4.
填表:
a
tana
cosa
sina
x
y
o
-1
1
1
法一,
用诱导公式计算.
法二,
看角的终边位置确定.
练习:
(课本28页)
(请同学们填在你的课本上)
x
y
o
P
a
【诱导公式五、六】
(互余函数公式)
问题
3.
±a
的终边与
a
的终边的位置关系关
于什么对称?
两条终边与单位圆的交点的坐标是什么
样的关系?
你能根据这一坐标关系写出
±a
与
a
的三角函数的关系吗?
P1
P2
-a
a
设
P(x,
y),
则
P1(y,
x),
P2(-y,
x).
sina
=
y,
cosa
=
x,
公式五
公式六
例3.
证明:
(1)
(2)
证明:
(1)
=
-cosa.
(2)
=
-sina.
证明:
(1)
(2)
证明:
(1)
=
-cosa.
(2)
=
sina.
练习:
(补充)
sin(-a)
=
-sina,
cos(-a)
=
cosa,
tan(-a)
=
-tana.
sin(a+2kp)
=
sina.
cos(a+2kp)
=
cosa.
tan(a+2kp)
=
tana.
sin(p+a)
=
-sina,
cos(p+a)
=
-cosa,
tan(p+a)
=
tana.
sin(p-a)
=
sina,
cos(p-a)
=
-cosa,
tan(p-a)
=
-tana.
为了便于记忆,
在各组公式中,
我们把
a
看作锐角,
则如图:
x
y
O
2kp+a
p+a
p-a
-a
一
象限
三象限
四
象限
二
象限
横轴加减,
同名函数,
象限位置定正负.
为了便于记忆,
在各组公式中,
我们把
a
看作锐角,
则如图:
x
y
O
一
象限
二象限
三
象限
四
象限
纵轴加减,
互余函数,
象限位置定正负.
例
4.
化简
解:
原式
=
sin(-a)
(-cosa)
(-sina)
(-cosa)
sina
[-sin(p+a)]
-cosa
sin2a
-cosa
sin2a
=
=
-tana.
练习:
(补充)
1.
将下列各函数化成锐角的互余函数:
(1)
sin195?;
(2)
cos(-130?);
(3)
2.
化简下列各式:
(1)
(2)
1.
将下列各函数化成锐角的互余函数:
(1)
sin195?;
(2)
cos(-130?);
(3)
解:
(1)
sin195?=
sin(
270?-75?)
=
-cos75?.
(2)
cos(-130?)
=
cos(
-90?-40?)
=
-sin40?.
(3)
解:
(1)
原式
=
-tana
·sina
·(-cosa)
+(-cosa)2
=
sin2a
+cos2a
=1.
2.
化简下列各式:
(1)
(2)
解:
(2)
原式
=
=
-1.
2.
化简下列各式:
(1)
(2)
(
解题思想:
变为同角,
向20?靠近
)
sin20?-cos20?的正负?
(三角函数线)
【课时小结】
1.
诱导公式五、六
(互余函数公式)
公式五
公式六
补充公式:
【课时小结】
2.
公式的记忆
x
y
O
2kp+a
p+a
p-a
-a
横轴加减,
同名函数,
象限位置定正负.
同名函数公式
纵轴加减,
互余函数,
象限位置定正负.
x
y
O
互余函数公式
【课时小结】
3.
公式应用
x
y
O
2kp+a
p+a
p-a
-a
x
y
O
负角化正角:
(-a)
大角化小角:
(2kp+a)
优角化小角:
(p+a)
钝角化锐角:
(p-a)
一象限角化互余
二象限角化互余
三象限角化互余
四象限角化互余
练习:
(课本28页)
第
5、6、7
题.
习题
1.3
A
组
第
3、4
题.
B
组
第
1、2
题.
5.
将下列三角函数转化为锐角三角函数,
并填在题中的横线上:
(1)
tan
=
;
(2)
tan100?21?=
;
(3)
tan
=
;
(4)
tan324?32?=
.
解:
(1)
(2)
tan100?21?
=
tan(180?-79?39?)
=
-tan79?39?.
-tan79?39?
(3)
(4)
tan324?32?
=
tan(360?-35?28?)
=
tan(-35?28?)
=
-tan35?28?.
-tan35?28?
练习:
(课本28页)
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(1)
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(2)
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(3)
cos(-1182?13?)
=
cos1182?13?
=
cos(3?360?+102?13?)
=
cos102?13?
=
cos(180?-77?47?)
=
-cos77?47?
≈-0.2116.
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(4)
sin670?39?)
=
sin(720?-49?21?)
=
sin(-49?21?)
=
-sin49?21?
≈-0.7587.
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(5)
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(6)
tan580?21?
=
tan(360?+220?21?)
=
tan220?21?
=
tan(180?+40?21?)
=
tan40?21?
≈0.8496.
7.
化简:
(1)
(2)
解:
(1)
原式
=
·sina·cos(-a)
·sina·cosa
=
sin2a.
7.
化简:
(1)
(2)
解:
(2)
原式
=
cos2a
-
3.
化简:
(1)
sin(-1071?)·sin99?+sin(-171?)·sin(-261?);
(2)
1+sin(a-2p)·sin(p+a)-2cos2(-a).
解:
(1)
原式
=
-sin1071?sin99?+sin171?sin261?
=
-sin(3?360?-9?)sin(90?+9?)
+sin(180?-9?)sin(180?+81?)
=
sin9?cos9?+sin9?(-sin81?)
=
sin9?cos9?-sin9?sin(90?-9?)
=
sin9?cos9?-sin9?cos9?
=
0.
习题
1.3
A
组
3.
化简:
(1)
sin(-1071?)·sin99?+sin(-171?)·sin(-261?);
(2)
1+sin(a-2p)·sin(p+a)-2cos2(-a).
解:
(2)
原式
=
1+sina(-sina)-2cos2a
=
1-sin2a-2cos2a
=
1-(sin2a+cos2a)-
cos2a
=
1-1-
cos2a
=
-
cos2a.
习题
1.3
A
组
4.
求证:
(1)
sin(360?-
a)
=
-sina;
(2)
cos(360?-
a)
=
cosa;
(3)
tan(360?-
a)
=
-tana.
(此组结论与诱导公式中
-a
那一组相同,
记住有用)
证明:
(1)
sin(360?-a)
=
sin(-a)
=
-sina.
(2)
cos(360?-a)
=
cos(-a)
=
cosa.
(3)
tan(360?-a)
=
tan(-a)
=
-tana.
B
组
1.
计算:
(1)
sin420?·cos750?+sin(-330?)·cos(-660?);
(2)
tan675?+tan765?-tan(-330?)+tan(-690?);
(3)
解:
(1)
原式
=
sin(360?+60?)cos(720?+30?)-sin330?cos660?
=
sin60?cos30?-sin(360?-30?)cos(720?-60?)
=
sin60?cos30?-sin(-30?)cos(-60?)
=
sin60?cos30?+sin30?cos60?
=1.
B
组
1.
计算:
(1)
sin420?·cos750?+sin(-330?)·cos(-660?);
(2)
tan675?+tan765?-tan(-330?)+tan(-690?);
(3)
解:
(2)
原式
=
tan(720?-45?)+tan(720?+45?)+tan330?
-
tan690?
=
tan(-45?)+tan45?+tan(360?-30?)
=
-tan45?+tan45?+tan(-30?)-tan(-30?)
=
0.
-
tan(720?-30?)
B
组
1.
计算:
(1)
sin420?·cos750?+sin(-330?)·cos(-660?);
(2)
tan675?+tan765?-tan(-330?)+tan(-690?);
(3)
解:
(3)
原式
=
=
0.
2.
已知
sin(p+a)
=
计算:
(1)
sin(5p-a);
(2)
(3)
(4)
解:
(1)
sin(5p-a)
=
sina
(2)
(3)
=
-sina
(4)
本章内容
1.1
任意角和弧度制
1.2
任意角的三角函数
1.3
三角函数的诱导公式
1.4
三角函数的图象与性质
1.5
函数
y=Asin(wx+j)
的图象
1.6
三角函数模型的简单应用
第一章
小结
1.3
三角函数的诱导公式(第一课时)
1.3
三角函数的诱导公式(第二课时)
(第一课时)
返回目录
1.
sin(2kp+a)=sina
吗?
余弦和正切呢?
2.
sin(kp+a)=sina
吗?
sin(kp-a)=sina
吗?
余弦和正切呢?
3.
诱导公式一是
“2kp+a”
与
“a”
的三角函数关系,
诱导公式二、三、四分别是哪样的关系?
这些关系式是怎样的?
4.
用诱导公式一、二、三、四能解决三角函数中哪样的问题?
问题
1.
前面我们学了一组公式,
只要知道
a
的三角函数值,
就可求得
a
+2kp
的三角函数值.
(1)
你还能写出这组公式吗?
(2)
类似地,
如果知道
a
的三角函数值,
能求出
p
+a,
p
-a
的三角函数值吗?
sin(a+2kp)
=
sina.
cos(a+2kp)
=
cosa.
tan(a+2kp)
=
tana.
诱导公式一:
sin(a+p)
=
sina
成立吗
问题2.
a
+p
的终边与
a
的终边有什么位置关系?两条终边与单位圆的交点的坐标有什么关系?
你能根据这一坐标关系写出
a
+p
与
a
的三角函数关系吗?
x
y
o
P1
P2
a
a+p
两终边互为反向延长线,
关于原点对称.
设
P1(x,
y),
则
P2(
).
-x,
-y
由三角函数的定义有
sina
=
y,
sin(a+p)
=
-y,
于是得
sin(a+p)
=
-sina.
cosa
=
x,
cos(a+p)
=
-x,
cos(a+p)
=
-cosa.
=
tana.
+p
同理:
p-a
的终边与
a
的终边关于
y
轴对称,
x
y
o
P1
P2
a
p-a
设
P1(x,
y),
则
P2(
).
-x,
y
sina
=
y,
sin(a+p)
=
y,
得
sin(p-a)
=
sina.
cosa
=
x,
cos(p-a)
=
-x,
得
cos(p-a)
=
-cosa.
得
tan(p-a)
=
-tana.
p
-a
同理:
-a
的终边与
a
的终边关于
x
轴对称,
x
y
o
P1
P2
a
-a
设
P1(x,
y),
则
P2(
).
x,
-y
sina
=
y,
sin(-a)
=
-y,
得
sin(-a)
=
-sina.
cosa
=
x,
cos(-a)
=
x,
得
cos(-a)
=
cosa.
得
tan(-a)
=
-tana.
公式二
公式三
公式四
x
y
o
P1
P2
a
a+p
x
y
o
P1
P2
a
p-a
x
y
o
P1
P2
a
-a
sin(p+a)
=
-sina,
cos(p+a)
=
-cosa,
tan(p+a)
=
tana.
sin(p-a)
=
sina,
cos(p-a)
=
-cosa,
tan(p-a)
=
-tana.
sin(-a)
=
-sina,
cos(-a)
=
cosa,
tan(-a)
=
-tana.
利用公式一
~
四,
可把任意角的三角函数转化成0?~90?间的三角函数求值.
负角变正角(公式三),
大角化小角(公式一),
优角用
p
+a
(公式二),
钝角用
p-a
(公式四).
sin(-a)
=
-sina,
cos(-a)
=
cosa,
tan(-a)
=
-tana.
sin(a+2kp)
=
sina.
cos(a+2kp)
=
cosa.
tan(a+2kp)
=
tana.
sin(p+a)
=
-sina,
cos(p+a)
=
-cosa,
tan(p+a)
=
tana.
sin(p-a)
=
sina,
cos(p-a)
=
-cosa,
tan(p-a)
=
-tana.
例
1.
利用公式求下列三角函数值:
(1)
cos225?;
(2)
(3)
(4)
cos(-2040?).
解:
(1)
cos225?=
cos(180?+45?)
=
-cos45?
(优角化锐角)
例
1.
利用公式求下列三角函数值:
(1)
cos225?;
(2)
(3)
(4)
cos(-2040?).
解:
(2)
(大角化小角)
(负角化正角)
例
1.
利用公式求下列三角函数值:
(1)
cos225?;
(2)
(3)
(4)
cos(-2040?).
解:
(3)
(负角化正角)
(大角化小角)
(负角化正角)
(钝角化锐角)
例
1.
利用公式求下列三角函数值:
(1)
cos225?;
(2)
(3)
(4)
cos(-2040?).
解:
(4)
cos(-2040?)
=
cos(2040?)
=
cos(6?360?-120?)
(负角化正角)
(大角化小角)
=
cos(-120?)
=
cos(180?-60?)
(钝角化锐角)
=
-cos60?
=
cos120?
(负角化正角)
例2.
化简
解:
=
1.
原式
=
-cosa
·sina
-sin(a+180?)
·cos(180?+a)
sina
·(-cosa)
-cosa
·sina
=
练习:
(课本27页)
第
1、2、3
题.
1.
将下列三角函数转化为锐角三角函数,
并填在题中横线上:
(1)
cos
=
;
(2)
sin(1+p)
=
;
(3)
sin
=
;
(4)
cos(-70?6
?)
=
.
-sin1
cos70?6?
练习:
(课本27页)
2.
利用公式求下列三角函数值:
(1)
cos(-420?);
(2)
(3)
sin(-1300?);
(4)
解:
(1)
cos(-420?)
=
cos420?
=
cos(360?+60?)
=
cos60?
(2)
2.
利用公式求下列三角函数值:
(1)
cos(-420?);
(2)
(3)
sin(-1300?);
(4)
解:
(3)
sin(-1300?)
=
-sin1300?
=
-sin(3?360?+220?)
=
-sin220?
=
-sin(180?+40?)
=
sin40?
≈0.6428.
2.
利用公式求下列三角函数值:
(1)
cos(-420?);
(2)
(3)
sin(-1300?);
(4)
解:
(4)
3.
化简:
(1)
sin(a+180)cos(-a)sin(-a-180);
(2)
sin3(-a)cos(2p+a)tan(-a-p).
解:
(1)
原式
=
-sina
cosa
[-sin(a+180?)]
=
-sina
cosa
sina
=
-sin2a
cosa
.
(2)
原式
=
-sin3a
cosa
[-tan(a+p)]
=
-sin3a
cosa
(-tana)
=
sin4a.
【课时小结】
诱导公式以及应用要点
sin(-a)
=
-sina,
cos(-a)
=
cosa,
tan(-a)
=
-tana.
sin(a+2kp)
=
sina.
cos(a+2kp)
=
cosa.
tan(a+2kp)
=
tana.
sin(p+a)
=
-sina,
cos(p+a)
=
-cosa,
tan(p+a)
=
tana.
sin(p-a)
=
sina,
cos(p-a)
=
-cosa,
tan(p-a)
=
-tana.
公式一
公式二
公式三
公式四
大角变小角
负角变正角
优角变小角
钝角变锐角
习题
1.3
A
组
第
1、2
题.
习题
1.3
A
组
1.
将下列三角函数转化为锐角三角函数,
并填在题中横线上:
(1)
cos210?
=
;
(2)
sin263?42?
=
;
(3)
(4)
(5)
(6)
cos(-104?26?)
=
;
(7)
tan632?24?
=
;
(8)
-cos30?
-sin83?42?
-cos75?34?
-tan87?36?
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(1)
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(2)
sin(-1574?)
=
-sin1574?
=
-sin(4?360?+134?)
=
-sin134?
=
-sin(180?-46?)
=
-sin46?
≈-0.7193.
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(3)
sin(-2160?52?)
=
-sin2160?52?
=
-sin(6?360?+52?)
=
-sin52?
≈-0.0151.
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(4)
cos(-1751?36?)
=
cos1751?36?
=
cos(4?360?+311?36?)
=
cos311?36?
=
cos(360?-48?24?)
=
cos(-48?24?)
≈0.6639.
=
cos48?24?
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(5)
cos1615?8?
=
cos(4?360?+175?8?)
=
cos175?8?
=
cos(180?-4?52?)
=
-cos4?52?
≈-0.9964.
2.
用诱导公式求下列三角函数值:
(1)
(2)
sin(-1574?);
(3)
sin(-2160?52?);
(4)
cos(-1751?36?);
(5)
cos1615?8?;
(6)
解:
(6)
(第二课时)
返回目录
2.
有多少个诱导公式,
这些公式各有什么作用?你用什么方法能较好地把它们熟记?
1.
的三角函数有什么关系?
与
a
呢?
复习:
请同学们写出四组诱导公式.
公式二
公式三
公式四
sin(p+a)
=
-sina,
cos(p+a)
=
-cosa,
tan(p+a)
=
tana.
sin(p-a)
=
sina,
cos(p-a)
=
-cosa,
tan(p-a)
=
-tana.
sin(-a)
=
-sina,
cos(-a)
=
cosa,
tan(-a)
=
-tana.
sin(a+2kp)=sina,
cos(a+2kp)=cosa,
tan(a+2kp)=tana.
公式一
4.
填表:
a
tana
cosa
sina
x
y
o
-1
1
1
法一,
用诱导公式计算.
法二,
看角的终边位置确定.
练习:
(课本28页)
(请同学们填在你的课本上)
x
y
o
P
a
【诱导公式五、六】
(互余函数公式)
问题
3.
±a
的终边与
a
的终边的位置关系关
于什么对称?
两条终边与单位圆的交点的坐标是什么
样的关系?
你能根据这一坐标关系写出
±a
与
a
的三角函数的关系吗?
P1
P2
-a
a
设
P(x,
y),
则
P1(y,
x),
P2(-y,
x).
sina
=
y,
cosa
=
x,
公式五
公式六
例3.
证明:
(1)
(2)
证明:
(1)
=
-cosa.
(2)
=
-sina.
证明:
(1)
(2)
证明:
(1)
=
-cosa.
(2)
=
sina.
练习:
(补充)
sin(-a)
=
-sina,
cos(-a)
=
cosa,
tan(-a)
=
-tana.
sin(a+2kp)
=
sina.
cos(a+2kp)
=
cosa.
tan(a+2kp)
=
tana.
sin(p+a)
=
-sina,
cos(p+a)
=
-cosa,
tan(p+a)
=
tana.
sin(p-a)
=
sina,
cos(p-a)
=
-cosa,
tan(p-a)
=
-tana.
为了便于记忆,
在各组公式中,
我们把
a
看作锐角,
则如图:
x
y
O
2kp+a
p+a
p-a
-a
一
象限
三象限
四
象限
二
象限
横轴加减,
同名函数,
象限位置定正负.
为了便于记忆,
在各组公式中,
我们把
a
看作锐角,
则如图:
x
y
O
一
象限
二象限
三
象限
四
象限
纵轴加减,
互余函数,
象限位置定正负.
例
4.
化简
解:
原式
=
sin(-a)
(-cosa)
(-sina)
(-cosa)
sina
[-sin(p+a)]
-cosa
sin2a
-cosa
sin2a
=
=
-tana.
练习:
(补充)
1.
将下列各函数化成锐角的互余函数:
(1)
sin195?;
(2)
cos(-130?);
(3)
2.
化简下列各式:
(1)
(2)
1.
将下列各函数化成锐角的互余函数:
(1)
sin195?;
(2)
cos(-130?);
(3)
解:
(1)
sin195?=
sin(
270?-75?)
=
-cos75?.
(2)
cos(-130?)
=
cos(
-90?-40?)
=
-sin40?.
(3)
解:
(1)
原式
=
-tana
·sina
·(-cosa)
+(-cosa)2
=
sin2a
+cos2a
=1.
2.
化简下列各式:
(1)
(2)
解:
(2)
原式
=
=
-1.
2.
化简下列各式:
(1)
(2)
(
解题思想:
变为同角,
向20?靠近
)
sin20?-cos20?的正负?
(三角函数线)
【课时小结】
1.
诱导公式五、六
(互余函数公式)
公式五
公式六
补充公式:
【课时小结】
2.
公式的记忆
x
y
O
2kp+a
p+a
p-a
-a
横轴加减,
同名函数,
象限位置定正负.
同名函数公式
纵轴加减,
互余函数,
象限位置定正负.
x
y
O
互余函数公式
【课时小结】
3.
公式应用
x
y
O
2kp+a
p+a
p-a
-a
x
y
O
负角化正角:
(-a)
大角化小角:
(2kp+a)
优角化小角:
(p+a)
钝角化锐角:
(p-a)
一象限角化互余
二象限角化互余
三象限角化互余
四象限角化互余
练习:
(课本28页)
第
5、6、7
题.
习题
1.3
A
组
第
3、4
题.
B
组
第
1、2
题.
5.
将下列三角函数转化为锐角三角函数,
并填在题中的横线上:
(1)
tan
=
;
(2)
tan100?21?=
;
(3)
tan
=
;
(4)
tan324?32?=
.
解:
(1)
(2)
tan100?21?
=
tan(180?-79?39?)
=
-tan79?39?.
-tan79?39?
(3)
(4)
tan324?32?
=
tan(360?-35?28?)
=
tan(-35?28?)
=
-tan35?28?.
-tan35?28?
练习:
(课本28页)
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(1)
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(2)
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(3)
cos(-1182?13?)
=
cos1182?13?
=
cos(3?360?+102?13?)
=
cos102?13?
=
cos(180?-77?47?)
=
-cos77?47?
≈-0.2116.
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(4)
sin670?39?)
=
sin(720?-49?21?)
=
sin(-49?21?)
=
-sin49?21?
≈-0.7587.
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(5)
6.
用诱导公式求下列三角函数值
(可用计算器):
(1)
(2)
(3)
cos(-1182?13?);
(4)
sin670?39?;
(5)
(6)
tan580?21?.
解:
(6)
tan580?21?
=
tan(360?+220?21?)
=
tan220?21?
=
tan(180?+40?21?)
=
tan40?21?
≈0.8496.
7.
化简:
(1)
(2)
解:
(1)
原式
=
·sina·cos(-a)
·sina·cosa
=
sin2a.
7.
化简:
(1)
(2)
解:
(2)
原式
=
cos2a
-
3.
化简:
(1)
sin(-1071?)·sin99?+sin(-171?)·sin(-261?);
(2)
1+sin(a-2p)·sin(p+a)-2cos2(-a).
解:
(1)
原式
=
-sin1071?sin99?+sin171?sin261?
=
-sin(3?360?-9?)sin(90?+9?)
+sin(180?-9?)sin(180?+81?)
=
sin9?cos9?+sin9?(-sin81?)
=
sin9?cos9?-sin9?sin(90?-9?)
=
sin9?cos9?-sin9?cos9?
=
0.
习题
1.3
A
组
3.
化简:
(1)
sin(-1071?)·sin99?+sin(-171?)·sin(-261?);
(2)
1+sin(a-2p)·sin(p+a)-2cos2(-a).
解:
(2)
原式
=
1+sina(-sina)-2cos2a
=
1-sin2a-2cos2a
=
1-(sin2a+cos2a)-
cos2a
=
1-1-
cos2a
=
-
cos2a.
习题
1.3
A
组
4.
求证:
(1)
sin(360?-
a)
=
-sina;
(2)
cos(360?-
a)
=
cosa;
(3)
tan(360?-
a)
=
-tana.
(此组结论与诱导公式中
-a
那一组相同,
记住有用)
证明:
(1)
sin(360?-a)
=
sin(-a)
=
-sina.
(2)
cos(360?-a)
=
cos(-a)
=
cosa.
(3)
tan(360?-a)
=
tan(-a)
=
-tana.
B
组
1.
计算:
(1)
sin420?·cos750?+sin(-330?)·cos(-660?);
(2)
tan675?+tan765?-tan(-330?)+tan(-690?);
(3)
解:
(1)
原式
=
sin(360?+60?)cos(720?+30?)-sin330?cos660?
=
sin60?cos30?-sin(360?-30?)cos(720?-60?)
=
sin60?cos30?-sin(-30?)cos(-60?)
=
sin60?cos30?+sin30?cos60?
=1.
B
组
1.
计算:
(1)
sin420?·cos750?+sin(-330?)·cos(-660?);
(2)
tan675?+tan765?-tan(-330?)+tan(-690?);
(3)
解:
(2)
原式
=
tan(720?-45?)+tan(720?+45?)+tan330?
-
tan690?
=
tan(-45?)+tan45?+tan(360?-30?)
=
-tan45?+tan45?+tan(-30?)-tan(-30?)
=
0.
-
tan(720?-30?)
B
组
1.
计算:
(1)
sin420?·cos750?+sin(-330?)·cos(-660?);
(2)
tan675?+tan765?-tan(-330?)+tan(-690?);
(3)
解:
(3)
原式
=
=
0.
2.
已知
sin(p+a)
=
计算:
(1)
sin(5p-a);
(2)
(3)
(4)
解:
(1)
sin(5p-a)
=
sina
(2)
(3)
=
-sina
(4)
