2020-2021学年高一数学人教A版必修4第一章1.5 函数y=Asin(wx+j)的图象2课时课件( 共63张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修4第一章1.5 函数y=Asin(wx+j)的图象2课时课件( 共63张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 17:16:22 | ||
图片预览











文档简介
(共63张PPT)
本章内容
1.1
任意角和弧度制
1.2
任意角的三角函数
1.3
三角函数的诱导公式
1.4
三角函数的图象与性质
1.5
函数
y=Asin(wx+j)
的图象
1.6
三角函数模型的简单应用
第一章
小结
函数
y=Asin(wx+j)
的图象
第一课时
第二课时
(第一课时)
返回目录
2.
函数
y=Asin(wx+j)
的图象可由正弦曲线
y=sinx
怎么变化得来?
1.
函数
y=sin3x
的图象可由
y=sinx
的图象怎样变化得来?
与
y=3sinx
的图象呢?
1.
y=sinx
与
y=sin(x+j)
画出
y
=
sinx
与
y
=
sin(x+
)
的图象.
x
y
o
2p
p
y=sinx
的图象完全一样,
只是
位置不同.
可看出
的图象可由
y
=
sinx
的图象向左平移
个单位得到.
再设
画
的图象.
的图象可由
y
=
sinx
的图象向右
平移
个单位得到.
设
j
=
一般地,
函数
y
=
sin(x+j),
x?R
(其中j
?
0)
的图象,
可以看作把正弦曲线上所有的点向左
(当j>0时)
或向右
(当j<0时)
平行移动
|
j
|
个单位长度而得到.
(初始位置变化)
左右平移
结论:
左
加
右
减
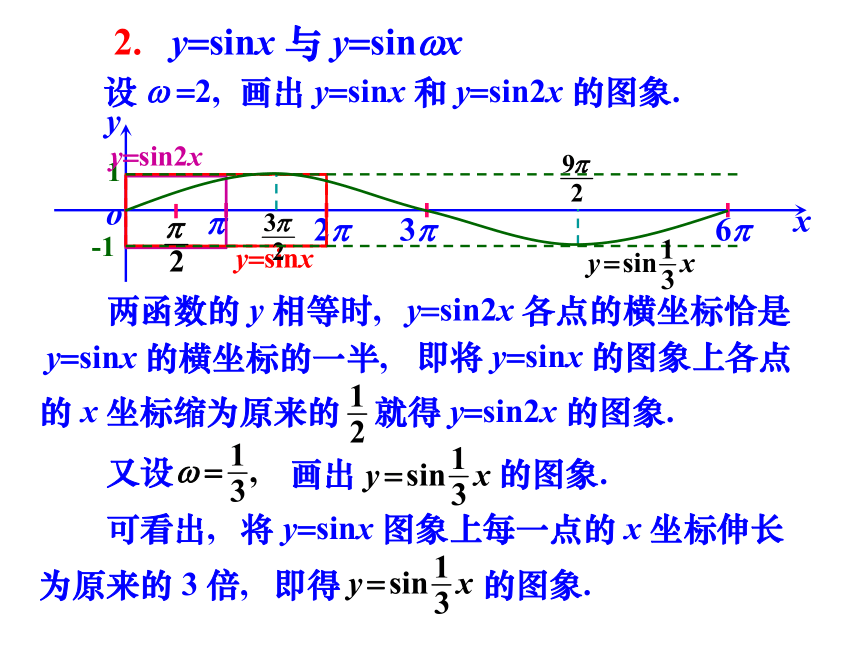
2.
y=sinx
与
y=sinwx
设
w
=2,
画出
y=sinx
和
y=sin2x
的图象.
1
x
y
o
6p
3p
2p
p
y=sinx
y=sin2x
-1
两函数的
y
相等时,
y=sin2x
各点的横坐标恰是
y=sinx
的横坐标的一半,
即将
y=sinx
的图象上各点
的
x
坐标缩为原来的
就得
y=sin2x
的图象.
又设
画出
的图象.
可看出,
将
y=sinx
图象上每一点的
x
坐标伸长
为原来的
3
倍,
即得
的图象.
一般地,
函数
y
=
sinwx,
x?R
(其中w
>0且w≠1)
的图象,
可以看作把正弦曲线上所有点的横坐标缩短
(当w
>1时)
或伸长
(当0到原来的
倍
(
纵坐
标不变
)
而得到.
(周期变化)
结论:
x
坐标的伸缩
w
>1,
缩短,
w
<1,
伸长,
3.
y=sinx
与
y=Asinx
设
A
=2,
画出
y=sinx
和
y=2sinx
的图象.
x
y
o
y=sinx
y=2sinx
2
-2
1
-1
p
2p
在
x
坐标相同的情况下,
y=2sinx
图象上各点的
y
坐标
是
y=sinx
的
2
倍.
将
y=sinx
的图象沿
y
轴
方向伸长到原来的
2
倍即得
y=2sinx的图象.
又设
画函数
的图象.
将
y=sinx
的图象沿
y
轴方向缩短为原来的
便得到
的图象.
一般地,
函数
y=Asinx
,
x?R
(其中A>0,
且A≠1)
的图象,
可以看作把正弦曲线上所有点的纵坐标伸长
(
当
A>1
时
)
或缩短
(当
0到原来的
A
倍
(横坐标不变)
而得到.
函数
y=Asinx,
x?R的值域是
[
-A,
A
],
最大值是A,
最小值是
-A.
(值域变化)
结论:
y
坐标的伸缩
A
>1,
伸长,
A
<1,
缩短.
综合结论:
一般地,
函数
y=Asin(wx+j),
x?R
(其中A>0,
w>0)的图象,
可以看作用下面的方法得到:
先把正弦曲线上所有的点向左
(当
j>0
时)
或向右
(
当j<0
时
)
平行移动
|
j
|
个单位长度,
再把所得各点的横坐标缩短
(当
w>1
时)
或伸长
(当0到原来的
倍
(纵坐标不变),
再把所得各点的纵坐标伸长
(当
A>1时)
或缩短
(当0到原来的A倍
(横坐标不变).
例
1.
画出函数
的简图.
画法:
1.
画出
y
=
sinx
的简图;
2.
将
y
=
sinx
的图象向右平移
个单位得到
p
2p
1
-1
y
O
x
例
1.
画出函数
的简图.
画法:
1.
画出
y
=
sinx
的简图;
y
O
p
2p
1
-1
x
p
标伸长为原来的
3
倍,
得到
3.
又将
的图象的
y
坐标不变,
x
坐
例
1.
画出函数
的简图.
画法:
1.
画出
y
=
sinx
的简图;
x
y
O
p
2p
1
-1
标伸长为原来的
3
倍,
得到
3.
又将
的图象的
y
坐标不变,
x
坐
5p
例
1.
画出函数
的简图.
画法:
1.
画出
y
=
sinx
的简图;
x
y
O
p
2p
1
-1
5p
4.
再将
的图象的
x
坐标不变,
y
坐
标伸长为原来的
2
倍,
得到
2
-2
变化顺序:
平移,
x
伸缩,
y
伸缩.
练习:
(课本55页)
第
1、2
题.
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
(1)
x
y
O
p
2p
练习:
(课本55页)
将
y=sinx
的图象上各点
的
y
坐标压缩为原来的一半
即得
的图象.
1
-1
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
五点法:
(1)
x
y
0
p
2p
0
0
0
x
y
O
p
2p
练习:
(课本55页)
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
(2)
x
y
O
练习:
(课本55页)
将
y=sinx
的图象上各点
即得
y=sin3x
的图象.
的
x
坐标压缩为原来的
p
2p
1
-1
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
(3)
x
y
O
1
-1
练习:
(课本55页)
将
y=sinx
的图象向右
平移
个单位即得
的图象.
p
2p
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
(4)
x
y
O
练习:
(课本55页)
将
y=sinx
的图象向右
平移
个单位,
再将各点
的
x
坐标压缩为原来的
再将各点的
y
坐标伸长为
原来的
2
倍即得.
p
2p
1
-1
2
-2
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
五点法:
(4)
y
0
p
2p
0
0
0
x
y
O
x
2
-2
2
-2
练习:
(课本55页)
2.
选择题:
已知函数
的图象为C.
(1)
为了得到函数
的图象,
只要把
C
上所有的点(
).
(A)
向右平行移动
个单位长度.
(B)
向左平行移动
个单位长度.
(C)
向右平行移动
个单位长度.
(D)
向左平行移动
个单位长度.
左加右减,
C
向右移
2.
选择题:
已知函数
的图象为C.
(2)
为了得到函数
的图象,
只要把
C
上所有的点(
).
(A)
横坐标伸长到原来的
2
倍,
纵坐标不变.
(B)
横坐标缩短到原来的
倍,
纵坐标不变.
(C)
纵坐标伸长到原来的
2
倍,
横坐标不变.
(D)
纵坐标缩短到原来的
倍,
横坐标不变.
w>1,
横坐标缩短,
w<1,
横坐标伸长.
B
2.
选择题:
已知函数
的图象为C.
(3)
为了得到函数
的图象,
只要把
C
上所有的点(
).
(A)
横坐标伸长到原来的
倍,
纵坐标不变.
(B)
横坐标缩短到原来的
倍,
纵坐标不变.
(C)
纵坐标伸长到原来的
倍,
横坐标不变.
(D)
纵坐标缩短到原来的
倍,
横坐标不变.
A>1,
纵坐标伸长,
A<1,
纵坐标缩短.
4>3,
伸长
C
【课时小结】
函数
y
=
sin(x+j)
的图象,
可由正弦曲线
y=sinx
的图象向左
(j>0)
或向右
(j<0)
平行移动
|j|
个单位长度而得到.
左
加
右
减
1.
平移
【课时小结】
2.
横向伸缩
函数
y
=
sinwx
(w
>0)
的图象,
可由正弦曲线y=sinx
上所有点的横坐标缩短
(w
>1)
或伸长
(w<1)
到原来的
倍
(
纵坐标不变
)
而得到.
(周期变化)
【课时小结】
3.
纵向伸缩
函数
y
=
Asinx
(A
>0)
的图象,
可由正弦曲线y=sinx
上所有点的纵坐标伸长(A
>1)
或缩短(A<1)
到原来的
A
倍
(
横坐标不变
)
而得到.
【课时小结】
4.
y=Asin(wx+j)
的图象
函数
y=Asin(wx+j)
(A>0,
w>0)的图象,
可用下面的方法得到:
先把正弦曲线上所有的点横向(左加右减)平行移动
|
j
|
个单位长度,
再把所得各点的横坐标伸
缩到原来的
倍
(纵坐标不变),
再把所得各点的纵坐
标伸缩到原来的A倍
(横坐标不变).
习题
1.5
A
组
第
1、2
题.
习题
1.5
A
组
1.
选择题:
(1)
为了得到函数
的图象,
只需
把余弦曲线上所有的点(
)
(A)
向左平行移动
个单位长度.
(B)
向右平行移动
个单位长度.
(C)
向左平行移动
个单位长度.
(D)
向右平行移动
个单位长度.
C
(2)
为了得到函数
的图象,
只需把余
弦曲线上所有的点的(
)
(A)
横坐标伸长到原来的
5
倍,
纵坐标不变.
(B)
横坐标缩短到原来的
倍,
纵坐标不变.
(C)
纵坐标伸长到原来的
5
倍,
横坐标不变.
(D)
纵坐标缩短到原来的
倍,
横坐标不变.
A
(3)
为了得到函数
的图象,
只需把余
弦曲线上所有的点的(
)
(A)
横坐标伸长到原来的
4
倍,
纵坐标不变.
(B)
横坐标缩短到原来的
倍,
纵坐标不变.
(C)
纵坐标伸长到原来的
4
倍,
横坐标不变.
(D)
纵坐标缩短到原来的
倍,
横坐标不变.
D
2.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
(3)
(4)
解:
(1)
x
y
O
4
-4
p
2p
3p
4p
将正弦曲线的
横坐标伸长
2
倍,
纵坐标伸长4倍.
2.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
(3)
(4)
解:
(2)
x
y
O
将余弦曲线的横
坐标缩为原来的
纵坐标变为原来的
2.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
(3)
(4)
解:
(3)
x
y
O
3
-3
将
y=sinx
的图象向左
平移
得一周期的左端点
是
右端点是
再将
各点的横坐标缩为原来的
得一周期的左端点是
右端点是
再将
y
坐标扩大为原来的
3
倍.
2.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
(3)
(4)
解:
(4)
x
y
O
2
-2
将
y=cosx
的图象向右
平移
得一周期的左端点
是
右端点是
再将各
点的横坐标伸长为原来的2倍,
得一周期的左端点是
右端点是
再将
y
坐标扩大为原来的
2
倍.
(第二课时)
返回目录
1.
简谐运动中的振幅、频率、相位、初相是什么?
在函数
y=Asin(wx+j)
中,
振幅、频率、相位、初相分别由哪些数值确定?
2.
你能由图象确定函数
y=Asin(wx+j)
的常数
A、w、j
的值吗?
物理中简谐运动的图象,
其解析式就是函数
其中A>0,
w
>0.
A是这个简谐运动的振幅,
确定运动物体离开平
衡位置的最大距离.
w
确定周期和频率,
wx+j
称为相位,
j
为初相,
即
x=0
时的相位.
例2.
如图是某简谐运动的图象.
试根据图象回答下列问题:
(1)
这个简谐运动的振幅、周期与频率各是多少?
(2)
从O点算起,
到曲线上的哪一点,
表示完成了一次往复运动?
如从A点算起呢?
(3)
写出这个简谐运动的函数表达式.
解:
振幅
A=
2
cm,
2
x/s
y/cm
O
·
·
·
B
D
F
A
C
E
0.4
0.8
1.2
(1)
周期
T
=
0.8
s,
频率
f
=
(2)
从O点算起,
到D点
表示完成了一次往复运动.
从A点算起,
到E点表示完成了一次往复运动.
例2.
如图是某简谐运动的图象.
试根据图象回答下列问题:
(1)
这个简谐运动的振幅、周期与频率各是多少?
(2)
从O点算起,
到曲线上的哪一点,
表示完成了一次往复运动?
如从A点算起呢?
(3)
写出这个简谐运动的函数表达式.
解:
2
x/s
y/cm
O
·
·
·
B
D
F
A
C
E
0.4
0.8
1.2
(3)
由(1)得
A=2,
初相
j
=
0,
∴函数的表达式为
练习:
(课本55页)
第
3、4
题.
3.
函数
的振幅、周期和频率各
是多少?
它的图象与正弦曲线有什么关系?
答:
=
4p.
图象可由正弦曲线变化而得:
然后将各点的
x
坐标伸长为原来的2倍,
再将各点的
y
坐标缩为原
将正弦曲线向右平移
个单位,
来的
即得
的图象.
x
y
O
1
-1
p
2p
3p
4.
函数
的初相是多少?
它的图象与正弦曲线有什么关系?
答:
函数的初相是
它的图象是由正弦曲线的一部分变化得到的.
∵
x≥0,
∴
函数的图象是由正弦曲线上
x≥
的部分
向左平移
得到的,
如图
例(补充).
已知函数
f(x)=Asin(wx+j)
(A>0)
的图象如图所示,
则振幅
A=
.
x
y
O
分析图象的要点:
(1)
周期;
(2)
对称轴,
对称中心;
(3)
振幅;
(4)
已知点,
特殊点;
(5)
单调性,
奇偶性;
(6)
函数值的正负,
范围.
此图有三个已知点,
其中两个点可以确定周期.
例(补充).
已知函数
f(x)=Asin(wx+j)
(A>0)
的图象如图所示,
则振幅
A=
.
x
y
O
解:
解得
w
=3.
由图象知
图象与
x
轴交于
则
得
图象过另一点
即
而
A>0,
练习(补充)
已知函数
y=sin(wx+j)
(w>0,
-p≤j的图象如图所示,
则
j
=
.
x
y
O
1
-1
2p
解:
由图可得半周期
解得
曲线过点
(2p,
1),
则
解得
∵-p≤j∴k=1
时,
【课时小结】
w
确定周期和频率,
wx+j
称为相位,
j
为初相,
即
x=0
时的相位.
1.
y=Asin(wx+j)
中的物理量
周期
频率
【课时小结】
2.
由图象确定
y=Asin(wx+j)
中的
A、w、j
(1)
周期;
(2)
对称轴,
对称中心;
(3)
振幅;
(4)
特殊点,
已知点;
(5)
单调性,
奇偶性;
(6)
函数值的正负,
范围.
练习与习题
补充1.
将函数
f(x)=sin(wx+j)
的图象向左平移
个单
位,
若所得的图象与原图象重合,
则
w
的值不可能等于
(
)
(A)
2
(B)
6
(C)
8
(D)
12
补充2.
已知函数
y=sin(wx+j)
(w>0,
)
的部分图象如图所示,
则
(
)
(A)
(B)
(C)
(D)
x
y
O
1
习题
1.5
A
组
第
3、4、5
题.
B
组
第
1、2、3
题.
补充1.
将函数
f(x)=sin(wx+j)
的图象向左平移
个单位,
若所得的图象与原图象重合,
则
w
的值不可能等于
(
)
(A)
4
(B)
6
(C)
8
(D)12
分析:
平移后两图象重合,
即
得
w=4k
(k?Z).
则图象平移了
k
(k?Z)
个周期.
所以
w
不可能等于
6.
B
补充2.
已知函数
y=sin(wx+j)
(w>0,
)
的部分图象如图所示,
则
(
)
(A)
(B)
(C)
(D)
x
y
O
1
分析:
到
是
周期.
解得
w=2.
曲线经过点
则
得
∴取
k=1
时,
D
3.
不画图,
直接写出下列函数的振幅、周期与初相,
并说明这些函数的图象可由正弦曲线经过怎样的变化得到
(注意定义域):
(1)
(2)
解:
(1)
振幅
A=8,
周期
=8p.
初相
然后将各点的
x
坐标伸长为原来的4倍,
再将各点的
y
坐标伸长为原来的
8
倍,
即得所求函数的图象.
由正弦曲线
x≥
的部分向右平移
个单位,
习题
1.5
A
组
3.
不画图,
直接写出下列函数的振幅、周期与初相,
并说明这些函数的图象可由正弦曲线经过怎样的变化得到
(注意定义域):
(1)
(2)
解:
(2)
周期
初相
再将各点的
由正弦曲线
x≥
的部分向左平移
个单位,
振幅
然后将各点的
x
坐标缩短为原来的
y
坐标也缩短为原来的
即得所求函数的图象.
习题
1.5
A
组
4.
如图的电流
i
(单位:
A)
随时间
t
(单位:
s)
变化的函数关系是
(1)
求电流
i
变化的周期、频率、振幅及初相;
(2)
当
t
=
0,
(单位:
s
)时,
求电流
i.
解:
(1)
周期
频率
振幅
A
=
5(A).
初相
=
50.
4.
如图的电流
i
(单位:
A)
随时间
t
(单位:
s)
变化的函数关系是
(1)
求电流
i
变化的周期、频率、振幅及初相;
(2)
当
t
=
0,
(单位:
s
)时,
求电流
i.
解:
(2)
=5(A).
=0(A).
=
-5(A).
=0(A).
5.
一根长为
l
cm
的线,
一端固定,
另一端悬挂一个小球,
小球摆动时,
离开平衡位置的位移
s
(单位:
cm)
与时间
t
(单位:
s)
的函数关系是
(1)
求小球摆动的周期;
(2)
已知
g=980
cm/s2,
要使小球摆动的周期是
1
s,
线的长度
l
应当是多少?
(精确到0.1
cm).
解:
(1)
周期
(2)
当T=1时,
解得
≈24.8(cm).
答:
周期为
1
秒时,
线长约为24.8厘米.
B
组
1.
弹簧振子的振动是简谐运动.
下表给出了振子在完成一次全振动过程中的时间
t
与位移
S
之间的对应数据,
根据这些数据求出这个振子的振动函数解析式.
t
0
t0
2t0
3t0
4t0
5t0
S
-20.0
-17.8
-10.1
0.1
10.3
17.7
6t0
7t0
8t0
9t0
10t0
11t0
12t0
20.0
17.7
10.3
0.1
-10.1
-17.8
-20.0
解:
简谐运动的解析式为
S=Asin(wt+j).
由表知周期
T=12t0,
得
振幅
A=20;
t=0
时的相位是初相,
即
S(0)=20sinj
=
-20,
得振子的振动函数解析式为
2.
弹簧挂着的小球作上下运动,
它在
t
秒时相对于平衡位置
(就是静止时的位置)
的高度
h
厘米由下列关系式确定:
以
t
为横坐标,
h
为纵坐标,
作出这个函数在一个周期的闭区间上的图象,
并回答下列问题:
(1)
小球在开始振动时
(即
t
=
0)
的位置在哪里?
(2)
小球的最高点和最低点与平衡位置的距离分别是多少?
(3)
经过多少时间小球往复运动一次?
(4)
每秒钟小球能往复振动多少次?
解:
函数的图象如图:
(1)
(2)
A=2(cm).
T=2p
(s).
(3)
(4)
t
h
O
2
-2
3.
如图,
点
P
是半径为
r
cm
的砂轮边缘上的一个质点,
它从初始位置
P0
开始,
按逆时针方向以角速度
w
rad/s
做圆周运动.
求点
P
的纵坐标
y
关于时间
t
的函数关系,
并求点
P
的运动周期和频率.
x
y
O
·
·
P0
P
j
w
t
解:
M
如图,
P点的纵坐标为
有向线段MP的数量,
即
y
=
MP
=
r
sin(wt+j),
P
的运动周期为
频率为
t≥0.
本章内容
1.1
任意角和弧度制
1.2
任意角的三角函数
1.3
三角函数的诱导公式
1.4
三角函数的图象与性质
1.5
函数
y=Asin(wx+j)
的图象
1.6
三角函数模型的简单应用
第一章
小结
函数
y=Asin(wx+j)
的图象
第一课时
第二课时
(第一课时)
返回目录
2.
函数
y=Asin(wx+j)
的图象可由正弦曲线
y=sinx
怎么变化得来?
1.
函数
y=sin3x
的图象可由
y=sinx
的图象怎样变化得来?
与
y=3sinx
的图象呢?
1.
y=sinx
与
y=sin(x+j)
画出
y
=
sinx
与
y
=
sin(x+
)
的图象.
x
y
o
2p
p
y=sinx
的图象完全一样,
只是
位置不同.
可看出
的图象可由
y
=
sinx
的图象向左平移
个单位得到.
再设
画
的图象.
的图象可由
y
=
sinx
的图象向右
平移
个单位得到.
设
j
=
一般地,
函数
y
=
sin(x+j),
x?R
(其中j
?
0)
的图象,
可以看作把正弦曲线上所有的点向左
(当j>0时)
或向右
(当j<0时)
平行移动
|
j
|
个单位长度而得到.
(初始位置变化)
左右平移
结论:
左
加
右
减
2.
y=sinx
与
y=sinwx
设
w
=2,
画出
y=sinx
和
y=sin2x
的图象.
1
x
y
o
6p
3p
2p
p
y=sinx
y=sin2x
-1
两函数的
y
相等时,
y=sin2x
各点的横坐标恰是
y=sinx
的横坐标的一半,
即将
y=sinx
的图象上各点
的
x
坐标缩为原来的
就得
y=sin2x
的图象.
又设
画出
的图象.
可看出,
将
y=sinx
图象上每一点的
x
坐标伸长
为原来的
3
倍,
即得
的图象.
一般地,
函数
y
=
sinwx,
x?R
(其中w
>0且w≠1)
的图象,
可以看作把正弦曲线上所有点的横坐标缩短
(当w
>1时)
或伸长
(当0
倍
(
纵坐
标不变
)
而得到.
(周期变化)
结论:
x
坐标的伸缩
w
>1,
缩短,
w
<1,
伸长,
3.
y=sinx
与
y=Asinx
设
A
=2,
画出
y=sinx
和
y=2sinx
的图象.
x
y
o
y=sinx
y=2sinx
2
-2
1
-1
p
2p
在
x
坐标相同的情况下,
y=2sinx
图象上各点的
y
坐标
是
y=sinx
的
2
倍.
将
y=sinx
的图象沿
y
轴
方向伸长到原来的
2
倍即得
y=2sinx的图象.
又设
画函数
的图象.
将
y=sinx
的图象沿
y
轴方向缩短为原来的
便得到
的图象.
一般地,
函数
y=Asinx
,
x?R
(其中A>0,
且A≠1)
的图象,
可以看作把正弦曲线上所有点的纵坐标伸长
(
当
A>1
时
)
或缩短
(当
0
A
倍
(横坐标不变)
而得到.
函数
y=Asinx,
x?R的值域是
[
-A,
A
],
最大值是A,
最小值是
-A.
(值域变化)
结论:
y
坐标的伸缩
A
>1,
伸长,
A
<1,
缩短.
综合结论:
一般地,
函数
y=Asin(wx+j),
x?R
(其中A>0,
w>0)的图象,
可以看作用下面的方法得到:
先把正弦曲线上所有的点向左
(当
j>0
时)
或向右
(
当j<0
时
)
平行移动
|
j
|
个单位长度,
再把所得各点的横坐标缩短
(当
w>1
时)
或伸长
(当0
倍
(纵坐标不变),
再把所得各点的纵坐标伸长
(当
A>1时)
或缩短
(当0
(横坐标不变).
例
1.
画出函数
的简图.
画法:
1.
画出
y
=
sinx
的简图;
2.
将
y
=
sinx
的图象向右平移
个单位得到
p
2p
1
-1
y
O
x
例
1.
画出函数
的简图.
画法:
1.
画出
y
=
sinx
的简图;
y
O
p
2p
1
-1
x
p
标伸长为原来的
3
倍,
得到
3.
又将
的图象的
y
坐标不变,
x
坐
例
1.
画出函数
的简图.
画法:
1.
画出
y
=
sinx
的简图;
x
y
O
p
2p
1
-1
标伸长为原来的
3
倍,
得到
3.
又将
的图象的
y
坐标不变,
x
坐
5p
例
1.
画出函数
的简图.
画法:
1.
画出
y
=
sinx
的简图;
x
y
O
p
2p
1
-1
5p
4.
再将
的图象的
x
坐标不变,
y
坐
标伸长为原来的
2
倍,
得到
2
-2
变化顺序:
平移,
x
伸缩,
y
伸缩.
练习:
(课本55页)
第
1、2
题.
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
(1)
x
y
O
p
2p
练习:
(课本55页)
将
y=sinx
的图象上各点
的
y
坐标压缩为原来的一半
即得
的图象.
1
-1
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
五点法:
(1)
x
y
0
p
2p
0
0
0
x
y
O
p
2p
练习:
(课本55页)
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
(2)
x
y
O
练习:
(课本55页)
将
y=sinx
的图象上各点
即得
y=sin3x
的图象.
的
x
坐标压缩为原来的
p
2p
1
-1
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
(3)
x
y
O
1
-1
练习:
(课本55页)
将
y=sinx
的图象向右
平移
个单位即得
的图象.
p
2p
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
(4)
x
y
O
练习:
(课本55页)
将
y=sinx
的图象向右
平移
个单位,
再将各点
的
x
坐标压缩为原来的
再将各点的
y
坐标伸长为
原来的
2
倍即得.
p
2p
1
-1
2
-2
1.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
y=sin3x;
(3)
(4)
解:
五点法:
(4)
y
0
p
2p
0
0
0
x
y
O
x
2
-2
2
-2
练习:
(课本55页)
2.
选择题:
已知函数
的图象为C.
(1)
为了得到函数
的图象,
只要把
C
上所有的点(
).
(A)
向右平行移动
个单位长度.
(B)
向左平行移动
个单位长度.
(C)
向右平行移动
个单位长度.
(D)
向左平行移动
个单位长度.
左加右减,
C
向右移
2.
选择题:
已知函数
的图象为C.
(2)
为了得到函数
的图象,
只要把
C
上所有的点(
).
(A)
横坐标伸长到原来的
2
倍,
纵坐标不变.
(B)
横坐标缩短到原来的
倍,
纵坐标不变.
(C)
纵坐标伸长到原来的
2
倍,
横坐标不变.
(D)
纵坐标缩短到原来的
倍,
横坐标不变.
w>1,
横坐标缩短,
w<1,
横坐标伸长.
B
2.
选择题:
已知函数
的图象为C.
(3)
为了得到函数
的图象,
只要把
C
上所有的点(
).
(A)
横坐标伸长到原来的
倍,
纵坐标不变.
(B)
横坐标缩短到原来的
倍,
纵坐标不变.
(C)
纵坐标伸长到原来的
倍,
横坐标不变.
(D)
纵坐标缩短到原来的
倍,
横坐标不变.
A>1,
纵坐标伸长,
A<1,
纵坐标缩短.
4>3,
伸长
C
【课时小结】
函数
y
=
sin(x+j)
的图象,
可由正弦曲线
y=sinx
的图象向左
(j>0)
或向右
(j<0)
平行移动
|j|
个单位长度而得到.
左
加
右
减
1.
平移
【课时小结】
2.
横向伸缩
函数
y
=
sinwx
(w
>0)
的图象,
可由正弦曲线y=sinx
上所有点的横坐标缩短
(w
>1)
或伸长
(w<1)
到原来的
倍
(
纵坐标不变
)
而得到.
(周期变化)
【课时小结】
3.
纵向伸缩
函数
y
=
Asinx
(A
>0)
的图象,
可由正弦曲线y=sinx
上所有点的纵坐标伸长(A
>1)
或缩短(A<1)
到原来的
A
倍
(
横坐标不变
)
而得到.
【课时小结】
4.
y=Asin(wx+j)
的图象
函数
y=Asin(wx+j)
(A>0,
w>0)的图象,
可用下面的方法得到:
先把正弦曲线上所有的点横向(左加右减)平行移动
|
j
|
个单位长度,
再把所得各点的横坐标伸
缩到原来的
倍
(纵坐标不变),
再把所得各点的纵坐
标伸缩到原来的A倍
(横坐标不变).
习题
1.5
A
组
第
1、2
题.
习题
1.5
A
组
1.
选择题:
(1)
为了得到函数
的图象,
只需
把余弦曲线上所有的点(
)
(A)
向左平行移动
个单位长度.
(B)
向右平行移动
个单位长度.
(C)
向左平行移动
个单位长度.
(D)
向右平行移动
个单位长度.
C
(2)
为了得到函数
的图象,
只需把余
弦曲线上所有的点的(
)
(A)
横坐标伸长到原来的
5
倍,
纵坐标不变.
(B)
横坐标缩短到原来的
倍,
纵坐标不变.
(C)
纵坐标伸长到原来的
5
倍,
横坐标不变.
(D)
纵坐标缩短到原来的
倍,
横坐标不变.
A
(3)
为了得到函数
的图象,
只需把余
弦曲线上所有的点的(
)
(A)
横坐标伸长到原来的
4
倍,
纵坐标不变.
(B)
横坐标缩短到原来的
倍,
纵坐标不变.
(C)
纵坐标伸长到原来的
4
倍,
横坐标不变.
(D)
纵坐标缩短到原来的
倍,
横坐标不变.
D
2.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
(3)
(4)
解:
(1)
x
y
O
4
-4
p
2p
3p
4p
将正弦曲线的
横坐标伸长
2
倍,
纵坐标伸长4倍.
2.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
(3)
(4)
解:
(2)
x
y
O
将余弦曲线的横
坐标缩为原来的
纵坐标变为原来的
2.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
(3)
(4)
解:
(3)
x
y
O
3
-3
将
y=sinx
的图象向左
平移
得一周期的左端点
是
右端点是
再将
各点的横坐标缩为原来的
得一周期的左端点是
右端点是
再将
y
坐标扩大为原来的
3
倍.
2.
画出下列函数在长度为一个周期的闭区间上的简图:
(1)
(2)
(3)
(4)
解:
(4)
x
y
O
2
-2
将
y=cosx
的图象向右
平移
得一周期的左端点
是
右端点是
再将各
点的横坐标伸长为原来的2倍,
得一周期的左端点是
右端点是
再将
y
坐标扩大为原来的
2
倍.
(第二课时)
返回目录
1.
简谐运动中的振幅、频率、相位、初相是什么?
在函数
y=Asin(wx+j)
中,
振幅、频率、相位、初相分别由哪些数值确定?
2.
你能由图象确定函数
y=Asin(wx+j)
的常数
A、w、j
的值吗?
物理中简谐运动的图象,
其解析式就是函数
其中A>0,
w
>0.
A是这个简谐运动的振幅,
确定运动物体离开平
衡位置的最大距离.
w
确定周期和频率,
wx+j
称为相位,
j
为初相,
即
x=0
时的相位.
例2.
如图是某简谐运动的图象.
试根据图象回答下列问题:
(1)
这个简谐运动的振幅、周期与频率各是多少?
(2)
从O点算起,
到曲线上的哪一点,
表示完成了一次往复运动?
如从A点算起呢?
(3)
写出这个简谐运动的函数表达式.
解:
振幅
A=
2
cm,
2
x/s
y/cm
O
·
·
·
B
D
F
A
C
E
0.4
0.8
1.2
(1)
周期
T
=
0.8
s,
频率
f
=
(2)
从O点算起,
到D点
表示完成了一次往复运动.
从A点算起,
到E点表示完成了一次往复运动.
例2.
如图是某简谐运动的图象.
试根据图象回答下列问题:
(1)
这个简谐运动的振幅、周期与频率各是多少?
(2)
从O点算起,
到曲线上的哪一点,
表示完成了一次往复运动?
如从A点算起呢?
(3)
写出这个简谐运动的函数表达式.
解:
2
x/s
y/cm
O
·
·
·
B
D
F
A
C
E
0.4
0.8
1.2
(3)
由(1)得
A=2,
初相
j
=
0,
∴函数的表达式为
练习:
(课本55页)
第
3、4
题.
3.
函数
的振幅、周期和频率各
是多少?
它的图象与正弦曲线有什么关系?
答:
=
4p.
图象可由正弦曲线变化而得:
然后将各点的
x
坐标伸长为原来的2倍,
再将各点的
y
坐标缩为原
将正弦曲线向右平移
个单位,
来的
即得
的图象.
x
y
O
1
-1
p
2p
3p
4.
函数
的初相是多少?
它的图象与正弦曲线有什么关系?
答:
函数的初相是
它的图象是由正弦曲线的一部分变化得到的.
∵
x≥0,
∴
函数的图象是由正弦曲线上
x≥
的部分
向左平移
得到的,
如图
例(补充).
已知函数
f(x)=Asin(wx+j)
(A>0)
的图象如图所示,
则振幅
A=
.
x
y
O
分析图象的要点:
(1)
周期;
(2)
对称轴,
对称中心;
(3)
振幅;
(4)
已知点,
特殊点;
(5)
单调性,
奇偶性;
(6)
函数值的正负,
范围.
此图有三个已知点,
其中两个点可以确定周期.
例(补充).
已知函数
f(x)=Asin(wx+j)
(A>0)
的图象如图所示,
则振幅
A=
.
x
y
O
解:
解得
w
=3.
由图象知
图象与
x
轴交于
则
得
图象过另一点
即
而
A>0,
练习(补充)
已知函数
y=sin(wx+j)
(w>0,
-p≤j
则
j
=
.
x
y
O
1
-1
2p
解:
由图可得半周期
解得
曲线过点
(2p,
1),
则
解得
∵-p≤j
时,
【课时小结】
w
确定周期和频率,
wx+j
称为相位,
j
为初相,
即
x=0
时的相位.
1.
y=Asin(wx+j)
中的物理量
周期
频率
【课时小结】
2.
由图象确定
y=Asin(wx+j)
中的
A、w、j
(1)
周期;
(2)
对称轴,
对称中心;
(3)
振幅;
(4)
特殊点,
已知点;
(5)
单调性,
奇偶性;
(6)
函数值的正负,
范围.
练习与习题
补充1.
将函数
f(x)=sin(wx+j)
的图象向左平移
个单
位,
若所得的图象与原图象重合,
则
w
的值不可能等于
(
)
(A)
2
(B)
6
(C)
8
(D)
12
补充2.
已知函数
y=sin(wx+j)
(w>0,
)
的部分图象如图所示,
则
(
)
(A)
(B)
(C)
(D)
x
y
O
1
习题
1.5
A
组
第
3、4、5
题.
B
组
第
1、2、3
题.
补充1.
将函数
f(x)=sin(wx+j)
的图象向左平移
个单位,
若所得的图象与原图象重合,
则
w
的值不可能等于
(
)
(A)
4
(B)
6
(C)
8
(D)12
分析:
平移后两图象重合,
即
得
w=4k
(k?Z).
则图象平移了
k
(k?Z)
个周期.
所以
w
不可能等于
6.
B
补充2.
已知函数
y=sin(wx+j)
(w>0,
)
的部分图象如图所示,
则
(
)
(A)
(B)
(C)
(D)
x
y
O
1
分析:
到
是
周期.
解得
w=2.
曲线经过点
则
得
∴取
k=1
时,
D
3.
不画图,
直接写出下列函数的振幅、周期与初相,
并说明这些函数的图象可由正弦曲线经过怎样的变化得到
(注意定义域):
(1)
(2)
解:
(1)
振幅
A=8,
周期
=8p.
初相
然后将各点的
x
坐标伸长为原来的4倍,
再将各点的
y
坐标伸长为原来的
8
倍,
即得所求函数的图象.
由正弦曲线
x≥
的部分向右平移
个单位,
习题
1.5
A
组
3.
不画图,
直接写出下列函数的振幅、周期与初相,
并说明这些函数的图象可由正弦曲线经过怎样的变化得到
(注意定义域):
(1)
(2)
解:
(2)
周期
初相
再将各点的
由正弦曲线
x≥
的部分向左平移
个单位,
振幅
然后将各点的
x
坐标缩短为原来的
y
坐标也缩短为原来的
即得所求函数的图象.
习题
1.5
A
组
4.
如图的电流
i
(单位:
A)
随时间
t
(单位:
s)
变化的函数关系是
(1)
求电流
i
变化的周期、频率、振幅及初相;
(2)
当
t
=
0,
(单位:
s
)时,
求电流
i.
解:
(1)
周期
频率
振幅
A
=
5(A).
初相
=
50.
4.
如图的电流
i
(单位:
A)
随时间
t
(单位:
s)
变化的函数关系是
(1)
求电流
i
变化的周期、频率、振幅及初相;
(2)
当
t
=
0,
(单位:
s
)时,
求电流
i.
解:
(2)
=5(A).
=0(A).
=
-5(A).
=0(A).
5.
一根长为
l
cm
的线,
一端固定,
另一端悬挂一个小球,
小球摆动时,
离开平衡位置的位移
s
(单位:
cm)
与时间
t
(单位:
s)
的函数关系是
(1)
求小球摆动的周期;
(2)
已知
g=980
cm/s2,
要使小球摆动的周期是
1
s,
线的长度
l
应当是多少?
(精确到0.1
cm).
解:
(1)
周期
(2)
当T=1时,
解得
≈24.8(cm).
答:
周期为
1
秒时,
线长约为24.8厘米.
B
组
1.
弹簧振子的振动是简谐运动.
下表给出了振子在完成一次全振动过程中的时间
t
与位移
S
之间的对应数据,
根据这些数据求出这个振子的振动函数解析式.
t
0
t0
2t0
3t0
4t0
5t0
S
-20.0
-17.8
-10.1
0.1
10.3
17.7
6t0
7t0
8t0
9t0
10t0
11t0
12t0
20.0
17.7
10.3
0.1
-10.1
-17.8
-20.0
解:
简谐运动的解析式为
S=Asin(wt+j).
由表知周期
T=12t0,
得
振幅
A=20;
t=0
时的相位是初相,
即
S(0)=20sinj
=
-20,
得振子的振动函数解析式为
2.
弹簧挂着的小球作上下运动,
它在
t
秒时相对于平衡位置
(就是静止时的位置)
的高度
h
厘米由下列关系式确定:
以
t
为横坐标,
h
为纵坐标,
作出这个函数在一个周期的闭区间上的图象,
并回答下列问题:
(1)
小球在开始振动时
(即
t
=
0)
的位置在哪里?
(2)
小球的最高点和最低点与平衡位置的距离分别是多少?
(3)
经过多少时间小球往复运动一次?
(4)
每秒钟小球能往复振动多少次?
解:
函数的图象如图:
(1)
(2)
A=2(cm).
T=2p
(s).
(3)
(4)
t
h
O
2
-2
3.
如图,
点
P
是半径为
r
cm
的砂轮边缘上的一个质点,
它从初始位置
P0
开始,
按逆时针方向以角速度
w
rad/s
做圆周运动.
求点
P
的纵坐标
y
关于时间
t
的函数关系,
并求点
P
的运动周期和频率.
x
y
O
·
·
P0
P
j
w
t
解:
M
如图,
P点的纵坐标为
有向线段MP的数量,
即
y
=
MP
=
r
sin(wt+j),
P
的运动周期为
频率为
t≥0.
