2020-2021学年高一数学人教A版必修4第一章1.1 任意角和弧度制4课时课件( 共112张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修4第一章1.1 任意角和弧度制4课时课件( 共112张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 00:00:00 | ||
图片预览








文档简介
第一章 三角函数
人民教育出版社 |必修四
本章内容
1.1 任意角和弧度制
1.2 任意角的三角函数
1.3 三角函数的诱导公式
1.4 三角函数的图象与性质
1.5 函数 y=Asin(wx+j) 的图象
1.6 三角函数模型的简单应用
第一章 小结
1.1.1 任意角(第一课时)
复习与提高
1.1.1 任意角(第二课时)
1.1.2 弧度制
1.1 任意角和弧度制
1.1.1 任意角
(第一课时)
返回目录
1. 什么是正角、负角、零角?
2. 什么是象限角? 什么样的角又不属于象限角?
3. 什么是同终边的角? 怎样找出同终边的角?
学
习
要
点
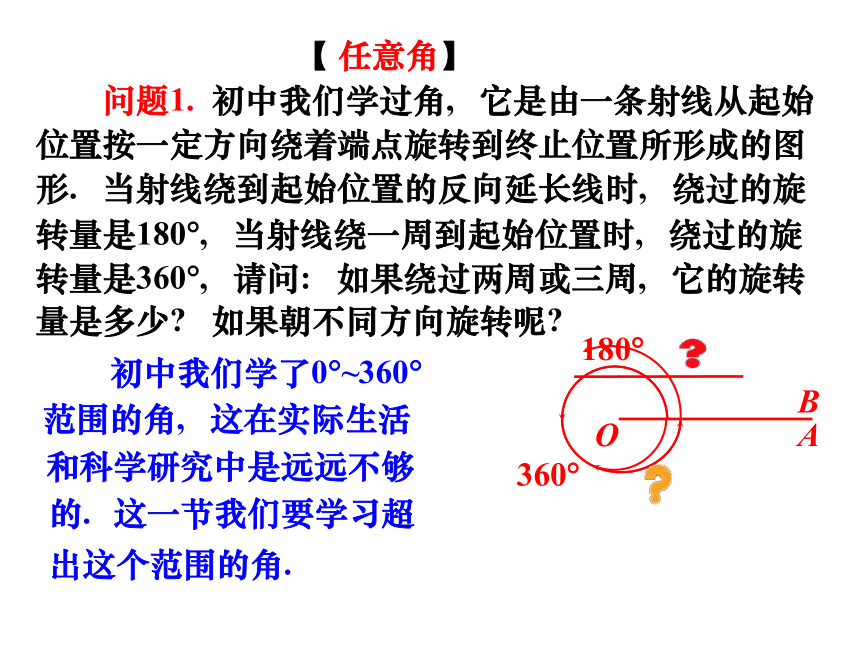
问题1. 初中我们学过角, 它是由一条射线从起始位置按一定方向绕着端点旋转到终止位置所形成的图形. 当射线绕到起始位置的反向延长线时, 绕过的旋转量是180?, 当射线绕一周到起始位置时, 绕过的旋转量是360?, 请问: 如果绕过两周或三周, 它的旋转量是多少? 如果朝不同方向旋转呢?
【 任意角】
初中我们学了0?~360?
范围的角, 这在实际生活
和科学研究中是远远不够
的.
这一节我们要学习超
出这个范围的角.
O
A
B
180?
360?
1. 正角, 任意大的正角.
规定:
按逆时针方向旋转形成的角叫做正角.
随着终边的旋转, 角可以是 0?~360? 范围内的, 也可以是大于360?的任意大的角.
2. 负角, 任意的负角.
按顺时针方向旋转形成的角叫做负角.
随着终边的顺时针旋转, 角可以是任意的负角.
规定:
1. 正角, 任意大的正角.
规定:
按逆时针方向旋转形成的角叫做正角.
随着终边的旋转, 角可以是 0?~360? 范围内的, 也可以是大于360?的任意大的角.
2. 负角, 任意的负角.
按顺时针方向旋转形成的角叫做负角.
随着终边的顺时针旋转, 角可以是任意的负角.
规定:
角一般用字母 a, b 等希腊字母表示.
在不引起混淆时, 一般省略角符号 “∠”, 简记为 “角a ” 或 “a ”.
3. 零角.
如果一条射线没有作任何旋转, 我们称它形成了零角.
问题2. 零角的终边与始边重合吗 ? 终边与始边重合的角是零角吗 ?
零角的终边与始边重合.
终边与始边重合的角不一定是零角.
终边与始边重合
O
0?
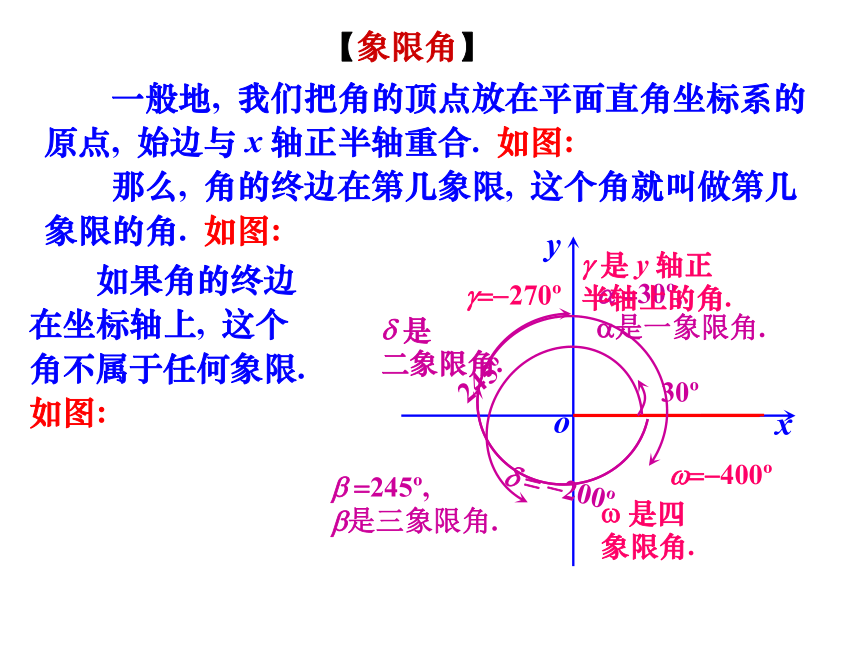
【象限角】
一般地, 我们把角的顶点放在平面直角坐标系的原点, 始边与 x 轴正半轴重合. 如图:
那么, 角的终边在第几象限, 这个角就叫做第几象限的角. 如图:
x
y
o
a =30?,
a是一象限角.
30?
245?
b =245?,
b是三象限角.
g=-270?
g 是 y 轴正
半轴上的角.
d = -200?
d 是
二象限角.
w=-400?
w 是四
象限角.
如果角的终边在坐标轴上, 这个角不属于任何象限. 如图:
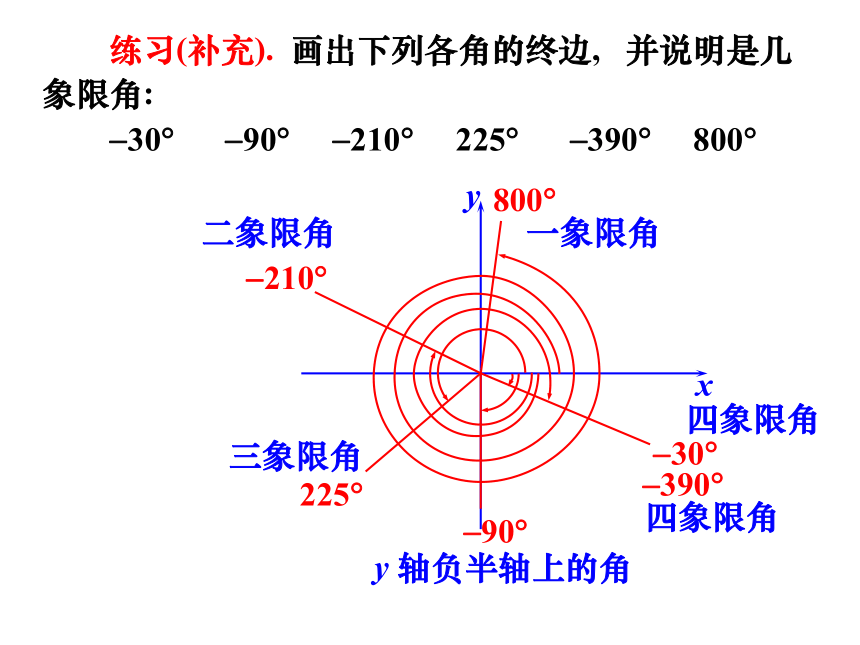
练习(补充). 画出下列各角的终边, 并说明是几象限角:
-30? -90? -210? 225? -390? 800?
x
y
-90?
800?
225?
-210?
-390?
-30?
四象限角
y 轴负半轴上的角
二象限角
三象限角
四象限角
一象限角
【同终边的角】
问题3. 30?角和390?角始边相同的时候, 终边是否重合? 30?角和-30?角始边相同的时候, 终边是否重合? 你能说出几个与-30?角始边相同, 且终边重合的角吗?
始边
终边
O
30?
-30?
终边
390?
始边相同时,
30?与390?的终边相同,
30?与-30?的终边不相同.
设角 a 是 0?~360?之间的角时, 与 a 同终边的角写成
k·360?+a, k?Z.
例1. 在 0?~360? 范围内, 找出与 -950?12? 角终边相同的角, 并判定它是第几象限角.
分析:
-950?12? 是顺时针旋转两周又230?12?,
x
y
O
也可顺时针旋转三周又
逆时针旋转129?48?.
-360?
-720?
-230?12?
-1080?
129?48?
∴在 0?~360? 范围内与
-950?12? 同终边的角是 129?48?.
即 -950?12?= -2?360?-230?12?.
-950?12?与 -230?12? 同终边.
即 -950?12?= -3?360?+129?48?.
-950?12?与 129?48? 同终边.
-1080?
例1. 在 0?~360? 范围内, 找出与 -950?12? 角终边相同的角, 并判定它是第几象限角.
x
y
O
129?48?
任一个角 b 都可以写成
k·360?+a 的形式,
k?Z, a 是 0?~360? 间的角.
即 b = k·360?+a, 其中
则 b 与 a 同终边.
(补充). 在 0?~360? 范围内, 找出与下列各角终边相同的角, 并指出它们是第几角象限角:
(1) -750?; (2) 1000?28?.
练习(课本5页)
第 1、2 题
练习: (课本5页)
1. (口答) 锐角是第几象限角? 第一象限角一定是锐角吗? 再分别就直角、钝角来回答这两个问题.
锐角是第一象限角.
第一象限角不一定是锐角.
直角终边与 y 轴非负半轴重合, 不属任何象限角.
钝角是第二象限角, 但第二象限角不一定是钝角.
2. (口答) 今天是星期三, 那么7k (k?Z)天后的那一天是星期几? 7k (k?Z)天前的那一天是星期几? 100天后的那一天是星期几?
今天是星期三, 那么7k (k?Z)天后的那一天
星期是以7天为周期循环出现的.
也是星期三,
7k (k?Z)天前的那一天也是星期三.
100=14?7+2,
∴ 100天后的那一天是星期五.
(补充). 在 0?~360? 范围内, 找出与下列各角终边相同的角, 并指出它们是第几角象限角:
(1) -750?; (2) 1000?28?.
解:
(1)
∵-750?= 3?(-360?)+330?,
∴在 0?~360? 范围内与角-750?终边相同的角是
330?,
(2)
∵1000?28?= 2?360?+279?32?,
∴在 0?~360? 范围内与角1000?28?终边相同的角
是 279?32?,
它是第四象限角.
它是第四象限角.
【课时小结】
1. 正角、负角、零角
按逆时针方向旋转形成的角叫做正角.
旋转一周后大于360?, 旋转两周后大于720?.
按顺时针方向旋转形成的角叫做负角.
旋转一周后小于-360?, 旋转两周后小于-720?.
一条射线不作任何旋转, 与它自己形成 0? 的角.
零角的终边与始边重合.
终边与始边重合的角不一定是零角.
【课时小结】
2. 象限角
终边在第几象限, 就叫做第几象限的角.
终边在坐标轴上, 不属于任何象限角.
锐角是一象限角.
一象限角不一定是锐角.
钝角是二象限角.
二象限角不一定是钝角.
【课时小结】
3. 同终边的角
始边相同, 终边重合的角.
a 是 0?~360? 内的角, 与 a 同终边的角为
k·360?+a, k?Z.
第 3、4 题.
练习: (课本5页)
3. 已知角的顶点与直角坐标系的原点重合, 始边与 x 轴的非负半轴重合, 作出下列各角, 并指出它们是第几象限的角:
(1) 420?; (2) -75?; (3) 855?; (4) -510?.
x
y
o
420?
855?
-75?
-510?
解:
(1)
420? 是第一象限角.
(2)
-75? 是第四象限角.
(3)
855? 是第二象限角.
(4)
-510? 是第三象限角.
4. 在 0?~360? 范围内, 找出与下列各角终边相同的角, 并指出它们是第几角象限角:
(1) -54?18?; (2) 395?8?; (3) -1190?30?.
解:
(1)
∵-54?18?= -360?+305?42?,
∴在 0?~360? 范围内与角-54?18?终边相同的角是
305?42?,
(2)
∵395?8?= 360?+35?8?,
∴在 0?~360? 范围内与角395?8?终边相同的角是
35?8?,
它是第四象限角.
它是第一象限角.
(3)
∵-1190?30?= -360??4+249?30?,
∴在 0?~360? 范围内与角-1190?30?终边相同的角
是249?30?,
它是第三象限角.
1.1.1 任意角
(第二课时)
返回目录
1. 与一个角 a 同终边的角的集合怎样表示?
2. 终边在 x 轴上的角怎样表示? 终边在 y 轴上的角怎样表示?
3. 终边在某一象限的角怎样表示? 终边在某一范围内的角怎样表示?
学
习
要
点
问题1. 已知角a =30?, 与a 同终边的角还有哪些? 这些角的集合怎样表示?
x
y
o
a =30?
正角:
30?+360?,
30?+2?360?,
30?+3?360?, …
如图,
【同终边的角的集合】
问题1. 已知角a =30?, 与a 同终边的角还有哪些? 这些角的集合怎样表示?
x
y
o
正角:
各角与a 都相差整数个360?.
所有与a 同终边的角, 连同a 在内, 可构成一个集合:
S={ b | b =a + k·360?, k∈Z }.
30?+360?,
30?+2?360?,
30?+3?360?, …
30?-360?,
30?-2?360?,
30?-3?360?, …
负角:
如图,
【同终边的角的集合】
a =30?
例(补充). 已知a 为锐角, 且sina = 画出a 的终边, 并写出与a 同终边的角的集合.
解:
锐角a =45?,
a 的终边与第一象限的
角平分线重合 (如图),
x
y
o
a
与a 同终边的角的集合为
{ b |b =45?+ k?360?, k?Z }.
例2. 写出终边在 y 轴上的角的集合.
解:
在 0?~360? 范围内, 终边在 y 轴上的角有两个,
即 90? 和 270?.
与90?同终边的角的集集合为
S1={b |b =90?+k·360?, k?Z};
与270?同终边的角的集集合为
S2={b |b =270?+k·360?, k?Z}.
合并 S1 与 S2 为:
x
y
o
90?
270?
180?
180?
两条终边构成一个平角,
它们相差 k 个180?,
S = S1∪S2
={b |b = 90?+n·180?, n?Z}.
例3. 写出终边在直线 y = x 上的角的集合 S, 并把 S 中适合不等式-360?≤b <720? 的元素b 写出来.
解:
x
y
o
因为直线 y=x 是第一、
三象限的角平分线,
在 0?~360?
范围内有45?和225?两个角,
45?
225?
这两个角相差 k 个180?,
∴与这两个角同终边的
角的集合为
S = { b | b = 45?+k·180?, k?Z }.
取 k = -2, -1, 0, 1, 2, 3 ,
b 的值分别为
-315?,
45?,
225?,
405?,
585?.
-135?,
要使-360?≤b <720?,
【互为反向延长线的两条终边的角的集合】
x
y
o
a
S = { b | b = a +
{ b | b = a +
∪
= { b | b = a + n?180?, n∈Z }.
k?360?, k∈Z }
180?+k?360?, k∈Z }
与两条互为反向延长线的终边重合的所有角的集合的写法:
={b | b =a+2k?180?, k?Z }
∪{b | b =a+(2k+1)?180?, k?Z}
练习: (补充)
1. 写出终边与 x 轴正、负半轴重合的角的集合.
练习: (课本5页)
5. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-720?≤b <360?的元素 b 写出来:
(1) 1303?18?; (2) -225?.
1. 写出终边与 x 轴正、负半轴重合的角的集合.
x
y
o
解:
终边与 x 轴正半轴重合的是
k?360?,
与 x 轴负半轴重合的是
∴ 终边与 x 轴正、负半轴
S={ b | b = k?180? , k∈Z }.
k?360?+180?,
重合的所有角的集合为
练习: (补充)
练习: (课本5页)
5. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-720?≤b <360?的元素 b 写出来:
(1) 1303?18?; (2) -225?.
解:
S={ b | b = 1303?18?+k·360?, k∈Z },
∴取 k = -5, -4, -3,
-496?42?,
(1)
∵ -720?≤b <360?,
集合中满足条件的元素 b 分别为
-136?42?,
223?18?.
练习: (课本5页)
5. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-720?≤b <360?的元素 b 写出来:
(1) 1303?18?; (2) -225?.
解:
S={ b | b = -225?+k·360?, k∈Z },
∴取 k = -1, 0, 1,
-585?,
(2)
∵ -720?≤b <360?,
集合中满足条件的元素 b 分别为
-225?,
135?.
【终边在某范围内的角的集合】
问题2. 终边与0?~60?间的角重合的角的集合怎样表示? 终边在第二象限的角的集合怎样表示?
< b <
x
y
o
0?
60?
起始位置
终止位置
k·360?
60?+k·360?,
k∈Z }.
{ b |
x
y
o
90?
180?
起始位置
终止位置
90?+k·360?,
180?+k·360?,
集合: { b |90?+k·360?b
b
终边在第二象限:
例 (补充). 已知集合 S={ b | k·360?-45?解:
① 画出 k·360?- 45?的终边,
③ 按逆时针从终边①到
终边②之间的区域就
是角 b 的终边的范围.
如图:
x
y
o
② 画出k·360?+150?的终边,
①
②
k·360?-45?
k·360?+150?
练习(补充). 若 a 是第二象限的角, 则 2a 是第几象限的角? 是第几象限的角?
x
y
o
解:
如图,
用不等式表示a 的范围:
90?+k?360?360?+2k?360?, k∈Z, (如图)
<2a <
180?+2k?360?
180?+k?360?
360?+2k?360?
∴ 2a 是三、四象限及 y 轴负半轴上的角,
即下半平面的角.
45?+k?180?
90?+k?180?, k∈Z,
45?+k?180?
45?+k?180?
90?+k?180?
90?+k?360?
∴ 是一、三象限的角.
180?+2k?360?
90?+k?180?
k∈Z,
计算 2a 的范围:
计算 的范围:
【课时小结】
1. 与角 a 同终边的角的集合
S={ b | b =a + k·360?, k∈Z }.
2. 与角 a 以及 a+180? 同终边的角的集合
{ b | b = a + n?180?, n∈Z }.
与 x 轴重合的终边有两条, 角的集合为
{ b | b = k?180?, k∈Z }.
与 y 轴重合的终边也有两条, 角的集合为
{ b | b = 90?+k?180?, k∈Z }.
【课时小结】
3. 某范围内的角的集合
{g |a+k·360?< gx
y
O
a
b
g
第一象限角的集合
{g |k·360?< g <90?+k·360?, k?Z}.
终边在右半平面内角的集合
{g |-90?+k·360?< g <90?+k·360?, k?Z}.
习题 1.1
A 组
第 1、2、3、5 题.
1. 在0?~360?范围内,找出与下列各角终边相同的角, 并指出它们是哪个象限的角:
(1) -265?; (2) -1000?; (3) -843?10?; (4) 3900?.
解:
(1)
∵-265? = -360?+95?,
∴在0?~360?范围内与-265?终边相同的角是95?.
(2)
∵-1000? = -3?360?+80?,
∴在0?~360?范围内与-1000?终边相同的角是80?.
它们是第二象限的角.
它们是第一象限的角.
习题 1.1
A 组
1. 在0?~360?范围内,找出与下列各角终边相同的角, 并指出它们是哪个象限的角:
(1) -265?; (2) -1000?; (3) -843?10?; (4) 3900?.
解:
(3)
∵-843?10? = -3?360?+236?50?,
∴在0?~360?范围内与-843?10?终边相同的角是236?50?.
(4)
∵3900? = 10?360?+300?,
∴在0?~360?范围内与3900?终边相同的角是300?.
它们是第三象限的角.
它们是第四象限的角.
习题 1.1
A 组
2. 写出终边在 x 轴上的角的集合.
解:
终边在 x 轴上包括正半轴方向和负半轴方向,
这些角与 0? 角相差整数个 180?.
所以终边在 x 轴上的角的集合为
S={b | b = n·180?, n?Z}.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(1)
S={ b | b = 60?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -1, 0,
得满足条件的元素 b 为
-300?,
60?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(2)
S={ b | b = -75?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = 0, 1,
得满足条件的元素 b 为
-75?,
285?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(3)
S={ b | b = - 824?30?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = 2, 3,
得满足条件的元素 b 为
-104?30?,
255?30?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(4)
S={ b | b = 475?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -2, -1,
得满足条件的元素 b 为
-245?,
115?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(5)
S={ b | b = 90?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -1, 0,
得满足条件的元素 b 为
-270?,
90?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(6)
S={ b | b = 270?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -1, 0,
得满足条件的元素 b 为
-90?,
270?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(7)
S={ b | b = 180?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -1, 0,
得满足条件的元素 b 为
-180?,
180?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(8)
S={ b | b = 0?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -1, 0,
得满足条件的元素 b 为
-360?,
0?.
5. 选择题:
(1) 已知 a 是锐角, 那么 2a 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 小于180?的正角 (D) 第一或第二象限角
(2) 已知 a 是第一象限角, 那么 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 第一或第二象限角 (D) 第一或第三象限角
解:
(1)
∵ a 是锐角,
则 0?∴ 0?<2a <180?,
则应选C.
C
5. 选择题:
(1) 已知 a 是锐角, 那么 2a 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 小于180?的正角 (D) 第一或第二象限角
(2) 已知 a 是第一象限角, 那么 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 第一或第二象限角 (D) 第一或第三象限角
解:
(2)
∵ a 是第一象限角,
则 k·360?则应选D.
C
x
y
o
45?
45?
k·180?
k·180?
45?+k·180?
45?+k·180?
得
D
1.1.2
弧度制
返回目录
1. 什么是弧度制? 扇形中的弧长、半径、圆心角的弧度数是怎样的关系?
2. 弧度制与角度制怎样换算?
3. 特殊角的弧度数有什么规律? 你能熟练掌握特殊角的弧度数吗?
学
习
要
点
问题1: 请同学们画一个扇形, 使它的弧长等于半径, 你估计这个扇形的圆心角是多少? 这个圆心角是周角的几分之几?
=1弧度
r
l
a
扇形所在圆的周长为
2p r,
那么圆心角 a 是周角的
即
我们把弧长等于半径的圆心角叫做 1 弧度的角.
用 rad 表示, 读作弧度.
l = r
弧长是周长的
≈57?18?.
=1 rad.
在角度制中, 周角的 是 1 度的角.
在弧度制中, 周角的 是 1 弧度的角.
问题2. 1 周角有多少弧度? 1 弧度有多少度?
1 周角=2p 弧度.
1 弧度≈57?18?.
360?=2p rad,
180?=p rad,
※一般地, 正角的弧度数是一个正数, 负角的弧度数是一个负数, 零角的弧度数是 0. 如果半径为 r 的圆的圆心角 a 所对的弧长为 l, 那么, 角 a 的弧度数的绝对值是
例1. 按照下列要求, 把67?30?化成弧度:
(1) 精确值;
(2) 精确到0.001的近似值.
解:
(1)
∴ 67?30? = 67.5?
(2)
≈1.178 rad.
例2. 将 3.14 rad 换算成角度 (用度数表示, 精确到 0.001).
解:
=179.922?.
今后用弧度制表示角度时, “弧度” 二字或 “rad”通常略去不写, 而只写该角所对应的弧度数.
如角 a =2 表示 a 是 2 rad 的角,
角 表示 b 是 弧度的角.
∵1rad≈57.3?,
∴3.14rad≈57.3??3.14
请填写下表中特殊角的弧度数:
度
0?
30?
45?
60?
90?
120?
135?
150?
180?
270?
360?
弧度
在实际应用中, 常用多少p 弧度表示弧度的精确值.
请记住这些特殊角的弧度数.
0
对于一些特殊角的弧度数要经常用到.
例(补充). 用弧度数表示下列角的集合:
(1) 终边与90?角的终边重合;
(2) 终边与直线 y = x 重合.
解:
(1)
∴ 用弧度制表示终边与90?重合的角的集合为
(2)
∵ 终边与直线 y = x 重合的角的集合为
x
y
o
例4. 利用计算器比较 sin1.5 和 sin85? 的大小.
解:
用计算器求得 sin1.5 ≈0.9974,
sin85?≈0.9962,
∴sin1.5 > sin85?.
练习: (课本9页)
第 1、2 题.
1. 把下列角度化成弧度:
(1) 22?30?; (2) -210?; (3) 1200?.
解:
(1)
∴ 22?30?=22.5?
(2)
(3)
练习: (课本9页)
2. 把下列弧度化成度:
(1) (2) (3)
解:
(1)
=15?.
(2)
= -240?.
(3)
= 54?.
例3. 利用弧度制证明下列关于扇形的公式:
(1) l =a R; (2) (3)
证明:
(1)
∴ l = |a|R,
又a > 0,
∴ l = a R.
(2)
(3)
l
R
(变态三解形)
∵1 弧度是周角的
∴ 1 弧度的扇形面积是圆面积的
则 a 弧度的扇形面积为
l = a R.
R: 半径, l : 弧长, S: 面积,
a : 圆心角的弧度数,
在扇形中,
练习(补充). 已知半径为120 mm的圆上, 有一条弧的长是144 mm, 求此弧所对的圆心角的弧度数, 以及所对扇形的面积.
解:
答: 圆心角是1.2 rad, 扇形的面积是8640 mm2.
【课时小结】
1. 弧度制
用弧度表示角的大小.
弧长等于半径的圆心角叫做 1 弧度的角.
=1弧度
r
l
a
l = r
【课时小结】
2. 弧度与角度的换算
1 周角=2p 弧度.
1 平角=p 弧度.
【课时小结】
3. 特殊角的弧度数
弧度
360?
270?
180?
150?
135?
120?
90?
60?
45?
30?
0?
度
0
【课时小结】
4. 用弧度数表示扇形的弧长与面积
l = a R.
R: 半径, l : 弧长, S: 面积,
a : 圆心角的弧度数,
练习: (课本9页)
第 3、4、5、6 题.
习题 1.1
A 组
第 4、 6、7、8 题.
3. 用弧度表示:
(1) 终边在 x 轴上的集合;
(2) 终边在 y 轴上的集合.
解:
(1)
终边在 x 轴上的集合为:
S={a |a = kp, k?Z}.
(2)
终边在 y 轴上的集合为:
练习: (课本9页)
4. 利用计算器比较下列各对值的大小 (精确到0.001):
(1) cos0.75? 和 cos0.75; (2) tan1.2? 和 tan1.2.
解:
(1)
∵cos0.75?≈1.000,
cos0.75≈0.732,
∴cos0.75?>cos0.75.
(2)
∵tan1.2?≈0.021,
tan1.2≈2.572,
∴tan1.2? 5. 分别用角度制、弧度制下的弧长公式, 计算半径为 1 m 的圆中, 60?的圆心角所对的弧的长度 (可用计算器).
解:
角度制:
弧度制:
≈1.047(m);
∴ l=aR
≈1.05(m).
6. 已知半径为120 mm 的圆上, 有一条弧的长是144 mm, 求该弧所对的圆心角的弧度数.
解:
又 l =144 mm, R=120 mm,
=1.2 (rad).
习题 1.1
A 组
4. 分别用角度和弧度写出第一、二、三、四象限角的集合.
解:
角度表示:
弧度表示:
第一象限角:
第二象限角:
{b |k·360?角度表示:
弧度表示:
{b |90?+k·360?习题 1.1
A 组
4. 分别用角度和弧度写出第一、二、三、四象限角的集合.
解:
角度表示:
弧度表示:
第三象限角:
第四象限角:
角度表示:
弧度表示:
{b |270?+k·360?{b |180?+k·360? 6. 一条弦的长等于半径, 这条弦所对的圆心角等于 1 弧度吗? 为什么?
答: 不等于 1 弧度.
当且仅当 l=r 时, 圆心角
r
l
d
(如图)
才是 1 弧度的角.
而 d=r, l>d,
则 l>r.
∴圆心角不是 1 弧度的角.
7. 把下列各角度化成弧度:
(1) 36?; (2) -150?; (3) 1095?; (4) 1440?.
解:
(1)
(2)
(3)
(4)
= 8p rad.
8. 把下列各弧度化成度:
(1) (2) (3) 1.4; (4)
解:
(1)
= -210?.
(2)
= -600?.
(3)
≈80?12?.
(4)
≈38?12?.
复习与提高
复习与提高
返回目录
1. 任意角
正角、负角、零角
2. 象限角
终边在第几象限, 就叫做第几象限的角.
终边在坐标轴上, 不属于任何象限角.
3. 同终边的角
始边相同, 终边重合的角.
与 a 同终边的角的集合
{b |b =a+k·360?, k?Z}.
与 a 和 a 的反向延长线同终边的角的集合
{b |b =a+k·180?, k?Z}.
知识要点
4. 和某范围内终边相同的角的集合
{g |a+k·360?< gx
y
O
a
b
g
终边在上半平面的角的集合
{g |k·360?< g <180?+k·360?, k?Z}.
终边在右半平面内角的集合
{g |-90?+k·360?< g <90?+k·360?, k?Z}.
知识要点
5. 弧度制
弧长等于半径的圆心角叫做 1 弧度的角.
=1弧度
r
l
a
l = r
6. 弧度与角度的换算
1 周角=2p 弧度.
1 平角=p 弧度.
知识要点
7. 用弧度数表示扇形的弧长与面积
l = a R.
R: 半径, l : 弧长, S: 面积,
a : 圆心角的弧度数,
知识要点
【例题选讲】
例1. 在 0~2p 内, 用角度写出下列各角:
(1)
(2)
(3)
解:
(1)
在 0~2p 内, 取 k=0 时,
=15?.
x
y
O
15?
一条终边.
【例题选讲】
例1. 在 0~2p 内, 用角度写出下列各角:
(1)
(2)
(3)
解:
(2)
在 0~2p 内,
=22.5?.
k=0 时,
=202.5?.
k=1 时,
x
y
O
22.5?
202.5?
一条终边.
二条终边.
【例题选讲】
例1. 在 0~2p 内, 用角度写出下列各角:
(1)
(2)
(3)
解:
(3)
在 0~2p 内,
=30?.
k=0 时,
=120?.
k=1 时,
=210?.
k=2 时,
=300?.
k=3 时,
x
y
O
30?
120?
210?
300?
一条终边.
二条终边.
四条终边.
发现:
有2n条终边.
例2. 已知 a 是第一象限角, 则 2a 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 上半平面角 (D) 一二象限角
解:
a 是第一象限角,
即
x
y
O
(如图)
4kp
p+4kp
2a
C
将不等式乘以 2 得
例3. 设角 a 的集合为 则
角 a 在坐标平面上有几条不同的终边? 这些终边存
在什么样的关系?
解:
当 k=0 时,
当 k=1 时,
当 k=2 时,
当 k=3 时,
当 k=4 时,
当 k=5 时,
当 k=6 时,
与 k=0 时重合了.
x
y
O
有 6 条不同的终边.
每相邻两条相差60?.
例4. 以原点为端点, 在区间 内任画一
条射线表示角 a 的终边, 则 a 为正角的概率为 .
x
y
O
解:
如图,
在区域
内任作射线是等可能的.
发生 a 为正角的区域为
所求概率为角域的几何概型.
其概率为
练习
补充 第 1、2、3、4、5、6 题.
习题 1.1 A 组 第 9、10 题.
B 组 第 1、2、3 题.
1. 已知角 a 与 b 的终边关于 x 轴对称, a =30?, 则 b = .
2. 已知 a 是锐角, 将 -875? 的角写成 k·180?+a, k?Z 的形式, k = , a = .
3. 已知 a 与 的终边相同, 且 a?(0, 2p), 则 a = .
5. 用弧度制写出终边与直线 x+y=0 重合的角的集合.
6. 已知角 求 a 的终边与圆 x2+y2=1 的交点.
4. 已知 a 是第二象限角, 则 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 第一三象限角 (D) 第二四象限角
1. 已知角 a 与 b 的终边关于 x 轴对称, a =30?, 则 b = .
x
y
O
30?
a
-30?
b
-30?
注意:
习惯性思维: 只看见一个角.
要有 “同终边有很多个角” 的意识.
如图:
+k·360?, k?Z
2. 已知 a 是锐角, 将 -875? 的角写成 k·180?+a , k?Z 的形式, k = , a = .
解:
-875?= -5?180+25?.
-5
25?
3. 已知 a 与 的终边相同, 且 a?(0, 2p), 则 a = .
解:
4. 已知 a 是第二象限角, 则 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 第一三象限角 (D) 第二四象限角
解:
a 是第二象限角,
即
则
x
y
O
当 k=0 时,
当 k=1 时,
(如图)
C
5. 用弧度制写出终边与直线 x+y=0 重合的角的集合.
x
y
O
x+y=0
解:
如图:
直线 x+y=0 与 x 轴交成
45? 的角.
则所求角的集合为
6. 已知角 求 a 的终边与圆 x2+y2=1 的交点.
解:
x
y
O
当 k 取 0, 1, 2, 3 时,
得
得不同的 4 条终边.
A
B
C
D
点 C 与点 A 关于原点对称,
点 D 与点 B 关于原点对称,
9. 要在半径 OA=100 cm 的圆形金属板上截取一块扇形板, 使其弧 AB 的长为 112 cm, 求圆心角∠AOB是多少度 (可用计算器, 精确到1?).
A
B
O
100cm
112cm
解:
圆心角∠AOB的弧度数为
112÷100=1.12,
化成度约为
≈64?,
答: 圆心角∠AOB约等于64度 .
习题 1.1
A 组
10. 已知长 50 cm 的弧为 200?, 求这条弧所在的圆的半径 (可用计算器, 精确到 1 cm).
解:
将200?化为弧度数得
≈14(cm),
答: 这条弧所在的圆的半径 约是14 cm.
B 组
1. 每人准备一把扇子, 然后与本小组其他同学的对比, 从中选出一把展开后看上去形状较为美观的扇子, 并用计算器算出它的面积 S1.
(1) 假设这把扇子是从一个圆面中剪下的, 而剩余部分的面积为 S2, 求 S1 与 S2 的比值;
(2) 要使 S1 与 S2 的比值为 0.618, 则扇子的圆心角应为几度 (精确到10?)?
提示:
(1)
测出扇形半径, 再测出圆心角或弧长,
可用扇形弧在桌面上滚动而测弧长.
B 组
1. 每人准备一把扇子, 然后与本小组其他同学的对比, 从中选出一把展开后看上去形状较为美观的扇子, 并用计算器算出它的面积 S1.
(1) 假设这把扇子是从一个圆面中剪下的, 而剩余部分的面积为 S2, 求 S1 与 S2 的比值;
(2) 要使 S1 与 S2 的比值为 0.618, 则扇子的圆心角应为几度 (精确到10?)?
提示:
(1)
测出扇形半径, 再测出圆心角或弧长,
可用扇形弧在桌面上滚动而测弧长.
(2)
= 0.618,
得 a1≈2.4 rad
≈140?.
12
1
2
3
4
5
6
7
8
9
10
11
2. (1) 时间经过 4 h (时), 时针、分针各转了多少度? 各等于多少弧度?
(2) 有人说, 钟的时针和分针一天内会重合24次,你认为这种说法是否正确? 请说明理由.
解:
(1)
如图,
时针经过4小时所
转的角度为
(-30?)?4= -120?
分针经过 4 小时顺时针转了4 圈,
即转了(-360?)?4 = -1440?
= -8p.
答: 经过4小时时针转了-120?, 等于 弧度;
分针转了-1440?, 等于 -8p 弧度.
12
1
2
3
4
5
6
7
8
9
10
11
2. (1) 时间经过 4 h (时), 时针、分针各转了多少度? 各等于多少弧度?
(2) 有人说, 钟的时针和分针一天内会重合24次,你认为这种说法是否正确? 请说明理由.
解:
(2)
“有人” 说法不正确.
时针与分针重合时, 角度相差 k·360?,
而时针每分钟顺时针转
分针每分钟顺时针转的度数为
=0.5?,
=6?.
设时针与分针经过 t 分钟重合, t≤1440 (24h),
则 6t=0.5t+k·360? (k 为重合次数),
≤1440,
? k≤22,
∴一天内时针与分针只重合22次.
(终边重合)
3. 已知相互啮合的两个齿轮, 大轮有48齿, 小轮有20齿, 当大轮转动一周时, 小轮转动的角是 度,即 rad. 如果大轮的转速为180 r/min (转/分), 小轮的半径为10.5 cm, 那么小轮周上一点每 1 s 转过的弧长是 .
解:
大轮与小轮的齿数比为 12:5.
?a = 864?
864
大轮每秒钟转180?60=3转,
所转过的弧长为
=151.2p (cm).
151.2p cm
则
则小轮每秒钟转
本节完
本节完
人民教育出版社 |必修四
本章内容
1.1 任意角和弧度制
1.2 任意角的三角函数
1.3 三角函数的诱导公式
1.4 三角函数的图象与性质
1.5 函数 y=Asin(wx+j) 的图象
1.6 三角函数模型的简单应用
第一章 小结
1.1.1 任意角(第一课时)
复习与提高
1.1.1 任意角(第二课时)
1.1.2 弧度制
1.1 任意角和弧度制
1.1.1 任意角
(第一课时)
返回目录
1. 什么是正角、负角、零角?
2. 什么是象限角? 什么样的角又不属于象限角?
3. 什么是同终边的角? 怎样找出同终边的角?
学
习
要
点
问题1. 初中我们学过角, 它是由一条射线从起始位置按一定方向绕着端点旋转到终止位置所形成的图形. 当射线绕到起始位置的反向延长线时, 绕过的旋转量是180?, 当射线绕一周到起始位置时, 绕过的旋转量是360?, 请问: 如果绕过两周或三周, 它的旋转量是多少? 如果朝不同方向旋转呢?
【 任意角】
初中我们学了0?~360?
范围的角, 这在实际生活
和科学研究中是远远不够
的.
这一节我们要学习超
出这个范围的角.
O
A
B
180?
360?
1. 正角, 任意大的正角.
规定:
按逆时针方向旋转形成的角叫做正角.
随着终边的旋转, 角可以是 0?~360? 范围内的, 也可以是大于360?的任意大的角.
2. 负角, 任意的负角.
按顺时针方向旋转形成的角叫做负角.
随着终边的顺时针旋转, 角可以是任意的负角.
规定:
1. 正角, 任意大的正角.
规定:
按逆时针方向旋转形成的角叫做正角.
随着终边的旋转, 角可以是 0?~360? 范围内的, 也可以是大于360?的任意大的角.
2. 负角, 任意的负角.
按顺时针方向旋转形成的角叫做负角.
随着终边的顺时针旋转, 角可以是任意的负角.
规定:
角一般用字母 a, b 等希腊字母表示.
在不引起混淆时, 一般省略角符号 “∠”, 简记为 “角a ” 或 “a ”.
3. 零角.
如果一条射线没有作任何旋转, 我们称它形成了零角.
问题2. 零角的终边与始边重合吗 ? 终边与始边重合的角是零角吗 ?
零角的终边与始边重合.
终边与始边重合的角不一定是零角.
终边与始边重合
O
0?
【象限角】
一般地, 我们把角的顶点放在平面直角坐标系的原点, 始边与 x 轴正半轴重合. 如图:
那么, 角的终边在第几象限, 这个角就叫做第几象限的角. 如图:
x
y
o
a =30?,
a是一象限角.
30?
245?
b =245?,
b是三象限角.
g=-270?
g 是 y 轴正
半轴上的角.
d = -200?
d 是
二象限角.
w=-400?
w 是四
象限角.
如果角的终边在坐标轴上, 这个角不属于任何象限. 如图:
练习(补充). 画出下列各角的终边, 并说明是几象限角:
-30? -90? -210? 225? -390? 800?
x
y
-90?
800?
225?
-210?
-390?
-30?
四象限角
y 轴负半轴上的角
二象限角
三象限角
四象限角
一象限角
【同终边的角】
问题3. 30?角和390?角始边相同的时候, 终边是否重合? 30?角和-30?角始边相同的时候, 终边是否重合? 你能说出几个与-30?角始边相同, 且终边重合的角吗?
始边
终边
O
30?
-30?
终边
390?
始边相同时,
30?与390?的终边相同,
30?与-30?的终边不相同.
设角 a 是 0?~360?之间的角时, 与 a 同终边的角写成
k·360?+a, k?Z.
例1. 在 0?~360? 范围内, 找出与 -950?12? 角终边相同的角, 并判定它是第几象限角.
分析:
-950?12? 是顺时针旋转两周又230?12?,
x
y
O
也可顺时针旋转三周又
逆时针旋转129?48?.
-360?
-720?
-230?12?
-1080?
129?48?
∴在 0?~360? 范围内与
-950?12? 同终边的角是 129?48?.
即 -950?12?= -2?360?-230?12?.
-950?12?与 -230?12? 同终边.
即 -950?12?= -3?360?+129?48?.
-950?12?与 129?48? 同终边.
-1080?
例1. 在 0?~360? 范围内, 找出与 -950?12? 角终边相同的角, 并判定它是第几象限角.
x
y
O
129?48?
任一个角 b 都可以写成
k·360?+a 的形式,
k?Z, a 是 0?~360? 间的角.
即 b = k·360?+a, 其中
则 b 与 a 同终边.
(补充). 在 0?~360? 范围内, 找出与下列各角终边相同的角, 并指出它们是第几角象限角:
(1) -750?; (2) 1000?28?.
练习(课本5页)
第 1、2 题
练习: (课本5页)
1. (口答) 锐角是第几象限角? 第一象限角一定是锐角吗? 再分别就直角、钝角来回答这两个问题.
锐角是第一象限角.
第一象限角不一定是锐角.
直角终边与 y 轴非负半轴重合, 不属任何象限角.
钝角是第二象限角, 但第二象限角不一定是钝角.
2. (口答) 今天是星期三, 那么7k (k?Z)天后的那一天是星期几? 7k (k?Z)天前的那一天是星期几? 100天后的那一天是星期几?
今天是星期三, 那么7k (k?Z)天后的那一天
星期是以7天为周期循环出现的.
也是星期三,
7k (k?Z)天前的那一天也是星期三.
100=14?7+2,
∴ 100天后的那一天是星期五.
(补充). 在 0?~360? 范围内, 找出与下列各角终边相同的角, 并指出它们是第几角象限角:
(1) -750?; (2) 1000?28?.
解:
(1)
∵-750?= 3?(-360?)+330?,
∴在 0?~360? 范围内与角-750?终边相同的角是
330?,
(2)
∵1000?28?= 2?360?+279?32?,
∴在 0?~360? 范围内与角1000?28?终边相同的角
是 279?32?,
它是第四象限角.
它是第四象限角.
【课时小结】
1. 正角、负角、零角
按逆时针方向旋转形成的角叫做正角.
旋转一周后大于360?, 旋转两周后大于720?.
按顺时针方向旋转形成的角叫做负角.
旋转一周后小于-360?, 旋转两周后小于-720?.
一条射线不作任何旋转, 与它自己形成 0? 的角.
零角的终边与始边重合.
终边与始边重合的角不一定是零角.
【课时小结】
2. 象限角
终边在第几象限, 就叫做第几象限的角.
终边在坐标轴上, 不属于任何象限角.
锐角是一象限角.
一象限角不一定是锐角.
钝角是二象限角.
二象限角不一定是钝角.
【课时小结】
3. 同终边的角
始边相同, 终边重合的角.
a 是 0?~360? 内的角, 与 a 同终边的角为
k·360?+a, k?Z.
第 3、4 题.
练习: (课本5页)
3. 已知角的顶点与直角坐标系的原点重合, 始边与 x 轴的非负半轴重合, 作出下列各角, 并指出它们是第几象限的角:
(1) 420?; (2) -75?; (3) 855?; (4) -510?.
x
y
o
420?
855?
-75?
-510?
解:
(1)
420? 是第一象限角.
(2)
-75? 是第四象限角.
(3)
855? 是第二象限角.
(4)
-510? 是第三象限角.
4. 在 0?~360? 范围内, 找出与下列各角终边相同的角, 并指出它们是第几角象限角:
(1) -54?18?; (2) 395?8?; (3) -1190?30?.
解:
(1)
∵-54?18?= -360?+305?42?,
∴在 0?~360? 范围内与角-54?18?终边相同的角是
305?42?,
(2)
∵395?8?= 360?+35?8?,
∴在 0?~360? 范围内与角395?8?终边相同的角是
35?8?,
它是第四象限角.
它是第一象限角.
(3)
∵-1190?30?= -360??4+249?30?,
∴在 0?~360? 范围内与角-1190?30?终边相同的角
是249?30?,
它是第三象限角.
1.1.1 任意角
(第二课时)
返回目录
1. 与一个角 a 同终边的角的集合怎样表示?
2. 终边在 x 轴上的角怎样表示? 终边在 y 轴上的角怎样表示?
3. 终边在某一象限的角怎样表示? 终边在某一范围内的角怎样表示?
学
习
要
点
问题1. 已知角a =30?, 与a 同终边的角还有哪些? 这些角的集合怎样表示?
x
y
o
a =30?
正角:
30?+360?,
30?+2?360?,
30?+3?360?, …
如图,
【同终边的角的集合】
问题1. 已知角a =30?, 与a 同终边的角还有哪些? 这些角的集合怎样表示?
x
y
o
正角:
各角与a 都相差整数个360?.
所有与a 同终边的角, 连同a 在内, 可构成一个集合:
S={ b | b =a + k·360?, k∈Z }.
30?+360?,
30?+2?360?,
30?+3?360?, …
30?-360?,
30?-2?360?,
30?-3?360?, …
负角:
如图,
【同终边的角的集合】
a =30?
例(补充). 已知a 为锐角, 且sina = 画出a 的终边, 并写出与a 同终边的角的集合.
解:
锐角a =45?,
a 的终边与第一象限的
角平分线重合 (如图),
x
y
o
a
与a 同终边的角的集合为
{ b |b =45?+ k?360?, k?Z }.
例2. 写出终边在 y 轴上的角的集合.
解:
在 0?~360? 范围内, 终边在 y 轴上的角有两个,
即 90? 和 270?.
与90?同终边的角的集集合为
S1={b |b =90?+k·360?, k?Z};
与270?同终边的角的集集合为
S2={b |b =270?+k·360?, k?Z}.
合并 S1 与 S2 为:
x
y
o
90?
270?
180?
180?
两条终边构成一个平角,
它们相差 k 个180?,
S = S1∪S2
={b |b = 90?+n·180?, n?Z}.
例3. 写出终边在直线 y = x 上的角的集合 S, 并把 S 中适合不等式-360?≤b <720? 的元素b 写出来.
解:
x
y
o
因为直线 y=x 是第一、
三象限的角平分线,
在 0?~360?
范围内有45?和225?两个角,
45?
225?
这两个角相差 k 个180?,
∴与这两个角同终边的
角的集合为
S = { b | b = 45?+k·180?, k?Z }.
取 k = -2, -1, 0, 1, 2, 3 ,
b 的值分别为
-315?,
45?,
225?,
405?,
585?.
-135?,
要使-360?≤b <720?,
【互为反向延长线的两条终边的角的集合】
x
y
o
a
S = { b | b = a +
{ b | b = a +
∪
= { b | b = a + n?180?, n∈Z }.
k?360?, k∈Z }
180?+k?360?, k∈Z }
与两条互为反向延长线的终边重合的所有角的集合的写法:
={b | b =a+2k?180?, k?Z }
∪{b | b =a+(2k+1)?180?, k?Z}
练习: (补充)
1. 写出终边与 x 轴正、负半轴重合的角的集合.
练习: (课本5页)
5. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-720?≤b <360?的元素 b 写出来:
(1) 1303?18?; (2) -225?.
1. 写出终边与 x 轴正、负半轴重合的角的集合.
x
y
o
解:
终边与 x 轴正半轴重合的是
k?360?,
与 x 轴负半轴重合的是
∴ 终边与 x 轴正、负半轴
S={ b | b = k?180? , k∈Z }.
k?360?+180?,
重合的所有角的集合为
练习: (补充)
练习: (课本5页)
5. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-720?≤b <360?的元素 b 写出来:
(1) 1303?18?; (2) -225?.
解:
S={ b | b = 1303?18?+k·360?, k∈Z },
∴取 k = -5, -4, -3,
-496?42?,
(1)
∵ -720?≤b <360?,
集合中满足条件的元素 b 分别为
-136?42?,
223?18?.
练习: (课本5页)
5. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-720?≤b <360?的元素 b 写出来:
(1) 1303?18?; (2) -225?.
解:
S={ b | b = -225?+k·360?, k∈Z },
∴取 k = -1, 0, 1,
-585?,
(2)
∵ -720?≤b <360?,
集合中满足条件的元素 b 分别为
-225?,
135?.
【终边在某范围内的角的集合】
问题2. 终边与0?~60?间的角重合的角的集合怎样表示? 终边在第二象限的角的集合怎样表示?
< b <
x
y
o
0?
60?
起始位置
终止位置
k·360?
60?+k·360?,
k∈Z }.
{ b |
x
y
o
90?
180?
起始位置
终止位置
90?+k·360?,
180?+k·360?,
集合: { b |90?+k·360?b
b
终边在第二象限:
例 (补充). 已知集合 S={ b | k·360?-45?
① 画出 k·360?- 45?的终边,
③ 按逆时针从终边①到
终边②之间的区域就
是角 b 的终边的范围.
如图:
x
y
o
② 画出k·360?+150?的终边,
①
②
k·360?-45?
k·360?+150?
练习(补充). 若 a 是第二象限的角, 则 2a 是第几象限的角? 是第几象限的角?
x
y
o
解:
如图,
用不等式表示a 的范围:
90?+k?360?360?+2k?360?, k∈Z, (如图)
<2a <
180?+2k?360?
180?+k?360?
360?+2k?360?
∴ 2a 是三、四象限及 y 轴负半轴上的角,
即下半平面的角.
45?+k?180?
90?+k?180?, k∈Z,
45?+k?180?
45?+k?180?
90?+k?180?
90?+k?360?
∴ 是一、三象限的角.
180?+2k?360?
90?+k?180?
k∈Z,
计算 2a 的范围:
计算 的范围:
【课时小结】
1. 与角 a 同终边的角的集合
S={ b | b =a + k·360?, k∈Z }.
2. 与角 a 以及 a+180? 同终边的角的集合
{ b | b = a + n?180?, n∈Z }.
与 x 轴重合的终边有两条, 角的集合为
{ b | b = k?180?, k∈Z }.
与 y 轴重合的终边也有两条, 角的集合为
{ b | b = 90?+k?180?, k∈Z }.
【课时小结】
3. 某范围内的角的集合
{g |a+k·360?< g
y
O
a
b
g
第一象限角的集合
{g |k·360?< g <90?+k·360?, k?Z}.
终边在右半平面内角的集合
{g |-90?+k·360?< g <90?+k·360?, k?Z}.
习题 1.1
A 组
第 1、2、3、5 题.
1. 在0?~360?范围内,找出与下列各角终边相同的角, 并指出它们是哪个象限的角:
(1) -265?; (2) -1000?; (3) -843?10?; (4) 3900?.
解:
(1)
∵-265? = -360?+95?,
∴在0?~360?范围内与-265?终边相同的角是95?.
(2)
∵-1000? = -3?360?+80?,
∴在0?~360?范围内与-1000?终边相同的角是80?.
它们是第二象限的角.
它们是第一象限的角.
习题 1.1
A 组
1. 在0?~360?范围内,找出与下列各角终边相同的角, 并指出它们是哪个象限的角:
(1) -265?; (2) -1000?; (3) -843?10?; (4) 3900?.
解:
(3)
∵-843?10? = -3?360?+236?50?,
∴在0?~360?范围内与-843?10?终边相同的角是236?50?.
(4)
∵3900? = 10?360?+300?,
∴在0?~360?范围内与3900?终边相同的角是300?.
它们是第三象限的角.
它们是第四象限的角.
习题 1.1
A 组
2. 写出终边在 x 轴上的角的集合.
解:
终边在 x 轴上包括正半轴方向和负半轴方向,
这些角与 0? 角相差整数个 180?.
所以终边在 x 轴上的角的集合为
S={b | b = n·180?, n?Z}.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(1)
S={ b | b = 60?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -1, 0,
得满足条件的元素 b 为
-300?,
60?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(2)
S={ b | b = -75?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = 0, 1,
得满足条件的元素 b 为
-75?,
285?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(3)
S={ b | b = - 824?30?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = 2, 3,
得满足条件的元素 b 为
-104?30?,
255?30?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(4)
S={ b | b = 475?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -2, -1,
得满足条件的元素 b 为
-245?,
115?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(5)
S={ b | b = 90?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -1, 0,
得满足条件的元素 b 为
-270?,
90?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(6)
S={ b | b = 270?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -1, 0,
得满足条件的元素 b 为
-90?,
270?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(7)
S={ b | b = 180?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -1, 0,
得满足条件的元素 b 为
-180?,
180?.
3. 写出与下列各角终边相同的角的集合, 并把集合中适合不等式-360?≤b <360?的元素 b 写出来:
(1) 60?; (2) -75?; (3) -824?30?; (4) 475?;
(5) 90?; (6) 270?; (7) 180?; (8) 0?.
解:
(8)
S={ b | b = 0?+k·360?, k∈Z },
∵-360?≤b <360?,
∴取 k = -1, 0,
得满足条件的元素 b 为
-360?,
0?.
5. 选择题:
(1) 已知 a 是锐角, 那么 2a 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 小于180?的正角 (D) 第一或第二象限角
(2) 已知 a 是第一象限角, 那么 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 第一或第二象限角 (D) 第一或第三象限角
解:
(1)
∵ a 是锐角,
则 0?∴ 0?<2a <180?,
则应选C.
C
5. 选择题:
(1) 已知 a 是锐角, 那么 2a 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 小于180?的正角 (D) 第一或第二象限角
(2) 已知 a 是第一象限角, 那么 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 第一或第二象限角 (D) 第一或第三象限角
解:
(2)
∵ a 是第一象限角,
则 k·360?则应选D.
C
x
y
o
45?
45?
k·180?
k·180?
45?+k·180?
45?+k·180?
得
D
1.1.2
弧度制
返回目录
1. 什么是弧度制? 扇形中的弧长、半径、圆心角的弧度数是怎样的关系?
2. 弧度制与角度制怎样换算?
3. 特殊角的弧度数有什么规律? 你能熟练掌握特殊角的弧度数吗?
学
习
要
点
问题1: 请同学们画一个扇形, 使它的弧长等于半径, 你估计这个扇形的圆心角是多少? 这个圆心角是周角的几分之几?
=1弧度
r
l
a
扇形所在圆的周长为
2p r,
那么圆心角 a 是周角的
即
我们把弧长等于半径的圆心角叫做 1 弧度的角.
用 rad 表示, 读作弧度.
l = r
弧长是周长的
≈57?18?.
=1 rad.
在角度制中, 周角的 是 1 度的角.
在弧度制中, 周角的 是 1 弧度的角.
问题2. 1 周角有多少弧度? 1 弧度有多少度?
1 周角=2p 弧度.
1 弧度≈57?18?.
360?=2p rad,
180?=p rad,
※一般地, 正角的弧度数是一个正数, 负角的弧度数是一个负数, 零角的弧度数是 0. 如果半径为 r 的圆的圆心角 a 所对的弧长为 l, 那么, 角 a 的弧度数的绝对值是
例1. 按照下列要求, 把67?30?化成弧度:
(1) 精确值;
(2) 精确到0.001的近似值.
解:
(1)
∴ 67?30? = 67.5?
(2)
≈1.178 rad.
例2. 将 3.14 rad 换算成角度 (用度数表示, 精确到 0.001).
解:
=179.922?.
今后用弧度制表示角度时, “弧度” 二字或 “rad”通常略去不写, 而只写该角所对应的弧度数.
如角 a =2 表示 a 是 2 rad 的角,
角 表示 b 是 弧度的角.
∵1rad≈57.3?,
∴3.14rad≈57.3??3.14
请填写下表中特殊角的弧度数:
度
0?
30?
45?
60?
90?
120?
135?
150?
180?
270?
360?
弧度
在实际应用中, 常用多少p 弧度表示弧度的精确值.
请记住这些特殊角的弧度数.
0
对于一些特殊角的弧度数要经常用到.
例(补充). 用弧度数表示下列角的集合:
(1) 终边与90?角的终边重合;
(2) 终边与直线 y = x 重合.
解:
(1)
∴ 用弧度制表示终边与90?重合的角的集合为
(2)
∵ 终边与直线 y = x 重合的角的集合为
x
y
o
例4. 利用计算器比较 sin1.5 和 sin85? 的大小.
解:
用计算器求得 sin1.5 ≈0.9974,
sin85?≈0.9962,
∴sin1.5 > sin85?.
练习: (课本9页)
第 1、2 题.
1. 把下列角度化成弧度:
(1) 22?30?; (2) -210?; (3) 1200?.
解:
(1)
∴ 22?30?=22.5?
(2)
(3)
练习: (课本9页)
2. 把下列弧度化成度:
(1) (2) (3)
解:
(1)
=15?.
(2)
= -240?.
(3)
= 54?.
例3. 利用弧度制证明下列关于扇形的公式:
(1) l =a R; (2) (3)
证明:
(1)
∴ l = |a|R,
又a > 0,
∴ l = a R.
(2)
(3)
l
R
(变态三解形)
∵1 弧度是周角的
∴ 1 弧度的扇形面积是圆面积的
则 a 弧度的扇形面积为
l = a R.
R: 半径, l : 弧长, S: 面积,
a : 圆心角的弧度数,
在扇形中,
练习(补充). 已知半径为120 mm的圆上, 有一条弧的长是144 mm, 求此弧所对的圆心角的弧度数, 以及所对扇形的面积.
解:
答: 圆心角是1.2 rad, 扇形的面积是8640 mm2.
【课时小结】
1. 弧度制
用弧度表示角的大小.
弧长等于半径的圆心角叫做 1 弧度的角.
=1弧度
r
l
a
l = r
【课时小结】
2. 弧度与角度的换算
1 周角=2p 弧度.
1 平角=p 弧度.
【课时小结】
3. 特殊角的弧度数
弧度
360?
270?
180?
150?
135?
120?
90?
60?
45?
30?
0?
度
0
【课时小结】
4. 用弧度数表示扇形的弧长与面积
l = a R.
R: 半径, l : 弧长, S: 面积,
a : 圆心角的弧度数,
练习: (课本9页)
第 3、4、5、6 题.
习题 1.1
A 组
第 4、 6、7、8 题.
3. 用弧度表示:
(1) 终边在 x 轴上的集合;
(2) 终边在 y 轴上的集合.
解:
(1)
终边在 x 轴上的集合为:
S={a |a = kp, k?Z}.
(2)
终边在 y 轴上的集合为:
练习: (课本9页)
4. 利用计算器比较下列各对值的大小 (精确到0.001):
(1) cos0.75? 和 cos0.75; (2) tan1.2? 和 tan1.2.
解:
(1)
∵cos0.75?≈1.000,
cos0.75≈0.732,
∴cos0.75?>cos0.75.
(2)
∵tan1.2?≈0.021,
tan1.2≈2.572,
∴tan1.2?
解:
角度制:
弧度制:
≈1.047(m);
∴ l=aR
≈1.05(m).
6. 已知半径为120 mm 的圆上, 有一条弧的长是144 mm, 求该弧所对的圆心角的弧度数.
解:
又 l =144 mm, R=120 mm,
=1.2 (rad).
习题 1.1
A 组
4. 分别用角度和弧度写出第一、二、三、四象限角的集合.
解:
角度表示:
弧度表示:
第一象限角:
第二象限角:
{b |k·360?角度表示:
弧度表示:
{b |90?+k·360?习题 1.1
A 组
4. 分别用角度和弧度写出第一、二、三、四象限角的集合.
解:
角度表示:
弧度表示:
第三象限角:
第四象限角:
角度表示:
弧度表示:
{b |270?+k·360?{b |180?+k·360? 6. 一条弦的长等于半径, 这条弦所对的圆心角等于 1 弧度吗? 为什么?
答: 不等于 1 弧度.
当且仅当 l=r 时, 圆心角
r
l
d
(如图)
才是 1 弧度的角.
而 d=r, l>d,
则 l>r.
∴圆心角不是 1 弧度的角.
7. 把下列各角度化成弧度:
(1) 36?; (2) -150?; (3) 1095?; (4) 1440?.
解:
(1)
(2)
(3)
(4)
= 8p rad.
8. 把下列各弧度化成度:
(1) (2) (3) 1.4; (4)
解:
(1)
= -210?.
(2)
= -600?.
(3)
≈80?12?.
(4)
≈38?12?.
复习与提高
复习与提高
返回目录
1. 任意角
正角、负角、零角
2. 象限角
终边在第几象限, 就叫做第几象限的角.
终边在坐标轴上, 不属于任何象限角.
3. 同终边的角
始边相同, 终边重合的角.
与 a 同终边的角的集合
{b |b =a+k·360?, k?Z}.
与 a 和 a 的反向延长线同终边的角的集合
{b |b =a+k·180?, k?Z}.
知识要点
4. 和某范围内终边相同的角的集合
{g |a+k·360?< g
y
O
a
b
g
终边在上半平面的角的集合
{g |k·360?< g <180?+k·360?, k?Z}.
终边在右半平面内角的集合
{g |-90?+k·360?< g <90?+k·360?, k?Z}.
知识要点
5. 弧度制
弧长等于半径的圆心角叫做 1 弧度的角.
=1弧度
r
l
a
l = r
6. 弧度与角度的换算
1 周角=2p 弧度.
1 平角=p 弧度.
知识要点
7. 用弧度数表示扇形的弧长与面积
l = a R.
R: 半径, l : 弧长, S: 面积,
a : 圆心角的弧度数,
知识要点
【例题选讲】
例1. 在 0~2p 内, 用角度写出下列各角:
(1)
(2)
(3)
解:
(1)
在 0~2p 内, 取 k=0 时,
=15?.
x
y
O
15?
一条终边.
【例题选讲】
例1. 在 0~2p 内, 用角度写出下列各角:
(1)
(2)
(3)
解:
(2)
在 0~2p 内,
=22.5?.
k=0 时,
=202.5?.
k=1 时,
x
y
O
22.5?
202.5?
一条终边.
二条终边.
【例题选讲】
例1. 在 0~2p 内, 用角度写出下列各角:
(1)
(2)
(3)
解:
(3)
在 0~2p 内,
=30?.
k=0 时,
=120?.
k=1 时,
=210?.
k=2 时,
=300?.
k=3 时,
x
y
O
30?
120?
210?
300?
一条终边.
二条终边.
四条终边.
发现:
有2n条终边.
例2. 已知 a 是第一象限角, 则 2a 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 上半平面角 (D) 一二象限角
解:
a 是第一象限角,
即
x
y
O
(如图)
4kp
p+4kp
2a
C
将不等式乘以 2 得
例3. 设角 a 的集合为 则
角 a 在坐标平面上有几条不同的终边? 这些终边存
在什么样的关系?
解:
当 k=0 时,
当 k=1 时,
当 k=2 时,
当 k=3 时,
当 k=4 时,
当 k=5 时,
当 k=6 时,
与 k=0 时重合了.
x
y
O
有 6 条不同的终边.
每相邻两条相差60?.
例4. 以原点为端点, 在区间 内任画一
条射线表示角 a 的终边, 则 a 为正角的概率为 .
x
y
O
解:
如图,
在区域
内任作射线是等可能的.
发生 a 为正角的区域为
所求概率为角域的几何概型.
其概率为
练习
补充 第 1、2、3、4、5、6 题.
习题 1.1 A 组 第 9、10 题.
B 组 第 1、2、3 题.
1. 已知角 a 与 b 的终边关于 x 轴对称, a =30?, 则 b = .
2. 已知 a 是锐角, 将 -875? 的角写成 k·180?+a, k?Z 的形式, k = , a = .
3. 已知 a 与 的终边相同, 且 a?(0, 2p), 则 a = .
5. 用弧度制写出终边与直线 x+y=0 重合的角的集合.
6. 已知角 求 a 的终边与圆 x2+y2=1 的交点.
4. 已知 a 是第二象限角, 则 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 第一三象限角 (D) 第二四象限角
1. 已知角 a 与 b 的终边关于 x 轴对称, a =30?, 则 b = .
x
y
O
30?
a
-30?
b
-30?
注意:
习惯性思维: 只看见一个角.
要有 “同终边有很多个角” 的意识.
如图:
+k·360?, k?Z
2. 已知 a 是锐角, 将 -875? 的角写成 k·180?+a , k?Z 的形式, k = , a = .
解:
-875?= -5?180+25?.
-5
25?
3. 已知 a 与 的终边相同, 且 a?(0, 2p), 则 a = .
解:
4. 已知 a 是第二象限角, 则 是 ( )
(A) 第一象限角 (B) 第二象限角
(C) 第一三象限角 (D) 第二四象限角
解:
a 是第二象限角,
即
则
x
y
O
当 k=0 时,
当 k=1 时,
(如图)
C
5. 用弧度制写出终边与直线 x+y=0 重合的角的集合.
x
y
O
x+y=0
解:
如图:
直线 x+y=0 与 x 轴交成
45? 的角.
则所求角的集合为
6. 已知角 求 a 的终边与圆 x2+y2=1 的交点.
解:
x
y
O
当 k 取 0, 1, 2, 3 时,
得
得不同的 4 条终边.
A
B
C
D
点 C 与点 A 关于原点对称,
点 D 与点 B 关于原点对称,
9. 要在半径 OA=100 cm 的圆形金属板上截取一块扇形板, 使其弧 AB 的长为 112 cm, 求圆心角∠AOB是多少度 (可用计算器, 精确到1?).
A
B
O
100cm
112cm
解:
圆心角∠AOB的弧度数为
112÷100=1.12,
化成度约为
≈64?,
答: 圆心角∠AOB约等于64度 .
习题 1.1
A 组
10. 已知长 50 cm 的弧为 200?, 求这条弧所在的圆的半径 (可用计算器, 精确到 1 cm).
解:
将200?化为弧度数得
≈14(cm),
答: 这条弧所在的圆的半径 约是14 cm.
B 组
1. 每人准备一把扇子, 然后与本小组其他同学的对比, 从中选出一把展开后看上去形状较为美观的扇子, 并用计算器算出它的面积 S1.
(1) 假设这把扇子是从一个圆面中剪下的, 而剩余部分的面积为 S2, 求 S1 与 S2 的比值;
(2) 要使 S1 与 S2 的比值为 0.618, 则扇子的圆心角应为几度 (精确到10?)?
提示:
(1)
测出扇形半径, 再测出圆心角或弧长,
可用扇形弧在桌面上滚动而测弧长.
B 组
1. 每人准备一把扇子, 然后与本小组其他同学的对比, 从中选出一把展开后看上去形状较为美观的扇子, 并用计算器算出它的面积 S1.
(1) 假设这把扇子是从一个圆面中剪下的, 而剩余部分的面积为 S2, 求 S1 与 S2 的比值;
(2) 要使 S1 与 S2 的比值为 0.618, 则扇子的圆心角应为几度 (精确到10?)?
提示:
(1)
测出扇形半径, 再测出圆心角或弧长,
可用扇形弧在桌面上滚动而测弧长.
(2)
= 0.618,
得 a1≈2.4 rad
≈140?.
12
1
2
3
4
5
6
7
8
9
10
11
2. (1) 时间经过 4 h (时), 时针、分针各转了多少度? 各等于多少弧度?
(2) 有人说, 钟的时针和分针一天内会重合24次,你认为这种说法是否正确? 请说明理由.
解:
(1)
如图,
时针经过4小时所
转的角度为
(-30?)?4= -120?
分针经过 4 小时顺时针转了4 圈,
即转了(-360?)?4 = -1440?
= -8p.
答: 经过4小时时针转了-120?, 等于 弧度;
分针转了-1440?, 等于 -8p 弧度.
12
1
2
3
4
5
6
7
8
9
10
11
2. (1) 时间经过 4 h (时), 时针、分针各转了多少度? 各等于多少弧度?
(2) 有人说, 钟的时针和分针一天内会重合24次,你认为这种说法是否正确? 请说明理由.
解:
(2)
“有人” 说法不正确.
时针与分针重合时, 角度相差 k·360?,
而时针每分钟顺时针转
分针每分钟顺时针转的度数为
=0.5?,
=6?.
设时针与分针经过 t 分钟重合, t≤1440 (24h),
则 6t=0.5t+k·360? (k 为重合次数),
≤1440,
? k≤22,
∴一天内时针与分针只重合22次.
(终边重合)
3. 已知相互啮合的两个齿轮, 大轮有48齿, 小轮有20齿, 当大轮转动一周时, 小轮转动的角是 度,即 rad. 如果大轮的转速为180 r/min (转/分), 小轮的半径为10.5 cm, 那么小轮周上一点每 1 s 转过的弧长是 .
解:
大轮与小轮的齿数比为 12:5.
?a = 864?
864
大轮每秒钟转180?60=3转,
所转过的弧长为
=151.2p (cm).
151.2p cm
则
则小轮每秒钟转
本节完
本节完
