2.5.1直线与圆的位置关系(课堂检测+素养作业) 2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册Word含解析
文档属性
| 名称 | 2.5.1直线与圆的位置关系(课堂检测+素养作业) 2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册Word含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 292.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览




文档简介
2.5.1直线与圆的位置关系
1.直线3x+4y-5=0与圆x2+y2=1的位置关系是( )
A.相交 B.相切
C.相离 D.无法判断
2.若直线l与圆C有公共点,则直线l与圆C的位置关系是( )
A.相交 B.相切
C.相离 D.相切或相交
3.直线x+2y-5+=0被圆x2+y2-2x-4y=0截得的弦长为( )
A.1 B.2
C.4 D.4
4.(全国卷Ⅰ,文)设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A、B两点,若|AB|=2,则圆C的面积为__ __.
5.已知圆C:x2+y2-4x+3=0,过原点的直线l与其交于不同的两点A、B.
(1)求直线l的斜率k的取值范围;
(2)求线段AB的中点P的轨迹方程.
A组·素养自测
一、选择题
1.(2021·北京市海淀区检测)直线3x+4y-13=0与圆(x-2)2+(y-3)2=1的位置关系是( )
A.相离 B.相交
C.相切 D.无法判定
2.已知直线ax+by+c=0(a、b、c都是正数)与圆x2+y2=1相切,则以a、b、c为三边长的三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不存在
3.(2020·九江一中高一期末)已知圆C:x2+y2=9,点P为直线x+2y-9=0上一动点,过点P向圆C引两条切线PA、PB,且A、B为切点,则直线AB经过定点( )
A.(4,8) B.(2,4)
C.(1,2) D.(9,0)
4.(2020·四川省南充市三模)已知圆的方程为x2+y2=1,则经过圆上一点M(1,0)的切线方程是( )
A.x=1 B.y=1
C.x+y=1 D.x-y=1
5.(2020·临朐一中高一检测)若圆心坐标为(2,-1)的圆在直线x-y-1=0上截得的弦长为2,则这个圆的方程是( )
A.(x-2)2+(y+1)2=2 B.(x-2)2+(y+1)2=4
C.(x-2)2+(y+1)2=8 D.(x-2)2+(y+1)2=16
二、填空题
6.圆(x-3)2+(y-3)2=9上到直线3x+4y-11=0的距离等于1的点有____个.
7.(天津文)已知圆C的圆心在x轴的正半轴上,点M(0,)在圆C上,且圆心到直线2x-y=0的距离为,则圆C的方程为____.
8.(2020·河北省石家庄市正定三中高二期中)已知圆C与直线x-6y-10=0相切于点(4,-1),且经过点(9,6),则圆C的方程为____.
三、解答题
9.求满足下列条件的圆x2+y2=4的切线方程:
(1)经过点P(,1);
(2)斜率为-1;
(3)过点Q(3,0).
10.(2020·本溪一中高一期中)已知点M(3,1),直线ax-y+4=0及圆(x-1)2+(y-2)2=4.
(1)求过点M的圆的切线方程;
(2)若直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2,求a的值.
B组·素养提升
一、选择题
1.(多选题)平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是( )
A.2x+y+5=0 B.2x+y-5=0
C.2x+y+=0 D.2x+y-=0
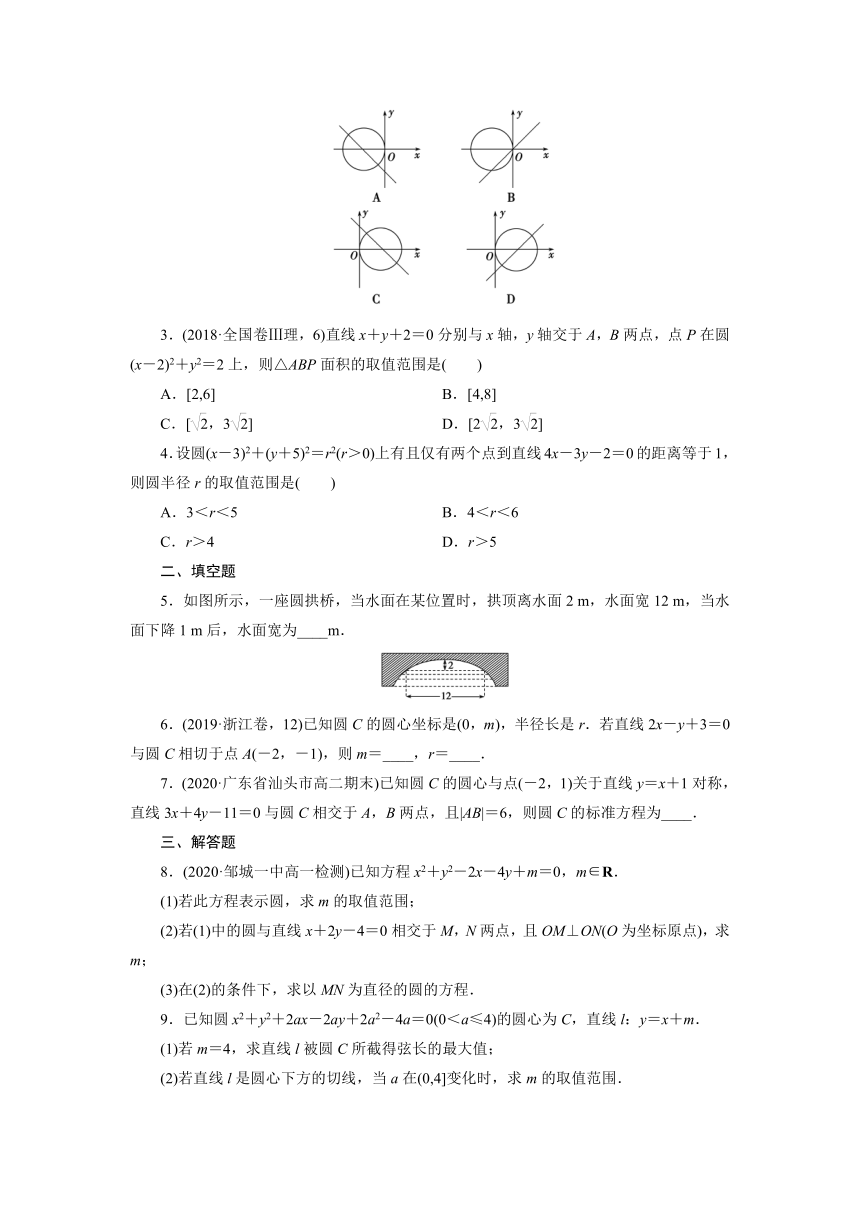
2.(多选题)在同一直角坐标系中,直线y=ax+a2与圆(x+a)2+y2=a2的位置不可能为( )
3.(2018·全国卷Ⅲ理,6)直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x-2)2+y2=2上,则△ABP面积的取值范围是( )
A.[2,6] B.[4,8]
C.[,3] D.[2,3]
4.设圆(x-3)2+(y+5)2=r2(r>0)上有且仅有两个点到直线4x-3y-2=0的距离等于1,则圆半径r的取值范围是( )
A.3<r<5 B.4<r<6
C.r>4 D.r>5
二、填空题
5.如图所示,一座圆拱桥,当水面在某位置时,拱顶离水面2 m,水面宽12 m,当水面下降1 m后,水面宽为____m.
6.(2019·浙江卷,12)已知圆C的圆心坐标是(0,m),半径长是r.若直线2x-y+3=0与圆C相切于点A(-2,-1),则m=____,r=____.
7.(2020·广东省汕头市高二期末)已知圆C的圆心与点(-2,1)关于直线y=x+1对称,直线3x+4y-11=0与圆C相交于A,B两点,且|AB|=6,则圆C的标准方程为____.
三、解答题
8.(2020·邹城一中高一检测)已知方程x2+y2-2x-4y+m=0,m∈R.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且OM⊥ON(O为坐标原点),求m;
(3)在(2)的条件下,求以MN为直径的圆的方程.
9.已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.
(1)若m=4,求直线l被圆C所截得弦长的最大值;
(2)若直线l是圆心下方的切线,当a在(0,4]变化时,求m的取值范围.
2.5.1直线与圆的位置关系
1.直线3x+4y-5=0与圆x2+y2=1的位置关系是( B )
A.相交 B.相切
C.相离 D.无法判断
[解析] d==1=r,∴选B.
2.若直线l与圆C有公共点,则直线l与圆C的位置关系是( D )
A.相交 B.相切
C.相离 D.相切或相交
[解析] 当只有一个公共点时,直线l与圆C相切;当有两个公共点时,直线l与圆C相交.
3.直线x+2y-5+=0被圆x2+y2-2x-4y=0截得的弦长为( C )
A.1 B.2
C.4 D.4
[解析] 依题意,圆的圆心为(1,2),半径r=,圆心到直线的距离d==1,所以结合图形可知弦长的一半为=2,故弦长为4.
4.(全国卷Ⅰ,文)设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A、B两点,若|AB|=2,则圆C的面积为__4π__.
[解析] 圆C的方程可化为x2+(y-a)2=a2+2,可得圆心的坐标为C(0,a),半径r=,所以圆心到直线x-y+2a=0的距离为=,所以()2+()2=()2,解得a2=2,所以圆C的半径为2,所以圆C的面积为4π.
5.已知圆C:x2+y2-4x+3=0,过原点的直线l与其交于不同的两点A、B.
(1)求直线l的斜率k的取值范围;
(2)求线段AB的中点P的轨迹方程.
[解析] (1)圆C的标准方程为(x-2)2+y2=1,
由题意可设直线l的方程为y=kx.
∵直线l与圆C有两个不同交点,
∴<1,
∴-<k<.
(2)设点P(x,y),∵点P为线段AB的中点,∴CP⊥OP.
∴kCP·kOP=-1,
即·=-1(x≠2且x≠0),
化简得x2+y2-2x=0.
由得
故点P的轨迹方程为x2+y2-2x=0(<x≤2).
A组·素养自测
一、选择题
1.(2021·北京市海淀区检测)直线3x+4y-13=0与圆(x-2)2+(y-3)2=1的位置关系是( C )
A.相离 B.相交
C.相切 D.无法判定
[解析] 由圆的方程可知,圆心坐标为(2,3),半径r=1,所以圆心到直线3x+4y-13=0的距离d==1=r,则直线与圆的位置关系为相切.
2.已知直线ax+by+c=0(a、b、c都是正数)与圆x2+y2=1相切,则以a、b、c为三边长的三角形是( B )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不存在
[解析] 由题意,得=1,
∴a2+b2=c2,故选B.
3.(2020·九江一中高一期末)已知圆C:x2+y2=9,点P为直线x+2y-9=0上一动点,过点P向圆C引两条切线PA、PB,且A、B为切点,则直线AB经过定点( C )
A.(4,8) B.(2,4)
C.(1,2) D.(9,0)
[解析] 设P(9-2b,b),由圆的切线公式,则直线lAB:(9-2b)x+by=9,即b(y-2x)+9x=9,
所以定点?.
4.(2020·四川省南充市三模)已知圆的方程为x2+y2=1,则经过圆上一点M(1,0)的切线方程是( A )
A.x=1 B.y=1
C.x+y=1 D.x-y=1
[解析] 方法一 由圆的方程为x2+y2=1,可知圆心的坐标为(0,0),圆的半径r=1,
故经过圆上一点M(1,0)的切线方程是x=1.
方法二 直接应用圆的切线方程的结论得,所求切线方程为1·x+0·y=12,即x=1.
5.(2020·临朐一中高一检测)若圆心坐标为(2,-1)的圆在直线x-y-1=0上截得的弦长为2,则这个圆的方程是( B )
A.(x-2)2+(y+1)2=2 B.(x-2)2+(y+1)2=4
C.(x-2)2+(y+1)2=8 D.(x-2)2+(y+1)2=16
[解析] 由题意得,设圆的方程为(x-2)2+(y+1)2=r2,圆心到直线x-y-1=0的距离为d==,再由圆的弦长公式,可得2=2?r2-d2=2,即r2=d2+2=4,所以这个圆的方程为(x-2)2+(y+1)2=4,故选B.
二、填空题
6.圆(x-3)2+(y-3)2=9上到直线3x+4y-11=0的距离等于1的点有__3__个.
[解析] 圆心(3,3)到直线3x+4y-11=0的距离,d==2,又r=3,
故有三个点到直线3x+4y-11=0的距离等于1.
7.(天津文)已知圆C的圆心在x轴的正半轴上,点M(0,)在圆C上,且圆心到直线2x-y=0的距离为,则圆C的方程为__(x-2)2+y2=9__.
[解析] 设圆心为(a,0)(a>0),则圆心到直线2x-y=0的距离d==,解得a=2,半径r==3,所以圆C的方程为(x-2)2+y2=9.
8.(2020·河北省石家庄市正定三中高二期中)已知圆C与直线x-6y-10=0相切于点(4,-1),且经过点(9,6),则圆C的方程为__(x-3)2+(y-5)2=37__.
[解析] 因为圆C与直线x-6y-10=0相切于点(4,-1),所以过点(4,-1)的直径所在直线的斜率为-=-6,该直线方程为y+1=-6(x-4),即6x+y-23=0.又圆心在以(4,-1),(9,6)两点为端点的线段的垂直平分线y-=-,即直线5x+7y-50=0上,由解得即圆心坐标为(3,5),所以半径为=,故所求圆的方程为(x-3)2+(y-5)2=37.
三、解答题
9.求满足下列条件的圆x2+y2=4的切线方程:
(1)经过点P(,1);
(2)斜率为-1;
(3)过点Q(3,0).
[解析] (1)∵点P(,1)在圆上.
∴所求切线方程为x+y-4=0.
(2)设圆的切线方程为y=-x+b,
代入圆的方程,整理得
2x2-2bx+b2-4=0,∵直线与圆相切,
∴Δ=(-2b)2-4×2(b2-4)=0.
解得b=±2.
∴所求切线方程为x+y±2=0.
也可用几何法d=r求解.
(3)解法一:∵32+02>4,∴点Q在圆外.
设切线方程为y=k(x-3),即kx-y-3k=0.
∵直线与圆相切,∴圆心到直线的距离等于半径,
∴=2,∴k=±,
∴所求切线方程为2x±y-6=0.
解法二:设切点为M(x0,y0),则过点M的切线方程为
x0x+y0y=4,∵点Q(3,0)在切线上,∴x0=①
又M(x0,y0)在圆x2+y2=4上,∴x+y=4②
由①②构成的方程组可解得
或
∴所求切线方程为
x+y=4或x-y=4,
即2x+y-6=0或2x-y-6=0.
10.(2020·本溪一中高一期中)已知点M(3,1),直线ax-y+4=0及圆(x-1)2+(y-2)2=4.
(1)求过点M的圆的切线方程;
(2)若直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2,求a的值.
[解析] (1)由题意知圆心的坐标为(1,2),半径r=2,
当过点M的直线的斜率不存在时,直线方程为x=3.
由圆心(1,2)到直线x=3的距离3-1=2=r知,此时,直线与圆相切.
当过点M的直线的斜率存在时,设直线为y-1=k(x-3),
即kx-y+1-3k=0.由题意知=2,
解得k=,
∴方程为3x-4y-5=0.
故过点M的圆的切线方程为x=3或3x-4y-5=0.
(2)∵圆心到直线ax-y+4=0的距离为=,
∴2+()2=4,
解得a=-.
B组·素养提升
一、选择题
1.(多选题)平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是( AB )
A.2x+y+5=0 B.2x+y-5=0
C.2x+y+=0 D.2x+y-=0
[解析] ∵所求直线与直线2x+y+1=0平行,∴设所求的直线方程为2x+y+m=0.
∵所求直线与圆x2+y2=5相切,
∴=,∴m=±5.
即所求的直线方程为2x+y+5=0或2x+y-5=0.
故选AB.
2.(多选题)在同一直角坐标系中,直线y=ax+a2与圆(x+a)2+y2=a2的位置不可能为( ABD )
[解析] 由题意,可得a2>0,直线y=ax+a2显然过点(0,a2),故ABD均不可能.
3.(2018·全国卷Ⅲ理,6)直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x-2)2+y2=2上,则△ABP面积的取值范围是( A )
A.[2,6] B.[4,8]
C.[,3] D.[2,3]
[解析] ∵直线x+y+2=0分别与x轴,y轴交于A,B两点,
∴A(-2,0),B(0,-2),则|AB|=2,
∵点P在圆(x-2)2+y2=2上,
∴圆心为(2,0),则圆心到直线距离d1==2,
故点P到直线x+y+2=0的距离d2的范围为[,3],
则S△ABP=|AB|d2=d2∈[2,6].
故答案选A.
4.设圆(x-3)2+(y+5)2=r2(r>0)上有且仅有两个点到直线4x-3y-2=0的距离等于1,则圆半径r的取值范围是( B )
A.3<r<5 B.4<r<6
C.r>4 D.r>5
[解析] 圆心C(3,-5),半径为r,圆心C到直线4x-3y-2=0的距离d==5,由于圆C上有且仅有两个点到直线4x-3y-2=0的距离等于1,则d-1<r<d+1,所以4<r<6.
二、填空题
5.如图所示,一座圆拱桥,当水面在某位置时,拱顶离水面2 m,水面宽12 m,当水面下降1 m后,水面宽为__2__m.
[解析] 以圆拱桥拱顶为坐标原点,以过拱顶的竖直直线
为y轴,建立直角坐标系,如图所示.
设圆心为C,水面所在弦的端点为A、B,
则由已知得A(6,-2).
设圆的半径为r,
则C(0,-r),即圆的方程为x2+(y+r)2=r2.①
将点A的坐标(6,-2)代入方程①,得
36+(r-2)2=r2,∴r=10.
∴圆的方程为x2+(y+10)2=100.②
当水面下降1 m后,可设点A′的坐标为(x0,-3)(x0>0),
将A′的坐标(x0,-3)代入方程②,得x0=.
∴水面下降1 m后,水面宽为2x0=2 m.
6.(2019·浙江卷,12)已知圆C的圆心坐标是(0,m),半径长是r.若直线2x-y+3=0与圆C相切于点A(-2,-1),则m=__-2__,r=____.
[解析] 根据题意画出图形,可知
A(-2,-1),C(0,m),B(0,3),
则AB==2,
AC==,
BC=|m-3|.
∵直线2x-y+3=0与圆C相切于点A,
∴∠BAC=90°,∴AB2+AC2=BC2.
即20+4+(m+1)2=(m-3)2,
解得m=-2.
因此r=AC==.
7.(2020·广东省汕头市高二期末)已知圆C的圆心与点(-2,1)关于直线y=x+1对称 ,直线3x+4y-11=0与圆C相交于A,B两点,且|AB|=6,则圆C的标准方程为__x2+(y+1)2=18__.
[解析] 设点(-2,1)关于直线y=x+1的对称点为C(x0,y0),则解得
即圆心C的坐标为(0,-1),
则圆心C到直线3x+4y-11=0的距离为
=3.
从而圆C的半径为=3,故圆C的方程为x2+(y+1)2=18.
三、解答题
8.(2020·邹城一中高一检测)已知方程x2+y2-2x-4y+m=0,m∈R.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且OM⊥ON(O为坐标原点),求m;
(3)在(2)的条件下,求以MN为直径的圆的方程.
[解析] (1)(x-1)2+(y-2)2=5-m,
∴方程表示圆时,m<5.
(2)设M(x1,y1),N(x2,y2),则x1=4-2y1,x2=4-2y2,
得x1x2=16-8(y1+y2)+4y1y2,
∵OM⊥ON,∴kOM·kON=·=-1,∴x1x2+y1y2=0,
∴16-8(y1+y2)+5y1y2=0①,
由,得5y2-16y+m+8=0,
∴y1+y2=,y1y2=.
代入①得m=.
(3)以MN为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0,
即x2+y2-(x1+x2)x-(y1+y2)y=0,
∴所求圆的方程为x2+y2-x-y=0.
9.已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.
(1)若m=4,求直线l被圆C所截得弦长的最大值;
(2)若直线l是圆心下方的切线,当a在(0,4]变化时,求m的取值范围.
[解析] (1)已知圆的标准方程是(x+a)2+(y-a)2=4a(0<a≤4),则圆心C的坐标是(-a,a),半径为2.
直线l的方程化为x-y+4=0,则圆心C到直线l的距离是=|2-a|.
设直线l被圆C所截得弦长为L,由弦长、圆心距和圆的半径之间的关系,得
L=2=2
=2.
∵0<a≤4,∴当a=3时,L的最大值为2.
(2)∵直线l与圆C相切,则有=2,
即|m-2a|=2.
∵点C在直线l的上方,∴a>-a+m,即2a>m,
∴2a-m=2,∴m=(-1)2-1.
∵0<a≤4,∴0<≤2,∴m∈[-1,8-4].
1.直线3x+4y-5=0与圆x2+y2=1的位置关系是( )
A.相交 B.相切
C.相离 D.无法判断
2.若直线l与圆C有公共点,则直线l与圆C的位置关系是( )
A.相交 B.相切
C.相离 D.相切或相交
3.直线x+2y-5+=0被圆x2+y2-2x-4y=0截得的弦长为( )
A.1 B.2
C.4 D.4
4.(全国卷Ⅰ,文)设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A、B两点,若|AB|=2,则圆C的面积为__ __.
5.已知圆C:x2+y2-4x+3=0,过原点的直线l与其交于不同的两点A、B.
(1)求直线l的斜率k的取值范围;
(2)求线段AB的中点P的轨迹方程.
A组·素养自测
一、选择题
1.(2021·北京市海淀区检测)直线3x+4y-13=0与圆(x-2)2+(y-3)2=1的位置关系是( )
A.相离 B.相交
C.相切 D.无法判定
2.已知直线ax+by+c=0(a、b、c都是正数)与圆x2+y2=1相切,则以a、b、c为三边长的三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不存在
3.(2020·九江一中高一期末)已知圆C:x2+y2=9,点P为直线x+2y-9=0上一动点,过点P向圆C引两条切线PA、PB,且A、B为切点,则直线AB经过定点( )
A.(4,8) B.(2,4)
C.(1,2) D.(9,0)
4.(2020·四川省南充市三模)已知圆的方程为x2+y2=1,则经过圆上一点M(1,0)的切线方程是( )
A.x=1 B.y=1
C.x+y=1 D.x-y=1
5.(2020·临朐一中高一检测)若圆心坐标为(2,-1)的圆在直线x-y-1=0上截得的弦长为2,则这个圆的方程是( )
A.(x-2)2+(y+1)2=2 B.(x-2)2+(y+1)2=4
C.(x-2)2+(y+1)2=8 D.(x-2)2+(y+1)2=16
二、填空题
6.圆(x-3)2+(y-3)2=9上到直线3x+4y-11=0的距离等于1的点有____个.
7.(天津文)已知圆C的圆心在x轴的正半轴上,点M(0,)在圆C上,且圆心到直线2x-y=0的距离为,则圆C的方程为____.
8.(2020·河北省石家庄市正定三中高二期中)已知圆C与直线x-6y-10=0相切于点(4,-1),且经过点(9,6),则圆C的方程为____.
三、解答题
9.求满足下列条件的圆x2+y2=4的切线方程:
(1)经过点P(,1);
(2)斜率为-1;
(3)过点Q(3,0).
10.(2020·本溪一中高一期中)已知点M(3,1),直线ax-y+4=0及圆(x-1)2+(y-2)2=4.
(1)求过点M的圆的切线方程;
(2)若直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2,求a的值.
B组·素养提升
一、选择题
1.(多选题)平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是( )
A.2x+y+5=0 B.2x+y-5=0
C.2x+y+=0 D.2x+y-=0
2.(多选题)在同一直角坐标系中,直线y=ax+a2与圆(x+a)2+y2=a2的位置不可能为( )
3.(2018·全国卷Ⅲ理,6)直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x-2)2+y2=2上,则△ABP面积的取值范围是( )
A.[2,6] B.[4,8]
C.[,3] D.[2,3]
4.设圆(x-3)2+(y+5)2=r2(r>0)上有且仅有两个点到直线4x-3y-2=0的距离等于1,则圆半径r的取值范围是( )
A.3<r<5 B.4<r<6
C.r>4 D.r>5
二、填空题
5.如图所示,一座圆拱桥,当水面在某位置时,拱顶离水面2 m,水面宽12 m,当水面下降1 m后,水面宽为____m.
6.(2019·浙江卷,12)已知圆C的圆心坐标是(0,m),半径长是r.若直线2x-y+3=0与圆C相切于点A(-2,-1),则m=____,r=____.
7.(2020·广东省汕头市高二期末)已知圆C的圆心与点(-2,1)关于直线y=x+1对称,直线3x+4y-11=0与圆C相交于A,B两点,且|AB|=6,则圆C的标准方程为____.
三、解答题
8.(2020·邹城一中高一检测)已知方程x2+y2-2x-4y+m=0,m∈R.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且OM⊥ON(O为坐标原点),求m;
(3)在(2)的条件下,求以MN为直径的圆的方程.
9.已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.
(1)若m=4,求直线l被圆C所截得弦长的最大值;
(2)若直线l是圆心下方的切线,当a在(0,4]变化时,求m的取值范围.
2.5.1直线与圆的位置关系
1.直线3x+4y-5=0与圆x2+y2=1的位置关系是( B )
A.相交 B.相切
C.相离 D.无法判断
[解析] d==1=r,∴选B.
2.若直线l与圆C有公共点,则直线l与圆C的位置关系是( D )
A.相交 B.相切
C.相离 D.相切或相交
[解析] 当只有一个公共点时,直线l与圆C相切;当有两个公共点时,直线l与圆C相交.
3.直线x+2y-5+=0被圆x2+y2-2x-4y=0截得的弦长为( C )
A.1 B.2
C.4 D.4
[解析] 依题意,圆的圆心为(1,2),半径r=,圆心到直线的距离d==1,所以结合图形可知弦长的一半为=2,故弦长为4.
4.(全国卷Ⅰ,文)设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A、B两点,若|AB|=2,则圆C的面积为__4π__.
[解析] 圆C的方程可化为x2+(y-a)2=a2+2,可得圆心的坐标为C(0,a),半径r=,所以圆心到直线x-y+2a=0的距离为=,所以()2+()2=()2,解得a2=2,所以圆C的半径为2,所以圆C的面积为4π.
5.已知圆C:x2+y2-4x+3=0,过原点的直线l与其交于不同的两点A、B.
(1)求直线l的斜率k的取值范围;
(2)求线段AB的中点P的轨迹方程.
[解析] (1)圆C的标准方程为(x-2)2+y2=1,
由题意可设直线l的方程为y=kx.
∵直线l与圆C有两个不同交点,
∴<1,
∴-<k<.
(2)设点P(x,y),∵点P为线段AB的中点,∴CP⊥OP.
∴kCP·kOP=-1,
即·=-1(x≠2且x≠0),
化简得x2+y2-2x=0.
由得
故点P的轨迹方程为x2+y2-2x=0(<x≤2).
A组·素养自测
一、选择题
1.(2021·北京市海淀区检测)直线3x+4y-13=0与圆(x-2)2+(y-3)2=1的位置关系是( C )
A.相离 B.相交
C.相切 D.无法判定
[解析] 由圆的方程可知,圆心坐标为(2,3),半径r=1,所以圆心到直线3x+4y-13=0的距离d==1=r,则直线与圆的位置关系为相切.
2.已知直线ax+by+c=0(a、b、c都是正数)与圆x2+y2=1相切,则以a、b、c为三边长的三角形是( B )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不存在
[解析] 由题意,得=1,
∴a2+b2=c2,故选B.
3.(2020·九江一中高一期末)已知圆C:x2+y2=9,点P为直线x+2y-9=0上一动点,过点P向圆C引两条切线PA、PB,且A、B为切点,则直线AB经过定点( C )
A.(4,8) B.(2,4)
C.(1,2) D.(9,0)
[解析] 设P(9-2b,b),由圆的切线公式,则直线lAB:(9-2b)x+by=9,即b(y-2x)+9x=9,
所以定点?.
4.(2020·四川省南充市三模)已知圆的方程为x2+y2=1,则经过圆上一点M(1,0)的切线方程是( A )
A.x=1 B.y=1
C.x+y=1 D.x-y=1
[解析] 方法一 由圆的方程为x2+y2=1,可知圆心的坐标为(0,0),圆的半径r=1,
故经过圆上一点M(1,0)的切线方程是x=1.
方法二 直接应用圆的切线方程的结论得,所求切线方程为1·x+0·y=12,即x=1.
5.(2020·临朐一中高一检测)若圆心坐标为(2,-1)的圆在直线x-y-1=0上截得的弦长为2,则这个圆的方程是( B )
A.(x-2)2+(y+1)2=2 B.(x-2)2+(y+1)2=4
C.(x-2)2+(y+1)2=8 D.(x-2)2+(y+1)2=16
[解析] 由题意得,设圆的方程为(x-2)2+(y+1)2=r2,圆心到直线x-y-1=0的距离为d==,再由圆的弦长公式,可得2=2?r2-d2=2,即r2=d2+2=4,所以这个圆的方程为(x-2)2+(y+1)2=4,故选B.
二、填空题
6.圆(x-3)2+(y-3)2=9上到直线3x+4y-11=0的距离等于1的点有__3__个.
[解析] 圆心(3,3)到直线3x+4y-11=0的距离,d==2,又r=3,
故有三个点到直线3x+4y-11=0的距离等于1.
7.(天津文)已知圆C的圆心在x轴的正半轴上,点M(0,)在圆C上,且圆心到直线2x-y=0的距离为,则圆C的方程为__(x-2)2+y2=9__.
[解析] 设圆心为(a,0)(a>0),则圆心到直线2x-y=0的距离d==,解得a=2,半径r==3,所以圆C的方程为(x-2)2+y2=9.
8.(2020·河北省石家庄市正定三中高二期中)已知圆C与直线x-6y-10=0相切于点(4,-1),且经过点(9,6),则圆C的方程为__(x-3)2+(y-5)2=37__.
[解析] 因为圆C与直线x-6y-10=0相切于点(4,-1),所以过点(4,-1)的直径所在直线的斜率为-=-6,该直线方程为y+1=-6(x-4),即6x+y-23=0.又圆心在以(4,-1),(9,6)两点为端点的线段的垂直平分线y-=-,即直线5x+7y-50=0上,由解得即圆心坐标为(3,5),所以半径为=,故所求圆的方程为(x-3)2+(y-5)2=37.
三、解答题
9.求满足下列条件的圆x2+y2=4的切线方程:
(1)经过点P(,1);
(2)斜率为-1;
(3)过点Q(3,0).
[解析] (1)∵点P(,1)在圆上.
∴所求切线方程为x+y-4=0.
(2)设圆的切线方程为y=-x+b,
代入圆的方程,整理得
2x2-2bx+b2-4=0,∵直线与圆相切,
∴Δ=(-2b)2-4×2(b2-4)=0.
解得b=±2.
∴所求切线方程为x+y±2=0.
也可用几何法d=r求解.
(3)解法一:∵32+02>4,∴点Q在圆外.
设切线方程为y=k(x-3),即kx-y-3k=0.
∵直线与圆相切,∴圆心到直线的距离等于半径,
∴=2,∴k=±,
∴所求切线方程为2x±y-6=0.
解法二:设切点为M(x0,y0),则过点M的切线方程为
x0x+y0y=4,∵点Q(3,0)在切线上,∴x0=①
又M(x0,y0)在圆x2+y2=4上,∴x+y=4②
由①②构成的方程组可解得
或
∴所求切线方程为
x+y=4或x-y=4,
即2x+y-6=0或2x-y-6=0.
10.(2020·本溪一中高一期中)已知点M(3,1),直线ax-y+4=0及圆(x-1)2+(y-2)2=4.
(1)求过点M的圆的切线方程;
(2)若直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2,求a的值.
[解析] (1)由题意知圆心的坐标为(1,2),半径r=2,
当过点M的直线的斜率不存在时,直线方程为x=3.
由圆心(1,2)到直线x=3的距离3-1=2=r知,此时,直线与圆相切.
当过点M的直线的斜率存在时,设直线为y-1=k(x-3),
即kx-y+1-3k=0.由题意知=2,
解得k=,
∴方程为3x-4y-5=0.
故过点M的圆的切线方程为x=3或3x-4y-5=0.
(2)∵圆心到直线ax-y+4=0的距离为=,
∴2+()2=4,
解得a=-.
B组·素养提升
一、选择题
1.(多选题)平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是( AB )
A.2x+y+5=0 B.2x+y-5=0
C.2x+y+=0 D.2x+y-=0
[解析] ∵所求直线与直线2x+y+1=0平行,∴设所求的直线方程为2x+y+m=0.
∵所求直线与圆x2+y2=5相切,
∴=,∴m=±5.
即所求的直线方程为2x+y+5=0或2x+y-5=0.
故选AB.
2.(多选题)在同一直角坐标系中,直线y=ax+a2与圆(x+a)2+y2=a2的位置不可能为( ABD )
[解析] 由题意,可得a2>0,直线y=ax+a2显然过点(0,a2),故ABD均不可能.
3.(2018·全国卷Ⅲ理,6)直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x-2)2+y2=2上,则△ABP面积的取值范围是( A )
A.[2,6] B.[4,8]
C.[,3] D.[2,3]
[解析] ∵直线x+y+2=0分别与x轴,y轴交于A,B两点,
∴A(-2,0),B(0,-2),则|AB|=2,
∵点P在圆(x-2)2+y2=2上,
∴圆心为(2,0),则圆心到直线距离d1==2,
故点P到直线x+y+2=0的距离d2的范围为[,3],
则S△ABP=|AB|d2=d2∈[2,6].
故答案选A.
4.设圆(x-3)2+(y+5)2=r2(r>0)上有且仅有两个点到直线4x-3y-2=0的距离等于1,则圆半径r的取值范围是( B )
A.3<r<5 B.4<r<6
C.r>4 D.r>5
[解析] 圆心C(3,-5),半径为r,圆心C到直线4x-3y-2=0的距离d==5,由于圆C上有且仅有两个点到直线4x-3y-2=0的距离等于1,则d-1<r<d+1,所以4<r<6.
二、填空题
5.如图所示,一座圆拱桥,当水面在某位置时,拱顶离水面2 m,水面宽12 m,当水面下降1 m后,水面宽为__2__m.
[解析] 以圆拱桥拱顶为坐标原点,以过拱顶的竖直直线
为y轴,建立直角坐标系,如图所示.
设圆心为C,水面所在弦的端点为A、B,
则由已知得A(6,-2).
设圆的半径为r,
则C(0,-r),即圆的方程为x2+(y+r)2=r2.①
将点A的坐标(6,-2)代入方程①,得
36+(r-2)2=r2,∴r=10.
∴圆的方程为x2+(y+10)2=100.②
当水面下降1 m后,可设点A′的坐标为(x0,-3)(x0>0),
将A′的坐标(x0,-3)代入方程②,得x0=.
∴水面下降1 m后,水面宽为2x0=2 m.
6.(2019·浙江卷,12)已知圆C的圆心坐标是(0,m),半径长是r.若直线2x-y+3=0与圆C相切于点A(-2,-1),则m=__-2__,r=____.
[解析] 根据题意画出图形,可知
A(-2,-1),C(0,m),B(0,3),
则AB==2,
AC==,
BC=|m-3|.
∵直线2x-y+3=0与圆C相切于点A,
∴∠BAC=90°,∴AB2+AC2=BC2.
即20+4+(m+1)2=(m-3)2,
解得m=-2.
因此r=AC==.
7.(2020·广东省汕头市高二期末)已知圆C的圆心与点(-2,1)关于直线y=x+1对称 ,直线3x+4y-11=0与圆C相交于A,B两点,且|AB|=6,则圆C的标准方程为__x2+(y+1)2=18__.
[解析] 设点(-2,1)关于直线y=x+1的对称点为C(x0,y0),则解得
即圆心C的坐标为(0,-1),
则圆心C到直线3x+4y-11=0的距离为
=3.
从而圆C的半径为=3,故圆C的方程为x2+(y+1)2=18.
三、解答题
8.(2020·邹城一中高一检测)已知方程x2+y2-2x-4y+m=0,m∈R.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且OM⊥ON(O为坐标原点),求m;
(3)在(2)的条件下,求以MN为直径的圆的方程.
[解析] (1)(x-1)2+(y-2)2=5-m,
∴方程表示圆时,m<5.
(2)设M(x1,y1),N(x2,y2),则x1=4-2y1,x2=4-2y2,
得x1x2=16-8(y1+y2)+4y1y2,
∵OM⊥ON,∴kOM·kON=·=-1,∴x1x2+y1y2=0,
∴16-8(y1+y2)+5y1y2=0①,
由,得5y2-16y+m+8=0,
∴y1+y2=,y1y2=.
代入①得m=.
(3)以MN为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0,
即x2+y2-(x1+x2)x-(y1+y2)y=0,
∴所求圆的方程为x2+y2-x-y=0.
9.已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.
(1)若m=4,求直线l被圆C所截得弦长的最大值;
(2)若直线l是圆心下方的切线,当a在(0,4]变化时,求m的取值范围.
[解析] (1)已知圆的标准方程是(x+a)2+(y-a)2=4a(0<a≤4),则圆心C的坐标是(-a,a),半径为2.
直线l的方程化为x-y+4=0,则圆心C到直线l的距离是=|2-a|.
设直线l被圆C所截得弦长为L,由弦长、圆心距和圆的半径之间的关系,得
L=2=2
=2.
∵0<a≤4,∴当a=3时,L的最大值为2.
(2)∵直线l与圆C相切,则有=2,
即|m-2a|=2.
∵点C在直线l的上方,∴a>-a+m,即2a>m,
∴2a-m=2,∴m=(-1)2-1.
∵0<a≤4,∴0<≤2,∴m∈[-1,8-4].
