七年级数学下册试题 一课一练《相交线与平行线》习题1-北师大版(word版含答案)
文档属性
| 名称 | 七年级数学下册试题 一课一练《相交线与平行线》习题1-北师大版(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 96.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 00:00:00 | ||
图片预览




文档简介
《相交线与平行线》习题1
一、选择题
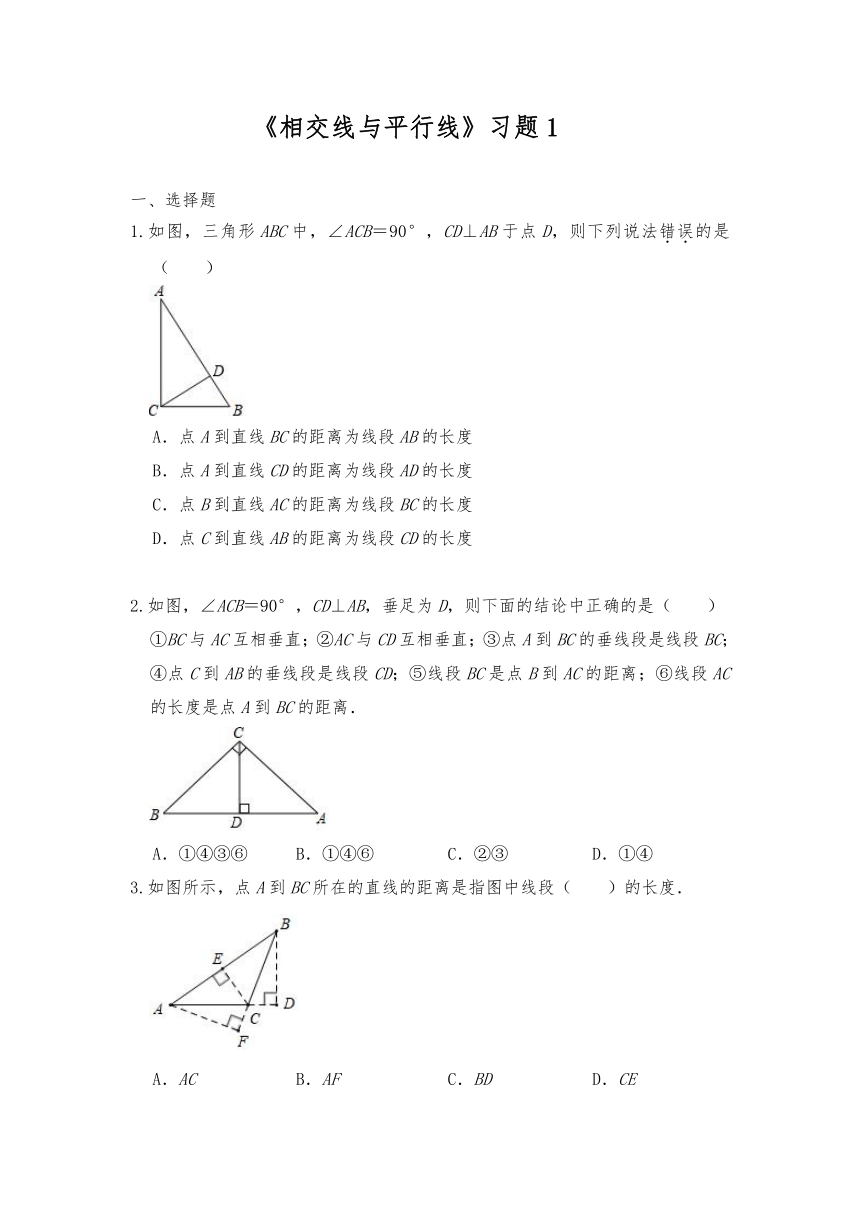
1.如图,三角形ABC中,∠ACB=90°,CD⊥AB于点D,则下列说法错误的是( )
A.点A到直线BC的距离为线段AB的长度
B.点A到直线CD的距离为线段AD的长度
C.点B到直线AC的距离为线段BC的长度
D.点C到直线AB的距离为线段CD的长度
2.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是( )
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;④点C到AB的垂线段是线段CD;⑤线段BC是点B到AC的距离;⑥线段AC的长度是点A到BC的距离.
A.①④③⑥
B.①④⑥
C.②③
D.①④
3.如图所示,点A到BC所在的直线的距离是指图中线段( )的长度.
A.AC
B.AF
C.BD
D.CE
4.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段CD的长度是C点到AB的距离;②线段AC是A点到BC的距离;
③AB>AC>CD;④线段BC是B到AC的距离;⑤CD<BC<AB.
A.2个
B.3个
C.4个
D.5个
5.在同一平面内的n条直线两两相交,最多共有36个交点,则n=( )
A.7
B.8
C.9
D.10
6.两条直线最多有一个交点,三条直线最多有三个交点,四条直线最多有6个交点,……,那么7条直线最多( )
A.28个交点
B.24个交点
C.21个交点
D.15个交点
7.同一平面内两两相交的四条直线,最多有m个交点,最少有n个交点,那么mn是( )
A.1
B.6
C.8
D.4
8.观察下列图形,并阅读图形下面的相关文字,如图所示:两条直线相交,最多有一个交点;三条直线相交,最多有三个交点;四条直线相交,最多有6个交点,像这样,11条直线相交,最多交点的个数是( )
A.40个
B.50个
C.55个
D.66个
9.如图,下列说法中错误的是( )
A.∠3和∠5是同位角
B.∠4和∠5是同旁内角
C.∠2和∠4是对顶角
D.∠2和∠5是内错角
10.同学们可仿照图用双手表示“三线八角”图形(两大拇指代表被截直线,食指代表截线).下面三幅图依次表示( )
A.同位角、同旁内角、内错角
B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角
D.同位角、内错角、对顶角
11.如图,同位角共有( )对.
A.6
B.5
C.8
D.7
12.如图,下列结论正确的是( )
A.∠4和∠5是同旁内角
B.∠3和∠2是对顶角
C.∠3和∠5是内错角
D.∠1和∠5是同位角
13.下列说法中,正确的是( )
A.两条不相交的直线叫平行线
B.一条直线的平行线有且只有一条
C.若直线a∥b,a∥c,则b∥c
D.两条直线不相交就平行
二、解答题
1.如图,在直线MN的异侧有A、B两点,按要求画图取点,并注明画图取点的依据.
(1)在直线MN上取一点C,使线段AC最短.依据是
.
(2)在直线MN上取一点D,使线段AD+BD最短.依据是
.
2.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短并说明根据.
3.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
4.如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l上画出车站的位置(用点M表示),依据是
;
(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是
.
5.已知:如图,∠1+∠2=180°,∠A=∠D.求证:AB∥CD.(在每步证明过程后面注明理由)
6.如图,AD⊥BC于D,EF⊥BC于F,∠1=∠2,AB与DG平行吗?为什么?
7.如图,已知点A.D,B在同一直线上,∠1=∠2,∠3=∠E,试判断DE、BC有怎样的位置关系,并说明理由.
8.如图:已知∠1+∠2=180°,∠3=∠B,请问AB与DE是否平行,并说明理由.
答案
一、选择题
1.A.2.B.3.B.4.B.5.C.6.C.7.B.8.C.9.D.10.B.11.A.12.C.13.C.
二、解答题
1.解:(1)过A作AC⊥MN,根据:垂线段最短.
(2)连接AB交MN于D,根据是:两点之间线段最短.
2.解:(1)∵两点之间线段最短,
∴连接AD,BC交于H,则H为蓄水池位置,它到四个村庄距离之和最小.
(2)过H作HG⊥EF,垂足为G.
“过直线外一点与直线上各点的连线中,垂线段最短”是把河水引入蓄水池H中开渠最短的根据.
3.解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
4.解:(1)如图,点M即为所示.依据是直线外一点与直线上各点连接的所有线段中垂线段最短
(2)如图,点N即为所示.依据是两点之间线段最短;
故答案为:直线外一点与直线上各点连接的所有线段中垂线段最短;两点之间线段最短.
5.证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(对顶角相等),
∵∠1+∠2=180°(已知),
∴∠CGD+∠2=180°(等量代换),
∴AE∥FD(同旁内角互补,两直线平行),
∴∠A=∠BFD(两直线平行,同位角相等),
又∵∠A=∠D(已知),
∴∠BFD=∠D(等量代换),
∴AB∥CD(内错角相等,两直线平行).
6.解:结论:AB∥DG.
理由:∵AD⊥BC于D,EF⊥BC于F,
∴AD∥EF,
∴∠1=∠BAD,
∵∠1=∠2,
∴∠BAD=∠2,
∴AB∥DG.
7.解:DE∥BC.
证明:∵∠1=∠2,∠AOE=∠COD(对顶角相等),
∴在△AOE和△COD中,∠CDO=∠E(三角形内角和定理);
∵∠3=∠E,
∴∠CDO=∠3,
∴DE∥BC(内错角相等,两直线平行).
8.解:结论:AB∥DE.
理由:∵∠1+∠ADC=180°(平角的定义),
又∵∠1+∠2=180°(已知),
∴∠ADC=∠2(等量代换),
∴EF∥DC(同位角相等两直线平行),
∴∠3=∠EDC(两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴∠EDC=∠B(等量代换),
∴AB∥DE(同位角相等两直线平行).
一、选择题
1.如图,三角形ABC中,∠ACB=90°,CD⊥AB于点D,则下列说法错误的是( )
A.点A到直线BC的距离为线段AB的长度
B.点A到直线CD的距离为线段AD的长度
C.点B到直线AC的距离为线段BC的长度
D.点C到直线AB的距离为线段CD的长度
2.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是( )
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;④点C到AB的垂线段是线段CD;⑤线段BC是点B到AC的距离;⑥线段AC的长度是点A到BC的距离.
A.①④③⑥
B.①④⑥
C.②③
D.①④
3.如图所示,点A到BC所在的直线的距离是指图中线段( )的长度.
A.AC
B.AF
C.BD
D.CE
4.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段CD的长度是C点到AB的距离;②线段AC是A点到BC的距离;
③AB>AC>CD;④线段BC是B到AC的距离;⑤CD<BC<AB.
A.2个
B.3个
C.4个
D.5个
5.在同一平面内的n条直线两两相交,最多共有36个交点,则n=( )
A.7
B.8
C.9
D.10
6.两条直线最多有一个交点,三条直线最多有三个交点,四条直线最多有6个交点,……,那么7条直线最多( )
A.28个交点
B.24个交点
C.21个交点
D.15个交点
7.同一平面内两两相交的四条直线,最多有m个交点,最少有n个交点,那么mn是( )
A.1
B.6
C.8
D.4
8.观察下列图形,并阅读图形下面的相关文字,如图所示:两条直线相交,最多有一个交点;三条直线相交,最多有三个交点;四条直线相交,最多有6个交点,像这样,11条直线相交,最多交点的个数是( )
A.40个
B.50个
C.55个
D.66个
9.如图,下列说法中错误的是( )
A.∠3和∠5是同位角
B.∠4和∠5是同旁内角
C.∠2和∠4是对顶角
D.∠2和∠5是内错角
10.同学们可仿照图用双手表示“三线八角”图形(两大拇指代表被截直线,食指代表截线).下面三幅图依次表示( )
A.同位角、同旁内角、内错角
B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角
D.同位角、内错角、对顶角
11.如图,同位角共有( )对.
A.6
B.5
C.8
D.7
12.如图,下列结论正确的是( )
A.∠4和∠5是同旁内角
B.∠3和∠2是对顶角
C.∠3和∠5是内错角
D.∠1和∠5是同位角
13.下列说法中,正确的是( )
A.两条不相交的直线叫平行线
B.一条直线的平行线有且只有一条
C.若直线a∥b,a∥c,则b∥c
D.两条直线不相交就平行
二、解答题
1.如图,在直线MN的异侧有A、B两点,按要求画图取点,并注明画图取点的依据.
(1)在直线MN上取一点C,使线段AC最短.依据是
.
(2)在直线MN上取一点D,使线段AD+BD最短.依据是
.
2.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短并说明根据.
3.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
4.如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l上画出车站的位置(用点M表示),依据是
;
(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是
.
5.已知:如图,∠1+∠2=180°,∠A=∠D.求证:AB∥CD.(在每步证明过程后面注明理由)
6.如图,AD⊥BC于D,EF⊥BC于F,∠1=∠2,AB与DG平行吗?为什么?
7.如图,已知点A.D,B在同一直线上,∠1=∠2,∠3=∠E,试判断DE、BC有怎样的位置关系,并说明理由.
8.如图:已知∠1+∠2=180°,∠3=∠B,请问AB与DE是否平行,并说明理由.
答案
一、选择题
1.A.2.B.3.B.4.B.5.C.6.C.7.B.8.C.9.D.10.B.11.A.12.C.13.C.
二、解答题
1.解:(1)过A作AC⊥MN,根据:垂线段最短.
(2)连接AB交MN于D,根据是:两点之间线段最短.
2.解:(1)∵两点之间线段最短,
∴连接AD,BC交于H,则H为蓄水池位置,它到四个村庄距离之和最小.
(2)过H作HG⊥EF,垂足为G.
“过直线外一点与直线上各点的连线中,垂线段最短”是把河水引入蓄水池H中开渠最短的根据.
3.解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
4.解:(1)如图,点M即为所示.依据是直线外一点与直线上各点连接的所有线段中垂线段最短
(2)如图,点N即为所示.依据是两点之间线段最短;
故答案为:直线外一点与直线上各点连接的所有线段中垂线段最短;两点之间线段最短.
5.证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(对顶角相等),
∵∠1+∠2=180°(已知),
∴∠CGD+∠2=180°(等量代换),
∴AE∥FD(同旁内角互补,两直线平行),
∴∠A=∠BFD(两直线平行,同位角相等),
又∵∠A=∠D(已知),
∴∠BFD=∠D(等量代换),
∴AB∥CD(内错角相等,两直线平行).
6.解:结论:AB∥DG.
理由:∵AD⊥BC于D,EF⊥BC于F,
∴AD∥EF,
∴∠1=∠BAD,
∵∠1=∠2,
∴∠BAD=∠2,
∴AB∥DG.
7.解:DE∥BC.
证明:∵∠1=∠2,∠AOE=∠COD(对顶角相等),
∴在△AOE和△COD中,∠CDO=∠E(三角形内角和定理);
∵∠3=∠E,
∴∠CDO=∠3,
∴DE∥BC(内错角相等,两直线平行).
8.解:结论:AB∥DE.
理由:∵∠1+∠ADC=180°(平角的定义),
又∵∠1+∠2=180°(已知),
∴∠ADC=∠2(等量代换),
∴EF∥DC(同位角相等两直线平行),
∴∠3=∠EDC(两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴∠EDC=∠B(等量代换),
∴AB∥DE(同位角相等两直线平行).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
