8.3动能和动能定理 学案
文档属性
| 名称 | 8.3动能和动能定理 学案 |  | |
| 格式 | docx | ||
| 文件大小 | 216.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-31 08:44:48 | ||
图片预览

文档简介
学习内容:《
8.3动能和动能定理2》
总第_____课时
课标核心素养要求
进一步理解动能定理,领会应用动能定理解题的优越性
学习目标
会利用动能定理分析变力做功、曲线运动以及多过程问题.
学习重点
利用动能定理分析变力做功、曲线运动以及多过程问题
学习过程
教学笔记
【自主学习】
回顾:功的计算式、动能定理表达式
【合作学习·难点探究】
任务一、能利用动能定理求变力做功
指导:
1.动能定理不仅适用于求恒力做的功,也适用于求变力做的功,同时因为不涉及变力作用的过程分析,应用非常方便.
2.当物体受到一个变力和几个恒力作用时,可以用动能定理间接求变力做的功,即W变+W其他=ΔEk.
【例1】一个质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平拉力F作用下,从平衡位置P点缓慢地移动到Q点,OQ与OP的夹角为θ,如图所示,重力加速度为g,则拉力F所做的功为( )
mglcos
θ
B.mgl(1-cos
θ)
C.Flcos
θ
D.Flsin
θ
【针对训练1】 如图所示为一水平的转台,半径为R,一质量为m的滑块放在转台的边缘,已知滑块与转台间的动摩擦因数为μ,且最大静摩擦力等于滑动摩擦力,重力加速度为g.若转台的转速由零逐渐增大,当滑块在转台上刚好发生相对滑动时,转台对滑块所做的功为( )
A.μmgR
B.2πmgR
C.2μmgR
D.0
任务二、利用动能定理分析多过程问题
指导:
1.对于多个物理过程要仔细分析,将复杂的过程分割成一个一个子过程,分别对每个过程分析,得出每个过程遵循的规律,当每个过程都可以应用动能定理时,可以选择分段或全程应用动能定理.当题目不涉及中间量时,选择全程应用动能定理更简单、方便.
2.选择全程应用动能定理时,要注意有些力不是全过程都作用的,必须根据不同的情况区别对待,弄清楚物体所受的力在哪段位移上做功、做正功还是负功,正确写出总功.
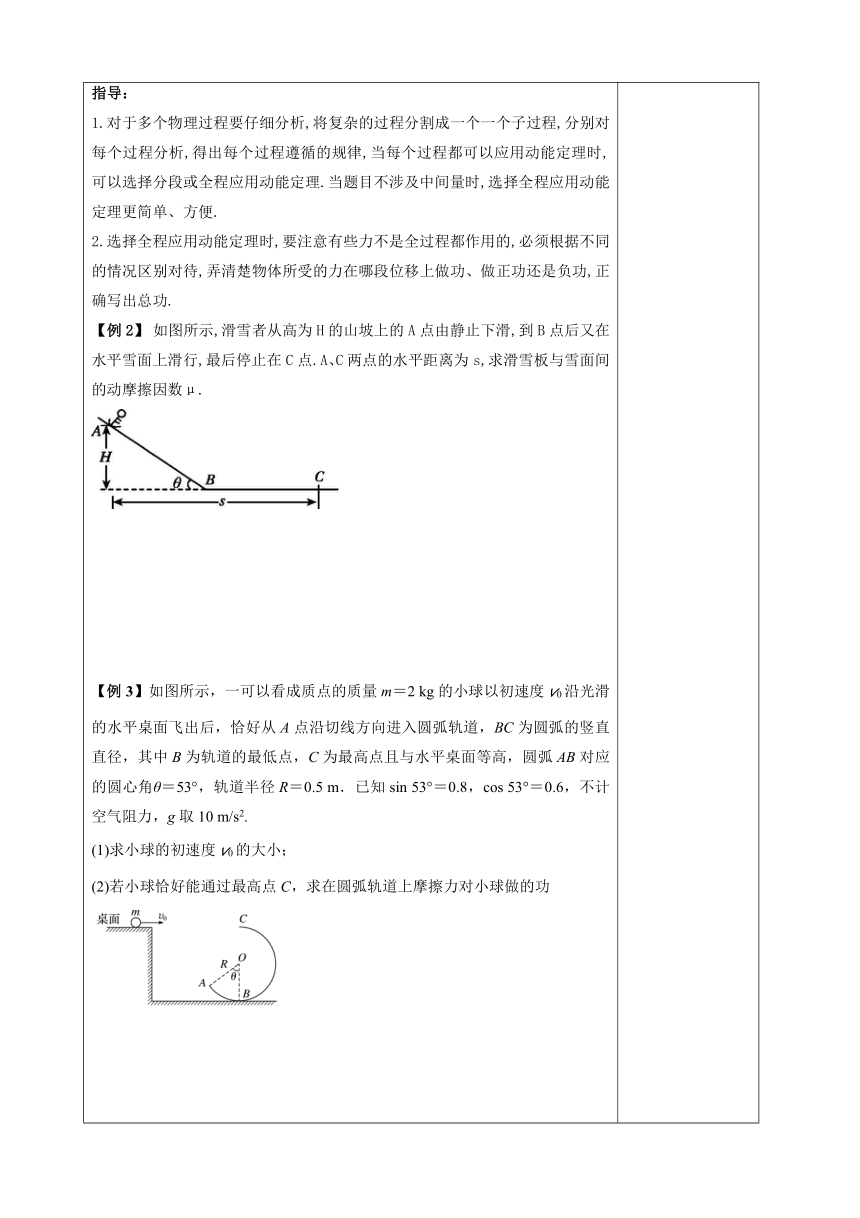
【例2】
如图所示,滑雪者从高为H的山坡上的A点由静止下滑,到B点后又在水平雪面上滑行,最后停止在C点.A、C两点的水平距离为s,求滑雪板与雪面间的动摩擦因数μ.
【例3】如图所示,一可以看成质点的质量m=2
kg的小球以初速度v0沿光滑的水平桌面飞出后,恰好从A点沿切线方向进入圆弧轨道,BC为圆弧的竖直直径,其中B为轨道的最低点,C为最高点且与水平桌面等高,圆弧AB对应的圆心角θ=53°,轨道半径R=0.5
m.已知sin
53°=0.8,cos
53°=0.6,不计空气阻力,g取10
m/s2.
(1)求小球的初速度v0的大小;
(2)若小球恰好能通过最高点C,求在圆弧轨道上摩擦力对小球做的功
【例4】如图所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,BC是水平的,长度d=0.5
m,盆边缘距地面的高度为h=0.3
m.在A处放一个质量为m的小物块并让其从静止开始下滑(图中小物块未画出).已知盆内侧壁是光滑的,而盆底BC与小物块间的动摩擦因数μ=0.1.小物块在盆内来回滑动直至最后静止,则小物块最终停下的位置到B点的距离为( )
A.0.5
m
B.0.25
m
C.0.1
m
D.0
任务三、能处理动能定理和图像结合问题
指导:
1.观察给出的图像,弄清横、纵坐标所对应的物理量及图线所表示的物理意义.
2.根据物理规律推导横、纵坐标所对应的物理量间的函数关系式,结合图像找出图线的斜率、截距、交点、图线与横坐标轴所包围的面积的物理意义.
【例5】质量为1
kg的物体在粗糙的水平地面上受到一个水平外力F的作用而运动,如图4甲所示,外力F和物体克服摩擦力Ff做的功W与物体位移x的关系如图乙所示,重力加速度g取10
m/s2.下列说法错误的是( )
A.物体与地面间的动摩擦因数为0.2
B.物体的最大位移为13
m
C.前3
m运动过程中,物体的加速度大小为3
m/s2
D.x=9
m时,物体的速度大小为3
m/s
【针对训练2】在某一粗糙的水平面上,一质量为2
kg的物体在水平恒定拉力的作用下做匀速直线运动,当运动一段时间后,拉力逐渐减小,且当拉力减小到零时,物体刚好停止运动,图中给出了拉力随位移变化的关系图像.已知重力加速度g取10
m/s2.根据以上信息能精确得出或估算得出的物理量有(
)
A.物体与水平面间的动摩擦因数
B.合外力对物体所做的功
C.物体做匀速运动时的速度
D.物体运动的时间
【达标训练·限时检测】
质量为m的物体以初速度v0沿水平面向左开始运动,起始点A与一水平轻弹簧O端相距s,如图所示.已知物体与水平面间的动摩擦因数为μ,物体与弹簧接触后,弹簧的最大压缩量为x,重力加速度为g,则从开始接触到弹簧被压缩至最短(弹簧始终在弹性限度内),物体克服弹簧弹力所做的功为( )
A.mv02-μmg(s+x)
B.mv02-μmgx
C.μmgs
D.μmg(s+x)
2、如图所示,在水平地面上虚线位置处有一个质量m=1
kg的小滑块P,P与水平地面间的动摩擦因数为μ=0.5.给P一个水平向右的初速度v0=6
m/s,P开始运动,已知P在虚线右侧总会受到大小为10
N且与水平方向成θ=37°角的斜向左上的恒定作用力F,g取10
m/s2,sin
37°=0.6,cos
37°=0.8.求:
(1)P向右运动的最大距离;
(2)P最终所在位置到虚线的距离.
3、如图所示,一长L=0.45
m、不可伸长的轻绳上端悬挂于M点,下端系一质量m=1.0
kg的小球,CDE是一竖直固定的圆弧形轨道,半径R=0.50
m,OC与竖直方向的夹角θ=60°,现将小球拉到A点(保持绳绷直且水平)由静止释放,当它经过B点时绳恰好被拉断,小球平抛后,从圆弧轨道的C点沿切线方向进入轨道,刚好能到达圆弧形轨道的最高点E,重力加速度g取10
m/s2,不计空气阻力,求:
(1)小球到B点时的速度大小;
(2)轻绳所受的最大拉力大小;
(3)小球在圆弧形轨道上运动时克服阻力做的功.
【反思总结】
答案
【例1】B
【针对训练1】A
【例2】μ=H/s
【例3】(1)3
m/s (2)-4
J
【例4】D
【例5】 ACD
【针对训练2】ABC
【达标训练·限时检测】
A
2、(1)
1.8
(2)
2.16
3、(1)3
m/s (2)30
N (3)8
J
8.3动能和动能定理2》
总第_____课时
课标核心素养要求
进一步理解动能定理,领会应用动能定理解题的优越性
学习目标
会利用动能定理分析变力做功、曲线运动以及多过程问题.
学习重点
利用动能定理分析变力做功、曲线运动以及多过程问题
学习过程
教学笔记
【自主学习】
回顾:功的计算式、动能定理表达式
【合作学习·难点探究】
任务一、能利用动能定理求变力做功
指导:
1.动能定理不仅适用于求恒力做的功,也适用于求变力做的功,同时因为不涉及变力作用的过程分析,应用非常方便.
2.当物体受到一个变力和几个恒力作用时,可以用动能定理间接求变力做的功,即W变+W其他=ΔEk.
【例1】一个质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平拉力F作用下,从平衡位置P点缓慢地移动到Q点,OQ与OP的夹角为θ,如图所示,重力加速度为g,则拉力F所做的功为( )
mglcos
θ
B.mgl(1-cos
θ)
C.Flcos
θ
D.Flsin
θ
【针对训练1】 如图所示为一水平的转台,半径为R,一质量为m的滑块放在转台的边缘,已知滑块与转台间的动摩擦因数为μ,且最大静摩擦力等于滑动摩擦力,重力加速度为g.若转台的转速由零逐渐增大,当滑块在转台上刚好发生相对滑动时,转台对滑块所做的功为( )
A.μmgR
B.2πmgR
C.2μmgR
D.0
任务二、利用动能定理分析多过程问题
指导:
1.对于多个物理过程要仔细分析,将复杂的过程分割成一个一个子过程,分别对每个过程分析,得出每个过程遵循的规律,当每个过程都可以应用动能定理时,可以选择分段或全程应用动能定理.当题目不涉及中间量时,选择全程应用动能定理更简单、方便.
2.选择全程应用动能定理时,要注意有些力不是全过程都作用的,必须根据不同的情况区别对待,弄清楚物体所受的力在哪段位移上做功、做正功还是负功,正确写出总功.
【例2】
如图所示,滑雪者从高为H的山坡上的A点由静止下滑,到B点后又在水平雪面上滑行,最后停止在C点.A、C两点的水平距离为s,求滑雪板与雪面间的动摩擦因数μ.
【例3】如图所示,一可以看成质点的质量m=2
kg的小球以初速度v0沿光滑的水平桌面飞出后,恰好从A点沿切线方向进入圆弧轨道,BC为圆弧的竖直直径,其中B为轨道的最低点,C为最高点且与水平桌面等高,圆弧AB对应的圆心角θ=53°,轨道半径R=0.5
m.已知sin
53°=0.8,cos
53°=0.6,不计空气阻力,g取10
m/s2.
(1)求小球的初速度v0的大小;
(2)若小球恰好能通过最高点C,求在圆弧轨道上摩擦力对小球做的功
【例4】如图所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,BC是水平的,长度d=0.5
m,盆边缘距地面的高度为h=0.3
m.在A处放一个质量为m的小物块并让其从静止开始下滑(图中小物块未画出).已知盆内侧壁是光滑的,而盆底BC与小物块间的动摩擦因数μ=0.1.小物块在盆内来回滑动直至最后静止,则小物块最终停下的位置到B点的距离为( )
A.0.5
m
B.0.25
m
C.0.1
m
D.0
任务三、能处理动能定理和图像结合问题
指导:
1.观察给出的图像,弄清横、纵坐标所对应的物理量及图线所表示的物理意义.
2.根据物理规律推导横、纵坐标所对应的物理量间的函数关系式,结合图像找出图线的斜率、截距、交点、图线与横坐标轴所包围的面积的物理意义.
【例5】质量为1
kg的物体在粗糙的水平地面上受到一个水平外力F的作用而运动,如图4甲所示,外力F和物体克服摩擦力Ff做的功W与物体位移x的关系如图乙所示,重力加速度g取10
m/s2.下列说法错误的是( )
A.物体与地面间的动摩擦因数为0.2
B.物体的最大位移为13
m
C.前3
m运动过程中,物体的加速度大小为3
m/s2
D.x=9
m时,物体的速度大小为3
m/s
【针对训练2】在某一粗糙的水平面上,一质量为2
kg的物体在水平恒定拉力的作用下做匀速直线运动,当运动一段时间后,拉力逐渐减小,且当拉力减小到零时,物体刚好停止运动,图中给出了拉力随位移变化的关系图像.已知重力加速度g取10
m/s2.根据以上信息能精确得出或估算得出的物理量有(
)
A.物体与水平面间的动摩擦因数
B.合外力对物体所做的功
C.物体做匀速运动时的速度
D.物体运动的时间
【达标训练·限时检测】
质量为m的物体以初速度v0沿水平面向左开始运动,起始点A与一水平轻弹簧O端相距s,如图所示.已知物体与水平面间的动摩擦因数为μ,物体与弹簧接触后,弹簧的最大压缩量为x,重力加速度为g,则从开始接触到弹簧被压缩至最短(弹簧始终在弹性限度内),物体克服弹簧弹力所做的功为( )
A.mv02-μmg(s+x)
B.mv02-μmgx
C.μmgs
D.μmg(s+x)
2、如图所示,在水平地面上虚线位置处有一个质量m=1
kg的小滑块P,P与水平地面间的动摩擦因数为μ=0.5.给P一个水平向右的初速度v0=6
m/s,P开始运动,已知P在虚线右侧总会受到大小为10
N且与水平方向成θ=37°角的斜向左上的恒定作用力F,g取10
m/s2,sin
37°=0.6,cos
37°=0.8.求:
(1)P向右运动的最大距离;
(2)P最终所在位置到虚线的距离.
3、如图所示,一长L=0.45
m、不可伸长的轻绳上端悬挂于M点,下端系一质量m=1.0
kg的小球,CDE是一竖直固定的圆弧形轨道,半径R=0.50
m,OC与竖直方向的夹角θ=60°,现将小球拉到A点(保持绳绷直且水平)由静止释放,当它经过B点时绳恰好被拉断,小球平抛后,从圆弧轨道的C点沿切线方向进入轨道,刚好能到达圆弧形轨道的最高点E,重力加速度g取10
m/s2,不计空气阻力,求:
(1)小球到B点时的速度大小;
(2)轻绳所受的最大拉力大小;
(3)小球在圆弧形轨道上运动时克服阻力做的功.
【反思总结】
答案
【例1】B
【针对训练1】A
【例2】μ=H/s
【例3】(1)3
m/s (2)-4
J
【例4】D
【例5】 ACD
【针对训练2】ABC
【达标训练·限时检测】
A
2、(1)
1.8
(2)
2.16
3、(1)3
m/s (2)30
N (3)8
J
