数学人教A版(2019)必修第二册8.3 第2课时 球的表面积与体积(共35张PPT)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.3 第2课时 球的表面积与体积(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 830.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览








文档简介
(共35张PPT)
8.3 简单几何体的表面积与体积
第2课时 球的表面积与体积
课标定位
素养阐释
1.了解球体的表面积与体积公式的推导过程.
2.掌握球体的表面积与体积公式,能用公式解决简单的实际问题.
3.用类比、联系的运动变化思想推导公式,感受数学运算与几何直观的过程,感受球体的表面积与体积公式在生产活动中的数学建模.
自主预习·新知导学
合作探究·释疑解惑
思
想
方
法
随
堂
练
习
自主预习·新知导学
一、球体的表面积与体积公式
【问题思考】
1.古人在计算圆周率时,一般是用割圆术,即用圆的内接或外切正多边形的周长来逼近圆的周长.理论上,只要取得圆内接正多边形的边数越多,圆周率就越精确,直到无穷.这种思想就是朴素的极限思想.运用上述思想能否计算球的表面积与体积?
提示:可以,运用分割、求近似值、再由近似值转化的数学思想方法.
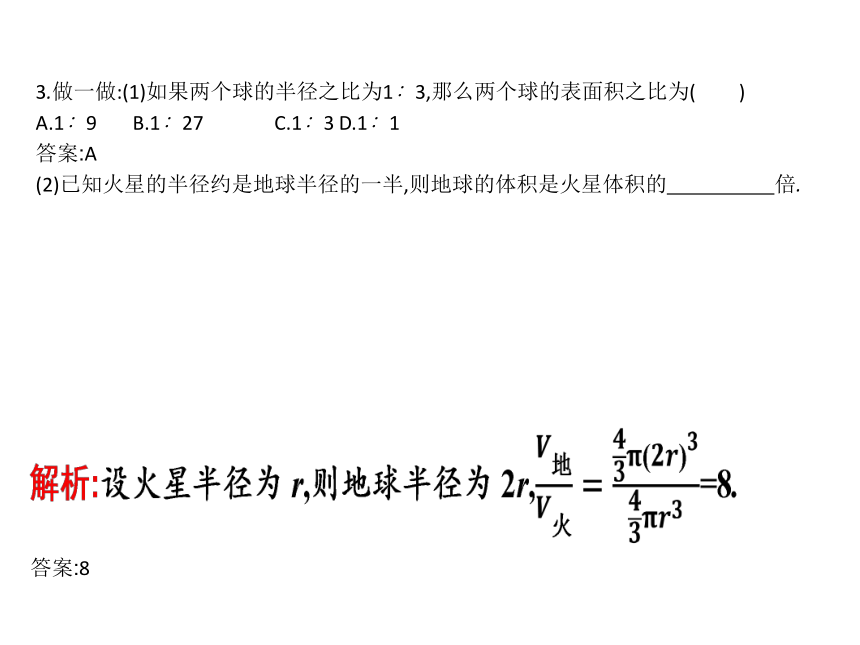
3.做一做:(1)如果两个球的半径之比为1∶3,那么两个球的表面积之比为( )
A.1∶9
B.1∶27
C.1∶3
D.1∶1
答案:A
(2)已知火星的半径约是地球半径的一半,则地球的体积是火星体积的 倍.?
答案:8
(3)已知球的直径为2,求它的表面积和体积.
二、与球有关的计算问题
【问题思考】
1.求球的表面积和体积需要什么条件?
提示:已知球的半径即可.
2.填空:半径与球心是确定球的条件.
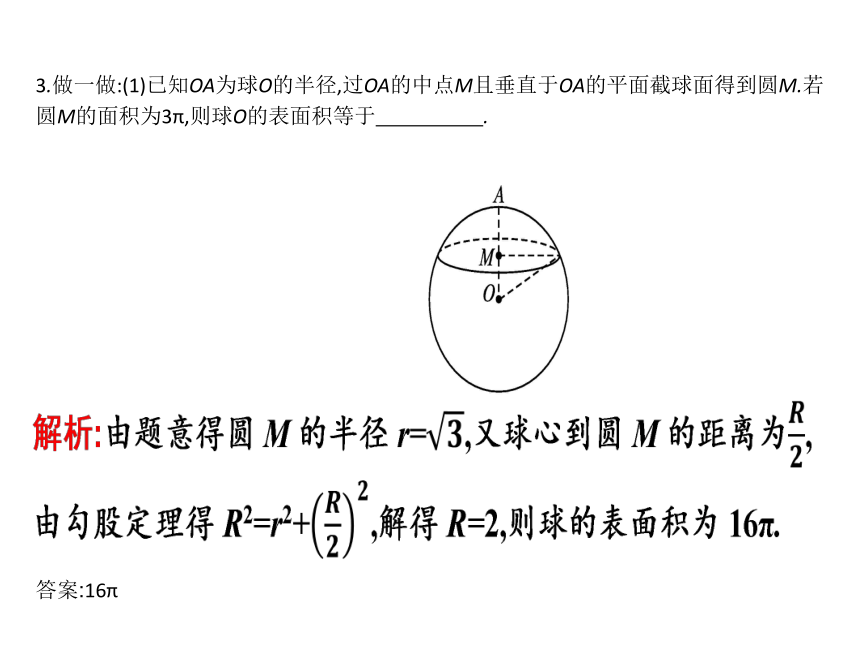
3.做一做:(1)已知OA为球O的半径,过OA的中点M且垂直于OA的平面截球面得到圆M.若圆M的面积为3π,则球O的表面积等于 .?
答案:16π
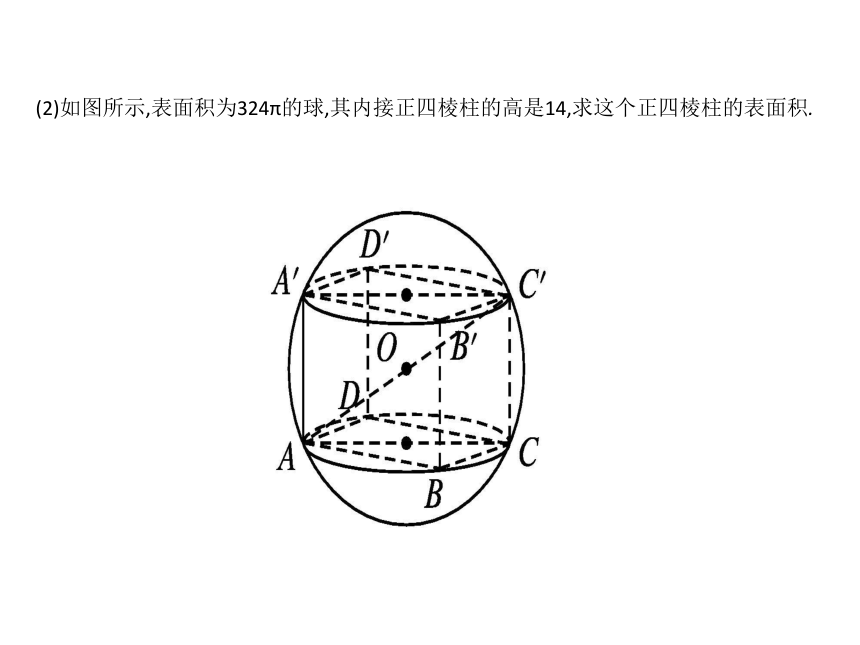
(2)如图所示,表面积为324π的球,其内接正四棱柱的高是14,求这个正四棱柱的表面积.
(3)有一种空心钢球,质量为142
g,测得外径(直径)等于5
cm,求它的内径(钢的密度为7.9
g/cm3,精确到0.1
cm).
(4)在半球内有一个内接正方体,试求这个半球的体积与正方体的体积之比.
解:将半球补成整个的球,同时把原半球的内接正方体再补接一个同样的正方体,构成的长方体刚好是这个球的内接长方体,那么这个长方体的体对角线便是它的外接球的直径.设原正方体的棱长为a,球的半径为R,则根据长方体的对角线性质,得(2R)2=a2+a2+(2a)2,
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)对于一个几何体,若体积一定,则这个几何体是球时表面积最小;反过来,若表面积一定,则这个几何体是球时体积最大.
(
√
)
(2)棱长为a的正方体的外接球的半径为
.(
√
)
(3)正方体的体对角线是它内切球的直径.(
×
)
(4)把球的表面积扩大为原来的2倍,则它的体积扩大为原来的8倍.(
×
)
合作探究·释疑解惑
探究一
探究二
探究一
球体的表面积与体积
【例1】
若圆锥与球的体积相等,且圆锥底面半径与球的直径相等,求圆锥侧面积与球面面积之比.
有关球体的体积与表面积的问题
(1)求球的体积或表面积时,必须知道半径R或者通过条件能求出半径R,然后代入体积或表面积公式求解.
(2)半径和球心是球的最关键要素,把握住了这两点,计算球的表面积或体积的相关题目也就容易了.
(3)球体的体积比等于半径比的立方,表面积比等于半径比的平方.
【变式训练1】
64个直径都为
的球,记它们的体积之和为
V甲,表面积之和为S甲;一个直径为a的球,记其体积为V乙,表面积为S乙,则( )
A.V甲>V乙,且S甲>S乙
B.V甲C.V甲=V乙,且S甲>S乙
D.V甲=V乙,且S甲=S乙
答案:C
探究二
与球有关的切接问题
【例2】
若一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面面积和球的表面积之比为( )
A.4∶3
B.3∶1
C.3∶2
D.9∶4
答案:C
球的内切问题处理的注意事项:
解决与球有关的内切问题主要是指球内切于多面体与旋转体,解答时首先要找准切点,通过作截面来解决.若球内切于多面体,则作截面时主要抓住多面体过球心的对角面来作.
球的外接问题处理的注意事项:
把一个多面体的几个顶点放在球面上即为球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.
【变式训练2】
已知三棱锥A-BCD的外接球为球O,球O的直径是AD,且△ABC,△BCD都是边长为1的等边三角形,则三棱锥A-BCD的体积是( )
答案:A
思
想
方
法
分类与整合思想在球的两平行截面问题中的运用
【典例】
已知球的两平行截面的面积为5π和8π,且相距为1,求这个球的表面积.
解:设以r1为半径的截面面积为5π,以r2为半径的截面面积为8π,O1O2=1,球的半径为R,OO2=x,若球的两平行截面位于球心的同一侧,则可得下列关系式:
即π(R2-x2)-π[R2-(x+1)2]=8π-5π,
即R2-x2-R2+x2+2x+1=3,∴2x=2,即x=1.
∵π(R2-x2)=8π,∴R2-1=8,R2=9,∴R=3.
球的表面积为S=4πR2=4π×32=36π.
若球的两平行截面位于球心的两侧,
则π(R2-x2)-π[R2-(1-x)2]=8π-5π,
即R2-x2-R2+x2-2x+1=3,∴2x=-2,即x=-1.
不符合题意,舍去.
综上,球的表面积为S=4πR2=4π×32=36π.
球的截面问题的解题方法:
(1)有关球的截面问题,常画出过球心的截面圆,将问题转化为平面中圆的问题.
(2)借助球半径R,截面圆半径r,球心到截面的距离d构成的直角三角形,即R2=d2+r2.
(3)两个平行的截面应分清在球心的同侧或异侧.
【变式训练】
已知在球心同侧的两平行截面的面积分别为49π
cm2和400π
cm2,且相距为9
cm,则这个球的表面积为
cm2.?
解析:球的轴截面如图所示,由球的截面性质知,AO1∥BO2,且O1,O2分别为两截面圆的圆心,则OO1⊥AO1,OO2⊥BO2.
设球的半径为R.
∵π·O2B2=49π
cm2,∴O2B=7
cm,
同理π·O1A2=400π
cm2,∴O1A=20
cm.
设OO1=x
cm,则OO2=(x+9)cm.
在Rt△OO1A中,R2=x2+202,
在Rt△OO2B中,R2=(x+9)2+72,
由x2+202=(x+9)2+72,解得x=15,
∴R2=x2+202=252,∴R=25
cm.
∴S球=4πR2=2
500π
cm2.
∴球的表面积为2
500π
cm2.
答案:2
500π
随
堂
练
习
答案:B
答案:C
3.已知三个球的半径之比为1∶2∶3,那么最大球的表面积是其余两个球的表面积之和的( )
解析:根据球的表面积等于其大圆面积的4倍,可设最小的一个半径为r,则另两个半径为2r,3r,所以各球的表面积分别为4πr2,16πr2,36πr2,
答案:C
4.已知棱长为2的正方体的体积与球O的体积相等,则球O的半径为( )
答案:D
5.已知三个球的半径R1,R2,R3满足R1+2R2=3R3,则它们的表面积S1,S2,S3满足的等量关系是 .?
8.3 简单几何体的表面积与体积
第2课时 球的表面积与体积
课标定位
素养阐释
1.了解球体的表面积与体积公式的推导过程.
2.掌握球体的表面积与体积公式,能用公式解决简单的实际问题.
3.用类比、联系的运动变化思想推导公式,感受数学运算与几何直观的过程,感受球体的表面积与体积公式在生产活动中的数学建模.
自主预习·新知导学
合作探究·释疑解惑
思
想
方
法
随
堂
练
习
自主预习·新知导学
一、球体的表面积与体积公式
【问题思考】
1.古人在计算圆周率时,一般是用割圆术,即用圆的内接或外切正多边形的周长来逼近圆的周长.理论上,只要取得圆内接正多边形的边数越多,圆周率就越精确,直到无穷.这种思想就是朴素的极限思想.运用上述思想能否计算球的表面积与体积?
提示:可以,运用分割、求近似值、再由近似值转化的数学思想方法.
3.做一做:(1)如果两个球的半径之比为1∶3,那么两个球的表面积之比为( )
A.1∶9
B.1∶27
C.1∶3
D.1∶1
答案:A
(2)已知火星的半径约是地球半径的一半,则地球的体积是火星体积的 倍.?
答案:8
(3)已知球的直径为2,求它的表面积和体积.
二、与球有关的计算问题
【问题思考】
1.求球的表面积和体积需要什么条件?
提示:已知球的半径即可.
2.填空:半径与球心是确定球的条件.
3.做一做:(1)已知OA为球O的半径,过OA的中点M且垂直于OA的平面截球面得到圆M.若圆M的面积为3π,则球O的表面积等于 .?
答案:16π
(2)如图所示,表面积为324π的球,其内接正四棱柱的高是14,求这个正四棱柱的表面积.
(3)有一种空心钢球,质量为142
g,测得外径(直径)等于5
cm,求它的内径(钢的密度为7.9
g/cm3,精确到0.1
cm).
(4)在半球内有一个内接正方体,试求这个半球的体积与正方体的体积之比.
解:将半球补成整个的球,同时把原半球的内接正方体再补接一个同样的正方体,构成的长方体刚好是这个球的内接长方体,那么这个长方体的体对角线便是它的外接球的直径.设原正方体的棱长为a,球的半径为R,则根据长方体的对角线性质,得(2R)2=a2+a2+(2a)2,
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)对于一个几何体,若体积一定,则这个几何体是球时表面积最小;反过来,若表面积一定,则这个几何体是球时体积最大.
(
√
)
(2)棱长为a的正方体的外接球的半径为
.(
√
)
(3)正方体的体对角线是它内切球的直径.(
×
)
(4)把球的表面积扩大为原来的2倍,则它的体积扩大为原来的8倍.(
×
)
合作探究·释疑解惑
探究一
探究二
探究一
球体的表面积与体积
【例1】
若圆锥与球的体积相等,且圆锥底面半径与球的直径相等,求圆锥侧面积与球面面积之比.
有关球体的体积与表面积的问题
(1)求球的体积或表面积时,必须知道半径R或者通过条件能求出半径R,然后代入体积或表面积公式求解.
(2)半径和球心是球的最关键要素,把握住了这两点,计算球的表面积或体积的相关题目也就容易了.
(3)球体的体积比等于半径比的立方,表面积比等于半径比的平方.
【变式训练1】
64个直径都为
的球,记它们的体积之和为
V甲,表面积之和为S甲;一个直径为a的球,记其体积为V乙,表面积为S乙,则( )
A.V甲>V乙,且S甲>S乙
B.V甲
D.V甲=V乙,且S甲=S乙
答案:C
探究二
与球有关的切接问题
【例2】
若一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面面积和球的表面积之比为( )
A.4∶3
B.3∶1
C.3∶2
D.9∶4
答案:C
球的内切问题处理的注意事项:
解决与球有关的内切问题主要是指球内切于多面体与旋转体,解答时首先要找准切点,通过作截面来解决.若球内切于多面体,则作截面时主要抓住多面体过球心的对角面来作.
球的外接问题处理的注意事项:
把一个多面体的几个顶点放在球面上即为球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.
【变式训练2】
已知三棱锥A-BCD的外接球为球O,球O的直径是AD,且△ABC,△BCD都是边长为1的等边三角形,则三棱锥A-BCD的体积是( )
答案:A
思
想
方
法
分类与整合思想在球的两平行截面问题中的运用
【典例】
已知球的两平行截面的面积为5π和8π,且相距为1,求这个球的表面积.
解:设以r1为半径的截面面积为5π,以r2为半径的截面面积为8π,O1O2=1,球的半径为R,OO2=x,若球的两平行截面位于球心的同一侧,则可得下列关系式:
即π(R2-x2)-π[R2-(x+1)2]=8π-5π,
即R2-x2-R2+x2+2x+1=3,∴2x=2,即x=1.
∵π(R2-x2)=8π,∴R2-1=8,R2=9,∴R=3.
球的表面积为S=4πR2=4π×32=36π.
若球的两平行截面位于球心的两侧,
则π(R2-x2)-π[R2-(1-x)2]=8π-5π,
即R2-x2-R2+x2-2x+1=3,∴2x=-2,即x=-1.
不符合题意,舍去.
综上,球的表面积为S=4πR2=4π×32=36π.
球的截面问题的解题方法:
(1)有关球的截面问题,常画出过球心的截面圆,将问题转化为平面中圆的问题.
(2)借助球半径R,截面圆半径r,球心到截面的距离d构成的直角三角形,即R2=d2+r2.
(3)两个平行的截面应分清在球心的同侧或异侧.
【变式训练】
已知在球心同侧的两平行截面的面积分别为49π
cm2和400π
cm2,且相距为9
cm,则这个球的表面积为
cm2.?
解析:球的轴截面如图所示,由球的截面性质知,AO1∥BO2,且O1,O2分别为两截面圆的圆心,则OO1⊥AO1,OO2⊥BO2.
设球的半径为R.
∵π·O2B2=49π
cm2,∴O2B=7
cm,
同理π·O1A2=400π
cm2,∴O1A=20
cm.
设OO1=x
cm,则OO2=(x+9)cm.
在Rt△OO1A中,R2=x2+202,
在Rt△OO2B中,R2=(x+9)2+72,
由x2+202=(x+9)2+72,解得x=15,
∴R2=x2+202=252,∴R=25
cm.
∴S球=4πR2=2
500π
cm2.
∴球的表面积为2
500π
cm2.
答案:2
500π
随
堂
练
习
答案:B
答案:C
3.已知三个球的半径之比为1∶2∶3,那么最大球的表面积是其余两个球的表面积之和的( )
解析:根据球的表面积等于其大圆面积的4倍,可设最小的一个半径为r,则另两个半径为2r,3r,所以各球的表面积分别为4πr2,16πr2,36πr2,
答案:C
4.已知棱长为2的正方体的体积与球O的体积相等,则球O的半径为( )
答案:D
5.已知三个球的半径R1,R2,R3满足R1+2R2=3R3,则它们的表面积S1,S2,S3满足的等量关系是 .?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
