第二十六章反比例函数复习课件(25张)
文档属性
| 名称 | 第二十六章反比例函数复习课件(25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 513.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 11:02:27 | ||
图片预览







文档简介
反比例函数复习课
第二十六章 反比例函数
1.知识与技能:理解反比例函数、图象及其主要性质,能根据所给信息确定反比例函数表达式,能画出反比例函数的图象,并利用它们解决简单的实际问题,体会函数的应用价值。
2.过程与方法:回顾反比例函数的概念、性质、图象的过程,把数学与实际问题相结合。
3.情感、态度与价值观:进一步了解数学在实际生活中的应用,增强应用意识,体会数学的重要性。
复习目标
1.教学重点:(1)反比例函数的图象和性质;
(2)k的几何意义。
2.教学难点:反比例函数与一次函数的综合应用。
教学重难点
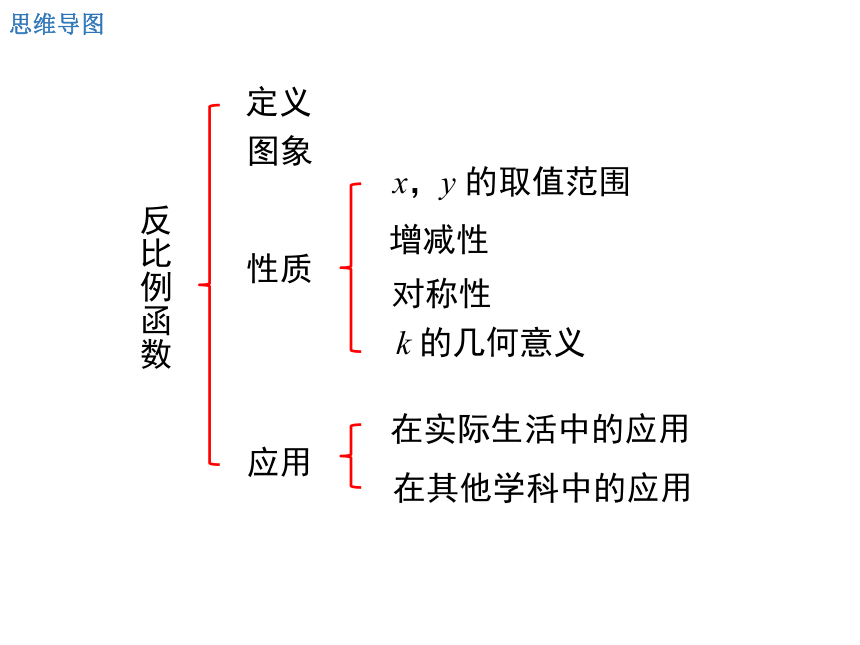
反比例函数
定义
图象
性质
x,y 的取值范围
增减性
对称性
k 的几何意义
应用
在实际生活中的应用
在其他学科中的应用
思维导图
1. 反比例函数的概念
要点梳理
定义:形如________ (k为常数,k≠0) 的函数称为反
比例函数,其中x是自变量,y是x的函数,k是比例
系数.
三种表达式方法: 或 xy=k 或 y=kx-1 (k≠0).
防错提醒:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
2. 反比例函数的图象和性质
(1) 反比例函数的图象:反比例函数 (k≠0)的
图象是 ,它既是 图形又是____
对称图形.
反比例函数的两条对称轴为直线 和 ;
对称中心是: .
双曲线
原点
y = x
y=-x
轴对称
中心
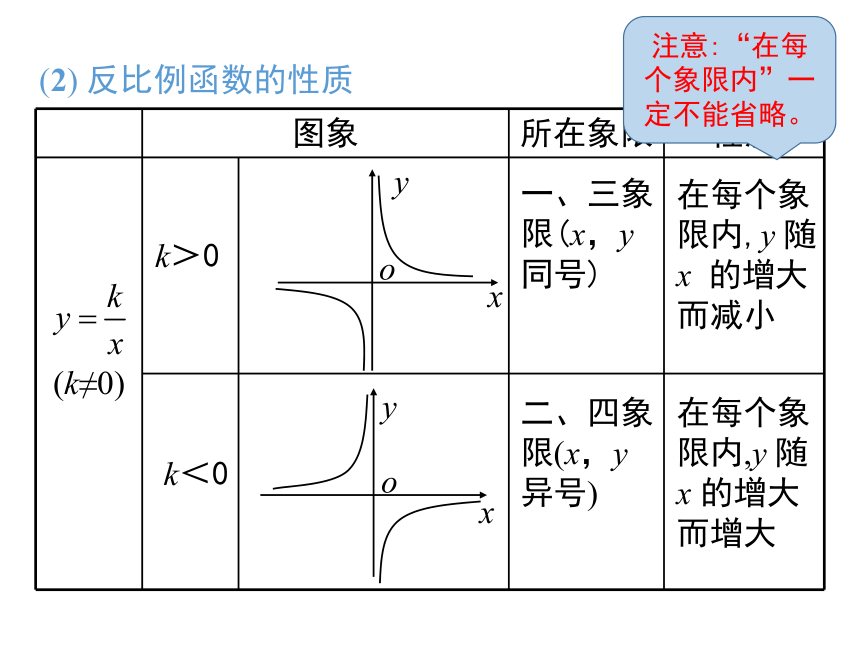
(2) 反比例函数的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
图象
所在象限
性质
(k≠0)
x
y
o
x
y
o
k>0
k<0
一、三象限(x,y同号)
在每个象限内,y 随x 的增大而减小
二、四象限(x,y异号)
在每个象限内,y 随 x 的增大而增大
注意:“在每个象限内”一定不能省略。
填一填
1.函数 是________函数,其图象为________,其中k=___,自变量x的取值范围为_____.
2.函数 的图象位于第_______象限,在每一象限内,y的值随x的增大而______.
当x>0时,y___0,这部分图象位于第____象限.
3.函数 的图象位于第_______象限,在每一象限内,y的值随x的增大而______.
当x>0时,y___0,这部分图象位于第____象限.
反比例
双曲线
2
x≠0
一、三
减小
>
一
二、四
增大
<
四
(3) 反比例函数比例系数 k 的几何意义
k 的几何意义:反比例函数图象上的点 (x,y) 具有
两坐标之积 (xy=k) 为常数这一特点,即过双曲线
上任意一点,向两坐标轴作垂线,两条垂线与坐
标轴所围成的矩形的面积为常数____.
规律:过双曲线上任意一点,向两坐标轴作垂线,
一条垂线与坐标轴、原点所围成的三角形的面积
为常数____.
|k|
3. 反比例函数的应用
?利用待定系数法确定反比例函数:
① 根据两变量之间的反比例关系,设 ;
② 代入图象上一个点的坐标,即 x、y 的一对
对应值;
③ 解出 k 的值;
④ 写出解析式.
归纳:一设 二代 三解 四还原
?反比例函数与一次函数的图象的交点的求法
求直线 y=k1x+b (k1≠0) 和双曲线 (k2≠0)的交点坐标就是解这两个函数解析式组成的方
程组.
?利用反比例函数相关知识解决实际问题
过程:分析实际情境→建立函数模型→明确
数学问题
注意:实际问题中的两个变量往往都只能取
非负值.
考点讲练
考点一 反比例函数的概念
针对训练
1. 下列函数中哪些是反比例函数?
① y = 3x-1
② y = 2x2
⑤ y = 3x
③
④
⑥
⑦
⑧
2. 已知点 P(1,-3) 在反比例函数 的图象上,
则 k 的值是 ( )
A. 3 B. -3
C. D.
B
3. 若 是反比例函数,则 a 的值为 ( )
A. 1 B. -1 C. ±1 D. 任意实数
A
例1 已知点 A(1,y1),B(2,y2),C(-3,y3) 都在反比
例函数 的图象上,则y1,y2,y3的大小关系是
( )
A. y3<y1<y2 B. y1<y2<y3
C. y2<y1<y3 D. y3<y2<y1
解析:方法①分别把各点代入反比例函数求出y1,y2,
y3的值,再比较出其大小即可.
方法②:根据反比例函数的图象和性质比较.
考点二 反比例函数的图象和性质
D
方法总结:比较反比例函数值的大小,在同一个象限内根据反比例函数的性质比较,在不同象限内,不能按其性质比较,函数值的大小只能根据特征确定.
例2 如图,两个反比例函数 和 在第一象
限内的图象分别是 C1 和 C2,设点 P 在 C1 上,PA ⊥
x 轴于点A,交C2于点B,则△POB的面积为 .
1
考点三 与反比例函数 k 有关的问题
针对训练
1. 如图,在平面直角坐标系中,点 M 为 x 轴正半轴 上
一点,过点 M 的直线 l∥ y 轴,且直线 l 分别与反比
例函数 (x>0)和 (x>0) 的图象交于P,Q
两点,若 S△POQ=14,
则 k 的值为 .
-20
4
10
考点四 反比例函数的应用
例3 学校锅炉旁建有一个储煤库,开学时购进一批煤,
现在知道:按每天用煤 0.6 吨计算,一学期 (按150
天计算) 刚好用完. 若每天的耗煤量为 x 吨,那么
这批煤能维持 y 天.
(1) 则 y 与 x 之间有怎样的函数关系?
解:煤的总量为:0.6×150=90 (吨),
根据题意有
(x>0).
(2) 若每天节约 0.1 吨,则这批煤能维持多少天?
∴ 每天的用煤量为 0.6-0.1=0.5 (吨),
解:∵ 每天节约 0.1 吨煤,
∴ 这批煤能维持 180 天.
例4 为了做好校园疫情防控工作,校医每天早上对全校进行药物喷洒消毒,测得药物喷洒后 2 小时,空气中的含药量达到最大值为 4 mg/m3. 已知药物喷洒后,2 小时前每立方米空气中的含药量 y (单位:mg/m3)与时间 x (单位:h) 成正比例函数关系;2 小时后 y 与 x 成反比例函数关系 (如图). 根据以上信息解答下列问题:
O
y(mg/m3)
x/h
2
4
(1) 求当 0 ≤ x ≤2 时,y 与 x 的函数解析式;
解:当 0 ≤ x ≤2 时,
y 与 x 成正比例函数关系.
设 y =k1x,
由于点 (2,4) 在线段上,
所以 4=2k1,k1=2,即 y=2x.
O
y(mg/m3)
x/h
2
4
(2) 求当 x > 2 时,y 与 x 的函数解析式;
解:当 x > 2时,y 与 x 成反比例函数关系,
设 2
解得 k2 =8.
由于点 (2,4) 在反比例函数的图象上,
所以 2
即
O
y(mg/m3)
x/h
2
4
(3) 若每立方米空气的含药量不低于 2 mg时才能有效灭杀病毒,则喷洒一次药物,有效杀毒的时间是多长?
O
y(mg/m3)
x/h
2
4
2
解:∵当 0≤x≤2 时,当y=2时,代入y=2x,
∴解得x=1,
∵当x≥2时,当y=2时,代入 y= ,
∴解得x=4,
∴有效杀毒的时间是4-1=3(小时).
4
1
课堂小结
1.通过今天的学习,你的收获是什么?
2.你还有什么疑问?
课后作业:
中考总复习P61—64:反比例函数的图像与性质
第二十六章 反比例函数
1.知识与技能:理解反比例函数、图象及其主要性质,能根据所给信息确定反比例函数表达式,能画出反比例函数的图象,并利用它们解决简单的实际问题,体会函数的应用价值。
2.过程与方法:回顾反比例函数的概念、性质、图象的过程,把数学与实际问题相结合。
3.情感、态度与价值观:进一步了解数学在实际生活中的应用,增强应用意识,体会数学的重要性。
复习目标
1.教学重点:(1)反比例函数的图象和性质;
(2)k的几何意义。
2.教学难点:反比例函数与一次函数的综合应用。
教学重难点
反比例函数
定义
图象
性质
x,y 的取值范围
增减性
对称性
k 的几何意义
应用
在实际生活中的应用
在其他学科中的应用
思维导图
1. 反比例函数的概念
要点梳理
定义:形如________ (k为常数,k≠0) 的函数称为反
比例函数,其中x是自变量,y是x的函数,k是比例
系数.
三种表达式方法: 或 xy=k 或 y=kx-1 (k≠0).
防错提醒:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
2. 反比例函数的图象和性质
(1) 反比例函数的图象:反比例函数 (k≠0)的
图象是 ,它既是 图形又是____
对称图形.
反比例函数的两条对称轴为直线 和 ;
对称中心是: .
双曲线
原点
y = x
y=-x
轴对称
中心
(2) 反比例函数的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
图象
所在象限
性质
(k≠0)
x
y
o
x
y
o
k>0
k<0
一、三象限(x,y同号)
在每个象限内,y 随x 的增大而减小
二、四象限(x,y异号)
在每个象限内,y 随 x 的增大而增大
注意:“在每个象限内”一定不能省略。
填一填
1.函数 是________函数,其图象为________,其中k=___,自变量x的取值范围为_____.
2.函数 的图象位于第_______象限,在每一象限内,y的值随x的增大而______.
当x>0时,y___0,这部分图象位于第____象限.
3.函数 的图象位于第_______象限,在每一象限内,y的值随x的增大而______.
当x>0时,y___0,这部分图象位于第____象限.
反比例
双曲线
2
x≠0
一、三
减小
>
一
二、四
增大
<
四
(3) 反比例函数比例系数 k 的几何意义
k 的几何意义:反比例函数图象上的点 (x,y) 具有
两坐标之积 (xy=k) 为常数这一特点,即过双曲线
上任意一点,向两坐标轴作垂线,两条垂线与坐
标轴所围成的矩形的面积为常数____.
规律:过双曲线上任意一点,向两坐标轴作垂线,
一条垂线与坐标轴、原点所围成的三角形的面积
为常数____.
|k|
3. 反比例函数的应用
?利用待定系数法确定反比例函数:
① 根据两变量之间的反比例关系,设 ;
② 代入图象上一个点的坐标,即 x、y 的一对
对应值;
③ 解出 k 的值;
④ 写出解析式.
归纳:一设 二代 三解 四还原
?反比例函数与一次函数的图象的交点的求法
求直线 y=k1x+b (k1≠0) 和双曲线 (k2≠0)的交点坐标就是解这两个函数解析式组成的方
程组.
?利用反比例函数相关知识解决实际问题
过程:分析实际情境→建立函数模型→明确
数学问题
注意:实际问题中的两个变量往往都只能取
非负值.
考点讲练
考点一 反比例函数的概念
针对训练
1. 下列函数中哪些是反比例函数?
① y = 3x-1
② y = 2x2
⑤ y = 3x
③
④
⑥
⑦
⑧
2. 已知点 P(1,-3) 在反比例函数 的图象上,
则 k 的值是 ( )
A. 3 B. -3
C. D.
B
3. 若 是反比例函数,则 a 的值为 ( )
A. 1 B. -1 C. ±1 D. 任意实数
A
例1 已知点 A(1,y1),B(2,y2),C(-3,y3) 都在反比
例函数 的图象上,则y1,y2,y3的大小关系是
( )
A. y3<y1<y2 B. y1<y2<y3
C. y2<y1<y3 D. y3<y2<y1
解析:方法①分别把各点代入反比例函数求出y1,y2,
y3的值,再比较出其大小即可.
方法②:根据反比例函数的图象和性质比较.
考点二 反比例函数的图象和性质
D
方法总结:比较反比例函数值的大小,在同一个象限内根据反比例函数的性质比较,在不同象限内,不能按其性质比较,函数值的大小只能根据特征确定.
例2 如图,两个反比例函数 和 在第一象
限内的图象分别是 C1 和 C2,设点 P 在 C1 上,PA ⊥
x 轴于点A,交C2于点B,则△POB的面积为 .
1
考点三 与反比例函数 k 有关的问题
针对训练
1. 如图,在平面直角坐标系中,点 M 为 x 轴正半轴 上
一点,过点 M 的直线 l∥ y 轴,且直线 l 分别与反比
例函数 (x>0)和 (x>0) 的图象交于P,Q
两点,若 S△POQ=14,
则 k 的值为 .
-20
4
10
考点四 反比例函数的应用
例3 学校锅炉旁建有一个储煤库,开学时购进一批煤,
现在知道:按每天用煤 0.6 吨计算,一学期 (按150
天计算) 刚好用完. 若每天的耗煤量为 x 吨,那么
这批煤能维持 y 天.
(1) 则 y 与 x 之间有怎样的函数关系?
解:煤的总量为:0.6×150=90 (吨),
根据题意有
(x>0).
(2) 若每天节约 0.1 吨,则这批煤能维持多少天?
∴ 每天的用煤量为 0.6-0.1=0.5 (吨),
解:∵ 每天节约 0.1 吨煤,
∴ 这批煤能维持 180 天.
例4 为了做好校园疫情防控工作,校医每天早上对全校进行药物喷洒消毒,测得药物喷洒后 2 小时,空气中的含药量达到最大值为 4 mg/m3. 已知药物喷洒后,2 小时前每立方米空气中的含药量 y (单位:mg/m3)与时间 x (单位:h) 成正比例函数关系;2 小时后 y 与 x 成反比例函数关系 (如图). 根据以上信息解答下列问题:
O
y(mg/m3)
x/h
2
4
(1) 求当 0 ≤ x ≤2 时,y 与 x 的函数解析式;
解:当 0 ≤ x ≤2 时,
y 与 x 成正比例函数关系.
设 y =k1x,
由于点 (2,4) 在线段上,
所以 4=2k1,k1=2,即 y=2x.
O
y(mg/m3)
x/h
2
4
(2) 求当 x > 2 时,y 与 x 的函数解析式;
解:当 x > 2时,y 与 x 成反比例函数关系,
设 2
解得 k2 =8.
由于点 (2,4) 在反比例函数的图象上,
所以 2
即
O
y(mg/m3)
x/h
2
4
(3) 若每立方米空气的含药量不低于 2 mg时才能有效灭杀病毒,则喷洒一次药物,有效杀毒的时间是多长?
O
y(mg/m3)
x/h
2
4
2
解:∵当 0≤x≤2 时,当y=2时,代入y=2x,
∴解得x=1,
∵当x≥2时,当y=2时,代入 y= ,
∴解得x=4,
∴有效杀毒的时间是4-1=3(小时).
4
1
课堂小结
1.通过今天的学习,你的收获是什么?
2.你还有什么疑问?
课后作业:
中考总复习P61—64:反比例函数的图像与性质
