六年级下册数学课件 2.5 正比例 北京版(19张ppt)
文档属性
| 名称 | 六年级下册数学课件 2.5 正比例 北京版(19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 09:26:28 | ||
图片预览






文档简介
六年级数学下册第四单元第二节
正比例
1.正方形的周长与边长、面积与边长是不是相关联的量?
2.如果正方形的边长增加时,周长会增加吗?面积也会增加吗?
知识链接 复习导入
学习目标
1.结合“正方形的周长与边长,正方形的面积与边长,路程、时间与速度”等情境,经历正比例意义的建构过程,能从变化中看到“不变”,认识正比例。
2.正确认识正比例的意义。(重点)
3.能根据正比例的意义,判断两个相关联的量是不是成正比例。(难点)
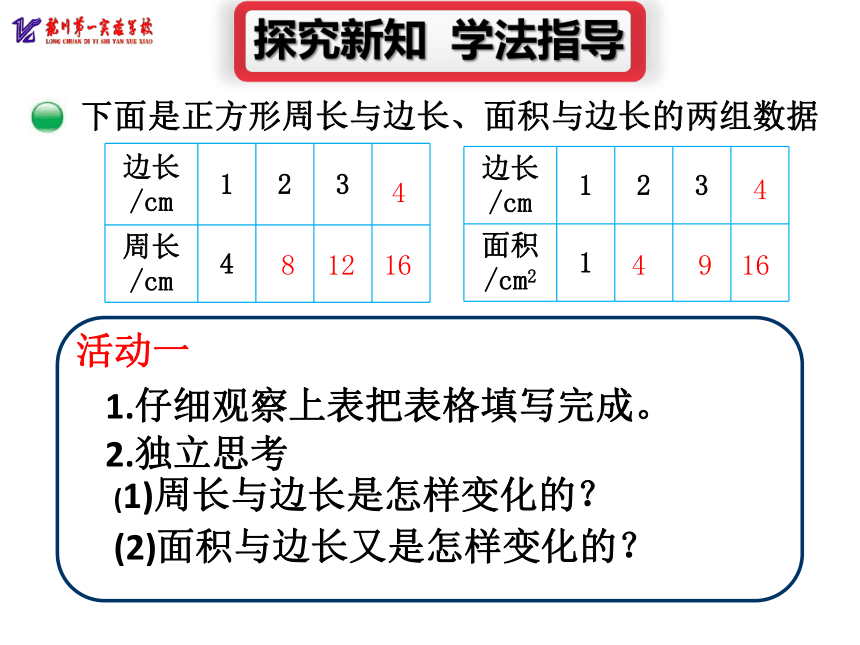
下面是正方形周长与边长、面积与边长的两组数据
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
周长/cm
4
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
面积/cm2
1
活动一
1.仔细观察上表把表格填写完成。
2.独立思考
(1)周长与边长是怎样变化的?
(2)面积与边长又是怎样变化的?
8
12
4
16
4
9
4
16
探究新知 学法指导
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
周长/cm
4
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
面积/cm2
1
12
8
4
16
4
4
9
16
小组合作 成果展示
小组讨论一
正方形的周长与边长的变化规律和面积与边长的变化规律相同吗?并说明理由
一辆汽车行驶的速度为90千米/时,汽车行驶的时间与路程如下表
时间(时)
路程(千米)
1
2
3
4
5
6
7
8
90
180
270
360
…
…
450
540
630
720
活动二
1.仔细观察上表把表格填写完成。
2.在行驶问题中,有路程、时间、还有( )
3.你完成上表数据依据是什么?
一辆汽车行驶的速度为90千米/时,汽车行驶的时间与路程如下表
时间(时)
路程(千米)
1
2
3
4
5
6
7
8
90
180
270
360
…
…
450
540
630
720
小组讨论二
(1)上表中哪两种量是变化的量?哪一种量是不变的量?
(2)寻找路程与时间之间的变化规律?
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么?
{5940675A-B579-460E-94D1-54222C63F5DA}时间/时
1
2
3
4
5
6
7
路程/km
90
180
270
360
450
540
630
8
720
像这样,路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
如果用x和y表示两种相关联的量,用k表示它们的比值,那么上面这种数量关系式可以怎样写呢??
y
x
=k
(一定)来表示。
?可以用
如何判断两种量是否成正比例?
(2)它们的比值(商) 一定。
(1)是两种相关联的量。
这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
判断正方形周长与边长、面积与边长是否成正比例?
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
4
周长/cm
4
8
12
16
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
4
面积/cm2
1
4
9
16
你敢挑战吗?每个卡通后面都有一道题,你想挑战哪一个?
1.一种笔记本,数量与总价如下表:
(1)把上面的表格填写完整。
(2)表中有( )和( )两种量,( )变化,( )也随着变化。
(3)写出表中两种相对应 的量的比值,说说你有什么发现。
(4)总价与数量这两种量是否成正比例?
课堂检测 学习反思
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}数量/本
1
2
3
4
总价/元
3
6
9
15
2.判断下面两种量是不是成正比例,说明理由。
(1)圆柱的底面积一定,体积和高。
(2)工作效率一定,工作时间和工作总量。
(3)和一定,加数和另一个加数。
(4)苹果总数一定,吃掉的苹果个数和未吃的苹果个数
成正比例
不成正比例
不成正比例
成正比例
这堂课你有什么收获?
知识小结 巩固升华
1.认识正比例的意义。
2.判断正比例的条件。
同学们通过观察举一个生活中正比例的例子,下课后跟自己的同桌说一说。
已知a和b成正比例,完成下表。
a
30
50
65
1.5
b
6
3
8
0.5
15
0.3
13
40
2.5
10
知识迁移 课后作业
正比例
1.正方形的周长与边长、面积与边长是不是相关联的量?
2.如果正方形的边长增加时,周长会增加吗?面积也会增加吗?
知识链接 复习导入
学习目标
1.结合“正方形的周长与边长,正方形的面积与边长,路程、时间与速度”等情境,经历正比例意义的建构过程,能从变化中看到“不变”,认识正比例。
2.正确认识正比例的意义。(重点)
3.能根据正比例的意义,判断两个相关联的量是不是成正比例。(难点)
下面是正方形周长与边长、面积与边长的两组数据
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
周长/cm
4
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
面积/cm2
1
活动一
1.仔细观察上表把表格填写完成。
2.独立思考
(1)周长与边长是怎样变化的?
(2)面积与边长又是怎样变化的?
8
12
4
16
4
9
4
16
探究新知 学法指导
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
周长/cm
4
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
面积/cm2
1
12
8
4
16
4
4
9
16
小组合作 成果展示
小组讨论一
正方形的周长与边长的变化规律和面积与边长的变化规律相同吗?并说明理由
一辆汽车行驶的速度为90千米/时,汽车行驶的时间与路程如下表
时间(时)
路程(千米)
1
2
3
4
5
6
7
8
90
180
270
360
…
…
450
540
630
720
活动二
1.仔细观察上表把表格填写完成。
2.在行驶问题中,有路程、时间、还有( )
3.你完成上表数据依据是什么?
一辆汽车行驶的速度为90千米/时,汽车行驶的时间与路程如下表
时间(时)
路程(千米)
1
2
3
4
5
6
7
8
90
180
270
360
…
…
450
540
630
720
小组讨论二
(1)上表中哪两种量是变化的量?哪一种量是不变的量?
(2)寻找路程与时间之间的变化规律?
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么?
{5940675A-B579-460E-94D1-54222C63F5DA}时间/时
1
2
3
4
5
6
7
路程/km
90
180
270
360
450
540
630
8
720
像这样,路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
如果用x和y表示两种相关联的量,用k表示它们的比值,那么上面这种数量关系式可以怎样写呢??
y
x
=k
(一定)来表示。
?可以用
如何判断两种量是否成正比例?
(2)它们的比值(商) 一定。
(1)是两种相关联的量。
这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
判断正方形周长与边长、面积与边长是否成正比例?
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
4
周长/cm
4
8
12
16
{5940675A-B579-460E-94D1-54222C63F5DA}边长/cm
1
2
3
4
面积/cm2
1
4
9
16
你敢挑战吗?每个卡通后面都有一道题,你想挑战哪一个?
1.一种笔记本,数量与总价如下表:
(1)把上面的表格填写完整。
(2)表中有( )和( )两种量,( )变化,( )也随着变化。
(3)写出表中两种相对应 的量的比值,说说你有什么发现。
(4)总价与数量这两种量是否成正比例?
课堂检测 学习反思
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}数量/本
1
2
3
4
总价/元
3
6
9
15
2.判断下面两种量是不是成正比例,说明理由。
(1)圆柱的底面积一定,体积和高。
(2)工作效率一定,工作时间和工作总量。
(3)和一定,加数和另一个加数。
(4)苹果总数一定,吃掉的苹果个数和未吃的苹果个数
成正比例
不成正比例
不成正比例
成正比例
这堂课你有什么收获?
知识小结 巩固升华
1.认识正比例的意义。
2.判断正比例的条件。
同学们通过观察举一个生活中正比例的例子,下课后跟自己的同桌说一说。
已知a和b成正比例,完成下表。
a
30
50
65
1.5
b
6
3
8
0.5
15
0.3
13
40
2.5
10
知识迁移 课后作业
