2021年人教版八年级数学下册“清明节”假期作业训练题(四)(Word版 含解析 )
文档属性
| 名称 | 2021年人教版八年级数学下册“清明节”假期作业训练题(四)(Word版 含解析 ) |  | |
| 格式 | doc | ||
| 文件大小 | 208.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 14:11:21 | ||
图片预览



文档简介
2021年人教版八年级数学下册“清明节”假期作业训练题(四)
第18章《平行四边形》几何解答题(基础)训练
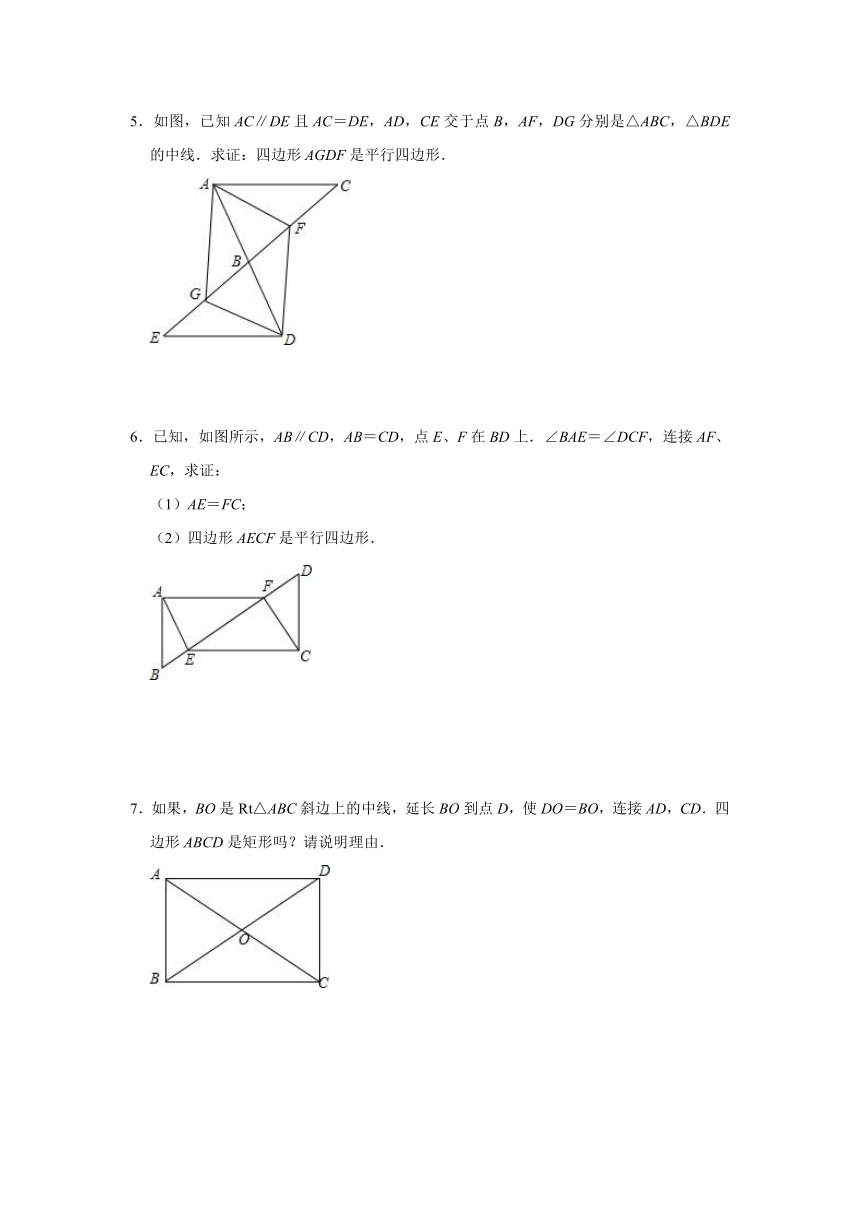
1.如图,在?ABCD中,点E,F分别在边BC,AD上,且AF=CE.求证:四边形AECF是平行四边形.
2.如图,在平行四边形ABCD中,BE交对角线AC于点E,DF∥BE交AC于点F,求证:BE=DF.
3.如图,?OABC的顶点O、A、C的坐标分别为(0,0)、(a,0)、(b,c),求顶点B的坐标.
4.如图,在?ABCD中,E,F分别是AB、BC的中点,O是对角线的交点,若OE=4cm,OF=3cm,求?ABCD的周长.
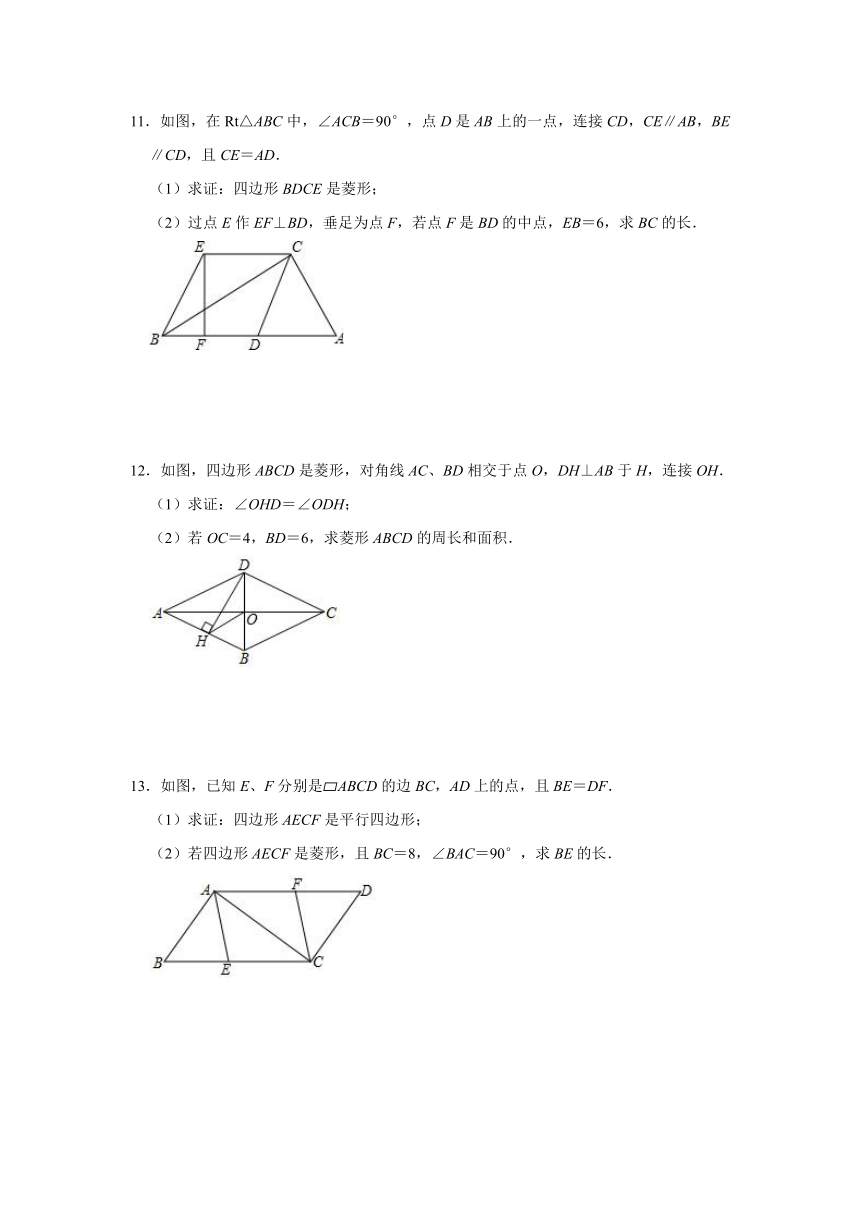
5.如图,已知AC∥DE且AC=DE,AD,CE交于点B,AF,DG分别是△ABC,△BDE的中线.求证:四边形AGDF是平行四边形.
6.已知,如图所示,AB∥CD,AB=CD,点E、F在BD上.∠BAE=∠DCF,连接AF、EC,求证:
(1)AE=FC;
(2)四边形AECF是平行四边形.
7.如果,BO是Rt△ABC斜边上的中线,延长BO到点D,使DO=BO,连接AD,CD.四边形ABCD是矩形吗?请说明理由.
8.如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形ADFE是矩形;
(2)连接OF,若AD=6,EC=4,∠ABF=60°,求OF的长度.
9.如图,已知菱形ABCD的对角线AC、BD相交于点O,分别过A、D两点作AO、DO的垂线,两垂线交于点E.
(1)求证:四边形AODE是矩形;
(2)若四边形AODE的面积为12,AD=5,求四边形AODE的周长.
10.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD.
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.
11.如图,在Rt△ABC中,∠ACB=90°,点D是AB上的一点,连接CD,CE∥AB,BE∥CD,且CE=AD.
(1)求证:四边形BDCE是菱形;
(2)过点E作EF⊥BD,垂足为点F,若点F是BD的中点,EB=6,求BC的长.
12.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH.
(1)求证:∠OHD=∠ODH;
(2)若OC=4,BD=6,求菱形ABCD的周长和面积.
13.如图,已知E、F分别是?ABCD的边BC,AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=8,∠BAC=90°,求BE的长.
14.如图,四边形ABCD是正方形,对角线AC、BD相交于点F,∠E=90°,ED=EC.求证:四边形DFCE是正方形.
15.如图,E为正方形ABCD的边AB延长线上一点,DE交AC于点F,交BC于点G,H为GE的中点,求证:FB⊥BH.
16.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
参考答案
1.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AF=CE,
∴四边形AECF是平行四边形.
2.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠BCE.
又∵DF∥BE
∴∠AFD=∠CEB,
在△AFD和△CEB中,
∴△AFD≌△CEB(AAS),
∴BE=DF.
3.解:过C作CD⊥OA,
在?OABC中,O(0,0),A(a,0),
∴OA=a.
又∵BC∥AO,
∴点B的纵坐标与点C的纵坐标相等,
∴B(a+b,c).
4.解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AB=CD,AD=BC,
∵E,F分别是AB、BC的中点,
∴BC=2EO,CD=2FO,
∵OE=4cm,OF=3cm,
∴BC=8cm,DC=6cm,
∴AD=8cm,AB=6cm,
∴?ABCD的周长为6+6+8+8=28(cm).
5.证明:∵AC∥DE,
∴∠C=∠E,
在△ABC和△DBE中,
,
∴△ABC≌△DBE(AAS),
∴CB=EB,AB=DB,
∵AF,DG分别是△ABC,△BDE的中线,
∴BF=BC,GB=BE,
∴GB=FB,
∴四边形AGDF是平行四边形.
6.证明:(1)∵AB∥CD,
∴∠B=∠D.
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA).
∴AE=CF.
(2)由(1)△ABE≌△CDF得AE=CF,∠AEB=∠CFD,
∴180°﹣∠AEB=180°﹣∠CFD,
即∠AEF=∠CFE.
∴AE∥CF.
∵AE=CF,
∴四边形AECF是平行四边形.
7.解:四边形ABCD是矩形.
理由:∵BO是Rt△ABC斜边上的中线,
∴OA=OC=OB,
∵DO=BO,
∴四边形ABCD是平行四边形,且AC=BD,
∴四边形ABCD是矩形.
8.(1)证明:∵在平行四边形ABCD中,
∴AB∥DC且AB=DC,
∴∠ABE=∠DCF,
在△ABE和△DCF中,,
∴△ABE≌△DCF(SAS),
∴AE=DF,∠AEB=∠DFC=90°,
∴AE∥DF,
∴四边形ADFE是矩形;
(2)解:由(1)知:四边形ADFE是矩形,
∴EF=AD=6,
∵EC=4,
∴BE=CF=2,
∴BF=8,
Rt△ABE中,∠ABE=60°,
∴AB=2BE=4,
∴DF=AE=,
∴BD==2,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OF=BD=.
9.(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,
∵EA⊥AO,DE⊥DO,
∴∠EAO=∠DOA=90°,
∴四边形AODE是矩形;
(2)解:由(1)知,四边形AODE是矩形,
∴∠AED=90°,OA=DE,OD=AE,
∵四边形AODE的面积为12,
∴OA?OD=12,
在Rt△AOD中,根据勾股定理,得OA2+OD2=AD2=25,
∴(OA+OD)2=OA2+2OA?OD+OD2=25+24=49,
∴OA+OD=7,
∴四边形AODE的周长为2(OA+OD)=14.
10.解:(1)∵AC、BD分别是∠BAD、∠ABC的平分线,
∴∠DAC=∠BAC,∠ABD=∠DBC,
∵AE∥BF,
∴∠DAB+∠CBA,=180°,
∴∠BAC+∠ABD=(∠DAB+∠ABC)=×180°=90°,
∴∠AOD=90°;
(2)证明:∵AE∥BF,
∴∠ADB=∠DBC,∠DAC=∠BCA,
∵AC、BD分别是∠BAD、∠ABC的平分线,
∴∠DAC=∠BAC,∠ABD=∠DBC,
∴∠BAC=∠ACB,∠ABD=∠ADB,
∴AB=BC,AB=AD
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴四边形ABCD是菱形.
11.(1)证明:∵CE∥AB,BE∥CD,
∴四边形BDCE是平行四边形,
∴CE=BD,
∵CE=AD,
∴BD=AD,
又∵∠ACB=90°,
∴CD=AB=BD,
∴四边形BDCE是菱形;
(2)解:连接DE,如图所示:
由(1)得:四边形BDCE是菱形,
∴BC⊥DE,BD=BE,OB=OC,
∵EF⊥BD,点F是BD的中点,
∴BE=DE,
∴BE=DE=BD,
∴∠DBE=60°,∠EBC=∠EBD=30°,
∴OE=EB=3,
∴OB===3,
∴BC=2OB=6.
12.(1)证明:∵四边形ABCD是菱形,
∴OD=OB,AB∥CD,BD⊥AC,
∵DH⊥AB,
∴∠DHB=90°,
∴OH=BD=OD,
∴∠OHD=∠ODH;
(2)∵四边形ABCD是菱形,
∴OD=OB=BD=3,OA=OC=4,BD⊥AC,
在 Rt△OCD中,CD==5,
∴菱形ABCD的周长=4CD=20,
菱形ABCD的面积=×6×8=24.
13.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴AF∥EC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形;
(2)∵四边形AECF是菱形,
∴AE=EC,
∴∠1=∠2,
∵∠BAC=90°,
∴∠3=90°﹣∠2,∠4=90°﹣∠1,
∴∠3=∠4,
∴AE=BE,
∴BE=AE=CE=BC=4.
14.解:∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°,
∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,
∵DE=CE,
∴四边形DFCE是正方形.
15.证明:如图,∵ABCD为正方形,
∴DC=CB,∠DCB=90°,∠DCF=∠BCF=45°,
在△DFC与△BFC中,
,
∴△DFC≌△BFC(SAS),
∴∠1=∠6,
∵BH为中线,
∴BH=GH,
∴∠3=∠4,
∵∠4=∠5,∠5+∠6=90°,
∴∠1+∠3=90°,
即BF⊥CH.
16.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵四边形ABEF是正方形,
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∵AD=AE,
∴AD﹣AF=AE﹣AG,
即DF=EG,
在△DFO和△EGO中,,
∴△DFO≌△EGO(AAS),
∴FO=GO,FD=EG
∵∠DAE=∠AEF=45°,∠AFE=∠AGD=90°,
∴DF=FO=OG=EG,
∴DO=OF=OG,
∴DG=DO+OG=OG+OG=1,
∴OG==﹣1,
∴OD=(﹣1)=2﹣.
第18章《平行四边形》几何解答题(基础)训练
1.如图,在?ABCD中,点E,F分别在边BC,AD上,且AF=CE.求证:四边形AECF是平行四边形.
2.如图,在平行四边形ABCD中,BE交对角线AC于点E,DF∥BE交AC于点F,求证:BE=DF.
3.如图,?OABC的顶点O、A、C的坐标分别为(0,0)、(a,0)、(b,c),求顶点B的坐标.
4.如图,在?ABCD中,E,F分别是AB、BC的中点,O是对角线的交点,若OE=4cm,OF=3cm,求?ABCD的周长.
5.如图,已知AC∥DE且AC=DE,AD,CE交于点B,AF,DG分别是△ABC,△BDE的中线.求证:四边形AGDF是平行四边形.
6.已知,如图所示,AB∥CD,AB=CD,点E、F在BD上.∠BAE=∠DCF,连接AF、EC,求证:
(1)AE=FC;
(2)四边形AECF是平行四边形.
7.如果,BO是Rt△ABC斜边上的中线,延长BO到点D,使DO=BO,连接AD,CD.四边形ABCD是矩形吗?请说明理由.
8.如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形ADFE是矩形;
(2)连接OF,若AD=6,EC=4,∠ABF=60°,求OF的长度.
9.如图,已知菱形ABCD的对角线AC、BD相交于点O,分别过A、D两点作AO、DO的垂线,两垂线交于点E.
(1)求证:四边形AODE是矩形;
(2)若四边形AODE的面积为12,AD=5,求四边形AODE的周长.
10.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD.
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.
11.如图,在Rt△ABC中,∠ACB=90°,点D是AB上的一点,连接CD,CE∥AB,BE∥CD,且CE=AD.
(1)求证:四边形BDCE是菱形;
(2)过点E作EF⊥BD,垂足为点F,若点F是BD的中点,EB=6,求BC的长.
12.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH.
(1)求证:∠OHD=∠ODH;
(2)若OC=4,BD=6,求菱形ABCD的周长和面积.
13.如图,已知E、F分别是?ABCD的边BC,AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=8,∠BAC=90°,求BE的长.
14.如图,四边形ABCD是正方形,对角线AC、BD相交于点F,∠E=90°,ED=EC.求证:四边形DFCE是正方形.
15.如图,E为正方形ABCD的边AB延长线上一点,DE交AC于点F,交BC于点G,H为GE的中点,求证:FB⊥BH.
16.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OD的长.
参考答案
1.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AF=CE,
∴四边形AECF是平行四边形.
2.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠BCE.
又∵DF∥BE
∴∠AFD=∠CEB,
在△AFD和△CEB中,
∴△AFD≌△CEB(AAS),
∴BE=DF.
3.解:过C作CD⊥OA,
在?OABC中,O(0,0),A(a,0),
∴OA=a.
又∵BC∥AO,
∴点B的纵坐标与点C的纵坐标相等,
∴B(a+b,c).
4.解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AB=CD,AD=BC,
∵E,F分别是AB、BC的中点,
∴BC=2EO,CD=2FO,
∵OE=4cm,OF=3cm,
∴BC=8cm,DC=6cm,
∴AD=8cm,AB=6cm,
∴?ABCD的周长为6+6+8+8=28(cm).
5.证明:∵AC∥DE,
∴∠C=∠E,
在△ABC和△DBE中,
,
∴△ABC≌△DBE(AAS),
∴CB=EB,AB=DB,
∵AF,DG分别是△ABC,△BDE的中线,
∴BF=BC,GB=BE,
∴GB=FB,
∴四边形AGDF是平行四边形.
6.证明:(1)∵AB∥CD,
∴∠B=∠D.
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA).
∴AE=CF.
(2)由(1)△ABE≌△CDF得AE=CF,∠AEB=∠CFD,
∴180°﹣∠AEB=180°﹣∠CFD,
即∠AEF=∠CFE.
∴AE∥CF.
∵AE=CF,
∴四边形AECF是平行四边形.
7.解:四边形ABCD是矩形.
理由:∵BO是Rt△ABC斜边上的中线,
∴OA=OC=OB,
∵DO=BO,
∴四边形ABCD是平行四边形,且AC=BD,
∴四边形ABCD是矩形.
8.(1)证明:∵在平行四边形ABCD中,
∴AB∥DC且AB=DC,
∴∠ABE=∠DCF,
在△ABE和△DCF中,,
∴△ABE≌△DCF(SAS),
∴AE=DF,∠AEB=∠DFC=90°,
∴AE∥DF,
∴四边形ADFE是矩形;
(2)解:由(1)知:四边形ADFE是矩形,
∴EF=AD=6,
∵EC=4,
∴BE=CF=2,
∴BF=8,
Rt△ABE中,∠ABE=60°,
∴AB=2BE=4,
∴DF=AE=,
∴BD==2,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OF=BD=.
9.(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,
∵EA⊥AO,DE⊥DO,
∴∠EAO=∠DOA=90°,
∴四边形AODE是矩形;
(2)解:由(1)知,四边形AODE是矩形,
∴∠AED=90°,OA=DE,OD=AE,
∵四边形AODE的面积为12,
∴OA?OD=12,
在Rt△AOD中,根据勾股定理,得OA2+OD2=AD2=25,
∴(OA+OD)2=OA2+2OA?OD+OD2=25+24=49,
∴OA+OD=7,
∴四边形AODE的周长为2(OA+OD)=14.
10.解:(1)∵AC、BD分别是∠BAD、∠ABC的平分线,
∴∠DAC=∠BAC,∠ABD=∠DBC,
∵AE∥BF,
∴∠DAB+∠CBA,=180°,
∴∠BAC+∠ABD=(∠DAB+∠ABC)=×180°=90°,
∴∠AOD=90°;
(2)证明:∵AE∥BF,
∴∠ADB=∠DBC,∠DAC=∠BCA,
∵AC、BD分别是∠BAD、∠ABC的平分线,
∴∠DAC=∠BAC,∠ABD=∠DBC,
∴∠BAC=∠ACB,∠ABD=∠ADB,
∴AB=BC,AB=AD
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴四边形ABCD是菱形.
11.(1)证明:∵CE∥AB,BE∥CD,
∴四边形BDCE是平行四边形,
∴CE=BD,
∵CE=AD,
∴BD=AD,
又∵∠ACB=90°,
∴CD=AB=BD,
∴四边形BDCE是菱形;
(2)解:连接DE,如图所示:
由(1)得:四边形BDCE是菱形,
∴BC⊥DE,BD=BE,OB=OC,
∵EF⊥BD,点F是BD的中点,
∴BE=DE,
∴BE=DE=BD,
∴∠DBE=60°,∠EBC=∠EBD=30°,
∴OE=EB=3,
∴OB===3,
∴BC=2OB=6.
12.(1)证明:∵四边形ABCD是菱形,
∴OD=OB,AB∥CD,BD⊥AC,
∵DH⊥AB,
∴∠DHB=90°,
∴OH=BD=OD,
∴∠OHD=∠ODH;
(2)∵四边形ABCD是菱形,
∴OD=OB=BD=3,OA=OC=4,BD⊥AC,
在 Rt△OCD中,CD==5,
∴菱形ABCD的周长=4CD=20,
菱形ABCD的面积=×6×8=24.
13.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴AF∥EC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形;
(2)∵四边形AECF是菱形,
∴AE=EC,
∴∠1=∠2,
∵∠BAC=90°,
∴∠3=90°﹣∠2,∠4=90°﹣∠1,
∴∠3=∠4,
∴AE=BE,
∴BE=AE=CE=BC=4.
14.解:∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°,
∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,
∵DE=CE,
∴四边形DFCE是正方形.
15.证明:如图,∵ABCD为正方形,
∴DC=CB,∠DCB=90°,∠DCF=∠BCF=45°,
在△DFC与△BFC中,
,
∴△DFC≌△BFC(SAS),
∴∠1=∠6,
∵BH为中线,
∴BH=GH,
∴∠3=∠4,
∵∠4=∠5,∠5+∠6=90°,
∴∠1+∠3=90°,
即BF⊥CH.
16.(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)∵四边形ABEF是正方形,
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∵AD=AE,
∴AD﹣AF=AE﹣AG,
即DF=EG,
在△DFO和△EGO中,,
∴△DFO≌△EGO(AAS),
∴FO=GO,FD=EG
∵∠DAE=∠AEF=45°,∠AFE=∠AGD=90°,
∴DF=FO=OG=EG,
∴DO=OF=OG,
∴DG=DO+OG=OG+OG=1,
∴OG==﹣1,
∴OD=(﹣1)=2﹣.
