6.4多边形的内角和与外角和 基础训练-2020-2021学年北师大版八年级数学下册(Word版 含答案)
文档属性
| 名称 | 6.4多边形的内角和与外角和 基础训练-2020-2021学年北师大版八年级数学下册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 55.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 10:31:45 | ||
图片预览

文档简介
平行四边形
第4节《多边形的内角和与内角和》同步基础训练
选择。
1.六边形的内角和为(
)
A.360°
B.540°
C.720°
D.180°
2.一个多边形的每一个内角都是
,这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.八边形
3.一个多边形截去一个角(不过顶点)后,形成的多边形的内角和是2520°,那么原多边形的边数是(
)
A.13
B.14
C.15
D.13或15
4.一个多边形的每个内角均为120°,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
5.四边形中,如果有一组对角都是直角,那么另一组对角一定( )
A.都是钝角
B.都是锐角
C.是一个锐角、一个钝角
D.互补
6.一个正多边形的每个外角都是36°,那么它是(
)
A.正六边形
B.正八边形
C.正十边形
D.正十二边形
7.某校初一数学兴趣小组对教材《多边形的内角和与外角和》的内容进行热烈的讨论,甲说:“多边形的边数每增加1,则内角和增加180°”;乙说:“多边形的边数每增加1,则外角和增加180°”;丙说:“多边形的内角和不小于其外角和”;丁说:“只要是多边形,外角和都是360°”.你认为正确的是( )
A.甲和丁
B.乙和丙
C.丙和丁
D.以上都不对
8.如图所示,小明从点出发,沿直线前进8米后左转,再沿直线前进8米,又左转,照这样走下去,他第一次回到出发点时,一共走了(
)米.
A.70
B.72
C.74
D.76
9.一个多边形的每一个外角都等于40°,那么这个多边形的内角和为( )
A.1260°
B.900°
C.1620°
D.360°
10.一个多边形的边数由原来的3增加到n时(n>3,且n为正整数),它的外角和( )
A.增加(n﹣2)×180°
B.减小(n﹣2)×180°
C.增加(n﹣1)×180°
D.没有改变
二、填空。
11.一个多边形的内角和是它的外角和的4倍,则这个多边形的边数是________.
12.若正n边形的内角和等于它的外角和,则边数n为_____.
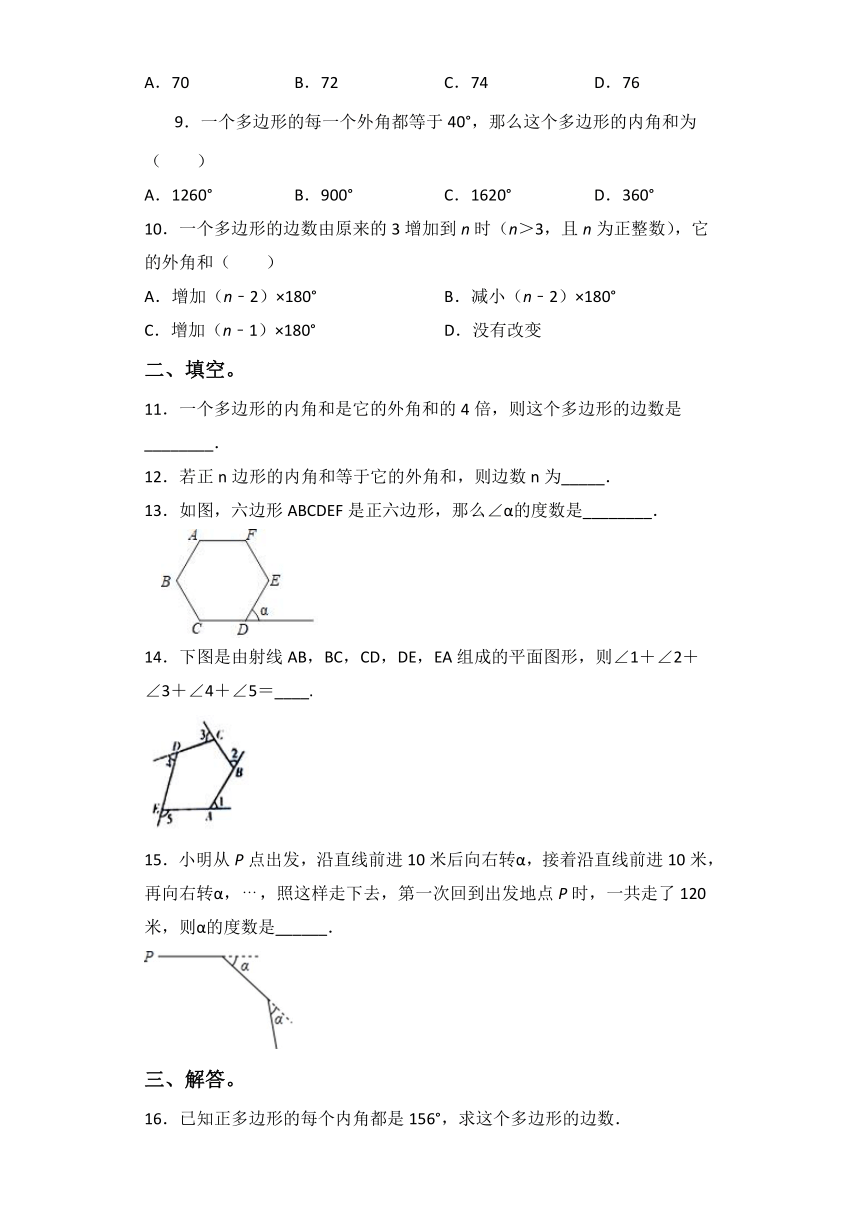
13.如图,六边形ABCDEF是正六边形,那么∠α的度数是________.
14.下图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=____.
15.小明从P点出发,沿直线前进10米后向右转α,接着沿直线前进10米,再向右转α,,照这样走下去,第一次回到出发地点P时,一共走了120米,则α的度数是______.
三、解答。
16.已知正多边形的每个内角都是156°,求这个多边形的边数.
17.已知:如图,五边形ABCDE中,AB∥CD,求图形中∠AED的值.
18.已知一个多边形的每个内角都比相邻外角的3倍还多20°,求这个多边形的内角和.
19.已知一个多边形的每个内角都相等,且一个内角比一个外角大36°,求这个多边形的边数。
20.已知某多边形的内角和与外角和的比是7∶2,求这个多边形的边数.
试卷第1页,总3页
答案
1-5:CBCCD
6-10:CABAD
11.十
12.4
13.60°
14.360°
15.30°
16.15
【详解】
解:设这个多边形的边数为n,
由题意得(n-2)×180=156×n,
解得n=15,
即这个多边形的边数为15.
17.50°.
【详解】
∵AB∥CD,
∴∠B=180°﹣∠C=120°,
∵五边形ABCDE内角和为(5﹣2)×180°=540°,
∴在五边形ABCDE中,∠AED=540°﹣150°﹣120°﹣60°﹣160°=50°.
18.1260°
【解析】
设多边形内角的相邻角为α,则内角等于3α+20°
∴(3α+20°)+α=180°
α=40°
∵每个内角都比相邻的外角的3倍还多20°,即多边形的每个外角为40°
又∵多边形的外角和为360°
∴多边形的外角个数==9
∴多边形的边数=9
多边形的内角和=(9-2)·180°=1260°
19.5
【解析】
解:设内角是x°,外角是y°,到一个
方程组
解得:
由任何多边形的外角是360°,则多边形中外角的个数是360÷72=5,
所以这个多边形的边数是5.
20.这个多边形的边数为9.
【详解】
设这个多边形的边数为n,
则有,
解得:n=9.
∴这个多边形的边数为9.
第4节《多边形的内角和与内角和》同步基础训练
选择。
1.六边形的内角和为(
)
A.360°
B.540°
C.720°
D.180°
2.一个多边形的每一个内角都是
,这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.八边形
3.一个多边形截去一个角(不过顶点)后,形成的多边形的内角和是2520°,那么原多边形的边数是(
)
A.13
B.14
C.15
D.13或15
4.一个多边形的每个内角均为120°,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
5.四边形中,如果有一组对角都是直角,那么另一组对角一定( )
A.都是钝角
B.都是锐角
C.是一个锐角、一个钝角
D.互补
6.一个正多边形的每个外角都是36°,那么它是(
)
A.正六边形
B.正八边形
C.正十边形
D.正十二边形
7.某校初一数学兴趣小组对教材《多边形的内角和与外角和》的内容进行热烈的讨论,甲说:“多边形的边数每增加1,则内角和增加180°”;乙说:“多边形的边数每增加1,则外角和增加180°”;丙说:“多边形的内角和不小于其外角和”;丁说:“只要是多边形,外角和都是360°”.你认为正确的是( )
A.甲和丁
B.乙和丙
C.丙和丁
D.以上都不对
8.如图所示,小明从点出发,沿直线前进8米后左转,再沿直线前进8米,又左转,照这样走下去,他第一次回到出发点时,一共走了(
)米.
A.70
B.72
C.74
D.76
9.一个多边形的每一个外角都等于40°,那么这个多边形的内角和为( )
A.1260°
B.900°
C.1620°
D.360°
10.一个多边形的边数由原来的3增加到n时(n>3,且n为正整数),它的外角和( )
A.增加(n﹣2)×180°
B.减小(n﹣2)×180°
C.增加(n﹣1)×180°
D.没有改变
二、填空。
11.一个多边形的内角和是它的外角和的4倍,则这个多边形的边数是________.
12.若正n边形的内角和等于它的外角和,则边数n为_____.
13.如图,六边形ABCDEF是正六边形,那么∠α的度数是________.
14.下图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=____.
15.小明从P点出发,沿直线前进10米后向右转α,接着沿直线前进10米,再向右转α,,照这样走下去,第一次回到出发地点P时,一共走了120米,则α的度数是______.
三、解答。
16.已知正多边形的每个内角都是156°,求这个多边形的边数.
17.已知:如图,五边形ABCDE中,AB∥CD,求图形中∠AED的值.
18.已知一个多边形的每个内角都比相邻外角的3倍还多20°,求这个多边形的内角和.
19.已知一个多边形的每个内角都相等,且一个内角比一个外角大36°,求这个多边形的边数。
20.已知某多边形的内角和与外角和的比是7∶2,求这个多边形的边数.
试卷第1页,总3页
答案
1-5:CBCCD
6-10:CABAD
11.十
12.4
13.60°
14.360°
15.30°
16.15
【详解】
解:设这个多边形的边数为n,
由题意得(n-2)×180=156×n,
解得n=15,
即这个多边形的边数为15.
17.50°.
【详解】
∵AB∥CD,
∴∠B=180°﹣∠C=120°,
∵五边形ABCDE内角和为(5﹣2)×180°=540°,
∴在五边形ABCDE中,∠AED=540°﹣150°﹣120°﹣60°﹣160°=50°.
18.1260°
【解析】
设多边形内角的相邻角为α,则内角等于3α+20°
∴(3α+20°)+α=180°
α=40°
∵每个内角都比相邻的外角的3倍还多20°,即多边形的每个外角为40°
又∵多边形的外角和为360°
∴多边形的外角个数==9
∴多边形的边数=9
多边形的内角和=(9-2)·180°=1260°
19.5
【解析】
解:设内角是x°,外角是y°,到一个
方程组
解得:
由任何多边形的外角是360°,则多边形中外角的个数是360÷72=5,
所以这个多边形的边数是5.
20.这个多边形的边数为9.
【详解】
设这个多边形的边数为n,
则有,
解得:n=9.
∴这个多边形的边数为9.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
