6.3三角形的中位线 基础训练-2020-2021学年北师大版八年级数学下册(Word版 含答案)
文档属性
| 名称 | 6.3三角形的中位线 基础训练-2020-2021学年北师大版八年级数学下册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 291.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 10:33:18 | ||
图片预览



文档简介
平行四边形
第3节《三角形的中位线》同步基础训练
选择。
1.如图,是等边三角形,D,E,F为各边中点,则图中的等边三角形有(
)
A.2个
B.3个
C.4个
D.5个
2.如图,在中,分别是的平分线,于点于点,的周长为30,,则的长是(
)
A.15
B.9
C.6
D.3
3.如图,点、分别是边、的中点,,则的长为( )
A.
B.
C.
D.
4.如图,在?ABCD中,AD=8,点E,F分别是AB,AC的中点,则EF等于( )
A.2
B.3
C.4
D.5
5.如图,△ABC中,D,E,F,G分别是AB,AC,AD,AE的中点,若BC=8,则DE+FG等于(
)
A.4.5
B.6
C.7
D.8
6.下列叙述不正确的是(
)
A.一个三角形必有三条中位线
B.一个三角形必有三条中线
C.三角形的一条中线分成的两个三角形的面积相等
D.三角形的一条中位线分成的两部分面积相等
7.如图,在△ABC中,点M,N分别是AB,AC的中点,延长CB至点D,使MN=BD,连接DN,若CD=6,则MN的长为( )
A.2
B.3
C.4
D.6
8.如图是屋架设计图的一部分,D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=4
m,∠A=30°,则DE等于
(
)
A.1m
B.2m
C.3m
D.4m
9.三角形的三条中位线长分别为3cm,4cm,6cm,则原三角形的周长为(
)
A.6.
5cm
B.34cm
C
26cm
D.52cm
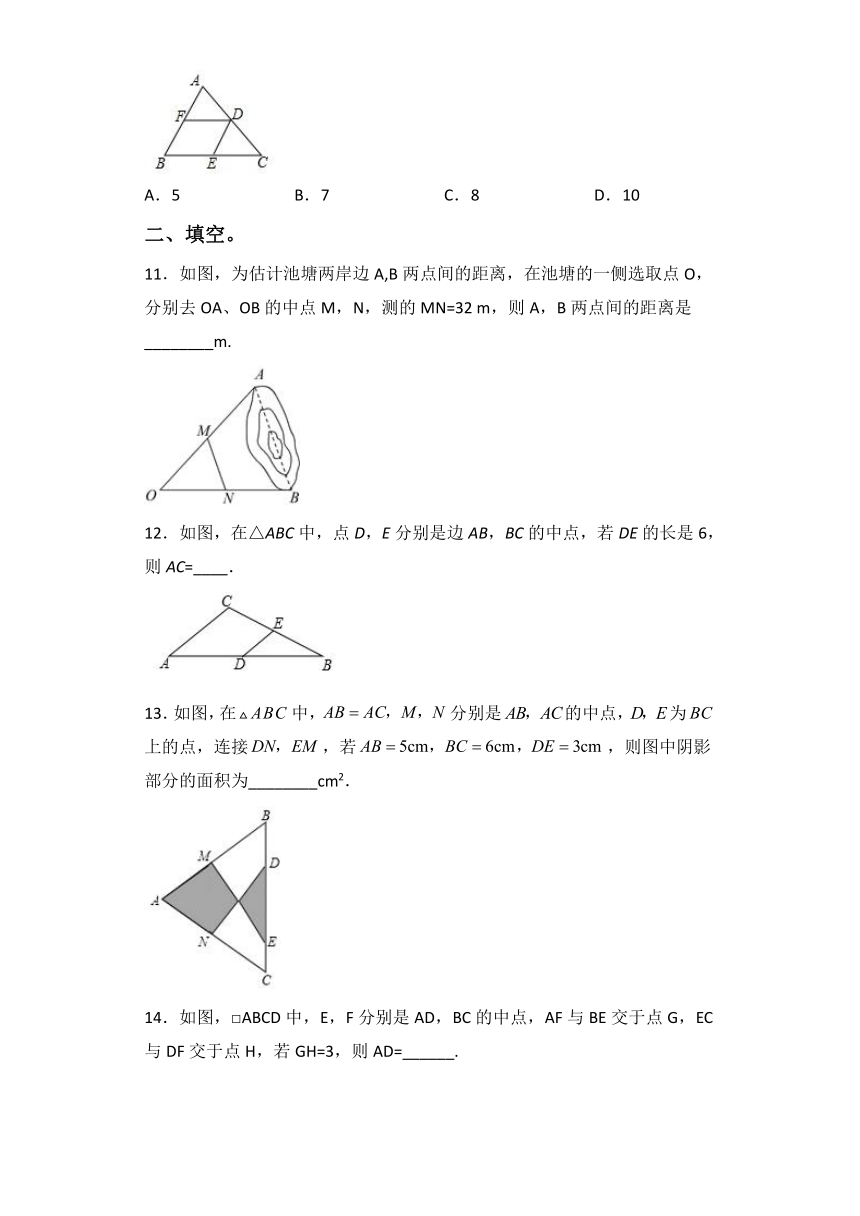
10.如图,在△ABC中,AB=4,BC=6,DE、DF是△ABC的中位线,则四边形BEDF的周长是(
)
A.5
B.7
C.8
D.10
填空。
11.如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别去OA、OB的中点M,N,测的MN=32
m,则A,B两点间的距离是________m.
12.如图,在△ABC中,点D,E分别是边AB,BC的中点,若DE的长是6,则AC=____.
13.如图,在中,分别是的中点,为上的点,连接,若,则图中阴影部分的面积为________cm2.
14.如图,□ABCD中,E,F分别是AD,BC的中点,AF与BE交于点G,EC与DF交于点H,若GH=3,则AD=______.
15.如图,在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AC于点E.∠A=30°,AB=8,则DE的长度是_____.
解答。
16.如图所示,为中边的延长线上一点,且,连接,分别交、于点、,连接交于点,连接,判断与的位置关系和大小关系,并证明你的结论.
17.(1)如图1,在四边形ABCD中,F、E分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE,求证:AB=CD;(提示取BD的中点H,连结FH,HE作辅助线)
(2)如图2,在△ABC中,且O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA的延长线于点G,若AB=DC=5,∠OEC=60°,求OE的长度.
18.已知:如图,在△ABC中,DE、DF是△ABC的中位线,连接EF、AD,其交点为O.求证:
(1)△CDE≌△DBF;
(2)OA=OD.
19.如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.
20.如图,已知:四边形ABCD中,AD=BC,E、F分别是DC、AB的中点,直线EF分别与BC、AD的延长线相交于G、H.
求证:∠AHF=∠BGF.
试卷第1页,总3页
答案
1-5:DDDCB
6-10:DAACD
11.64.
12.12.
13.6
14.6
15.2
16.位置关系:,数量关系:,理由见解析.
【详解】
位置关系:,数量关系:.
理由:∵四边形是平行四边形,
∴,,,
∴,.
∵,
∴,
∴.
∴.
∵,
∴是的中位线,
∴,.
17.(1)证明见解析;(2)OE=.
【解析】
(1)
证明:如图一,连结BD,取DB的中点H,连结EH、FH.
∵E、F分别是AD、BC的中点,
∴EH∥AB,EH=AB,FH∥CD,FH=CD,
∵∠BME=∠CNE,
∴∠HEF=∠HFE,
∴HE=HF,
∴AB=CD;
(2)
如图二,连结BD,取DB的中点H,连结EH、OH,
∵AB=CD,HE为△ABD的中位线,HO为△BCD的中位线,
∴HO=HE=AB=CD,,
∴∠HOE=∠HEO,
∵OH∥AC,∠OEC=60°,
∴∠OEH=∠HOE=∠OEC=60°,
∴△OEH是等边三角形,
∵AB=DC=5,
∴OE=.
18.证明见解析
【解析】
证明:(1)∵DE、DF是△ABC的中位线,∴DF=CE,DF∥CE,DB=DC.∵DF∥CE,∴∠C=∠BDF.
在△CDE和△DBF中,∴△CDE≌△DBF
(SAS);
(2)∵DE、DF是△ABC的中位线,∴DF=AE,DF∥AE,∴四边形DEAF是平行四边形,
∵EF与AD交于O点,∴AO=OD
19.证明见解析.
【解析】
证明:如图,连接BD,作BD的中点M,连接EM、FM,如图所示:
∵点E是AD的中点,
∴在△ABD中,EM∥AB,EM=AB,
∴∠MEF=∠P,
同理可证:FM∥CD,FM=CD.
∴∠MGH=∠DFH.
又∵AB=CD,
∴EM=FM,
∴∠MEF=∠MFE,
∴∠P=∠CQF.
20.证明见解析.
【解析】
证明:连接AC,作EM∥AD交AC于M,连接MF.如下图:
∵E是CD的中点,且EM∥AD,∴EM=AD,M是AC的中点.又∵F是AB的中点,∴MF∥BC,且MF=BC.
∵AD=BC,∴EM=MF,∴∠MEF=∠MFE.
∵EM∥AH,∴∠MEF=∠AHF.∵FM∥BG,∴∠MFE=∠BGF,∴∠AHF=∠BGF.
第3节《三角形的中位线》同步基础训练
选择。
1.如图,是等边三角形,D,E,F为各边中点,则图中的等边三角形有(
)
A.2个
B.3个
C.4个
D.5个
2.如图,在中,分别是的平分线,于点于点,的周长为30,,则的长是(
)
A.15
B.9
C.6
D.3
3.如图,点、分别是边、的中点,,则的长为( )
A.
B.
C.
D.
4.如图,在?ABCD中,AD=8,点E,F分别是AB,AC的中点,则EF等于( )
A.2
B.3
C.4
D.5
5.如图,△ABC中,D,E,F,G分别是AB,AC,AD,AE的中点,若BC=8,则DE+FG等于(
)
A.4.5
B.6
C.7
D.8
6.下列叙述不正确的是(
)
A.一个三角形必有三条中位线
B.一个三角形必有三条中线
C.三角形的一条中线分成的两个三角形的面积相等
D.三角形的一条中位线分成的两部分面积相等
7.如图,在△ABC中,点M,N分别是AB,AC的中点,延长CB至点D,使MN=BD,连接DN,若CD=6,则MN的长为( )
A.2
B.3
C.4
D.6
8.如图是屋架设计图的一部分,D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=4
m,∠A=30°,则DE等于
(
)
A.1m
B.2m
C.3m
D.4m
9.三角形的三条中位线长分别为3cm,4cm,6cm,则原三角形的周长为(
)
A.6.
5cm
B.34cm
C
26cm
D.52cm
10.如图,在△ABC中,AB=4,BC=6,DE、DF是△ABC的中位线,则四边形BEDF的周长是(
)
A.5
B.7
C.8
D.10
填空。
11.如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别去OA、OB的中点M,N,测的MN=32
m,则A,B两点间的距离是________m.
12.如图,在△ABC中,点D,E分别是边AB,BC的中点,若DE的长是6,则AC=____.
13.如图,在中,分别是的中点,为上的点,连接,若,则图中阴影部分的面积为________cm2.
14.如图,□ABCD中,E,F分别是AD,BC的中点,AF与BE交于点G,EC与DF交于点H,若GH=3,则AD=______.
15.如图,在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AC于点E.∠A=30°,AB=8,则DE的长度是_____.
解答。
16.如图所示,为中边的延长线上一点,且,连接,分别交、于点、,连接交于点,连接,判断与的位置关系和大小关系,并证明你的结论.
17.(1)如图1,在四边形ABCD中,F、E分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE,求证:AB=CD;(提示取BD的中点H,连结FH,HE作辅助线)
(2)如图2,在△ABC中,且O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA的延长线于点G,若AB=DC=5,∠OEC=60°,求OE的长度.
18.已知:如图,在△ABC中,DE、DF是△ABC的中位线,连接EF、AD,其交点为O.求证:
(1)△CDE≌△DBF;
(2)OA=OD.
19.如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.
20.如图,已知:四边形ABCD中,AD=BC,E、F分别是DC、AB的中点,直线EF分别与BC、AD的延长线相交于G、H.
求证:∠AHF=∠BGF.
试卷第1页,总3页
答案
1-5:DDDCB
6-10:DAACD
11.64.
12.12.
13.6
14.6
15.2
16.位置关系:,数量关系:,理由见解析.
【详解】
位置关系:,数量关系:.
理由:∵四边形是平行四边形,
∴,,,
∴,.
∵,
∴,
∴.
∴.
∵,
∴是的中位线,
∴,.
17.(1)证明见解析;(2)OE=.
【解析】
(1)
证明:如图一,连结BD,取DB的中点H,连结EH、FH.
∵E、F分别是AD、BC的中点,
∴EH∥AB,EH=AB,FH∥CD,FH=CD,
∵∠BME=∠CNE,
∴∠HEF=∠HFE,
∴HE=HF,
∴AB=CD;
(2)
如图二,连结BD,取DB的中点H,连结EH、OH,
∵AB=CD,HE为△ABD的中位线,HO为△BCD的中位线,
∴HO=HE=AB=CD,,
∴∠HOE=∠HEO,
∵OH∥AC,∠OEC=60°,
∴∠OEH=∠HOE=∠OEC=60°,
∴△OEH是等边三角形,
∵AB=DC=5,
∴OE=.
18.证明见解析
【解析】
证明:(1)∵DE、DF是△ABC的中位线,∴DF=CE,DF∥CE,DB=DC.∵DF∥CE,∴∠C=∠BDF.
在△CDE和△DBF中,∴△CDE≌△DBF
(SAS);
(2)∵DE、DF是△ABC的中位线,∴DF=AE,DF∥AE,∴四边形DEAF是平行四边形,
∵EF与AD交于O点,∴AO=OD
19.证明见解析.
【解析】
证明:如图,连接BD,作BD的中点M,连接EM、FM,如图所示:
∵点E是AD的中点,
∴在△ABD中,EM∥AB,EM=AB,
∴∠MEF=∠P,
同理可证:FM∥CD,FM=CD.
∴∠MGH=∠DFH.
又∵AB=CD,
∴EM=FM,
∴∠MEF=∠MFE,
∴∠P=∠CQF.
20.证明见解析.
【解析】
证明:连接AC,作EM∥AD交AC于M,连接MF.如下图:
∵E是CD的中点,且EM∥AD,∴EM=AD,M是AC的中点.又∵F是AB的中点,∴MF∥BC,且MF=BC.
∵AD=BC,∴EM=MF,∴∠MEF=∠MFE.
∵EM∥AH,∴∠MEF=∠AHF.∵FM∥BG,∴∠MFE=∠BGF,∴∠AHF=∠BGF.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
