18.1.2 平行四边形的判定课件(27张)
文档属性
| 名称 | 18.1.2 平行四边形的判定课件(27张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 907.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 00:00:00 | ||
图片预览



文档简介
18.1.2
平行四边形判定
第十八章
平行四边形
第1课时
平行四边形的判定(1)
情境引入
学习目标
1.运用类比的方法,探索平行四边形的判定方法;
2.理解平行四边形的判定方法,并会简单运用;
3.平行四边形的性质和判定的综合运用.
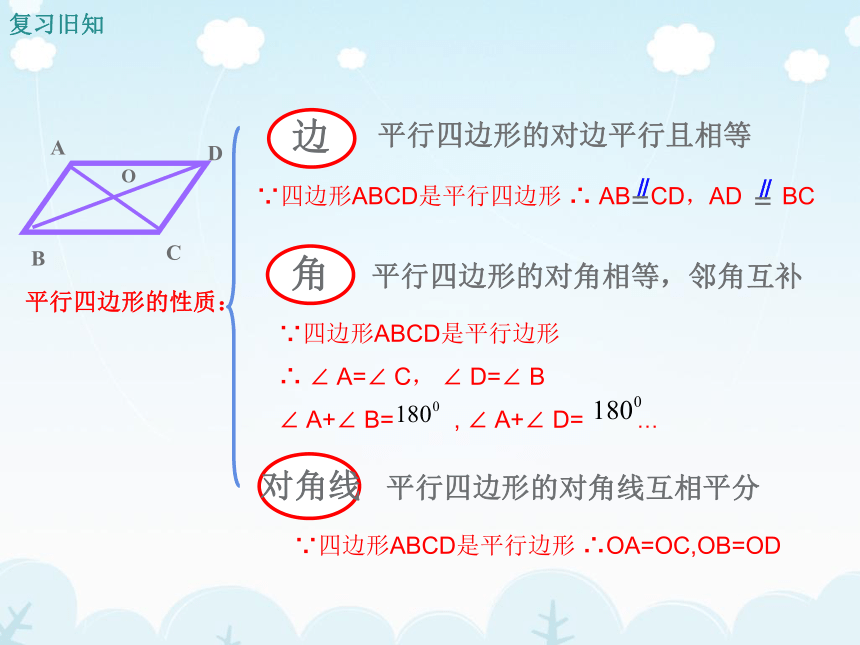
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形
∴
AB
CD,AD
BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴
∠
A=∠
C,
∠
D=∠
B
∠
A+∠
B=
,
∠
A+∠
D=
…
∵四边形ABCD是平行边形
∴OA=OC,OB=OD
复习旧知
通过前面的学习,我们知道,平行四边形的对边相等、对角相等、对角线互相平分,那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
你能根据平行四边形的定义证明它们吗?
活动:探究平行四边形的判定
导入新课
导入新课
学行四边形之后,小明回家用细木棒钉制了一个平行四边形.第二天,小明拿着自己动手做的平行四边形向同学们展示.
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……
讲授新课
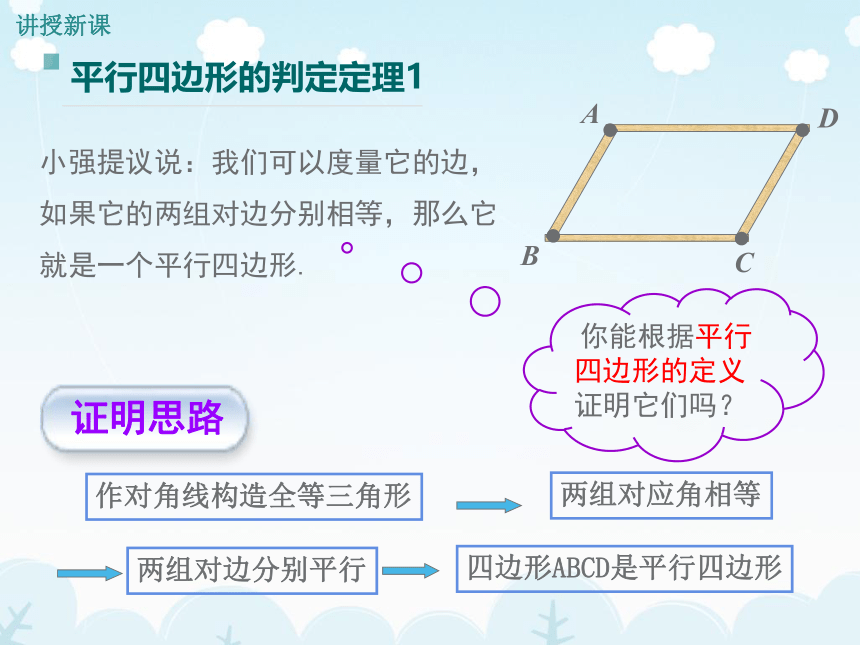
平行四边形的判定定理1
小强提议说:我们可以度量它的边,如果它的两组对边分别相等,那么它就是一个平行四边形.
A
B
C
D
你能根据平行四边形的定义证明它们吗?
证明思路
作对角线构造全等三角形
两组对应角相等
两组对边分别平行
四边形ABCD是平行四边形
∴
∠1=∠4
,
∠
2=∠3
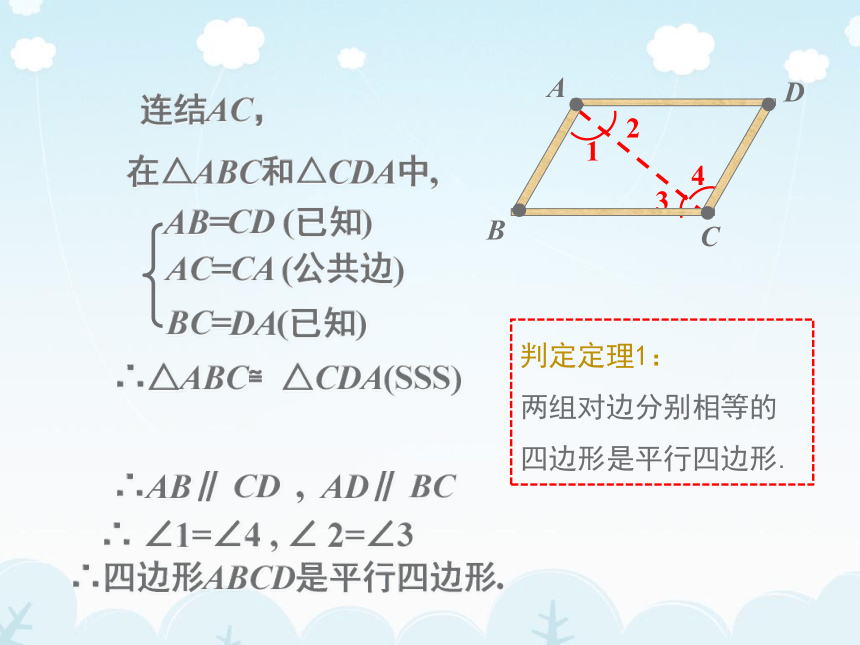
连结AC,
在△ABC和△CDA中,
AB=CD
(已知)
BC=DA(已知)
AC=CA
(公共边)
∴△ABC≌△CDA(SSS)
∴AB∥
CD
,
AD∥
BC
∴四边形ABCD是平行四边形.
1
4
2
3
A
B
C
D
判定定理1:
两组对边分别相等的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形
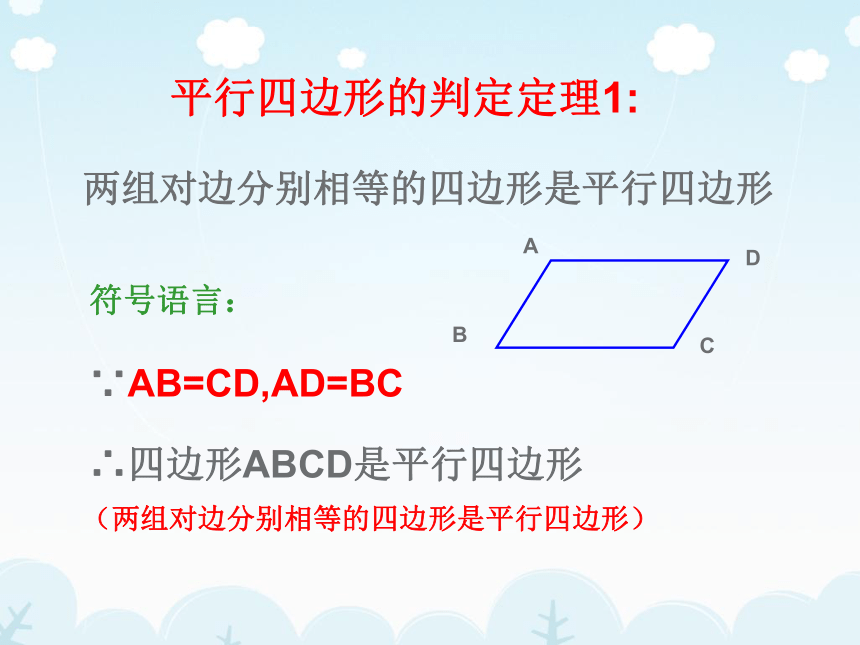
平行四边形的判定定理1:
符号语言:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
A
B
C
D
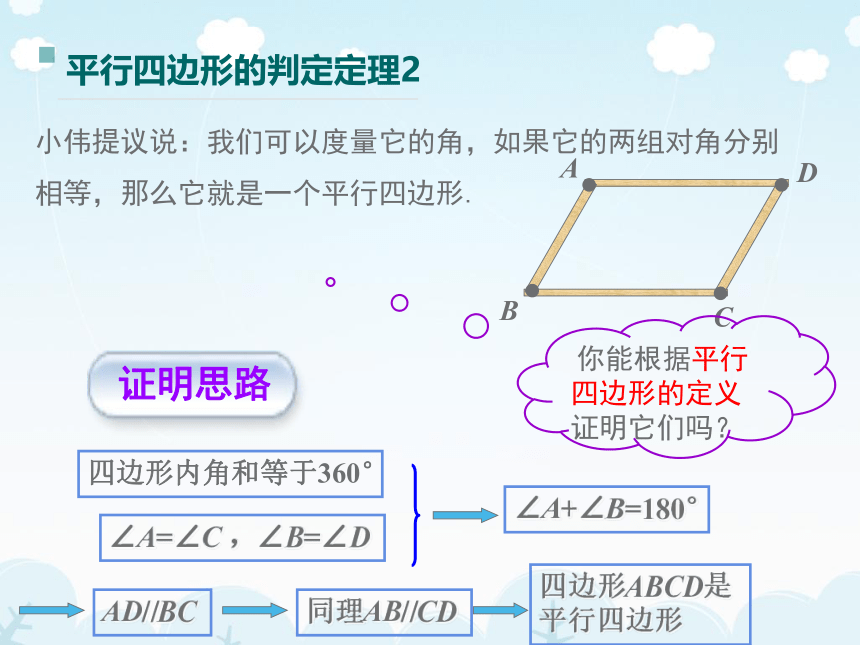
小伟提议说:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形.
A
B
C
D
你能根据平行四边形的定义证明它们吗?
平行四边形的判定定理2
四边形内角和等于360°
∠A=∠C
,∠B=∠D
∠A+∠B=180°
AD//BC
同理AB//CD
四边形ABCD是平行四边形
证明思路
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:
判定定理2:
两组对角分别相等的四边形是平行四边形
∵∠A+∠C+∠B+∠D=3600
又∵∠A=∠C,∠B=∠D
∴2∠A+2∠B=3600
即∠A+∠B=1800
∴
AD∥
BC
∴四边形ABCD是平行四边形.
同理得
AB∥
CD
两组对角分别相等的四边形是平行四边形
平行四边形的判定定理3:
符号语言:
A
B
C
D
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形)
平行四边形的判定定理3
小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形.”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号.然后分别把两条对角线沿记号点对折,发现它们被记号的点分成的两段都能重合,小丽高兴地说:
“这的确是个平行四边形!”
你能用平行四边形的定义进行证明吗?
对顶角相等.
A
B
C
D
O
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边
形ABCD是平行四边形.
判定定理3:
对角线互相平分的四边形是平行四边形
证明:
在△AOB和△COD中,
OA=OC
(已知)
OB=OD
(已知)
∠AOB=∠COD
(对顶角相等)
∴△AOB≌△COD(SAS)
∴
∠BAO=∠OCD
,
∠
ABO=∠CDO
∴AB∥
CD
,
AD∥
BC
∴四边形ABCD是平行四边形.
D
O
A
B
C
对角线互相平分的四边形是平行四边形
平行四边形的判定定理3:
符号语言:
A
B
C
D
O
∵
OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
归纳小结
判定
定理1
定理2
定理3
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,
∴四边形ABCD是
ABCD
A
B
C
D
∵
∠
A=
∠
C,
∠
B=
∠
D,
∴四边形ABCD是
ABCD
A
B
C
D
O
∵AO=CO,BO=DO,
∴四边形ABCD是
ABCD
A
B
C
D
O
AB∥DC
AD∥BC
几何语言描述判定:
AB=DC
AD=BC
ABCD
∠ABC=∠ADC
∠BAD=∠BCD
OA=OC
OB=OD
ABCD
ABCD
ABCD
归纳小结
判断
下列四边形是否为平行四边形?并说出你的依据.
典例精析
例1
例2
填空:如图在四边形ABCD中
(1)若AB//CD,补充条件
,使四边形ABCD为
平行四边形;
(2)若AB=CD,补充条件
,使四边形ABCD为
平行四边形;
(3)若对角线AC、BD交于点O,OA=OC=3,OB=5,
补充条件
,使四边形ABCD为平行四边形.
解题方法:紧扣平行四边形的判定方法补上缺失条件.
AD//BC
AD=BC
OD=5
B
O
D
A
C
典例精析
填空
如图,在□ABCD中,对角线AC,BD相交于点O,
E,F是对角线AC上的两点.请补充一个关于点E,F的条件,使四边形DEBF是平行四边形.你补充的条件是
.
例3
想想还有
其他证法吗?
典例精析
4.如图,在平行四边形ABCD中,已知AE、CF分别是
的角平分线,试说明四边形AFCE是平行四边形.
、
典例精析
想一想:判定一个四边形是平行边形可以从哪些角度思考?具体有哪些方法?
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
从角考虑
两组对角分别相等的四边形是平行四边形(判定定理2)
从对角线考虑
对角线互相平分的四边形是平行四边形(判定定理3)
当堂练习
1.
根据下列条件,不能判定一个四边形为平行四边形的是(
)
A.
两组对边分别相等
B
.
两条对角线互相平分
C
.
两条对角线相等
D
.
两组对边分别平行
分析
C
D
A
B
C
2.
下列命题中,
正确的是(
)
A
两组角相等的四边形是平行四边形
B.
一条对角线平分另
一条对角线的四边形的平行四边形
C一组对边相等,
两条对角线相等的四边形是平行四边形
D两组对边分别相等的四边形是平行四边形、
3.能确定平行四边形的大小和形状的条件是(
)
A.
已知平行四边形的两邻边
B已知平行四边形相邻两角
C已知平行四边形的两对角线
D已知平行四边形的一边、
一条对角
4.能判定四边形ABCD是平行四边形的条件:∠A:∠B:∠C:∠D的值为( )
A.
1:2:3:4
B.
1:4:2:3
C.
1:2:2:1
D.
3:2:3:2
D
5.
如图所示,△ABC是等边三角形,P是其内任意一点,PD//AB,PE//BC,PF//AC,若△ABC的周长为24,则PD+PE+PF=
.
A
F
B
D
C
E
P
8
6.如图,平行四边形ABCD的对角线AC、BD相交于点O,F是OC的中点,E是AO的中点。求证:四边形BFDE是平行四边形.
1.一组对边分别平行的四边形是平行四边形(定义)
两条对角线互相平分的四边形是平行四边形
从边来判定
2.两组对边分别相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
平行四边形的判定方法
课堂小结
47页练习1-4题
课后作业
平行四边形判定
第十八章
平行四边形
第1课时
平行四边形的判定(1)
情境引入
学习目标
1.运用类比的方法,探索平行四边形的判定方法;
2.理解平行四边形的判定方法,并会简单运用;
3.平行四边形的性质和判定的综合运用.
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形
∴
AB
CD,AD
BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴
∠
A=∠
C,
∠
D=∠
B
∠
A+∠
B=
,
∠
A+∠
D=
…
∵四边形ABCD是平行边形
∴OA=OC,OB=OD
复习旧知
通过前面的学习,我们知道,平行四边形的对边相等、对角相等、对角线互相平分,那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
你能根据平行四边形的定义证明它们吗?
活动:探究平行四边形的判定
导入新课
导入新课
学行四边形之后,小明回家用细木棒钉制了一个平行四边形.第二天,小明拿着自己动手做的平行四边形向同学们展示.
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……
讲授新课
平行四边形的判定定理1
小强提议说:我们可以度量它的边,如果它的两组对边分别相等,那么它就是一个平行四边形.
A
B
C
D
你能根据平行四边形的定义证明它们吗?
证明思路
作对角线构造全等三角形
两组对应角相等
两组对边分别平行
四边形ABCD是平行四边形
∴
∠1=∠4
,
∠
2=∠3
连结AC,
在△ABC和△CDA中,
AB=CD
(已知)
BC=DA(已知)
AC=CA
(公共边)
∴△ABC≌△CDA(SSS)
∴AB∥
CD
,
AD∥
BC
∴四边形ABCD是平行四边形.
1
4
2
3
A
B
C
D
判定定理1:
两组对边分别相等的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形
平行四边形的判定定理1:
符号语言:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
A
B
C
D
小伟提议说:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形.
A
B
C
D
你能根据平行四边形的定义证明它们吗?
平行四边形的判定定理2
四边形内角和等于360°
∠A=∠C
,∠B=∠D
∠A+∠B=180°
AD//BC
同理AB//CD
四边形ABCD是平行四边形
证明思路
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:
判定定理2:
两组对角分别相等的四边形是平行四边形
∵∠A+∠C+∠B+∠D=3600
又∵∠A=∠C,∠B=∠D
∴2∠A+2∠B=3600
即∠A+∠B=1800
∴
AD∥
BC
∴四边形ABCD是平行四边形.
同理得
AB∥
CD
两组对角分别相等的四边形是平行四边形
平行四边形的判定定理3:
符号语言:
A
B
C
D
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形)
平行四边形的判定定理3
小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形.”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号.然后分别把两条对角线沿记号点对折,发现它们被记号的点分成的两段都能重合,小丽高兴地说:
“这的确是个平行四边形!”
你能用平行四边形的定义进行证明吗?
对顶角相等.
A
B
C
D
O
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边
形ABCD是平行四边形.
判定定理3:
对角线互相平分的四边形是平行四边形
证明:
在△AOB和△COD中,
OA=OC
(已知)
OB=OD
(已知)
∠AOB=∠COD
(对顶角相等)
∴△AOB≌△COD(SAS)
∴
∠BAO=∠OCD
,
∠
ABO=∠CDO
∴AB∥
CD
,
AD∥
BC
∴四边形ABCD是平行四边形.
D
O
A
B
C
对角线互相平分的四边形是平行四边形
平行四边形的判定定理3:
符号语言:
A
B
C
D
O
∵
OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
归纳小结
判定
定理1
定理2
定理3
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,
∴四边形ABCD是
ABCD
A
B
C
D
∵
∠
A=
∠
C,
∠
B=
∠
D,
∴四边形ABCD是
ABCD
A
B
C
D
O
∵AO=CO,BO=DO,
∴四边形ABCD是
ABCD
A
B
C
D
O
AB∥DC
AD∥BC
几何语言描述判定:
AB=DC
AD=BC
ABCD
∠ABC=∠ADC
∠BAD=∠BCD
OA=OC
OB=OD
ABCD
ABCD
ABCD
归纳小结
判断
下列四边形是否为平行四边形?并说出你的依据.
典例精析
例1
例2
填空:如图在四边形ABCD中
(1)若AB//CD,补充条件
,使四边形ABCD为
平行四边形;
(2)若AB=CD,补充条件
,使四边形ABCD为
平行四边形;
(3)若对角线AC、BD交于点O,OA=OC=3,OB=5,
补充条件
,使四边形ABCD为平行四边形.
解题方法:紧扣平行四边形的判定方法补上缺失条件.
AD//BC
AD=BC
OD=5
B
O
D
A
C
典例精析
填空
如图,在□ABCD中,对角线AC,BD相交于点O,
E,F是对角线AC上的两点.请补充一个关于点E,F的条件,使四边形DEBF是平行四边形.你补充的条件是
.
例3
想想还有
其他证法吗?
典例精析
4.如图,在平行四边形ABCD中,已知AE、CF分别是
的角平分线,试说明四边形AFCE是平行四边形.
、
典例精析
想一想:判定一个四边形是平行边形可以从哪些角度思考?具体有哪些方法?
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
从角考虑
两组对角分别相等的四边形是平行四边形(判定定理2)
从对角线考虑
对角线互相平分的四边形是平行四边形(判定定理3)
当堂练习
1.
根据下列条件,不能判定一个四边形为平行四边形的是(
)
A.
两组对边分别相等
B
.
两条对角线互相平分
C
.
两条对角线相等
D
.
两组对边分别平行
分析
C
D
A
B
C
2.
下列命题中,
正确的是(
)
A
两组角相等的四边形是平行四边形
B.
一条对角线平分另
一条对角线的四边形的平行四边形
C一组对边相等,
两条对角线相等的四边形是平行四边形
D两组对边分别相等的四边形是平行四边形、
3.能确定平行四边形的大小和形状的条件是(
)
A.
已知平行四边形的两邻边
B已知平行四边形相邻两角
C已知平行四边形的两对角线
D已知平行四边形的一边、
一条对角
4.能判定四边形ABCD是平行四边形的条件:∠A:∠B:∠C:∠D的值为( )
A.
1:2:3:4
B.
1:4:2:3
C.
1:2:2:1
D.
3:2:3:2
D
5.
如图所示,△ABC是等边三角形,P是其内任意一点,PD//AB,PE//BC,PF//AC,若△ABC的周长为24,则PD+PE+PF=
.
A
F
B
D
C
E
P
8
6.如图,平行四边形ABCD的对角线AC、BD相交于点O,F是OC的中点,E是AO的中点。求证:四边形BFDE是平行四边形.
1.一组对边分别平行的四边形是平行四边形(定义)
两条对角线互相平分的四边形是平行四边形
从边来判定
2.两组对边分别相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
平行四边形的判定方法
课堂小结
47页练习1-4题
课后作业
