2020-2021学年人教版七年级数学下册平行线中的拐点(拐角)问题专题(共18张PPT)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册平行线中的拐点(拐角)问题专题(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 823.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 15:18:32 | ||
图片预览




文档简介
(共18张PPT)
专题:平行线中的拐点问题
第五章
相交线与平行线
复习巩固
掌握平行线中“拐角”问题作辅助线的方法以及处理该类问题的方法技能.
1、平行线的性质与判定?
2、平行线的传递性。
复习巩固
新课探究
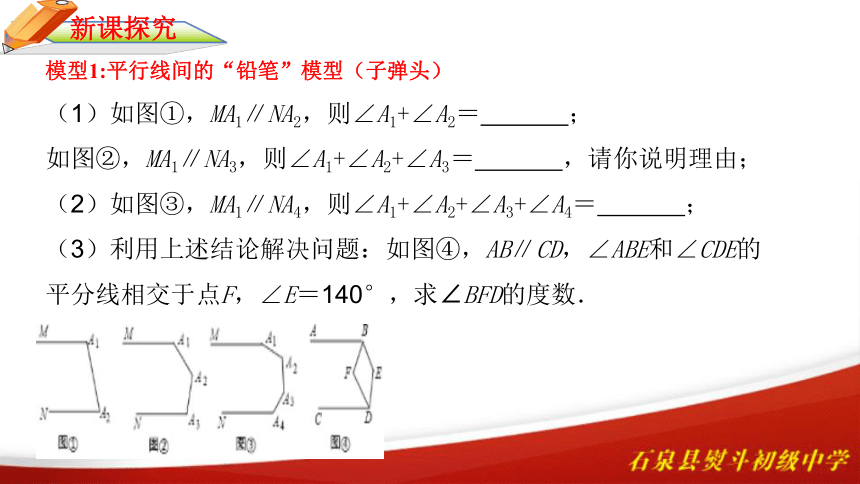
模型1:平行线间的“铅笔”模型(子弹头)
(1)如图①,MA1∥NA2,则∠A1+∠A2=
;
如图②,MA1∥NA3,则∠A1+∠A2+∠A3=
,请你说明理由;
(2)如图③,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=
;
(3)利用上述结论解决问题:如图④,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠E=140°,求∠BFD的度数.
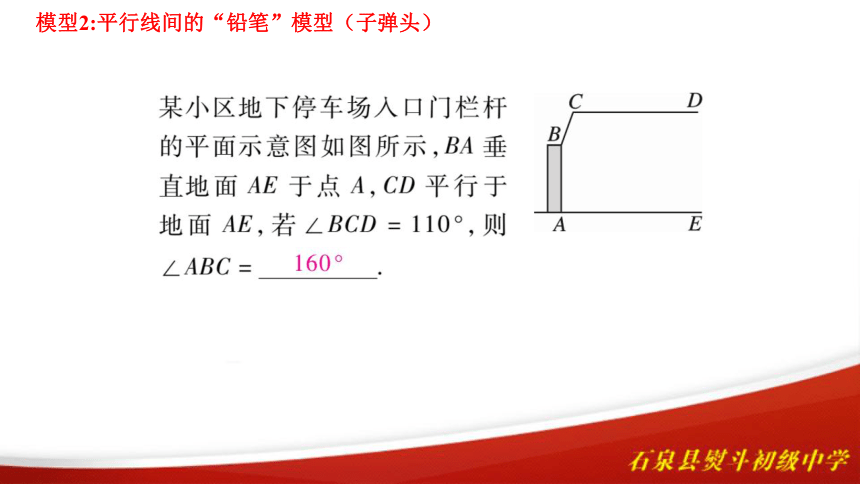
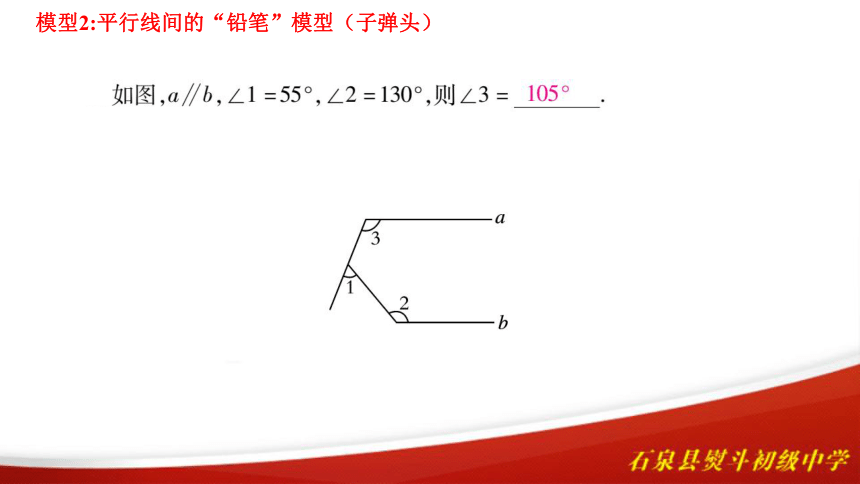
模型2:平行线间的“铅笔”模型(子弹头)
模型2:平行线间的“铅笔”模型(子弹头)
模型2:平行线间的“M”模型(猪手)
如图α示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC、∠A、∠C的关系,并说明理由.
新课探究
模型2:平行线间的“M”模型(猪手)
如图,AB∥CD,∠A=30。,∠AEC=70.
,则
∠C
=
(2)如图,AB∥EF,BC⊥CD于C,∠ABC=30°,∠DEF=45°,则∠CDE等于( )
A.105°
B.75°
C.135°
D.115°
模型2:平行线间的“M”模型(猪手)
模型3:平行线间的“枝丫”模型(锄头型和犀牛角型)
①已知:AB∥CD,结论:∠AEC=∠A-∠C
②已知:AB∥CD,结论:∠AEC=∠C-∠A
证明:
过点E作EF,使得EF∥AB
∵AB∥CD
∴EF∥CD
∴∠A=∠AEF,∠C=∠CEF
∵∠AEC=∠AEF-∠CEF
∴∠AEC=∠A-∠C
证明:
过点E作EF,使得EF∥AB
∵AB∥CD
∴EF∥CD
∴∠A=∠AEF,∠C=∠CEF
∵∠AEC=∠CEF-∠AEF
∴∠AEC=∠C-∠A
模型3:平行线间的“枝丫”模型(锄头型和犀牛角型)
模型3:平行线间的“枝丫”模型(锄头型和犀牛角型)
小
结
问题1:关于平行线中“拐角”问题,如何添加辅助线?
问题2:如何寻找动角之间的数量关系?
课后检测
1.如图,已知AB∥DE,∠B=20°,∠D=130°,那么∠BCD等于( )
A.60°
B.70°
C.80°
D.90°
2.如图AB∥CD,∠1=140°,∠2=90°,则∠3的度数是( )
A.40°
B.45°
C.50°
D.60°
3.如图所示,若AB∥CD,则∠A,∠D,∠E之间的度数关系是( )
A.∠A+∠E+∠D=180°
B.∠A﹣∠E+∠D=180°
C.∠A+∠E﹣∠D=180°
D.∠A+∠E+∠D=270°
4.如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )
A.72°
B.68°
C.63°
D.18°
课后检测
课后检测
5.如图,直线a∥b,∠1=50°,2=30°,则∠3的度数为( )
A.20°
B.30°
C.40°
D.50°
6.学习平行线的性质后,老师给小明出了一道题:如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是多少度?请你帮小明求出( )
A.120°
B.130°
C.140°
D.150°
课后检测
7.如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为( )
A.30°
B.35°
C.40°
D.45°
A.38°
B.48°
C.42°
D.100°
8.如图,直线a∥b,则∠ABD的度数是( )
课后检测
9.如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
A.10°
B.15°
C.20°
D.25°
10.如图,桌面上有木条b、c固定,木条a在桌面上绕点O旋转n°(0<n<90)后与b平行,则n=( )
A.20
B.30
C.70
D.80
专题:平行线中的拐点问题
第五章
相交线与平行线
复习巩固
掌握平行线中“拐角”问题作辅助线的方法以及处理该类问题的方法技能.
1、平行线的性质与判定?
2、平行线的传递性。
复习巩固
新课探究
模型1:平行线间的“铅笔”模型(子弹头)
(1)如图①,MA1∥NA2,则∠A1+∠A2=
;
如图②,MA1∥NA3,则∠A1+∠A2+∠A3=
,请你说明理由;
(2)如图③,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=
;
(3)利用上述结论解决问题:如图④,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠E=140°,求∠BFD的度数.
模型2:平行线间的“铅笔”模型(子弹头)
模型2:平行线间的“铅笔”模型(子弹头)
模型2:平行线间的“M”模型(猪手)
如图α示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC、∠A、∠C的关系,并说明理由.
新课探究
模型2:平行线间的“M”模型(猪手)
如图,AB∥CD,∠A=30。,∠AEC=70.
,则
∠C
=
(2)如图,AB∥EF,BC⊥CD于C,∠ABC=30°,∠DEF=45°,则∠CDE等于( )
A.105°
B.75°
C.135°
D.115°
模型2:平行线间的“M”模型(猪手)
模型3:平行线间的“枝丫”模型(锄头型和犀牛角型)
①已知:AB∥CD,结论:∠AEC=∠A-∠C
②已知:AB∥CD,结论:∠AEC=∠C-∠A
证明:
过点E作EF,使得EF∥AB
∵AB∥CD
∴EF∥CD
∴∠A=∠AEF,∠C=∠CEF
∵∠AEC=∠AEF-∠CEF
∴∠AEC=∠A-∠C
证明:
过点E作EF,使得EF∥AB
∵AB∥CD
∴EF∥CD
∴∠A=∠AEF,∠C=∠CEF
∵∠AEC=∠CEF-∠AEF
∴∠AEC=∠C-∠A
模型3:平行线间的“枝丫”模型(锄头型和犀牛角型)
模型3:平行线间的“枝丫”模型(锄头型和犀牛角型)
小
结
问题1:关于平行线中“拐角”问题,如何添加辅助线?
问题2:如何寻找动角之间的数量关系?
课后检测
1.如图,已知AB∥DE,∠B=20°,∠D=130°,那么∠BCD等于( )
A.60°
B.70°
C.80°
D.90°
2.如图AB∥CD,∠1=140°,∠2=90°,则∠3的度数是( )
A.40°
B.45°
C.50°
D.60°
3.如图所示,若AB∥CD,则∠A,∠D,∠E之间的度数关系是( )
A.∠A+∠E+∠D=180°
B.∠A﹣∠E+∠D=180°
C.∠A+∠E﹣∠D=180°
D.∠A+∠E+∠D=270°
4.如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )
A.72°
B.68°
C.63°
D.18°
课后检测
课后检测
5.如图,直线a∥b,∠1=50°,2=30°,则∠3的度数为( )
A.20°
B.30°
C.40°
D.50°
6.学习平行线的性质后,老师给小明出了一道题:如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是多少度?请你帮小明求出( )
A.120°
B.130°
C.140°
D.150°
课后检测
7.如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为( )
A.30°
B.35°
C.40°
D.45°
A.38°
B.48°
C.42°
D.100°
8.如图,直线a∥b,则∠ABD的度数是( )
课后检测
9.如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
A.10°
B.15°
C.20°
D.25°
10.如图,桌面上有木条b、c固定,木条a在桌面上绕点O旋转n°(0<n<90)后与b平行,则n=( )
A.20
B.30
C.70
D.80
