六年级下册数学课件 2.5 正比例和反比例 北京版 (23张PPT)
文档属性
| 名称 | 六年级下册数学课件 2.5 正比例和反比例 北京版 (23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 534.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 14:02:01 | ||
图片预览






文档简介
(共23张PPT)
成反比例的量
桃溪镇中心小学
刘胜许
自学提示
①认真观察例2的情境图,你从图中获得了哪些信息?
②表中有哪两种量?这两种量是怎样变化的?两种量相对应的两个数的积各是多少?这个积表示什么意思?
③根据你的学习试着总结一下反比例的意义,用字母式怎样来表示?
④怎样判断两种量是否成反比例?
(结合自学提示,先自主学习,然后在小组内讨论交流)
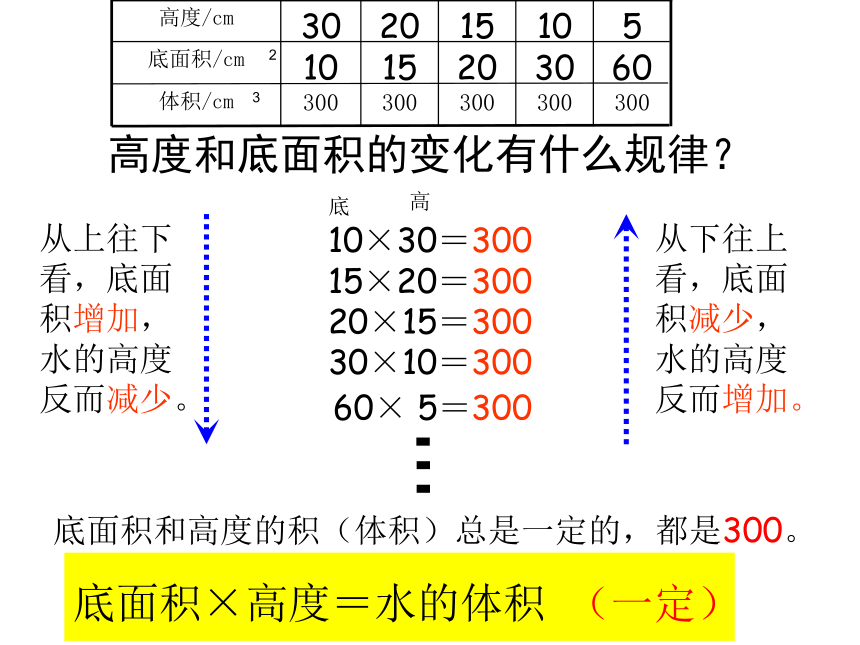
10
30
15
20
30
60
20
15
10
5
仔细观察
认真思考
返回
底面积和高度的积(体积)总是一定的,都是300。
10×30=300
15×20=300
20×15=300
30×10=300
60×
5=300
从上往下看,底面积增加,水的高度反而减少。
从下往上看,底面积减少,水的高度反而增加。
(一定)
底面积×高度=水的体积
高度和底面积的变化有什么规律?
300
300
300
300
300
体积/cm
60
30
20
15
10
底面积/cm
5
10
15
20
30
高度/cm
3
2
底
高
小结:
因为水的高度和杯子的底面积是两种相关联的量,水的高度是随着杯子的底面积变大而不断变小,而且水的高度与杯子的底面积的乘积总是一定的。所以水的高度和杯子的底面积是成反比例的量,水的高度和杯子的底面积成反比例关系。
(1)两种量必须是两种相关联的量
(2)一种量变化,另一种量也随着变化
(3)两种量中相对应的两个数的积一定
反比例的判断标准:
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
x×y=k(一定)
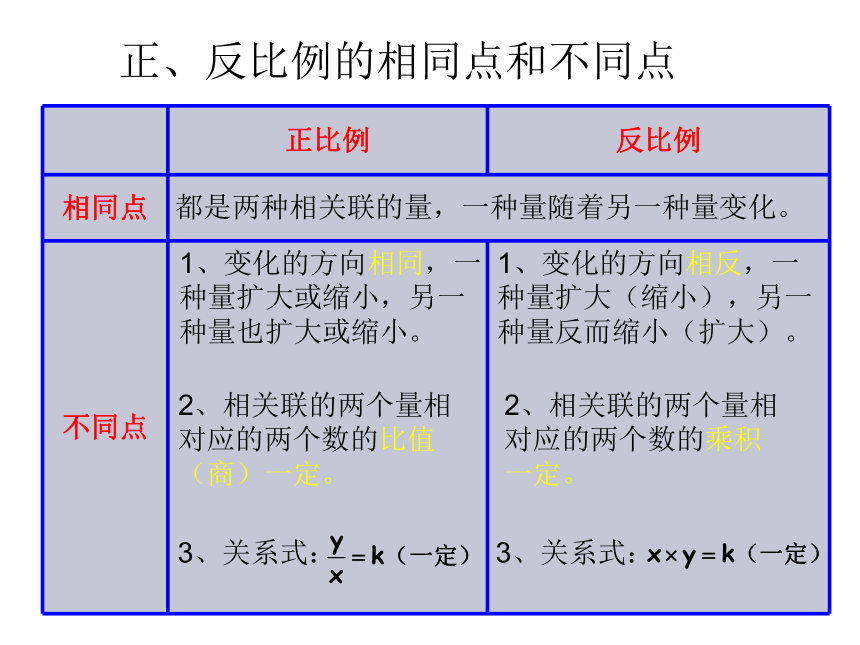
正、反比例的相同点和不同点
正比例
反比例
相同点
不同点
1、变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
都是两种相关联的量,一种量随着另一种量变化。
1、变化的方向相反,一种量扩大(缩小),另一种量反而缩小(扩大)。
2、相关联的两个量相对应的两个数的比值(商)一定。
2、相关联的两个量相对应的两个数的乘积一定。
3、关系式:
3、关系式:
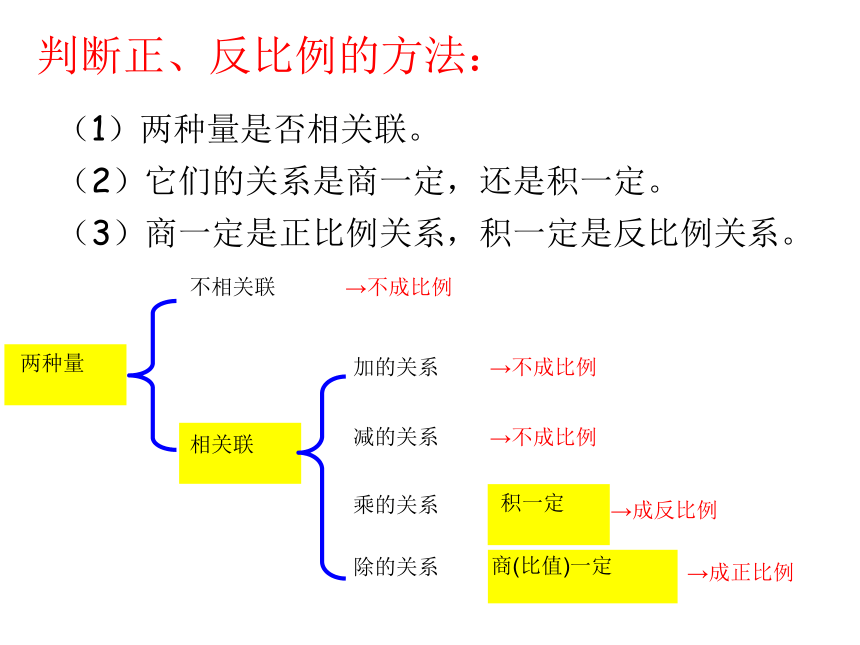
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
商(比值)一定
→成反比例
→成正比例
判断正、反比例的方法:
(1)两种量是否相关联。
(2)它们的关系是商一定,还是积一定。
(3)商一定是正比例关系,积一定是反比例关系。
做一做
运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和需要的天数两种量。
(2)写出几组这两种量中相对应的两个数的积,并比
较积的大小。
300
×1
=300
150
×
2=300
100
×
3=300
每天运的吨数
需
要
的
天
数
300
6
1
150
2
150
100
75
60
50
3
4
5
它们是相关联的量。
75
×4
=300
60
×
5=300
50
×
6=300
(积相等)
做一做
运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(3)说明这个积所表示的意义。
这个积表示的意义是这批货物的总吨数。
(4)表中相关联的两种量成反比例吗?为什么?
每天运的吨数
需
要
的
天
数
300
6
1
150
2
150
100
75
60
50
3
4
5
每天运的吨数和需要的天数是两种相关联的量。
因为:
所以:
每天运的吨数×需要的天数=货物总吨数(一定)
每天运的吨数和需要的天数成反比例。
因为
所以
判断下面每题中的两种量是不是成反比例,并
说明理由。
(1)全班的人数一定,每组人数和组数。
每组人数和组数是两种相关联的量,
每组人数×组数=全班人数(一定)
每组人数和组数成反比例。
因为
所以
判断下面每题中的两种量是不是成反比例,并
说明理由。
(2)圆柱的体积一定,圆柱的底面积和高。
圆柱的底面积和高是两种相关联的量,
圆柱的底面积×高=圆柱的体积(一定)
圆柱的底面积和高反比例。
因为
所以
判断下面每题中的两种量是不是成反比例,并
说明理由。
(3)书的总册数一定,每包的册数和包数。
每包的册数和包数是两种相关联的量,
每包的册数×包数=书的总册数(一定)
每包的册数和包数反比例。
因为
所以
判断下面每题中的两种量是不是成反比例,并
说明理由。
(4)在一块菜地上种的黄瓜和西红柿的面积。
黄瓜和西红柿的面积是两种相关联的量,
黄瓜的面积+西红柿的面积=菜地总面积(一定)
是和一定,不是积一定,
黄瓜和西红柿的面积不成反比例。
1、从图中可以看到这些点在不在同一条直线上?
2、把这些点连起来是一条什么线?
3、反比例图像与正比例图像有什么区别?
4、从图像中你能看出杯子的底面积分别40㎝2、50㎝2、55㎝2时,水的高度分别是多少吗?
观察课本第48页下面的图象,思考下面的问题:
课堂检测:
1、先填表然后再回答问题
用600张纸装订同样的练习本
(1)把表填完整
(2)表中相关联的两种量是(
)和(
),装订本数扩大,每本的页数(
),装订本数缩小,每本的页数(
)。
(3)表中相对应的两个数乘积是(
),这个积表示(
)。
(4)由于(
)×(
)=(
)一定,所以(
)和(
)成(
)关系。
每本页数
15
25
40
60
……
装订本数
30
20
12
……
2、想一想、填一填:
(1)在“工作效率×工作时间=工作总量”关系式中
当工作效率一定时(
)和(
)成(
)比例
当工作总量一定时(
)和(
)和(
)比例
当工作时间一定时(
)和(
)和(
)比例
(2)三角形的(
)一定,(
)和(
)成反比例关系,
(3)在计算圆柱的体积公式中(
)一定,(
)和(
)成反比例关系。
(4)用瓷砖铺教室地面,(
)一定,(
)和(
)成反比例关系。
3、下面的两种量成反比例关系吗?(成反比例打“√”,不成反比例的要说明理由。)
(1)五一班同学排队做操,每行人数与行数。(
)
(2)一本故事书,已看的页数与未看的页数。(
)
(3)正方体的体积一定时,底面积和高。(
)
(4)20÷x=y中,x和y(
)
4、下面各题中,x、y是两种相关联的量,它们是否成比例?成什么比例?请连一连。
x=
y
不成比例
=
成正比例
x×y2=100
成反比例
1
6
2
y
x
3
5、看图填空
420
360
300
240
180
120
60
0
1
2
3
4
5
6
7
路程/千米
时间/时
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
长/cm
宽/
cm
图(1)
图(2)
图(1)是一幅(
)比例图像,从图中我们知道(
)随着(
)的变化而变化,(
)一定的,因此(
)和(
)成(
)关系。
图(2)是一幅(
)比例图像,从图中我们知道(
)随着(
)的变化而变化,(
)一定的,因此(
)和(
)成(
)关系。
课堂总结
通过本节课的学习,你有哪些收获?
再
见!
成反比例的量
桃溪镇中心小学
刘胜许
自学提示
①认真观察例2的情境图,你从图中获得了哪些信息?
②表中有哪两种量?这两种量是怎样变化的?两种量相对应的两个数的积各是多少?这个积表示什么意思?
③根据你的学习试着总结一下反比例的意义,用字母式怎样来表示?
④怎样判断两种量是否成反比例?
(结合自学提示,先自主学习,然后在小组内讨论交流)
10
30
15
20
30
60
20
15
10
5
仔细观察
认真思考
返回
底面积和高度的积(体积)总是一定的,都是300。
10×30=300
15×20=300
20×15=300
30×10=300
60×
5=300
从上往下看,底面积增加,水的高度反而减少。
从下往上看,底面积减少,水的高度反而增加。
(一定)
底面积×高度=水的体积
高度和底面积的变化有什么规律?
300
300
300
300
300
体积/cm
60
30
20
15
10
底面积/cm
5
10
15
20
30
高度/cm
3
2
底
高
小结:
因为水的高度和杯子的底面积是两种相关联的量,水的高度是随着杯子的底面积变大而不断变小,而且水的高度与杯子的底面积的乘积总是一定的。所以水的高度和杯子的底面积是成反比例的量,水的高度和杯子的底面积成反比例关系。
(1)两种量必须是两种相关联的量
(2)一种量变化,另一种量也随着变化
(3)两种量中相对应的两个数的积一定
反比例的判断标准:
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
x×y=k(一定)
正、反比例的相同点和不同点
正比例
反比例
相同点
不同点
1、变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
都是两种相关联的量,一种量随着另一种量变化。
1、变化的方向相反,一种量扩大(缩小),另一种量反而缩小(扩大)。
2、相关联的两个量相对应的两个数的比值(商)一定。
2、相关联的两个量相对应的两个数的乘积一定。
3、关系式:
3、关系式:
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
商(比值)一定
→成反比例
→成正比例
判断正、反比例的方法:
(1)两种量是否相关联。
(2)它们的关系是商一定,还是积一定。
(3)商一定是正比例关系,积一定是反比例关系。
做一做
运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和需要的天数两种量。
(2)写出几组这两种量中相对应的两个数的积,并比
较积的大小。
300
×1
=300
150
×
2=300
100
×
3=300
每天运的吨数
需
要
的
天
数
300
6
1
150
2
150
100
75
60
50
3
4
5
它们是相关联的量。
75
×4
=300
60
×
5=300
50
×
6=300
(积相等)
做一做
运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(3)说明这个积所表示的意义。
这个积表示的意义是这批货物的总吨数。
(4)表中相关联的两种量成反比例吗?为什么?
每天运的吨数
需
要
的
天
数
300
6
1
150
2
150
100
75
60
50
3
4
5
每天运的吨数和需要的天数是两种相关联的量。
因为:
所以:
每天运的吨数×需要的天数=货物总吨数(一定)
每天运的吨数和需要的天数成反比例。
因为
所以
判断下面每题中的两种量是不是成反比例,并
说明理由。
(1)全班的人数一定,每组人数和组数。
每组人数和组数是两种相关联的量,
每组人数×组数=全班人数(一定)
每组人数和组数成反比例。
因为
所以
判断下面每题中的两种量是不是成反比例,并
说明理由。
(2)圆柱的体积一定,圆柱的底面积和高。
圆柱的底面积和高是两种相关联的量,
圆柱的底面积×高=圆柱的体积(一定)
圆柱的底面积和高反比例。
因为
所以
判断下面每题中的两种量是不是成反比例,并
说明理由。
(3)书的总册数一定,每包的册数和包数。
每包的册数和包数是两种相关联的量,
每包的册数×包数=书的总册数(一定)
每包的册数和包数反比例。
因为
所以
判断下面每题中的两种量是不是成反比例,并
说明理由。
(4)在一块菜地上种的黄瓜和西红柿的面积。
黄瓜和西红柿的面积是两种相关联的量,
黄瓜的面积+西红柿的面积=菜地总面积(一定)
是和一定,不是积一定,
黄瓜和西红柿的面积不成反比例。
1、从图中可以看到这些点在不在同一条直线上?
2、把这些点连起来是一条什么线?
3、反比例图像与正比例图像有什么区别?
4、从图像中你能看出杯子的底面积分别40㎝2、50㎝2、55㎝2时,水的高度分别是多少吗?
观察课本第48页下面的图象,思考下面的问题:
课堂检测:
1、先填表然后再回答问题
用600张纸装订同样的练习本
(1)把表填完整
(2)表中相关联的两种量是(
)和(
),装订本数扩大,每本的页数(
),装订本数缩小,每本的页数(
)。
(3)表中相对应的两个数乘积是(
),这个积表示(
)。
(4)由于(
)×(
)=(
)一定,所以(
)和(
)成(
)关系。
每本页数
15
25
40
60
……
装订本数
30
20
12
……
2、想一想、填一填:
(1)在“工作效率×工作时间=工作总量”关系式中
当工作效率一定时(
)和(
)成(
)比例
当工作总量一定时(
)和(
)和(
)比例
当工作时间一定时(
)和(
)和(
)比例
(2)三角形的(
)一定,(
)和(
)成反比例关系,
(3)在计算圆柱的体积公式中(
)一定,(
)和(
)成反比例关系。
(4)用瓷砖铺教室地面,(
)一定,(
)和(
)成反比例关系。
3、下面的两种量成反比例关系吗?(成反比例打“√”,不成反比例的要说明理由。)
(1)五一班同学排队做操,每行人数与行数。(
)
(2)一本故事书,已看的页数与未看的页数。(
)
(3)正方体的体积一定时,底面积和高。(
)
(4)20÷x=y中,x和y(
)
4、下面各题中,x、y是两种相关联的量,它们是否成比例?成什么比例?请连一连。
x=
y
不成比例
=
成正比例
x×y2=100
成反比例
1
6
2
y
x
3
5、看图填空
420
360
300
240
180
120
60
0
1
2
3
4
5
6
7
路程/千米
时间/时
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
长/cm
宽/
cm
图(1)
图(2)
图(1)是一幅(
)比例图像,从图中我们知道(
)随着(
)的变化而变化,(
)一定的,因此(
)和(
)成(
)关系。
图(2)是一幅(
)比例图像,从图中我们知道(
)随着(
)的变化而变化,(
)一定的,因此(
)和(
)成(
)关系。
课堂总结
通过本节课的学习,你有哪些收获?
再
见!
