2020-2021学年人教版七年级下册数学第八章实际问题与二元一次方程组(1)——和差倍分问题课件(26张ppt)
文档属性
| 名称 | 2020-2021学年人教版七年级下册数学第八章实际问题与二元一次方程组(1)——和差倍分问题课件(26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 207.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 06:51:08 | ||
图片预览








文档简介
(共26张PPT)
第一部分
新课内容
第八章
二元一次方程组
第31课时
实际问题与二元一次方程组(1)——
和差倍分问题
目录
01
知识点导学
02
典型例题
03
变式训练
04
分层训练
A.
用二元一次方程组解决实际问题的步骤:
(1)审:理解题意,设________未知数;
(2)找:找出________等量关系;
(3)列:正确列出________;
(4)解:求出________未知数的值;
(5)答:检验后完整写出答案.
知识点导学
两个
两个
方程组
两个
1.
A型号计算器的单价比B型号计算器的单价多12元,5台A型号计算器与7台B型号计算器的价钱相同,求A,B型号计算器的单价.
解:设A,B型号计算器的单价分别为________元,________元.
列方程组,得______________________.
续表
x
y
x=y+12,
5x=7y
典型例题
知识点1:
由实际问题抽象出二元一次方程
【例1】已知甲数的一半与乙数的
的和为100,设甲数为x,乙数为y,列出二元一次方程:____________________________________.
x+
y=100
变式训练
2.
已知甲数的2倍与乙数的
的差为-1,设甲数为x,乙数为y,列出二元一次方程:_______________________________________.
2x-
y=-1
知识点2:
和差问题
【例2】为了抓住2020年六一儿童节的商机,某商场决定购进甲、乙两种玩具进行销售.
若购进甲种玩具1件,乙种玩具2件,需要160元;购进甲种玩具2件,乙种玩具3件,需要280元,则购进甲、乙两种玩具每件各需要多少元?
解:设购进甲种玩具每件需要x元,购进乙种玩具每件需要y元.
根据题意,得
解得
答:购进甲种玩具每件需要80元,购进乙种玩具每件需要40元.
x+2y=160,
2x+3y=280.
x=80,
y=40.
变式训练
3.
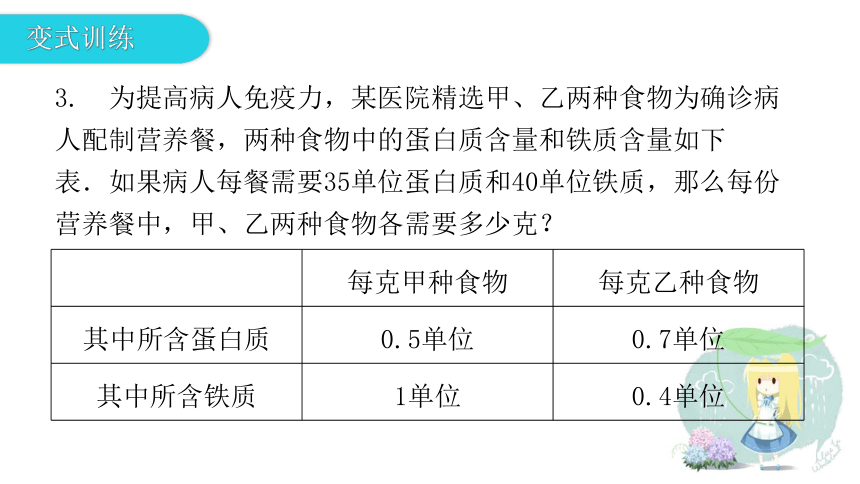
为提高病人免疫力,某医院精选甲、乙两种食物为确诊病人配制营养餐,两种食物中的蛋白质含量和铁质含量如下表.如果病人每餐需要35单位蛋白质和40单位铁质,那么每份营养餐中,甲、乙两种食物各需要多少克?
每克甲种食物
每克乙种食物
其中所含蛋白质
0.5单位
0.7单位
其中所含铁质
1单位
0.4单位
解:设甲、乙两种食物各需要x
g,y
g.
根据题意,得
解得
答:每份营养餐中,甲、乙两种食物各需要28
g,30
g.
0.5x+0.7y=35,
x+0.4y=40.
x=28,
y=30.
知识点3:
倍分问题
【例3】甲、乙两种笔的单价分别为7元,3元,某学校用78元钱买这两种笔作为数学竞赛一、二等奖的奖品,钱恰好用完.若购买乙种笔的数量是甲种笔的两倍,请问两种笔各买了几支?
解:设甲种笔买了x支,乙种笔买了y支.
根据题意,得
解得
答:甲种笔买了6支,乙种笔买了12支.
7x+3y=78,
y=2x.
x=6,
y=12.
变式训练
4.
某企业为严重缺水的甲、乙两所学校捐赠矿泉水共2
000瓶.已知捐给甲校的矿泉水瓶数比捐给乙校的瓶数的2倍少400瓶.求该企业分别向甲、乙两所学校捐了多少瓶矿泉水.
解:设该企业向甲校捐了x瓶矿泉水,向乙校捐了y瓶矿泉水.
由题意,得
解得
答:该企业向甲校捐了1
200瓶矿泉水,向乙校捐了800瓶矿泉水.
x+y=2
000,
x=2y-400.
x=1
200,
y=800.
分层训练
A组
5.
今年植树节这天,我校七年级(3)班有24名同学共种了34棵树苗,其中男生每人种树2棵,女生每人种树1棵.设男生有x人,女生有y人,根据题意,下列方程组正确的是
(
)
A.
B.
C.
D.
x+y=34,
x+2y=24
D
x+y=34,
2x+y=24
x+y=24,
x+2y=34
x+y=24,
2x+y=34
6.
3月份全球疫情加速扩散后,中国已经安排A与B两种型号的包机9架次,从伊朗、意大利等国接回包括留学人员在内的中国公民1
457人.其中A型包机每架次坐满158人,B型包机每架次坐满163人,求A型和B型包机各有多少架?
解:设A型包机有x架,B型包机有y架.
依题意,得
解得
答:A型包机有2架,B型包机有7架.
x+y=9,
158x+163y=1
457.
x=2,
y=7.
B组
7.
用彩色和单色的两种地砖铺地,每块彩色地砖14元,每块单色地砖12元,若单色地砖的数量比彩色地砖的数量的2倍少15块,买两种地砖共用了1
340元,求购买了彩色和单色地砖各多少?
解:设购买彩色地砖x块,单色地砖y块.
依题意,得
解得
答:购买了彩色地砖40块,单色地砖65块.
2x-y=15,
14x+12y=1
340.
x=40,
y=65.
8.
用1块A型钢板可制成4件甲种产品和1件乙种产品;用1块B型钢板可制成3件甲种产品和2件乙种产品.要生产甲种产品45件,乙种产品25件,求恰好需用A,B两种型号的钢板共多少块?
解:设需用A型钢板x块,B型钢板y块.
依题意,得
解得
∴x+y=3+11=14(块).
答:需用A,B两种型号的钢板共14块.
4x+3y=45,
x+2y=25.
x=3,
y=11.
C组
9.
学校有若干个篮球和足球,其中篮球数比足球数的2倍少3个,且篮球数与足球数的比为3∶2,求学校有篮球和足球各多少个.
解:设学校有篮球x个,足球y个.
根据题意,得
解得
答:学校有篮球9个,足球6个.
x=2y-3,
3y=2x.
x=9,
y=6.
10.我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,求井深是多少?
解:设绳长是x尺,井深是y尺.
依题意,得
解得
答:井深是8尺.
x-y=4,
x-y=1.
x=36,
y=8.
谢
谢
第一部分
新课内容
第八章
二元一次方程组
第31课时
实际问题与二元一次方程组(1)——
和差倍分问题
目录
01
知识点导学
02
典型例题
03
变式训练
04
分层训练
A.
用二元一次方程组解决实际问题的步骤:
(1)审:理解题意,设________未知数;
(2)找:找出________等量关系;
(3)列:正确列出________;
(4)解:求出________未知数的值;
(5)答:检验后完整写出答案.
知识点导学
两个
两个
方程组
两个
1.
A型号计算器的单价比B型号计算器的单价多12元,5台A型号计算器与7台B型号计算器的价钱相同,求A,B型号计算器的单价.
解:设A,B型号计算器的单价分别为________元,________元.
列方程组,得______________________.
续表
x
y
x=y+12,
5x=7y
典型例题
知识点1:
由实际问题抽象出二元一次方程
【例1】已知甲数的一半与乙数的
的和为100,设甲数为x,乙数为y,列出二元一次方程:____________________________________.
x+
y=100
变式训练
2.
已知甲数的2倍与乙数的
的差为-1,设甲数为x,乙数为y,列出二元一次方程:_______________________________________.
2x-
y=-1
知识点2:
和差问题
【例2】为了抓住2020年六一儿童节的商机,某商场决定购进甲、乙两种玩具进行销售.
若购进甲种玩具1件,乙种玩具2件,需要160元;购进甲种玩具2件,乙种玩具3件,需要280元,则购进甲、乙两种玩具每件各需要多少元?
解:设购进甲种玩具每件需要x元,购进乙种玩具每件需要y元.
根据题意,得
解得
答:购进甲种玩具每件需要80元,购进乙种玩具每件需要40元.
x+2y=160,
2x+3y=280.
x=80,
y=40.
变式训练
3.
为提高病人免疫力,某医院精选甲、乙两种食物为确诊病人配制营养餐,两种食物中的蛋白质含量和铁质含量如下表.如果病人每餐需要35单位蛋白质和40单位铁质,那么每份营养餐中,甲、乙两种食物各需要多少克?
每克甲种食物
每克乙种食物
其中所含蛋白质
0.5单位
0.7单位
其中所含铁质
1单位
0.4单位
解:设甲、乙两种食物各需要x
g,y
g.
根据题意,得
解得
答:每份营养餐中,甲、乙两种食物各需要28
g,30
g.
0.5x+0.7y=35,
x+0.4y=40.
x=28,
y=30.
知识点3:
倍分问题
【例3】甲、乙两种笔的单价分别为7元,3元,某学校用78元钱买这两种笔作为数学竞赛一、二等奖的奖品,钱恰好用完.若购买乙种笔的数量是甲种笔的两倍,请问两种笔各买了几支?
解:设甲种笔买了x支,乙种笔买了y支.
根据题意,得
解得
答:甲种笔买了6支,乙种笔买了12支.
7x+3y=78,
y=2x.
x=6,
y=12.
变式训练
4.
某企业为严重缺水的甲、乙两所学校捐赠矿泉水共2
000瓶.已知捐给甲校的矿泉水瓶数比捐给乙校的瓶数的2倍少400瓶.求该企业分别向甲、乙两所学校捐了多少瓶矿泉水.
解:设该企业向甲校捐了x瓶矿泉水,向乙校捐了y瓶矿泉水.
由题意,得
解得
答:该企业向甲校捐了1
200瓶矿泉水,向乙校捐了800瓶矿泉水.
x+y=2
000,
x=2y-400.
x=1
200,
y=800.
分层训练
A组
5.
今年植树节这天,我校七年级(3)班有24名同学共种了34棵树苗,其中男生每人种树2棵,女生每人种树1棵.设男生有x人,女生有y人,根据题意,下列方程组正确的是
(
)
A.
B.
C.
D.
x+y=34,
x+2y=24
D
x+y=34,
2x+y=24
x+y=24,
x+2y=34
x+y=24,
2x+y=34
6.
3月份全球疫情加速扩散后,中国已经安排A与B两种型号的包机9架次,从伊朗、意大利等国接回包括留学人员在内的中国公民1
457人.其中A型包机每架次坐满158人,B型包机每架次坐满163人,求A型和B型包机各有多少架?
解:设A型包机有x架,B型包机有y架.
依题意,得
解得
答:A型包机有2架,B型包机有7架.
x+y=9,
158x+163y=1
457.
x=2,
y=7.
B组
7.
用彩色和单色的两种地砖铺地,每块彩色地砖14元,每块单色地砖12元,若单色地砖的数量比彩色地砖的数量的2倍少15块,买两种地砖共用了1
340元,求购买了彩色和单色地砖各多少?
解:设购买彩色地砖x块,单色地砖y块.
依题意,得
解得
答:购买了彩色地砖40块,单色地砖65块.
2x-y=15,
14x+12y=1
340.
x=40,
y=65.
8.
用1块A型钢板可制成4件甲种产品和1件乙种产品;用1块B型钢板可制成3件甲种产品和2件乙种产品.要生产甲种产品45件,乙种产品25件,求恰好需用A,B两种型号的钢板共多少块?
解:设需用A型钢板x块,B型钢板y块.
依题意,得
解得
∴x+y=3+11=14(块).
答:需用A,B两种型号的钢板共14块.
4x+3y=45,
x+2y=25.
x=3,
y=11.
C组
9.
学校有若干个篮球和足球,其中篮球数比足球数的2倍少3个,且篮球数与足球数的比为3∶2,求学校有篮球和足球各多少个.
解:设学校有篮球x个,足球y个.
根据题意,得
解得
答:学校有篮球9个,足球6个.
x=2y-3,
3y=2x.
x=9,
y=6.
10.我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,求井深是多少?
解:设绳长是x尺,井深是y尺.
依题意,得
解得
答:井深是8尺.
x-y=4,
x-y=1.
x=36,
y=8.
谢
谢
