人教版七年级下册7.1.1有序数对课件(22张ppt)
文档属性
| 名称 | 人教版七年级下册7.1.1有序数对课件(22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 284.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 07:01:56 | ||
图片预览






文档简介
有序数对
七年级下册
学习目标
1、会用有序数对表示物体的位置;
2、结合用有序数对表示物体的位置的内容,体会数形结合的思想.
1.有序数对(2,5)和(5,2)表示的含义_________.(填“相同”或“不同”)
2.用3和6组成一个有序数对,可以写成( )
A.(3,6) B.(6,3)
C.3,6或6,3 D.(3,6)或(6,3)
3.下列数据不能用有序数对表示的是( )
A.4楼,5楼 B.6楼,8号
C.3号路,25号 D.东经110°,北纬67°
不同
D
A
预习检测
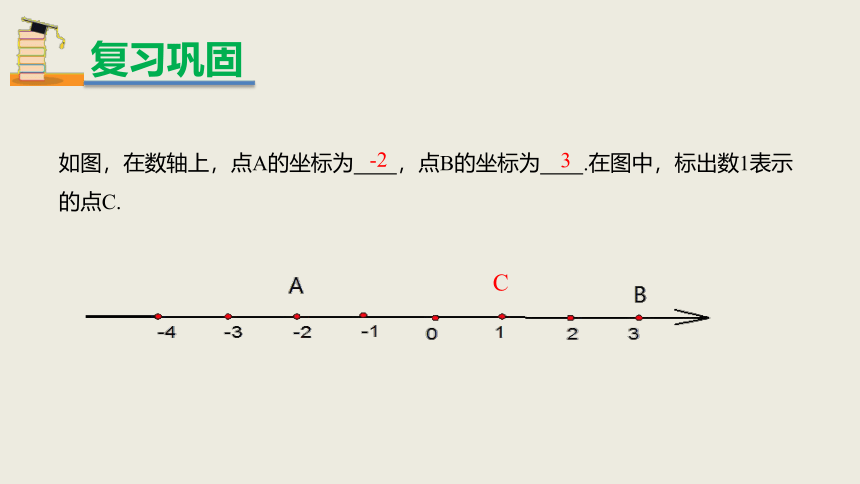
如图,在数轴上,点A的坐标为 ,点B的坐标为 .在图中,标出数1表示的点C.
-2
3
C
复习巩固
近期剧院举办周杰伦个人演唱会,小华与朋友买了两张票去观看,座位号分别是7排9号和7排11号。怎样才能既快又准地找到座位?
先找排数,再找号数
周杰伦演唱会
周杰伦演唱会
课堂导入
问题⑴: 在班里老师想找一个学生回答问题,你知道是谁吗?
问题(2): 你认为确定一个位置需要几个数据?
提示一: 只给一个数据“第2列”,你能确定老师要找的同学是谁吗?
提示二: 给出两个数据“第2列,第3排”,你能确定是谁了吗?
找同学
课堂探究
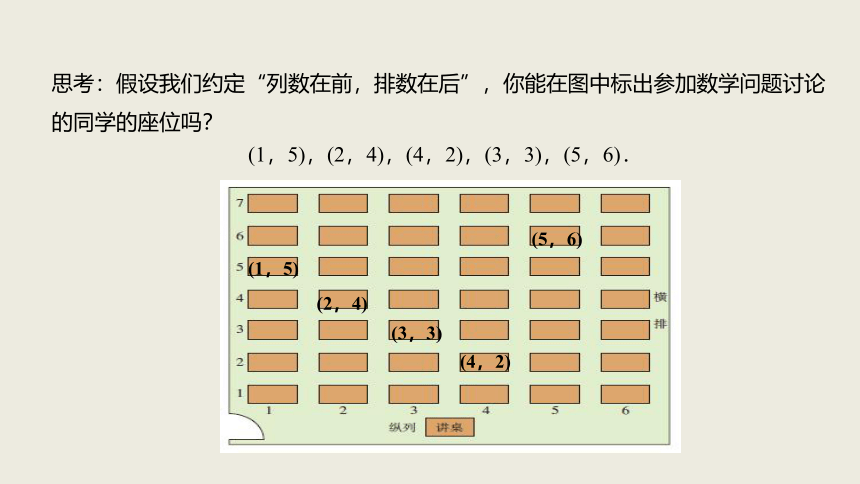
如图是一个教室平面图,你能根据以下座位找到对应的同学参加数学问题讨论吗?
(1,5),(2,4),(4,2),(3,3),(5,6).
课堂活动
思考:假设我们约定“列数在前,排数在后”,你能在图中标出参加数学问题讨论的同学的座位吗?
(1,5)
(2,4)
(4,2)
(3,3)
(5,6)
(1,5),(2,4),(4,2),(3,3),(5,6).
由上面可知,“第1列第3排”简记为(1,3)(约定列在前,排在后),那么“第3列第5排”能简记成什么?(6,7)表示的含义是什么?
“第3列第5排”记为(3,5);(6,7)表示的含义是第6列第7排.
同样约定“列数在前,排数在后”,(2,4)和(4,2)在同一个位置吗?
两者不在同一个位置.因为(2,4)表示第2列第4排,(4,2)表示第4列第2排.
思考
用含有两个数的表达方式来表示一个确定的位置,其中各个数表示不同的含义,我们把这种有顺序的两个数a与b组成的数对,叫做有序数对。
有序:指数a与b是有顺序的,(a, b)与(b, a)是两个不同的数对;
记作: (a,b)
数对:是指必须由两个数才能确定,并且数a与b是有特定含义的;
概念
有序数对表示平面内的点,每个点与有序数对一一对应.
例 1 “贪吃蛇”是一种计算机游戏,图中的●标志表示“蛇”先后经过的几个位置,如果用(1,2)表示“蛇”经过的第2个位置,那么你能用同样的方式表示出图中“蛇”经过的其他几个位置吗?
1
2
3
4
5
1
2
3
4
5
6
7
8
排
列
例题解析
1
2
3
4
5
1
2
3
4
5
6
7
8
(1,2)
(1,1)
(3,2)
(3,3)
(4,3)
(4,5)
(5,5)
(5,4)
(7,4)
(7,3)
(8,3)
排
列
8
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(9,6)
(8,5)
(3,7)
(6,8)
(7,4)
(2,2)
(3,3)
(5,2)
写出学校里各个地点表示的有序数对.
尝试练习
例2:同学们一起去电影院看电影,小明不小心把电影票弄脏了(如图).
(1)他也记不清原来的数字是什么,他能很快找到自己的座位吗?为什么?
(2)通过上面的例子,你认为用几个数字能确定平面内一点的位置?
(3)如果将“8排6座”记作(8,6),那么“7排10座”如何表示?
(4)(3,6)表示什么位置?(6,3)又表示什么位置?它们的位置是否相同?
答案:(1)不能;
(2)两个数字;
(3)(7,10);
(4)3排6座;6排3座;不相同
例题解析
1、根据下列表述,能确定具体位置是( )
A.某电影院2排 B.金寨南路
C.北偏东45° D.东经168°,北纬15°
2、某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )
A.第3组第2排 B.第3组第1排
C.第2组第3排 D、第2组第2排
尝试练习
D
C
1、一个有序数对( )
A.可以确定一个点的位置 B.可以确定两个点的位置
C.可以确定一个或两个点的位置 D.不能确定点的位置
2、在电影院内,如果将“12排8号”记作(12,8),那么“5排9号”怎样表示?(23,15)表示的含义是什么?( )
A.(9,5);23排15号 B.(5,9);23排15号
C.(9,5);15排23号 D.(5,9);15排23号
随堂检测
A
B
3、上课时,李明、刘军、王海三位同学的位置如图所示,若李明的位置是(0,0),刘军的位置是(3,2),那么王海的位置是( )
A.(5,4) B.(4,5) C.(5,5) D.(4,4)
4、如图,如果四角星的顶点A的位置用(5,8)表示,那么顶点B的位置可以表示为________.
A
(2,5)
5、如图是围棋盘的左下角呈现的一局围棋比赛中的几手棋.为方便记录棋谱,横线用数字表示,纵线用英文字母表示,这样,黑棋?的位置可记为(C,4),白棋②的位置可记为(E,3),则白棋⑨的位置应记为____________,(I,4)表示的是____________.
(D,6)
黑棋⑧
6、如图,李老师家在2街与2巷的十字路口附近,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4) 表示李老师从家到学校上班的一条路线.请你用同样的方式写出从家到学校的另外一种路线:
答案不唯一:
如(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4)
a表示: 排、列、纬度、角度……
b表示: 号、排、经度、距离……
①有序数对的概念;
②平面内的点可由一个有序数对来表示,记作(a,b);
③可用有序数对表示实际问题;
④用有序数对可绘成各种图案.
课堂小结
布置作业
书面作业:完成相关书本作业
再见
七年级下册
学习目标
1、会用有序数对表示物体的位置;
2、结合用有序数对表示物体的位置的内容,体会数形结合的思想.
1.有序数对(2,5)和(5,2)表示的含义_________.(填“相同”或“不同”)
2.用3和6组成一个有序数对,可以写成( )
A.(3,6) B.(6,3)
C.3,6或6,3 D.(3,6)或(6,3)
3.下列数据不能用有序数对表示的是( )
A.4楼,5楼 B.6楼,8号
C.3号路,25号 D.东经110°,北纬67°
不同
D
A
预习检测
如图,在数轴上,点A的坐标为 ,点B的坐标为 .在图中,标出数1表示的点C.
-2
3
C
复习巩固
近期剧院举办周杰伦个人演唱会,小华与朋友买了两张票去观看,座位号分别是7排9号和7排11号。怎样才能既快又准地找到座位?
先找排数,再找号数
周杰伦演唱会
周杰伦演唱会
课堂导入
问题⑴: 在班里老师想找一个学生回答问题,你知道是谁吗?
问题(2): 你认为确定一个位置需要几个数据?
提示一: 只给一个数据“第2列”,你能确定老师要找的同学是谁吗?
提示二: 给出两个数据“第2列,第3排”,你能确定是谁了吗?
找同学
课堂探究
如图是一个教室平面图,你能根据以下座位找到对应的同学参加数学问题讨论吗?
(1,5),(2,4),(4,2),(3,3),(5,6).
课堂活动
思考:假设我们约定“列数在前,排数在后”,你能在图中标出参加数学问题讨论的同学的座位吗?
(1,5)
(2,4)
(4,2)
(3,3)
(5,6)
(1,5),(2,4),(4,2),(3,3),(5,6).
由上面可知,“第1列第3排”简记为(1,3)(约定列在前,排在后),那么“第3列第5排”能简记成什么?(6,7)表示的含义是什么?
“第3列第5排”记为(3,5);(6,7)表示的含义是第6列第7排.
同样约定“列数在前,排数在后”,(2,4)和(4,2)在同一个位置吗?
两者不在同一个位置.因为(2,4)表示第2列第4排,(4,2)表示第4列第2排.
思考
用含有两个数的表达方式来表示一个确定的位置,其中各个数表示不同的含义,我们把这种有顺序的两个数a与b组成的数对,叫做有序数对。
有序:指数a与b是有顺序的,(a, b)与(b, a)是两个不同的数对;
记作: (a,b)
数对:是指必须由两个数才能确定,并且数a与b是有特定含义的;
概念
有序数对表示平面内的点,每个点与有序数对一一对应.
例 1 “贪吃蛇”是一种计算机游戏,图中的●标志表示“蛇”先后经过的几个位置,如果用(1,2)表示“蛇”经过的第2个位置,那么你能用同样的方式表示出图中“蛇”经过的其他几个位置吗?
1
2
3
4
5
1
2
3
4
5
6
7
8
排
列
例题解析
1
2
3
4
5
1
2
3
4
5
6
7
8
(1,2)
(1,1)
(3,2)
(3,3)
(4,3)
(4,5)
(5,5)
(5,4)
(7,4)
(7,3)
(8,3)
排
列
8
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(9,6)
(8,5)
(3,7)
(6,8)
(7,4)
(2,2)
(3,3)
(5,2)
写出学校里各个地点表示的有序数对.
尝试练习
例2:同学们一起去电影院看电影,小明不小心把电影票弄脏了(如图).
(1)他也记不清原来的数字是什么,他能很快找到自己的座位吗?为什么?
(2)通过上面的例子,你认为用几个数字能确定平面内一点的位置?
(3)如果将“8排6座”记作(8,6),那么“7排10座”如何表示?
(4)(3,6)表示什么位置?(6,3)又表示什么位置?它们的位置是否相同?
答案:(1)不能;
(2)两个数字;
(3)(7,10);
(4)3排6座;6排3座;不相同
例题解析
1、根据下列表述,能确定具体位置是( )
A.某电影院2排 B.金寨南路
C.北偏东45° D.东经168°,北纬15°
2、某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )
A.第3组第2排 B.第3组第1排
C.第2组第3排 D、第2组第2排
尝试练习
D
C
1、一个有序数对( )
A.可以确定一个点的位置 B.可以确定两个点的位置
C.可以确定一个或两个点的位置 D.不能确定点的位置
2、在电影院内,如果将“12排8号”记作(12,8),那么“5排9号”怎样表示?(23,15)表示的含义是什么?( )
A.(9,5);23排15号 B.(5,9);23排15号
C.(9,5);15排23号 D.(5,9);15排23号
随堂检测
A
B
3、上课时,李明、刘军、王海三位同学的位置如图所示,若李明的位置是(0,0),刘军的位置是(3,2),那么王海的位置是( )
A.(5,4) B.(4,5) C.(5,5) D.(4,4)
4、如图,如果四角星的顶点A的位置用(5,8)表示,那么顶点B的位置可以表示为________.
A
(2,5)
5、如图是围棋盘的左下角呈现的一局围棋比赛中的几手棋.为方便记录棋谱,横线用数字表示,纵线用英文字母表示,这样,黑棋?的位置可记为(C,4),白棋②的位置可记为(E,3),则白棋⑨的位置应记为____________,(I,4)表示的是____________.
(D,6)
黑棋⑧
6、如图,李老师家在2街与2巷的十字路口附近,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4) 表示李老师从家到学校上班的一条路线.请你用同样的方式写出从家到学校的另外一种路线:
答案不唯一:
如(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4)
a表示: 排、列、纬度、角度……
b表示: 号、排、经度、距离……
①有序数对的概念;
②平面内的点可由一个有序数对来表示,记作(a,b);
③可用有序数对表示实际问题;
④用有序数对可绘成各种图案.
课堂小结
布置作业
书面作业:完成相关书本作业
再见
