17.2 勾股定理的逆定理同步练习题(含答案)
文档属性
| 名称 | 17.2 勾股定理的逆定理同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 15:04:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级数学勾股定理逆定理章节测试卷
姓名:
分数:
一、单选题(每题3分;共36分)
1.下列结论中,正确的有(??
)
①△ABC的三边长分别为a,b,c,若b2+c2=a2
,
则△ABC是直角三角形;②在Rt△ABC中,已知两边长分别为6和8,则第三边的长为10;③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;④若三角形的三边长之比为1:2:
,则该三角形是直角三角形.
A.?3个???????????????????????????????????????B.?2个???????????????????????????????????????C.?1个???????????????????????????????????????D.?0个
2.等腰三角形一腰长为5,这一腰上的高为3,则这个等腰三角形底边长为(??
)
A.?????????????????????????????B.?????????????????????????????C.?
或
????????????????????????????D.?4或
3.在平面直角坐标系中有两点A(﹣1,2),B(3,2),C是坐标轴上的一点,若△ABC是直角三角形,则满足条件的点C有(??
)
A.?3个???????????????????????????????????????B.?4个???????????????????????????????????????C.?5个???????????????????????????????????????D.?6个
4.如图,在平面直角坐标系中,
顶点A,B的坐标分别是
,
,
,则顶点C的坐标为(?
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
5.有下列命题中是真命题的为(??
)
A.?有一个角是锐角的三角形是锐角三角形??
B.?三边长为
,
,
的三角形为直角三角形
C.?等腰三角形的高、中线、角平分线互相重合
D.?三角形三边垂直平分线的交点到三角形三个顶点的距离相等
6.一条河的宽度处处相等,小强想从河的南岸横游到北岸去,由于水流影响,小强上岸地点偏离目标地点200m,他在水中实际游了520m,那么该河的宽度为(?
)
A.?440m??????????????????????????????????B.?460m??????????????????????????????????C.?480m??????????????????????????????????D.?500m
7.已知三角形的三边a,b,c满足
,则△ABC是(??
)
A.?等腰三角形?????????????B.?等腰直角三角形?????????????C.?等边三角形?????????????D.?等腰三角形或直角三角形
8.平面直角坐标系中,点P(2,0)平移后对应的点为Q(5,4),则平移的距离为(??
)
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?7
9.有一个直角三角形的两边长分别为3和4,则第三边的长为(?
)
A.?5??????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?5或
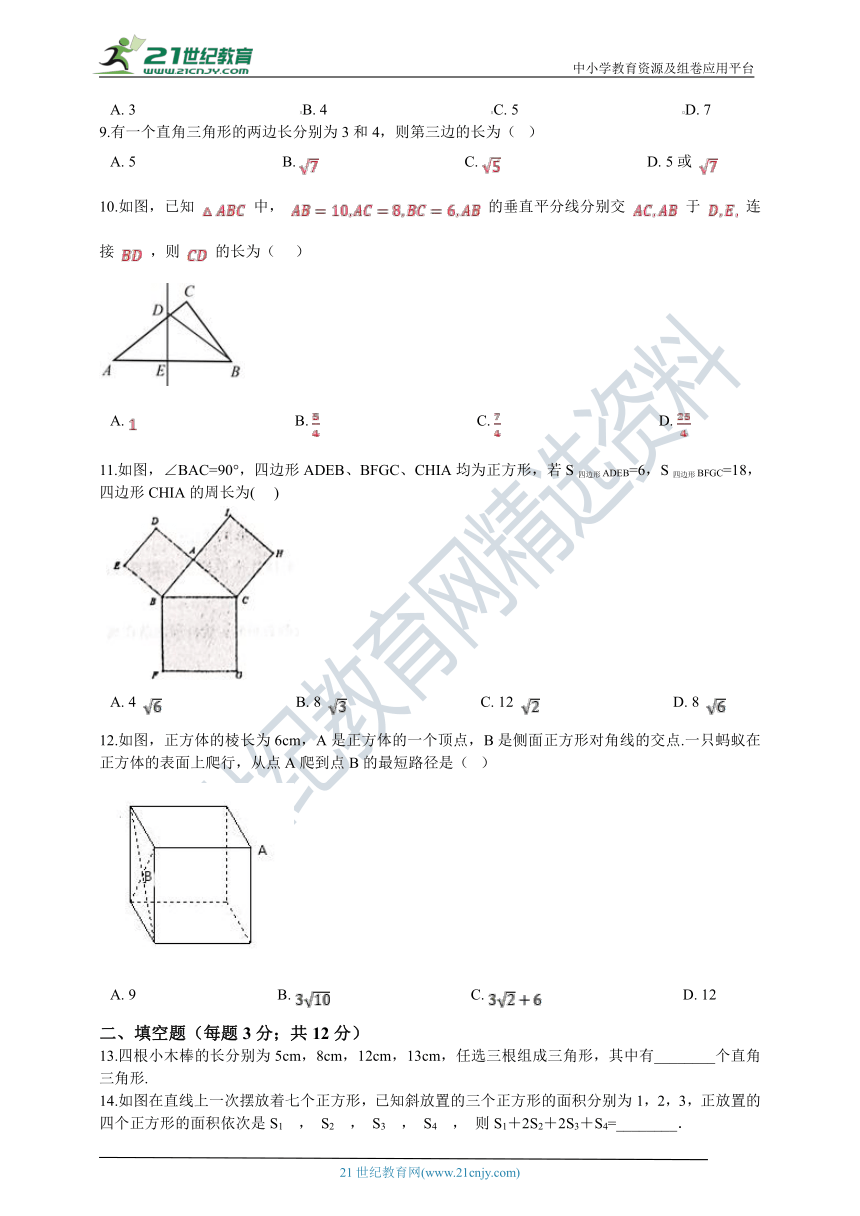
10.如图,已知
中,
的垂直平分线分别交
于
连接
,则
的长为(???
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
11.如图,∠BAC=90°,四边形ADEB、BFGC、CHIA均为正方形,若S四边形ADEB=6,S四边形BFGC=18,四边形CHIA的周长为(???
)
A.?4
???????????????????????????????????B.?8
???????????????????????????????????C.?12
???????????????????????????????????D.?8
12.如图,正方体的棱长为6cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是(?
)
A.?9?????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?12
二、填空题(每题3分;共12分)
13.四根小木棒的长分别为5cm,8cm,12cm,13cm,任选三根组成三角形,其中有________个直角三角形.
14.如图在直线上一次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积依次是S1
,
S2
,
S3
,
S4
,
则S1+2S2+2S3+S4=________.
15.如图所示的网格是正方形网格,则
________
(点
、
、
、
、
是网格线交点).
16.如图,在四边形ABCD中,∠A=90°AB=AD,E、F分别是AB、AD中点,若EF=
,BC=
,CD=
,则S四边形ABCD=________
三、解答题(共72分)
17(10分).如图,在等腰△ABC中,AB=AC=15,点D是AC边上的一点,且CD=3,BD=9,判断
△ABD的形状,并说明理由
18(10分).如图,在
中,
于点
.求
的长.
19(10分).为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.Okm,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
20(10分).已知a,b,c为△ABC的三边,且满足a2﹣8a+b2﹣2
+|c﹣5|+19=0,试判断△ABC的形状.
21(10分).由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图,其树恰好落在另一棵树乙的根部C处,已知AB=1米,BC=5米,已知两棵树的水平距离为3米,请计算出这棵树原来的高度(结果保留根号)
22(10分).如图,A,B,C,D为矩形的四个顶点,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动,当点P运动到点B停止时,点Q也随之停止运动,问P,Q两点从出发经过几秒时,点P,Q间的距离是10cm?
23(12分).如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是________.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
答案解析部分
一、单选题
1.【答案】
A
2.【答案】
C
3.【答案】
C
4.【答案】
B
5.【答案】
D
6.【答案】
C
7.【答案】
D
8.【答案】
C
9.【答案】
D
10.【答案】
C
11.【答案】
B
12.【答案】
B
二、填空题
13.【答案】
1
14.【答案】
6
15.【答案】
45
16.【答案】
三、解答题
17.【答案】
解:∵AC=15,
CD=3,∴AD=AC-
CD=12
∵BD2+AD2=92+122=225,AB2=152=225.
∴
BD2+AD2=
AB2.
∴△ABD是直角三角形
18.【答案】
解:
即
是直角三角形(勾股定理逆定理)
答:
的长度是
19.【答案】
解:由题意可得:设AE=xkm,则EB=(2.5﹣x)km.∵AC2+AE2=EC2
,
BE2+DB2=ED2
,
EC=DE,∴AC2+AE2=BE2+DB2
,
∴1.52+x2=(2.5﹣x)2+12
,
解得:x=1.
答:图书室E应该建在距点A1km处,才能使它到两所学校的距离相等.
20.【答案】
解:
,
,
,
,
解得
,
,
,
,
,
是钝角三角形.
21.【答案】
解:如图作CD⊥AB交AB延长线于D,
由题意知BC=5,CD=3,
根据勾股定理得:BD=4,
∵AB=1,
∴AD=5,
AC=
?,
∴这棵数原来的高度=1+
?,
答:这棵树原来的高度为(1+
)米.
22.【答案】
10cm
23.【答案】
(1)50°.
(2)解:①∵AN=BN,
∴BN+CN=AN+CN=AC,
∵AB=AC=8cm,
∴BN+CN=8cm,
∵△NBC的周长是14cm.
∴BC=14﹣8=6cm.
②∵A、B关于直线MN对称,
∴连接AC与MN的交点即为所求的P点,此时P和N重合,
即△BNC的周长就是△PBC的周长最小值,
∴△PBC的周长最小值为14cm.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版八年级数学勾股定理逆定理章节测试卷
姓名:
分数:
一、单选题(每题3分;共36分)
1.下列结论中,正确的有(??
)
①△ABC的三边长分别为a,b,c,若b2+c2=a2
,
则△ABC是直角三角形;②在Rt△ABC中,已知两边长分别为6和8,则第三边的长为10;③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;④若三角形的三边长之比为1:2:
,则该三角形是直角三角形.
A.?3个???????????????????????????????????????B.?2个???????????????????????????????????????C.?1个???????????????????????????????????????D.?0个
2.等腰三角形一腰长为5,这一腰上的高为3,则这个等腰三角形底边长为(??
)
A.?????????????????????????????B.?????????????????????????????C.?
或
????????????????????????????D.?4或
3.在平面直角坐标系中有两点A(﹣1,2),B(3,2),C是坐标轴上的一点,若△ABC是直角三角形,则满足条件的点C有(??
)
A.?3个???????????????????????????????????????B.?4个???????????????????????????????????????C.?5个???????????????????????????????????????D.?6个
4.如图,在平面直角坐标系中,
顶点A,B的坐标分别是
,
,
,则顶点C的坐标为(?
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
5.有下列命题中是真命题的为(??
)
A.?有一个角是锐角的三角形是锐角三角形??
B.?三边长为
,
,
的三角形为直角三角形
C.?等腰三角形的高、中线、角平分线互相重合
D.?三角形三边垂直平分线的交点到三角形三个顶点的距离相等
6.一条河的宽度处处相等,小强想从河的南岸横游到北岸去,由于水流影响,小强上岸地点偏离目标地点200m,他在水中实际游了520m,那么该河的宽度为(?
)
A.?440m??????????????????????????????????B.?460m??????????????????????????????????C.?480m??????????????????????????????????D.?500m
7.已知三角形的三边a,b,c满足
,则△ABC是(??
)
A.?等腰三角形?????????????B.?等腰直角三角形?????????????C.?等边三角形?????????????D.?等腰三角形或直角三角形
8.平面直角坐标系中,点P(2,0)平移后对应的点为Q(5,4),则平移的距离为(??
)
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?7
9.有一个直角三角形的两边长分别为3和4,则第三边的长为(?
)
A.?5??????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?5或
10.如图,已知
中,
的垂直平分线分别交
于
连接
,则
的长为(???
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
11.如图,∠BAC=90°,四边形ADEB、BFGC、CHIA均为正方形,若S四边形ADEB=6,S四边形BFGC=18,四边形CHIA的周长为(???
)
A.?4
???????????????????????????????????B.?8
???????????????????????????????????C.?12
???????????????????????????????????D.?8
12.如图,正方体的棱长为6cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是(?
)
A.?9?????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?12
二、填空题(每题3分;共12分)
13.四根小木棒的长分别为5cm,8cm,12cm,13cm,任选三根组成三角形,其中有________个直角三角形.
14.如图在直线上一次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积依次是S1
,
S2
,
S3
,
S4
,
则S1+2S2+2S3+S4=________.
15.如图所示的网格是正方形网格,则
________
(点
、
、
、
、
是网格线交点).
16.如图,在四边形ABCD中,∠A=90°AB=AD,E、F分别是AB、AD中点,若EF=
,BC=
,CD=
,则S四边形ABCD=________
三、解答题(共72分)
17(10分).如图,在等腰△ABC中,AB=AC=15,点D是AC边上的一点,且CD=3,BD=9,判断
△ABD的形状,并说明理由
18(10分).如图,在
中,
于点
.求
的长.
19(10分).为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.Okm,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
20(10分).已知a,b,c为△ABC的三边,且满足a2﹣8a+b2﹣2
+|c﹣5|+19=0,试判断△ABC的形状.
21(10分).由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图,其树恰好落在另一棵树乙的根部C处,已知AB=1米,BC=5米,已知两棵树的水平距离为3米,请计算出这棵树原来的高度(结果保留根号)
22(10分).如图,A,B,C,D为矩形的四个顶点,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动,当点P运动到点B停止时,点Q也随之停止运动,问P,Q两点从出发经过几秒时,点P,Q间的距离是10cm?
23(12分).如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是________.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
答案解析部分
一、单选题
1.【答案】
A
2.【答案】
C
3.【答案】
C
4.【答案】
B
5.【答案】
D
6.【答案】
C
7.【答案】
D
8.【答案】
C
9.【答案】
D
10.【答案】
C
11.【答案】
B
12.【答案】
B
二、填空题
13.【答案】
1
14.【答案】
6
15.【答案】
45
16.【答案】
三、解答题
17.【答案】
解:∵AC=15,
CD=3,∴AD=AC-
CD=12
∵BD2+AD2=92+122=225,AB2=152=225.
∴
BD2+AD2=
AB2.
∴△ABD是直角三角形
18.【答案】
解:
即
是直角三角形(勾股定理逆定理)
答:
的长度是
19.【答案】
解:由题意可得:设AE=xkm,则EB=(2.5﹣x)km.∵AC2+AE2=EC2
,
BE2+DB2=ED2
,
EC=DE,∴AC2+AE2=BE2+DB2
,
∴1.52+x2=(2.5﹣x)2+12
,
解得:x=1.
答:图书室E应该建在距点A1km处,才能使它到两所学校的距离相等.
20.【答案】
解:
,
,
,
,
解得
,
,
,
,
,
是钝角三角形.
21.【答案】
解:如图作CD⊥AB交AB延长线于D,
由题意知BC=5,CD=3,
根据勾股定理得:BD=4,
∵AB=1,
∴AD=5,
AC=
?,
∴这棵数原来的高度=1+
?,
答:这棵树原来的高度为(1+
)米.
22.【答案】
10cm
23.【答案】
(1)50°.
(2)解:①∵AN=BN,
∴BN+CN=AN+CN=AC,
∵AB=AC=8cm,
∴BN+CN=8cm,
∵△NBC的周长是14cm.
∴BC=14﹣8=6cm.
②∵A、B关于直线MN对称,
∴连接AC与MN的交点即为所求的P点,此时P和N重合,
即△BNC的周长就是△PBC的周长最小值,
∴△PBC的周长最小值为14cm.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
