2020—2021学年人教版数学九年级下册27.2.1 相似三角形的判定(共29张ppt)
文档属性
| 名称 | 2020—2021学年人教版数学九年级下册27.2.1 相似三角形的判定(共29张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 07:33:38 | ||
图片预览



文档简介
(共29张PPT)
27.2
相似三角形
27.2.1
相似三角形的判定
(第1课时)
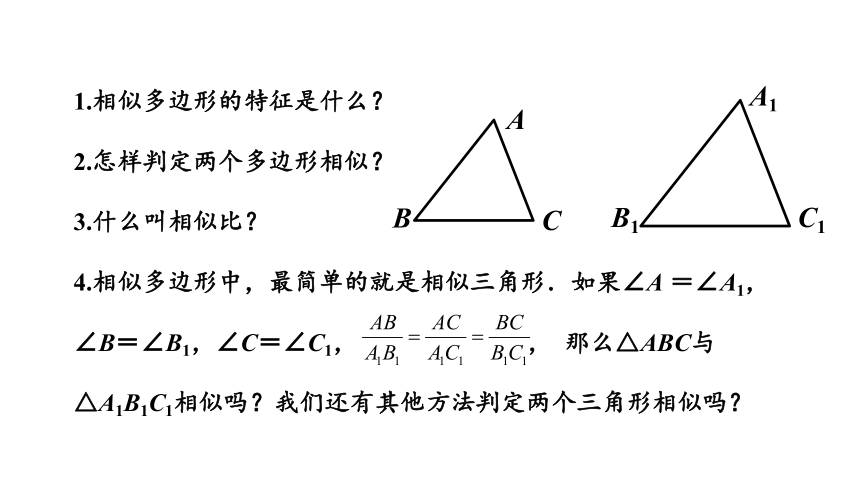
1.相似多边形的特征是什么?
2.怎样判定两个多边形相似?
3.什么叫相似比?
4.相似多边形中,最简单的就是相似三角形.如果∠A
=∠A1,
∠B=∠B1,∠C=∠C1,
,
那么△ABC与
△A1B1C1相似吗?我们还有其他方法判定两个三角形相似吗?
A
B
C
A1
B1
C1
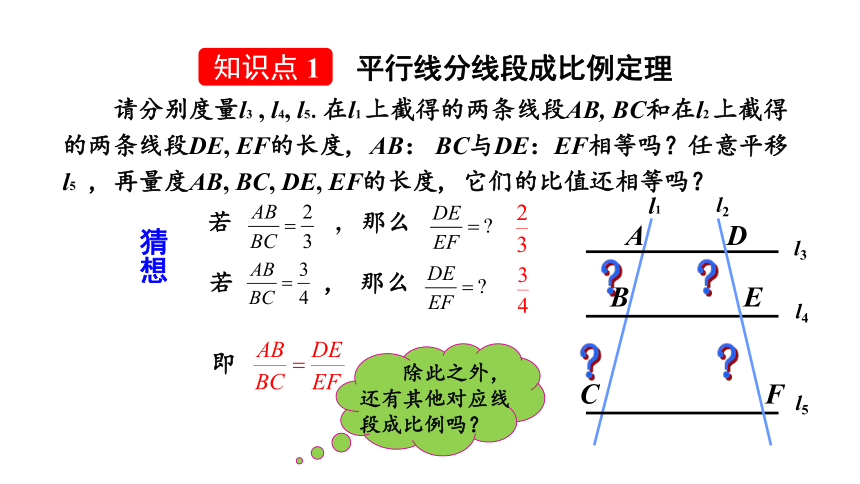
请分别度量l3
,
l4,
l5.在l1
上截得的两条线段AB,
BC和在l2
上截得的两条线段DE,
EF的长度,
AB:
BC与DE:EF相等吗?任意平移l5
,
再量度AB,
BC,
DE,
EF的长度,
它们的比值还相等吗?
?
?
?
?
猜想
A
B
C
D
E
F
l2
l1
除此之外,还有其他对应线段成比例吗?
l2
l3
l4
l5
知识点
1
平行线分线段成比例定理
若
,那么
若
,
那么
即
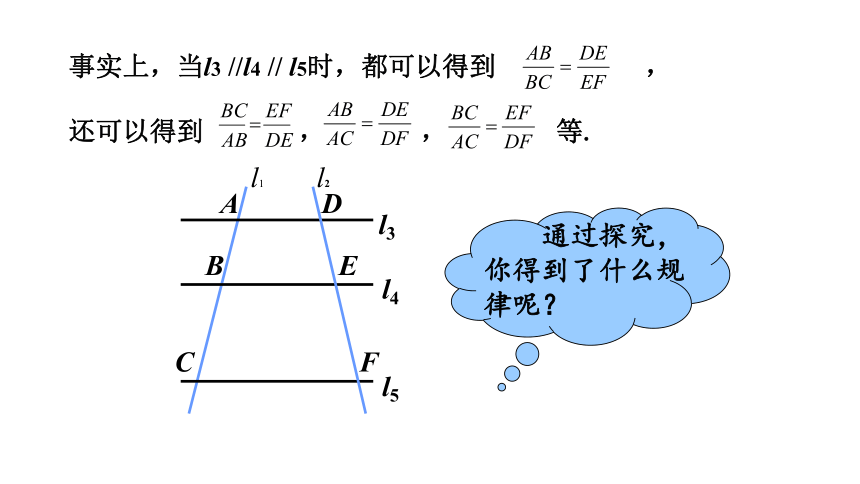
事实上,当l3
//l4
//
l5时,都可以得到
,
还可以得到
,
,
等.
A
B
C
D
E
F
l3
l4
l5
l1
l2
通过探究,你得到了什么规律呢?
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
符号语言:
若a∥b∥
c
,则
,
,
归纳:
A1
A2
A3
B1
B2
B3
b
c
a
1.
如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?
【想一想】
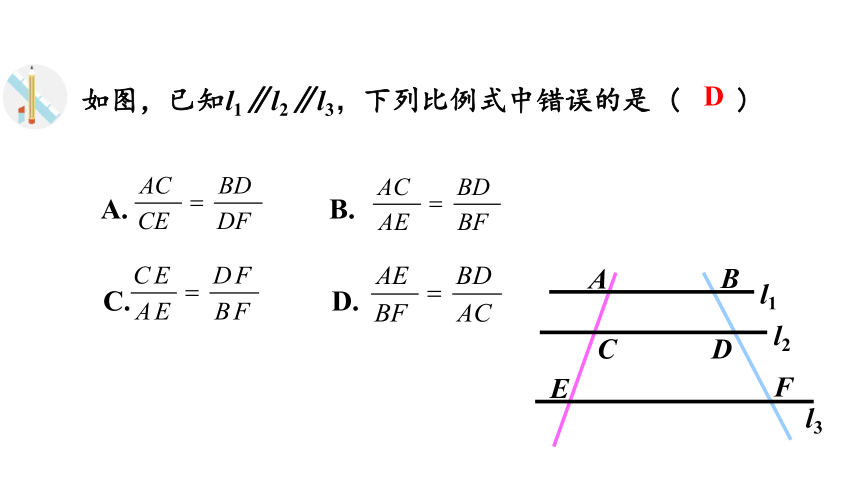
如图,已知l1∥l2∥l3,下列比例式中错误的是
(
)
A.
B.
C.
D.
D
A
C
E
B
D
F
l2
l1
l3
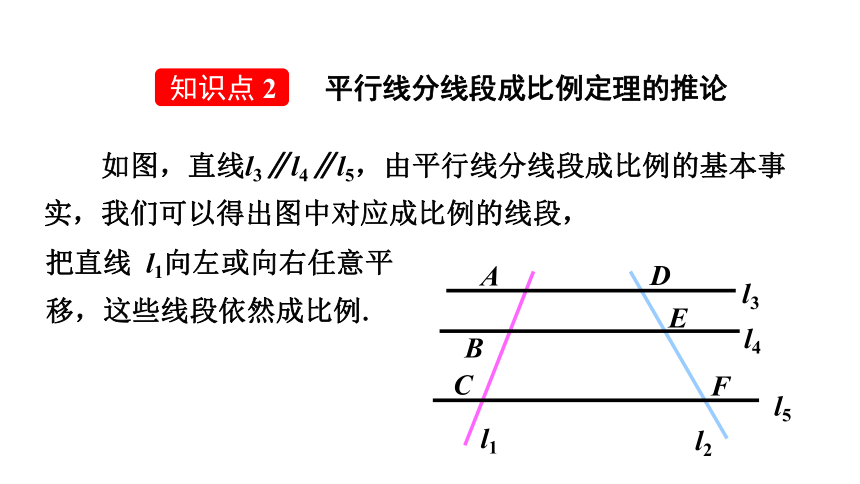
如图,直线l3∥l4∥l5,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,
A
B
C
D
E
F
l4
l5
l1
l2
l3
把直线
l1向左或向右任意平移,这些线段依然成比例.
知识点
2
平行线分线段成比例定理的推论
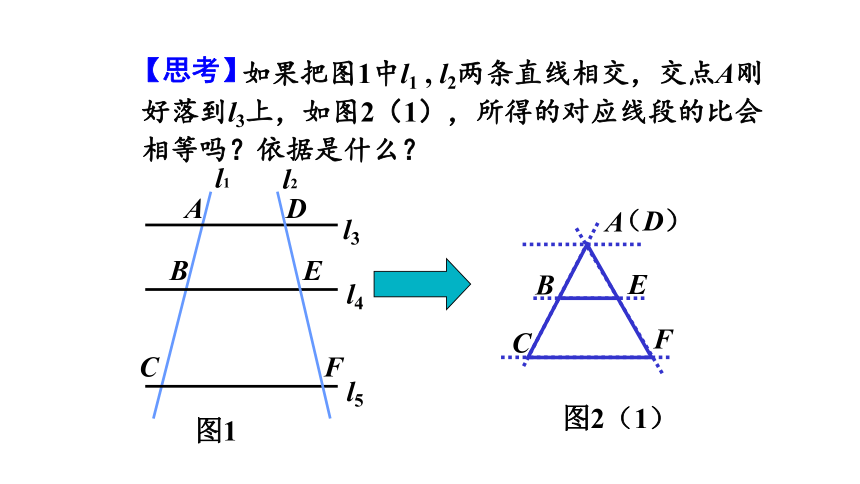
【思考】
如果把图1中l1
,
l2两条直线相交,交点A刚好落到l3上,如图2(1),所得的对应线段的比会相等吗?依据是什么?
A
B
C
D
E
F
l3
l4
l5
l1
l2
图1
图2(1)
A
(D)
E
F
C
B
【思考】如果把图1中l1
,
l2两条直线相交,交点A刚好落到l4上,如图2(2)所得的对应线段的比会相等吗?依据是什么?
图1
图2(2)
A
B
C
D
E
F
l3
l4
l5
l1
l2
B
C
E
A
D
l1
l2
l3
l4
l5
l2
l3
l1
l3
l
l?
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l?
归纳:
如图,l1∥l2∥l3,
,DE=6,求DF的长.
解:∵l1∥l2∥l3,
∴
.
又∵
,DE=6,
∴
,
解得EF=4.
∴DF=DE+EF=6+4=10.
l1
l2
l3
例
如图,在△ABC中,DE∥BC,AC=4
,AB=3,EC=1.求AD和BD.
∴AE=3.
解:∵AC=4,EC=1,
∵
DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
素养考点
1
利用平行线分线段成比例定理及推论求线段长度
如图,在△ABC中,EF∥BC,AE=2cm,
BE=6cm,FC=3cm,AF的长为_______.
1cm
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
问题1
△ADE与△ABC的三个角分别相等吗?
问题2
分别度量△ADE与△ABC的边长,它们的边
长是否对应成比例?
B
C
A
D
E
知识点
3
相似三角形的判定定理
问题3
你认为△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
通过度量,我们发现△ADE∽△ABC,
且只要DE∥BC,这个结论恒成立.
探究新知
B
C
A
D
E
【思考】1.我们通过度量三角形的边长,知道△ADE∽
△ABC,但要用相似的定义去证明它,我们需要证明什么?
2.由前面的结论,我们可以得到什么?还需证明什么?
用相似的定义证明△ADE∽△ABC
B
C
A
D
E
A
B
C
D
E
证明:在△ADE与△ABC中,
∠A=
∠A.
∵
DE//BC,
∴∠ADE=∠B,
∠AED=∠C,
过E作EF//AB交BC于F,
∵四边形DBFE是平行四边形,
F
∴DE=BF
.
∴△ADE∽△ABC
.
∴
.
∴
.
则
已知:如图,在△ABC中,DE//BC,且DE分别交AB
,
AC于点D、E.
求证:△ADE∽△ABC
.
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
定理:平行于三角形一边的直线和其他两边相交,所构成
的三角形与原三角形相似.
符号语言:
∵
DE//BC,
∴△ADE∽△ABC.
【讨论】过点D作与AC平行的直线与BC相交,可否证明△ADE∽△ABC?如果在三角形中出现一边的平行线,那么你应该联想到什么?
【方法总结】过点D作与AC平行的直线与BC相交,仍可证明△ADE∽△ABC,这与教材第31页证法雷同.题目中有平行线,可得相似三角形,然后利用相似三角形的性质,可列出比例式.
已知:如图,AB∥EF∥CD,图中共有___对相似三角形.
3
C
D
A
B
E
F
O
相似具有传递性
A
如图,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,若AD=4,DB=2,则DE:BC的值为( )
A.
B.
C.
D.
1.
如图,在
△ABC
中,EF∥BC,AE=2cm,BE=6cm,BC
=
4
cm,EF
长(
)
A
A
B
C
E
F
A.
1cm
B.
cm
C.
3cm
D.
2cm
A
B
C
E
D
F
G
2.如图,DE∥BC,
,
;
FG∥BC,
,则
.
3.如图,在△ABC中,
EF∥BC.
(
1
)如果E、F分别是
AB
和
AC
上的点,
AE
=
BE=7,
FC
=
4
,那么
AF
的长是多少?
A
B
C
E
F
解:∵
∴
解得
AF
=
4.
(2)
如果AB
=
10,AE=6,AF
=
5,那么
FC
的长是多少?
解:∵
∴
解得
.
A
B
C
E
F
如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.
求证:OD∶OA=OE∶OB
证明:
∵
DF∥AC,
∵
EF∥BC,
如图,已知菱形
ABCD
内接于△AEF,AE=5cm,
AF
=
4
cm,求菱形的边长.
解:∵
四边形
ABCD
为菱形,
B
C
A
D
E
F
∴CD∥AB,
∴
设菱形的边长为
x
cm,则CD
=
AD
=
x
cm,DF
=
(4-x
)cm,
∴
解得
∴菱形的边长为
cm.
两条直线被一组平行线所截,所得的对应线段成比例.
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
相似三角形判定的引理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
基本事实
平行线分线段成比例定理及其推论
27.2
相似三角形
27.2.1
相似三角形的判定
(第1课时)
1.相似多边形的特征是什么?
2.怎样判定两个多边形相似?
3.什么叫相似比?
4.相似多边形中,最简单的就是相似三角形.如果∠A
=∠A1,
∠B=∠B1,∠C=∠C1,
,
那么△ABC与
△A1B1C1相似吗?我们还有其他方法判定两个三角形相似吗?
A
B
C
A1
B1
C1
请分别度量l3
,
l4,
l5.在l1
上截得的两条线段AB,
BC和在l2
上截得的两条线段DE,
EF的长度,
AB:
BC与DE:EF相等吗?任意平移l5
,
再量度AB,
BC,
DE,
EF的长度,
它们的比值还相等吗?
?
?
?
?
猜想
A
B
C
D
E
F
l2
l1
除此之外,还有其他对应线段成比例吗?
l2
l3
l4
l5
知识点
1
平行线分线段成比例定理
若
,那么
若
,
那么
即
事实上,当l3
//l4
//
l5时,都可以得到
,
还可以得到
,
,
等.
A
B
C
D
E
F
l3
l4
l5
l1
l2
通过探究,你得到了什么规律呢?
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
符号语言:
若a∥b∥
c
,则
,
,
归纳:
A1
A2
A3
B1
B2
B3
b
c
a
1.
如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?
【想一想】
如图,已知l1∥l2∥l3,下列比例式中错误的是
(
)
A.
B.
C.
D.
D
A
C
E
B
D
F
l2
l1
l3
如图,直线l3∥l4∥l5,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,
A
B
C
D
E
F
l4
l5
l1
l2
l3
把直线
l1向左或向右任意平移,这些线段依然成比例.
知识点
2
平行线分线段成比例定理的推论
【思考】
如果把图1中l1
,
l2两条直线相交,交点A刚好落到l3上,如图2(1),所得的对应线段的比会相等吗?依据是什么?
A
B
C
D
E
F
l3
l4
l5
l1
l2
图1
图2(1)
A
(D)
E
F
C
B
【思考】如果把图1中l1
,
l2两条直线相交,交点A刚好落到l4上,如图2(2)所得的对应线段的比会相等吗?依据是什么?
图1
图2(2)
A
B
C
D
E
F
l3
l4
l5
l1
l2
B
C
E
A
D
l1
l2
l3
l4
l5
l2
l3
l1
l3
l
l?
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l?
归纳:
如图,l1∥l2∥l3,
,DE=6,求DF的长.
解:∵l1∥l2∥l3,
∴
.
又∵
,DE=6,
∴
,
解得EF=4.
∴DF=DE+EF=6+4=10.
l1
l2
l3
例
如图,在△ABC中,DE∥BC,AC=4
,AB=3,EC=1.求AD和BD.
∴AE=3.
解:∵AC=4,EC=1,
∵
DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
素养考点
1
利用平行线分线段成比例定理及推论求线段长度
如图,在△ABC中,EF∥BC,AE=2cm,
BE=6cm,FC=3cm,AF的长为_______.
1cm
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
问题1
△ADE与△ABC的三个角分别相等吗?
问题2
分别度量△ADE与△ABC的边长,它们的边
长是否对应成比例?
B
C
A
D
E
知识点
3
相似三角形的判定定理
问题3
你认为△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
通过度量,我们发现△ADE∽△ABC,
且只要DE∥BC,这个结论恒成立.
探究新知
B
C
A
D
E
【思考】1.我们通过度量三角形的边长,知道△ADE∽
△ABC,但要用相似的定义去证明它,我们需要证明什么?
2.由前面的结论,我们可以得到什么?还需证明什么?
用相似的定义证明△ADE∽△ABC
B
C
A
D
E
A
B
C
D
E
证明:在△ADE与△ABC中,
∠A=
∠A.
∵
DE//BC,
∴∠ADE=∠B,
∠AED=∠C,
过E作EF//AB交BC于F,
∵四边形DBFE是平行四边形,
F
∴DE=BF
.
∴△ADE∽△ABC
.
∴
.
∴
.
则
已知:如图,在△ABC中,DE//BC,且DE分别交AB
,
AC于点D、E.
求证:△ADE∽△ABC
.
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
定理:平行于三角形一边的直线和其他两边相交,所构成
的三角形与原三角形相似.
符号语言:
∵
DE//BC,
∴△ADE∽△ABC.
【讨论】过点D作与AC平行的直线与BC相交,可否证明△ADE∽△ABC?如果在三角形中出现一边的平行线,那么你应该联想到什么?
【方法总结】过点D作与AC平行的直线与BC相交,仍可证明△ADE∽△ABC,这与教材第31页证法雷同.题目中有平行线,可得相似三角形,然后利用相似三角形的性质,可列出比例式.
已知:如图,AB∥EF∥CD,图中共有___对相似三角形.
3
C
D
A
B
E
F
O
相似具有传递性
A
如图,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,若AD=4,DB=2,则DE:BC的值为( )
A.
B.
C.
D.
1.
如图,在
△ABC
中,EF∥BC,AE=2cm,BE=6cm,BC
=
4
cm,EF
长(
)
A
A
B
C
E
F
A.
1cm
B.
cm
C.
3cm
D.
2cm
A
B
C
E
D
F
G
2.如图,DE∥BC,
,
;
FG∥BC,
,则
.
3.如图,在△ABC中,
EF∥BC.
(
1
)如果E、F分别是
AB
和
AC
上的点,
AE
=
BE=7,
FC
=
4
,那么
AF
的长是多少?
A
B
C
E
F
解:∵
∴
解得
AF
=
4.
(2)
如果AB
=
10,AE=6,AF
=
5,那么
FC
的长是多少?
解:∵
∴
解得
.
A
B
C
E
F
如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.
求证:OD∶OA=OE∶OB
证明:
∵
DF∥AC,
∵
EF∥BC,
如图,已知菱形
ABCD
内接于△AEF,AE=5cm,
AF
=
4
cm,求菱形的边长.
解:∵
四边形
ABCD
为菱形,
B
C
A
D
E
F
∴CD∥AB,
∴
设菱形的边长为
x
cm,则CD
=
AD
=
x
cm,DF
=
(4-x
)cm,
∴
解得
∴菱形的边长为
cm.
两条直线被一组平行线所截,所得的对应线段成比例.
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
相似三角形判定的引理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
基本事实
平行线分线段成比例定理及其推论
