人教版八年级数学下册第18章《平行四边形》18.1.2 第二课时 平行四边形的判定课件(共21张ppt)
文档属性
| 名称 | 人教版八年级数学下册第18章《平行四边形》18.1.2 第二课时 平行四边形的判定课件(共21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 774.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 07:37:34 | ||
图片预览







文档简介
(共21张PPT)
18.1.2
平行四边形判定
第十八章
平行四边形
第2课时
平行四边形的判定(2)
学习目标
1.知道平行四边形的四种判定方法及推理格式.
2.能用这些判定方法证明一个四边形是平行四边形.
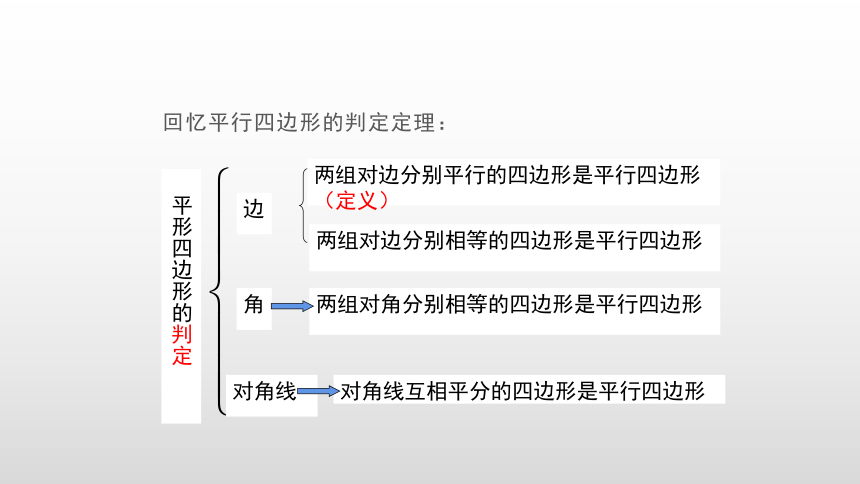
回忆平行四边形的判定定理:
平形四边形的判定
两组对边分别平行的四边形是平行四边形(定义)
边
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
角
对角线
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
只要使互相平行的夹在铁轨之间的枕木长相等就可以了
那这是为什么呢?会不会跟我们学过的平行四边形有关呢?
一组对边平行且相等的四边形
是平行四边形
能否证明
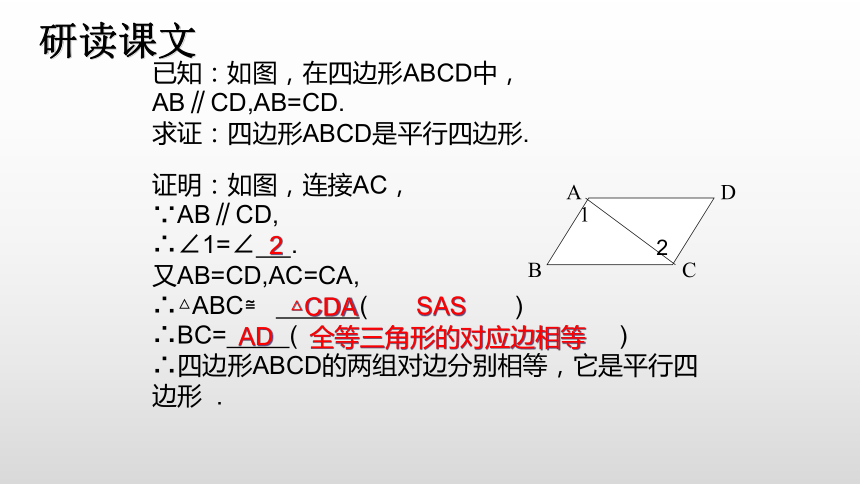
研读课文
已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:如图,连接AC,
∵AB∥CD,
∴∠1=∠
.
又AB=CD,AC=CA,
∴△ABC≌
(
)
∴BC=
(
)
∴四边形ABCD的两组对边分别相等,它是平行四边形
.
A
D
B
C
1
2
2
△CDA
SAS
AD
全等三角形的对应边相等
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
B
D
A
C
如图,在平行四边形ABCD中,E、F分别是边AB、CD的中点,四边形AEFD是平行四边形吗?为什么?
解:四边形AEFD是平行四边形.理由如下:
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
又∵E、F分别是边AB、CD的中点,
∴AE=DF.
又∵AE∥DF,
∴四边形AEFD是平行四边形.
要证四边形是平行四边形,已知有一组对边平行,联想的思路有两种:
一是证明另一组对边平行;
二是证明平行的这组对边相等.
而证明边相等要三角形全等这条思路较常见.
如图,在?
ABCD中,BD是它的一条对角线,过A,C两点分别作AE丄BD,
CF丄BD,E,F为垂足.
求证:四边形AFGE是平行四边形.
例
如图,在
ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:AF=CE.
分析:证AF=CE只需证四边形AECF是平行四边形.
由AE⊥BD,CF⊥BD得AE∥CF.通过证△ABE≌△CDF,得AE=CF,结论即可得证.
随堂演练
1.四边形ABCD中,已知AB∥CD,再添加一个条件_____________,使四边形ABCD是平行四边形.
AB=CD
2.
如图,在
平行四边形
ABCD中,BD是它的一条对线,过A、C两点分别作AE⊥BD,CF⊥BD.E、F为垂足.
求证:四边形AFCE是平行四边形.
A
F
E
D
C
B
3
下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是
平行四边形
D
4.已知:如图,AD∥BC,且AB=CD=5,AC=4,BC=3;
求证:AB∥CD.
C
D
A
B
温馨提示:可利用勾股定理及其逆定理解题
5.如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____;
DP=________;
BQ=________;CQ=________;
6.如图,
ABCD中,线段EF、GH分别在AB、CD上运动,在运动过程中总是保持EF=GH.
(2)若EF=
AB,且S
ABCD=24,
则S四边形EFGH=____.
(1)试猜想四边形EFGH的形状,并说明理由.
通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
回顾与反思
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)对角线互相平分的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)一组对边平行且相等的四边形是平行四边形.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
18.1.2
平行四边形判定
第十八章
平行四边形
第2课时
平行四边形的判定(2)
学习目标
1.知道平行四边形的四种判定方法及推理格式.
2.能用这些判定方法证明一个四边形是平行四边形.
回忆平行四边形的判定定理:
平形四边形的判定
两组对边分别平行的四边形是平行四边形(定义)
边
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
角
对角线
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
只要使互相平行的夹在铁轨之间的枕木长相等就可以了
那这是为什么呢?会不会跟我们学过的平行四边形有关呢?
一组对边平行且相等的四边形
是平行四边形
能否证明
研读课文
已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:如图,连接AC,
∵AB∥CD,
∴∠1=∠
.
又AB=CD,AC=CA,
∴△ABC≌
(
)
∴BC=
(
)
∴四边形ABCD的两组对边分别相等,它是平行四边形
.
A
D
B
C
1
2
2
△CDA
SAS
AD
全等三角形的对应边相等
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
B
D
A
C
如图,在平行四边形ABCD中,E、F分别是边AB、CD的中点,四边形AEFD是平行四边形吗?为什么?
解:四边形AEFD是平行四边形.理由如下:
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
又∵E、F分别是边AB、CD的中点,
∴AE=DF.
又∵AE∥DF,
∴四边形AEFD是平行四边形.
要证四边形是平行四边形,已知有一组对边平行,联想的思路有两种:
一是证明另一组对边平行;
二是证明平行的这组对边相等.
而证明边相等要三角形全等这条思路较常见.
如图,在?
ABCD中,BD是它的一条对角线,过A,C两点分别作AE丄BD,
CF丄BD,E,F为垂足.
求证:四边形AFGE是平行四边形.
例
如图,在
ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:AF=CE.
分析:证AF=CE只需证四边形AECF是平行四边形.
由AE⊥BD,CF⊥BD得AE∥CF.通过证△ABE≌△CDF,得AE=CF,结论即可得证.
随堂演练
1.四边形ABCD中,已知AB∥CD,再添加一个条件_____________,使四边形ABCD是平行四边形.
AB=CD
2.
如图,在
平行四边形
ABCD中,BD是它的一条对线,过A、C两点分别作AE⊥BD,CF⊥BD.E、F为垂足.
求证:四边形AFCE是平行四边形.
A
F
E
D
C
B
3
下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是
平行四边形
D
4.已知:如图,AD∥BC,且AB=CD=5,AC=4,BC=3;
求证:AB∥CD.
C
D
A
B
温馨提示:可利用勾股定理及其逆定理解题
5.如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____;
DP=________;
BQ=________;CQ=________;
6.如图,
ABCD中,线段EF、GH分别在AB、CD上运动,在运动过程中总是保持EF=GH.
(2)若EF=
AB,且S
ABCD=24,
则S四边形EFGH=____.
(1)试猜想四边形EFGH的形状,并说明理由.
通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢?
回顾与反思
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)对角线互相平分的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)一组对边平行且相等的四边形是平行四边形.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
