人教版六年级下册数学—解比例与应用(含答案)
文档属性
| 名称 | 人教版六年级下册数学—解比例与应用(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 339.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 16:19:07 | ||
图片预览

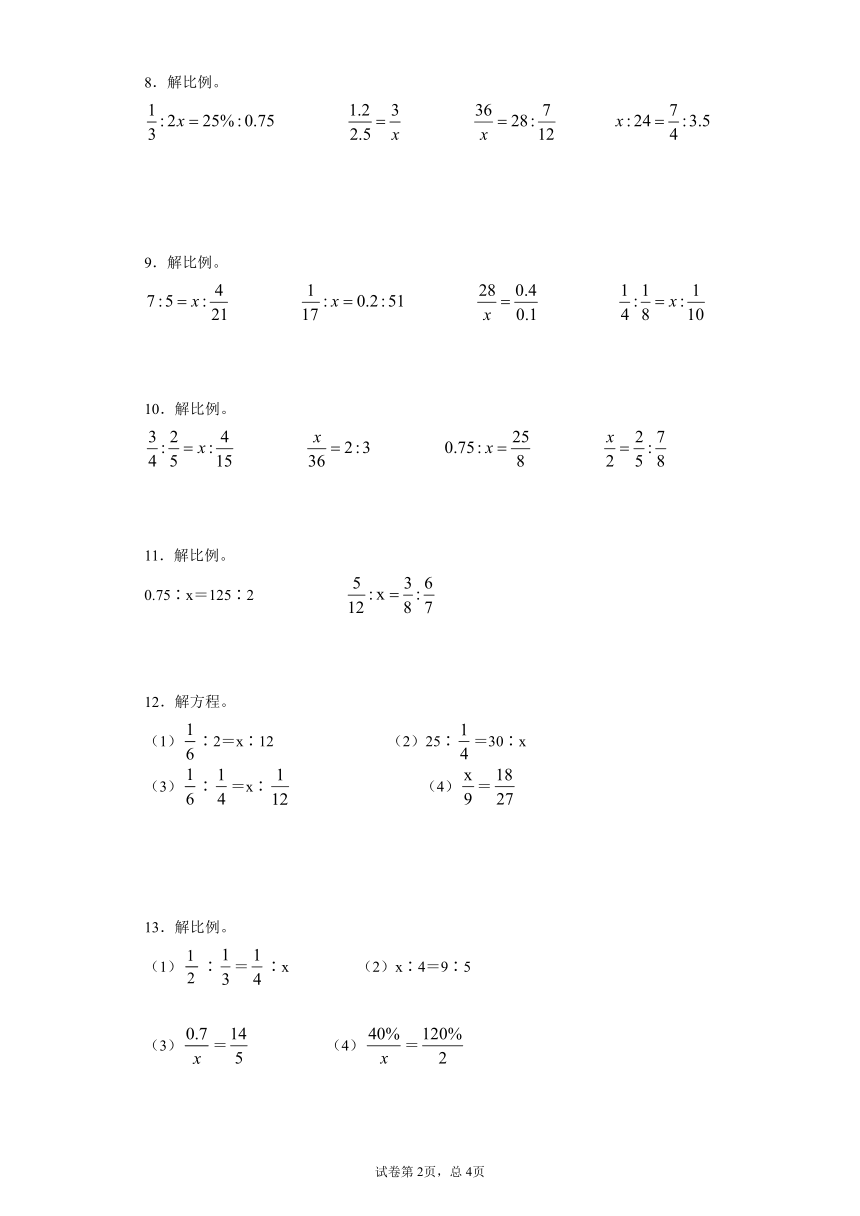



文档简介
六年级下册数学—解比例与应用
姓名:________班级:________学校:_________成绩:___________
一、选择题
1.在2、3、这三个数中插入第四个数x,使得这四个数能组成比例,那么x最小是(
)。
A.
B.
C.
D.
2.图中长方形B的面积是21m2,长方形C的面积是63m2,长方形D的面积是49m2,长方形A的面积是(
)m2.
A.25
B.31
C.29
D.27
二、填空题
3.一个最简分数,如果分子加上1,分子比分母少3;如果分母加上1,则这个分数的分数值是,原分数是(________)。
4.在括号里填上相同的数,使等式成立:。
5.如果(x,y均不为0),那么(________):(________)。
三、解方程或比例
6.解比例。
7.解比例。
8.解比例。
9.解比例。
10.解比例。
11.解比例。
0.75∶x=125∶2
12.解方程。
(1)∶2=x∶12
(2)25∶=30∶x
(3)∶=x∶
(4)=
13.解比例。
(1)∶=∶x
(2)x∶4=9∶5
(3)=
(4)=
14.我会解比例。
15.求未知数。
0.8∶4=∶8
四、解答题
16.一根电线第一次用去与剩下的比是2:3,第二次用去28米,这是剩下与用去的比是1:3,这根电线全长多少米?
17.小李和小王在一次数学测验中,他们的分数比为5:4,如果小李再少得25分,小王再多得25分,那么小李和小王的分数比为5:7,小李和小王原来各得多少分?
18.小明和小华存钱数的比是3:7,如果小明再存入400元,就和小华的存钱一样多.小明原来存了多少钱?
19.相同质量的冰和水的体积比是。现有的水,结成冰后的体积是多少立方分米?
20.有两条纸带,一条长21厘米,一条长13厘米,把两条纸带都剪下同样长的一段以后发现长纸带剩下的长度是短纸带剩下的长度的2倍,问剪下的一段有多长?
21.一个长方形周长是120cm,宽与长的比是1︰4,长方形的长、宽各是多少厘米?面积是多少?
22.某工程队修一条公路,已经修了1800m,已修的长度与未修的长度的比是3:5,这条公路长多少米?
23.根据题意列出比例,并解比例。
2与x的比等于0.7与3.5的比。
24.根据下面的条件列出比例,并解比例。
x和的比等于4和10的比。
25.列出比例,并解比例.
(1)15与x的比等于6与4的比.
(2)x与2的比等于5%与0.6的比.
26.隆兴佳园11号楼的实际高度是38米,它的高度与模型高度的比是500:1.那么模型的高度是多少厘米?
27.有大、小两个圆,大圆直径是8
cm,大圆周长与小圆周长之比是2∶1,求小圆的直径。
28.修一条路,如果每天修120米,8天可以修完;如果每天修150米,几天可以修完?(用比例方法解)
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.C
【分析】
比例的基本性质∶内项之积等于外项之积。要使插入的第四个数x最小,即要使内项之积或外项之积最小,积最小为。据此解答即可。
故答案为:C
2.D
【解析】
试题分析:因为长方形A与长方形C面积比等于高的比;再由长方形B与长方形D面积比等于高的比,由此列出比例,求出长方形A的面积.
解:设长方形A的面积为xm2,则:
x:63=21:49,
49x=63×21,
x=1323÷49,
x=27;
答:长方形A的面积是27m2,
故选D.
点评:解答此题的关键是,在两个长方形的长相等时,面积的比就是长方形的宽的比,由此列出比例解决问题.
3.
【分析】
由分子加1,分子则比分母少3可知,原来分子比分母少1+3=4,如果设原来的分子是x,则分母是x+4,又由分母加1,则分数值等于即可列出方程,由此解答即可。
【详解】
解:设原分数的分子是x,则分母是x+1+3。
4x=3x+15
x=15
15+1+3=19
所以这个分数是
。
【点睛】
找出原来分子和分母之间的关系,再根据分母加1分数值是找等量关系列方程解答即可。
4.7
【分析】
假设括号内填的是x,根据比例的基本性质,列出方程求解即可。
【详解】
设:括号里的数为x;
即括号里填的数字是7。
【点睛】
本题主要考查了分数和比的关系,以及解比例的能力,认真仔细即可。
5.7
3
【分析】
根据比例的基本性质,将转化为外项之积=内项之积的形式,即,两边再同时3y即可。
【详解】
解:
【点睛】
关键是掌握比例的基本性质,比例的两内项积=两外项积。
6.;;
【分析】
根据比例的基本性质,列出内项之积等于外项之积的等式,再解方程。
,根据比例的基本性质,先写成的形式,再根据等式的性质2,两边同时÷8即可;
,根据比例的基本性质,先写成的形式,再根据等式的性质2,两边同时×即可;
,根据比例的基本性质,先写成的形式,再根据等式的性质2,两边同时÷3.6即可。
【详解】
解:
解:
解:
7.x=1;x=7;x=1.6;x=
【分析】
第一题根据比例的基本性质,将其转化为8.4x=21×0.4,再左右两边同时除以8.4即可;
第二题根据比例的基本性质,将其转化为x=×21,再左右两边同时除以即可;
第三题根据比例的基本性质,将其转化为0.1x=0.36×,再左右两边同时除以0.1即可;
第四题根据比例的基本性质,将其转化为x=×21,再左右两边同时除以即可。
【详解】
解:8.4x=21×0.4
8.4x÷8.4=8.4÷8.4
x=1;
解:x=×21
x÷=÷
x=7;
解:0.1x=0.36×
0.1x÷0.1=0.16÷0.1
x=1.6;
解:x=×21
x÷=9÷
x=
8.x=;x=6.25;x=0.75;x=12
【分析】
①先把等号右边的百分数25%和小数0.75分别化为分数,再依据比例的基本性质来解答;
②交叉相乘,转化为乘积式,依据等式性质2,方程左右两边同时除以1.2,得到方程的解;
③先计算等式右边的分数乘整数,再按照除法中各部分的关系来计算;
④依据比例的基本性质,内项之积等于外项之积,转化为乘积式,再应用等式性质2,方程左右两边同时除以3.5,得到方程的解。
【详解】
由分析得:
解:
解:1.2x=3×2.5
1.2x=7.5
x=6.25
解:
解:
9.;;;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时×即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时÷0.2即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时÷0.4即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时×8即可。
【详解】
解:
解:
解:
解:
10.x=;x=24;x=;x=
【分析】
①先依据比例的基本性质,内项之积等于外项之积,将比例式转化为乘积式,再应用等式性质2,方程左右两边同时除以,得到比例的解;
②将等号右边的2∶3改写为,然后交叉相乘,再应用等式性质2,方程左右两边同时除以3,得到比例的解;
③先把0.75改写成分数,再应用比例的基本性质改写成乘积式,最后应用等式性质2,求得比例的解;
④先把等号右边的改写为乘法算式,最后应用等式性质2,方程左右两边同时除以35,求得比例的解。
【详解】
解:
解:x∶36=2∶3
3x=36×2
3x=72
x=24
解:
解:
11.x=0.012;
【分析】
根据比例的基本性质解答即可。
【详解】
0.75∶x=125∶2
解:125x=0.75×2
125x=1.5
125x÷125=1.5÷125
x=0.012;
解:
12.(1)x=1;(2)x=
(3)x=;(4)x=6
【分析】
根据比例的基本性质解方程即可。
【详解】
∶2=x∶12
解:2x=×12
2x=2
x=1;
25∶=30∶x
解:25x=×30
25x=
x=;
∶=x∶
解:x=×
x=;
=
解:27x=18×9
27x=162
x=6
13.(1)x=;(2)x=7.2;
(3)x=0.25;(4)x=
【分析】
(1)∶=∶x,根据比例的基本性质,先写成x=×的形式,两边再同时×2即可;
(2)x∶4=9∶5,根据比例的基本性质,先写成5x=4×9的形式,两边再同时÷5即可;
(3)=,根据比例的基本性质,先写成14x=0.7×5的形式,两边再同时÷14即可;
(4)=,根据比例的基本性质,先写成120%x=40%×2的形式,两边再同时÷1.2即可。
【详解】
(1)∶=∶x
解:x=×
x×2=××2
x=
(2)x∶4=9∶5
解:5x=4×9
5x÷5=4×9÷5
x=7.2
(3)=
解:14x=0.7×5
14x÷14=3.5÷14
x=0.25
(4)=
解:120%x=40%×2
1.2x÷1.2=0.8÷1.2
x=
14.50;19;3.75;
【分析】
应根据比例的基本性质:两外项之积等于两内项之积,先把比例转化成方程的形式,再去求比例的解。
【详解】
解:25×14=7x
解:10.5x=35×5.7
350=7x
10.5x=199.5
x=50
x=19
解:15×14=56x
解:
210=56x
X=3.75
x=
【点睛】
本题考查了学生解比例的方法,还考查了学生计算能力的准确性。
15.x=36;x=1.6;x=3
【分析】
(1)根据等式的性质2,等式左右两边先同时乘以x,再同时除以即可
(2)依据比例的基本性质,先把原式写为:4x=0.8×8,再利用等式的性质2求解即可。
(3)依据比例的基本性质,先把原式写为:3x=12×,再利用等式的性质2求解即可。
【详解】
(1)
解:x=8
x=8÷
x=36
(2)0.8∶4=∶8
解:4x=0.8×8
4x=6.4
x=1.6
(3)
解:3x=12×
3x=9
x=3
【点睛】
掌握等式的性质和比例的基本性质是解题的依据,注意书写格式。
16.80米
【详解】
解:设这根电线全长x米,由题意,得:
(x﹣28):(x+28)=1:3,
由比例的性质,得:
x+28=(x﹣28)×3,
x=28×4,
x=4×4×5,
x=80;
答:这根电线全长80米.
17.小李:100分
小王:80分
【详解】
解:设小王原来的分数为x,则小李原来的分数为x,
(x﹣25):(x+25)=5:7,
(x﹣25)×7=(x+25)×5,
x﹣175=5x+125,
x﹣5x=125+175,
3.75x=300,
x=80;
×80=100(分);
答:小李原来的分数是100分,小王原来的分数是80分.
18.300
【解析】
试题分析:根据题意,小明与小华相差:7﹣3=4份,每份是:400÷4=100元,小明原来有:100×3=300(元).
解:400÷(7﹣3)×3
=100×3
=300(元);
答:小明原来存了300元.
点评:先求出小明与小华相差的份数,再求出每份是多少元,进而解决问题.
19.
【分析】
根据题意可知,相同质量的冰和水的体积比是10∶9,已知水有180L,即体积是180立方分米,如果设结成冰后的体积是x立方分米,那么可以列出比例x∶180=10∶9。求出x的值,也就是结成冰后的体积。
【详解】
解:设结成冰后的体积是。
答:结成冰后的体积是。
【点睛】
本题考查用比例解决问题,解答本题的关键是掌握列比例解决问题的方法。
20.5厘米
【分析】
本题可列方程解答,设剪下的一段有x厘米,则长纸带还剩下21﹣x厘米,短纸带还剩下13﹣x厘米,又知道长纸带剩下的长度是短纸带剩下的长度的2倍,由此可得方程=2,解此方程即可。
【详解】
解:设剪下的一段有x厘米,可得方程:
=2
21﹣x=2×(13﹣x)
x=5
答:剪下的一段有5厘米长。
【点睛】
通过设未知数,根据已知条件列出等量关系式是完成本题的关键。
21.长48厘米,宽12厘米,面积576平方厘米
【解析】
【详解】
解:设长方形的宽是x厘米.
(x+4x)×2=120
x=12
4×12=48
12×48=576
答:长方形的长是48厘米,宽是12厘米,面积是576平方厘米.
22.4800米
【解析】
【详解】
解:设这条公路长xm。
1800:x=3:(5+3)
x=4800
23.2∶x=0.7∶3.5
x=10
【解析】
【详解】
根据已知条件先写出两个比,再用等号连接,最后再利用比例的基本性质解比例。
24.
【解析】
【详解】
x:=4:10
x=
25.(1)15∶x=6∶4,x=10;(2)x∶2=5%∶0.6,x=
【解析】
【详解】
(1)15∶x=6∶4
解:6x=15×4
x=15×4÷6
x=10
(2)x∶2=5%∶0.6
解:0.6x=2×5%
x=2×5%÷0.6
x=
26.7.6厘米
【解析】
试题分析:根据实际高度与模型高的比是500:1,知道实际高度与模型高度的比值一定,所以实际高度与模型高度成正比例,由此列出比例解答即可.
解:设模型的高度是x厘米,得:38米=3800厘米
3800:x=500:1
500x=3800×1
x=7.6
答:模型的高度是7.6厘米.
27.4
厘米
【解析】
【分析】
用方程来解决问题。设小圆的直径为x
cm,再根据已知条件分别表示出大圆和小圆的周长以及它们的比,列出比例式,并根据比例的基本性质解比例,最后写出答。
【详解】
解:设小圆的直径为x
cm。
(8π):(xπ)=2:1
8:x=2:1
x=4
答:小圆的直径为4
厘米。
28.6.4天
【解析】
略
答案第1页,总2页
答案第1页,总2页
姓名:________班级:________学校:_________成绩:___________
一、选择题
1.在2、3、这三个数中插入第四个数x,使得这四个数能组成比例,那么x最小是(
)。
A.
B.
C.
D.
2.图中长方形B的面积是21m2,长方形C的面积是63m2,长方形D的面积是49m2,长方形A的面积是(
)m2.
A.25
B.31
C.29
D.27
二、填空题
3.一个最简分数,如果分子加上1,分子比分母少3;如果分母加上1,则这个分数的分数值是,原分数是(________)。
4.在括号里填上相同的数,使等式成立:。
5.如果(x,y均不为0),那么(________):(________)。
三、解方程或比例
6.解比例。
7.解比例。
8.解比例。
9.解比例。
10.解比例。
11.解比例。
0.75∶x=125∶2
12.解方程。
(1)∶2=x∶12
(2)25∶=30∶x
(3)∶=x∶
(4)=
13.解比例。
(1)∶=∶x
(2)x∶4=9∶5
(3)=
(4)=
14.我会解比例。
15.求未知数。
0.8∶4=∶8
四、解答题
16.一根电线第一次用去与剩下的比是2:3,第二次用去28米,这是剩下与用去的比是1:3,这根电线全长多少米?
17.小李和小王在一次数学测验中,他们的分数比为5:4,如果小李再少得25分,小王再多得25分,那么小李和小王的分数比为5:7,小李和小王原来各得多少分?
18.小明和小华存钱数的比是3:7,如果小明再存入400元,就和小华的存钱一样多.小明原来存了多少钱?
19.相同质量的冰和水的体积比是。现有的水,结成冰后的体积是多少立方分米?
20.有两条纸带,一条长21厘米,一条长13厘米,把两条纸带都剪下同样长的一段以后发现长纸带剩下的长度是短纸带剩下的长度的2倍,问剪下的一段有多长?
21.一个长方形周长是120cm,宽与长的比是1︰4,长方形的长、宽各是多少厘米?面积是多少?
22.某工程队修一条公路,已经修了1800m,已修的长度与未修的长度的比是3:5,这条公路长多少米?
23.根据题意列出比例,并解比例。
2与x的比等于0.7与3.5的比。
24.根据下面的条件列出比例,并解比例。
x和的比等于4和10的比。
25.列出比例,并解比例.
(1)15与x的比等于6与4的比.
(2)x与2的比等于5%与0.6的比.
26.隆兴佳园11号楼的实际高度是38米,它的高度与模型高度的比是500:1.那么模型的高度是多少厘米?
27.有大、小两个圆,大圆直径是8
cm,大圆周长与小圆周长之比是2∶1,求小圆的直径。
28.修一条路,如果每天修120米,8天可以修完;如果每天修150米,几天可以修完?(用比例方法解)
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.C
【分析】
比例的基本性质∶内项之积等于外项之积。要使插入的第四个数x最小,即要使内项之积或外项之积最小,积最小为。据此解答即可。
故答案为:C
2.D
【解析】
试题分析:因为长方形A与长方形C面积比等于高的比;再由长方形B与长方形D面积比等于高的比,由此列出比例,求出长方形A的面积.
解:设长方形A的面积为xm2,则:
x:63=21:49,
49x=63×21,
x=1323÷49,
x=27;
答:长方形A的面积是27m2,
故选D.
点评:解答此题的关键是,在两个长方形的长相等时,面积的比就是长方形的宽的比,由此列出比例解决问题.
3.
【分析】
由分子加1,分子则比分母少3可知,原来分子比分母少1+3=4,如果设原来的分子是x,则分母是x+4,又由分母加1,则分数值等于即可列出方程,由此解答即可。
【详解】
解:设原分数的分子是x,则分母是x+1+3。
4x=3x+15
x=15
15+1+3=19
所以这个分数是
。
【点睛】
找出原来分子和分母之间的关系,再根据分母加1分数值是找等量关系列方程解答即可。
4.7
【分析】
假设括号内填的是x,根据比例的基本性质,列出方程求解即可。
【详解】
设:括号里的数为x;
即括号里填的数字是7。
【点睛】
本题主要考查了分数和比的关系,以及解比例的能力,认真仔细即可。
5.7
3
【分析】
根据比例的基本性质,将转化为外项之积=内项之积的形式,即,两边再同时3y即可。
【详解】
解:
【点睛】
关键是掌握比例的基本性质,比例的两内项积=两外项积。
6.;;
【分析】
根据比例的基本性质,列出内项之积等于外项之积的等式,再解方程。
,根据比例的基本性质,先写成的形式,再根据等式的性质2,两边同时÷8即可;
,根据比例的基本性质,先写成的形式,再根据等式的性质2,两边同时×即可;
,根据比例的基本性质,先写成的形式,再根据等式的性质2,两边同时÷3.6即可。
【详解】
解:
解:
解:
7.x=1;x=7;x=1.6;x=
【分析】
第一题根据比例的基本性质,将其转化为8.4x=21×0.4,再左右两边同时除以8.4即可;
第二题根据比例的基本性质,将其转化为x=×21,再左右两边同时除以即可;
第三题根据比例的基本性质,将其转化为0.1x=0.36×,再左右两边同时除以0.1即可;
第四题根据比例的基本性质,将其转化为x=×21,再左右两边同时除以即可。
【详解】
解:8.4x=21×0.4
8.4x÷8.4=8.4÷8.4
x=1;
解:x=×21
x÷=÷
x=7;
解:0.1x=0.36×
0.1x÷0.1=0.16÷0.1
x=1.6;
解:x=×21
x÷=9÷
x=
8.x=;x=6.25;x=0.75;x=12
【分析】
①先把等号右边的百分数25%和小数0.75分别化为分数,再依据比例的基本性质来解答;
②交叉相乘,转化为乘积式,依据等式性质2,方程左右两边同时除以1.2,得到方程的解;
③先计算等式右边的分数乘整数,再按照除法中各部分的关系来计算;
④依据比例的基本性质,内项之积等于外项之积,转化为乘积式,再应用等式性质2,方程左右两边同时除以3.5,得到方程的解。
【详解】
由分析得:
解:
解:1.2x=3×2.5
1.2x=7.5
x=6.25
解:
解:
9.;;;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时×即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时÷0.2即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时÷0.4即可;
,根据比例的基本性质,写成的形式,再根据等式的性质2,两边同时×8即可。
【详解】
解:
解:
解:
解:
10.x=;x=24;x=;x=
【分析】
①先依据比例的基本性质,内项之积等于外项之积,将比例式转化为乘积式,再应用等式性质2,方程左右两边同时除以,得到比例的解;
②将等号右边的2∶3改写为,然后交叉相乘,再应用等式性质2,方程左右两边同时除以3,得到比例的解;
③先把0.75改写成分数,再应用比例的基本性质改写成乘积式,最后应用等式性质2,求得比例的解;
④先把等号右边的改写为乘法算式,最后应用等式性质2,方程左右两边同时除以35,求得比例的解。
【详解】
解:
解:x∶36=2∶3
3x=36×2
3x=72
x=24
解:
解:
11.x=0.012;
【分析】
根据比例的基本性质解答即可。
【详解】
0.75∶x=125∶2
解:125x=0.75×2
125x=1.5
125x÷125=1.5÷125
x=0.012;
解:
12.(1)x=1;(2)x=
(3)x=;(4)x=6
【分析】
根据比例的基本性质解方程即可。
【详解】
∶2=x∶12
解:2x=×12
2x=2
x=1;
25∶=30∶x
解:25x=×30
25x=
x=;
∶=x∶
解:x=×
x=;
=
解:27x=18×9
27x=162
x=6
13.(1)x=;(2)x=7.2;
(3)x=0.25;(4)x=
【分析】
(1)∶=∶x,根据比例的基本性质,先写成x=×的形式,两边再同时×2即可;
(2)x∶4=9∶5,根据比例的基本性质,先写成5x=4×9的形式,两边再同时÷5即可;
(3)=,根据比例的基本性质,先写成14x=0.7×5的形式,两边再同时÷14即可;
(4)=,根据比例的基本性质,先写成120%x=40%×2的形式,两边再同时÷1.2即可。
【详解】
(1)∶=∶x
解:x=×
x×2=××2
x=
(2)x∶4=9∶5
解:5x=4×9
5x÷5=4×9÷5
x=7.2
(3)=
解:14x=0.7×5
14x÷14=3.5÷14
x=0.25
(4)=
解:120%x=40%×2
1.2x÷1.2=0.8÷1.2
x=
14.50;19;3.75;
【分析】
应根据比例的基本性质:两外项之积等于两内项之积,先把比例转化成方程的形式,再去求比例的解。
【详解】
解:25×14=7x
解:10.5x=35×5.7
350=7x
10.5x=199.5
x=50
x=19
解:15×14=56x
解:
210=56x
X=3.75
x=
【点睛】
本题考查了学生解比例的方法,还考查了学生计算能力的准确性。
15.x=36;x=1.6;x=3
【分析】
(1)根据等式的性质2,等式左右两边先同时乘以x,再同时除以即可
(2)依据比例的基本性质,先把原式写为:4x=0.8×8,再利用等式的性质2求解即可。
(3)依据比例的基本性质,先把原式写为:3x=12×,再利用等式的性质2求解即可。
【详解】
(1)
解:x=8
x=8÷
x=36
(2)0.8∶4=∶8
解:4x=0.8×8
4x=6.4
x=1.6
(3)
解:3x=12×
3x=9
x=3
【点睛】
掌握等式的性质和比例的基本性质是解题的依据,注意书写格式。
16.80米
【详解】
解:设这根电线全长x米,由题意,得:
(x﹣28):(x+28)=1:3,
由比例的性质,得:
x+28=(x﹣28)×3,
x=28×4,
x=4×4×5,
x=80;
答:这根电线全长80米.
17.小李:100分
小王:80分
【详解】
解:设小王原来的分数为x,则小李原来的分数为x,
(x﹣25):(x+25)=5:7,
(x﹣25)×7=(x+25)×5,
x﹣175=5x+125,
x﹣5x=125+175,
3.75x=300,
x=80;
×80=100(分);
答:小李原来的分数是100分,小王原来的分数是80分.
18.300
【解析】
试题分析:根据题意,小明与小华相差:7﹣3=4份,每份是:400÷4=100元,小明原来有:100×3=300(元).
解:400÷(7﹣3)×3
=100×3
=300(元);
答:小明原来存了300元.
点评:先求出小明与小华相差的份数,再求出每份是多少元,进而解决问题.
19.
【分析】
根据题意可知,相同质量的冰和水的体积比是10∶9,已知水有180L,即体积是180立方分米,如果设结成冰后的体积是x立方分米,那么可以列出比例x∶180=10∶9。求出x的值,也就是结成冰后的体积。
【详解】
解:设结成冰后的体积是。
答:结成冰后的体积是。
【点睛】
本题考查用比例解决问题,解答本题的关键是掌握列比例解决问题的方法。
20.5厘米
【分析】
本题可列方程解答,设剪下的一段有x厘米,则长纸带还剩下21﹣x厘米,短纸带还剩下13﹣x厘米,又知道长纸带剩下的长度是短纸带剩下的长度的2倍,由此可得方程=2,解此方程即可。
【详解】
解:设剪下的一段有x厘米,可得方程:
=2
21﹣x=2×(13﹣x)
x=5
答:剪下的一段有5厘米长。
【点睛】
通过设未知数,根据已知条件列出等量关系式是完成本题的关键。
21.长48厘米,宽12厘米,面积576平方厘米
【解析】
【详解】
解:设长方形的宽是x厘米.
(x+4x)×2=120
x=12
4×12=48
12×48=576
答:长方形的长是48厘米,宽是12厘米,面积是576平方厘米.
22.4800米
【解析】
【详解】
解:设这条公路长xm。
1800:x=3:(5+3)
x=4800
23.2∶x=0.7∶3.5
x=10
【解析】
【详解】
根据已知条件先写出两个比,再用等号连接,最后再利用比例的基本性质解比例。
24.
【解析】
【详解】
x:=4:10
x=
25.(1)15∶x=6∶4,x=10;(2)x∶2=5%∶0.6,x=
【解析】
【详解】
(1)15∶x=6∶4
解:6x=15×4
x=15×4÷6
x=10
(2)x∶2=5%∶0.6
解:0.6x=2×5%
x=2×5%÷0.6
x=
26.7.6厘米
【解析】
试题分析:根据实际高度与模型高的比是500:1,知道实际高度与模型高度的比值一定,所以实际高度与模型高度成正比例,由此列出比例解答即可.
解:设模型的高度是x厘米,得:38米=3800厘米
3800:x=500:1
500x=3800×1
x=7.6
答:模型的高度是7.6厘米.
27.4
厘米
【解析】
【分析】
用方程来解决问题。设小圆的直径为x
cm,再根据已知条件分别表示出大圆和小圆的周长以及它们的比,列出比例式,并根据比例的基本性质解比例,最后写出答。
【详解】
解:设小圆的直径为x
cm。
(8π):(xπ)=2:1
8:x=2:1
x=4
答:小圆的直径为4
厘米。
28.6.4天
【解析】
略
答案第1页,总2页
答案第1页,总2页
