3.2圆的对称性2(无答案)
图片预览
文档简介
圆的对称性
一、例题讲解:
【例1】已知A,B是⊙O上的两点,∠AOB=1200,C是 的中点,试确定四边形OACB的形状,并说明理由.
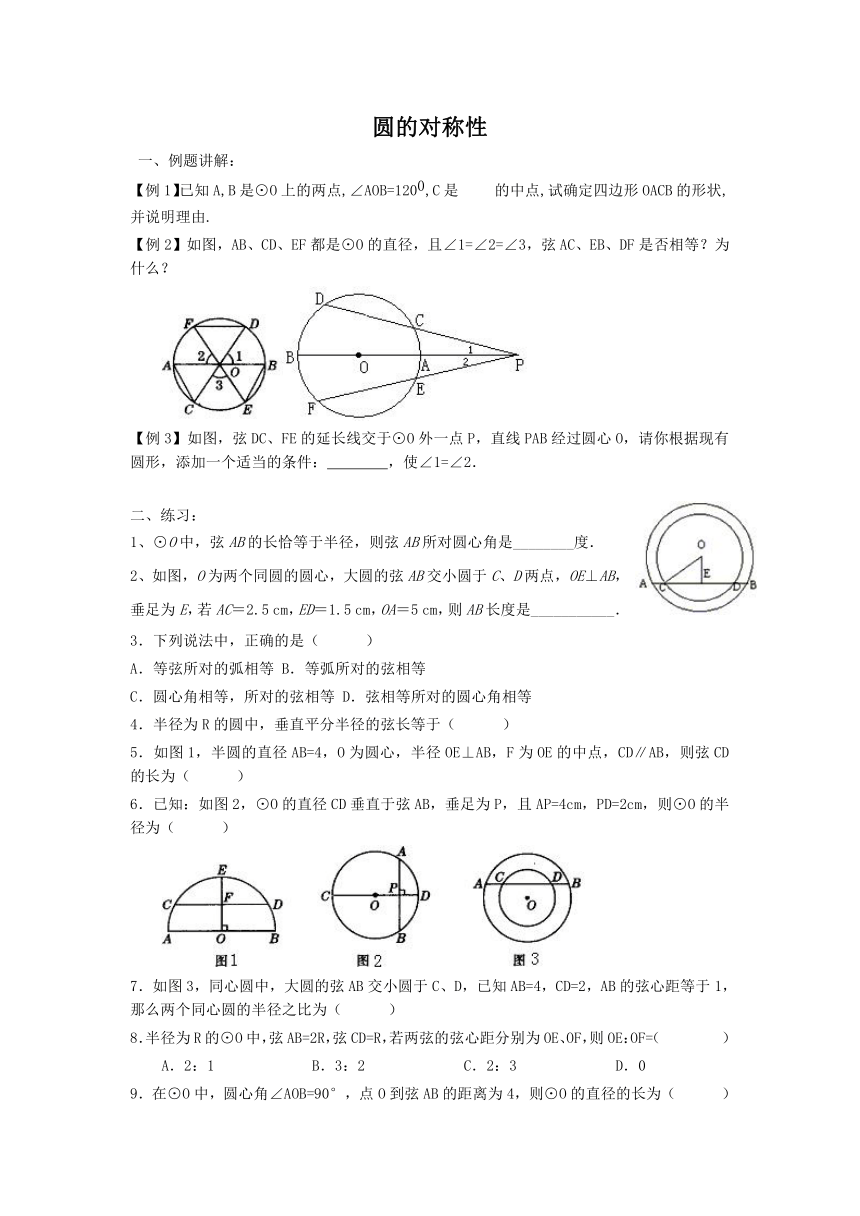
【例2】如图,AB、CD、EF都是⊙O的直径,且∠1=∠2=∠3,弦AC、EB、DF是否相等?为什么?
【例3】如图,弦DC、FE的延长线交于⊙O外一点P,直线PAB经过圆心O,请你根据现有圆形,添加一个适当的条件: ,使∠1=∠2.
二、练习:
1、⊙O中,弦AB的长恰等于半径,则弦AB所对圆心角是________度.
2、如图,O为两个同圆的圆心,大圆的弦AB交小圆于C、D两点,OE⊥AB,垂足为E,若AC=2.5 cm,ED=1.5 cm,OA=5 cm,则AB长度是___________.
3.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
4.半径为R的圆中,垂直平分半径的弦长等于( )
5.如图1,半圆的直径AB=4,O为圆心,半径OE⊥AB,F为OE的中点,CD∥AB,则弦CD的长为( )
6.已知:如图2,⊙O的直径CD垂直于弦AB,垂足为P,且AP=4cm,PD=2cm,则⊙O的半径为( )
7.如图3,同心圆中,大圆的弦AB交小圆于C、D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为( )
8.半径为R的⊙O中,弦AB=2R,弦CD=R,若两弦的弦心距分别为OE、OF,则OE:OF=( )
A.2:1 B.3:2 C.2:3 D.0
9.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为( )
A.4 B.8 C.24 D.16
10.⊙O中若直径为25cm,弦AB的弦心距为10cm,则弦AB的长为 .
11.若圆的半径为2cm,圆中的一条弦长2cm,则此弦中点到此弦所对劣弧的中点的距离为 .
12.AB为圆O的直径,弦CD⊥AB于E,且CD=6cm,OE=4cm,则AB= .
13.半径为5的⊙O内有一点P,且OP=4,则过点P的最短的弦长是 ,最长的弦长是 .
14.弓形的弦长6cm,高为1cm,则弓形所在圆的半径为 cm.
15.在半径为6cm的圆中,垂直平分半径的弦长为 cm.
16.一条弦把圆分成1:3两部分,则弦所对的圆心角为 .
17.弦心距是弦的一半时,弦与直径的比是 ,弦所对的圆心角是 .
18.如图4,AB、CD是⊙O的直径OE⊥AB,OF⊥CD,则∠EOD ∠BOF, ,AC AE.
19.如图5,AB为⊙O的弦,P是AB上一点,AB=10cm,OP=5cm,PA=4cm,求⊙O的半径.
20.如图6,已知以点O为公共圆心的两个同心圆,大圆的弦AB交小圆于C、D.
(1)求证:AC=DB;
(2)如果AB=6cm,CD=4cm,求圆环的面积.
21.⊙O的直径为50cm,弦AB∥CD,且AB=40cm,CD=48cm,求弦AB和CD之间的距离.
22.已知一弓形的弦长为4,弓形所在的圆的半径为7,求弓形的高.
23.如图,已知⊙O1和⊙O2是等圆,直线CF顺次交这两个圆于C、D、E、F,且CF交O1O2于点M,,O1M和O2M相等吗?为什么?
一、例题讲解:
【例1】已知A,B是⊙O上的两点,∠AOB=1200,C是 的中点,试确定四边形OACB的形状,并说明理由.
【例2】如图,AB、CD、EF都是⊙O的直径,且∠1=∠2=∠3,弦AC、EB、DF是否相等?为什么?
【例3】如图,弦DC、FE的延长线交于⊙O外一点P,直线PAB经过圆心O,请你根据现有圆形,添加一个适当的条件: ,使∠1=∠2.
二、练习:
1、⊙O中,弦AB的长恰等于半径,则弦AB所对圆心角是________度.
2、如图,O为两个同圆的圆心,大圆的弦AB交小圆于C、D两点,OE⊥AB,垂足为E,若AC=2.5 cm,ED=1.5 cm,OA=5 cm,则AB长度是___________.
3.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
4.半径为R的圆中,垂直平分半径的弦长等于( )
5.如图1,半圆的直径AB=4,O为圆心,半径OE⊥AB,F为OE的中点,CD∥AB,则弦CD的长为( )
6.已知:如图2,⊙O的直径CD垂直于弦AB,垂足为P,且AP=4cm,PD=2cm,则⊙O的半径为( )
7.如图3,同心圆中,大圆的弦AB交小圆于C、D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为( )
8.半径为R的⊙O中,弦AB=2R,弦CD=R,若两弦的弦心距分别为OE、OF,则OE:OF=( )
A.2:1 B.3:2 C.2:3 D.0
9.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为( )
A.4 B.8 C.24 D.16
10.⊙O中若直径为25cm,弦AB的弦心距为10cm,则弦AB的长为 .
11.若圆的半径为2cm,圆中的一条弦长2cm,则此弦中点到此弦所对劣弧的中点的距离为 .
12.AB为圆O的直径,弦CD⊥AB于E,且CD=6cm,OE=4cm,则AB= .
13.半径为5的⊙O内有一点P,且OP=4,则过点P的最短的弦长是 ,最长的弦长是 .
14.弓形的弦长6cm,高为1cm,则弓形所在圆的半径为 cm.
15.在半径为6cm的圆中,垂直平分半径的弦长为 cm.
16.一条弦把圆分成1:3两部分,则弦所对的圆心角为 .
17.弦心距是弦的一半时,弦与直径的比是 ,弦所对的圆心角是 .
18.如图4,AB、CD是⊙O的直径OE⊥AB,OF⊥CD,则∠EOD ∠BOF, ,AC AE.
19.如图5,AB为⊙O的弦,P是AB上一点,AB=10cm,OP=5cm,PA=4cm,求⊙O的半径.
20.如图6,已知以点O为公共圆心的两个同心圆,大圆的弦AB交小圆于C、D.
(1)求证:AC=DB;
(2)如果AB=6cm,CD=4cm,求圆环的面积.
21.⊙O的直径为50cm,弦AB∥CD,且AB=40cm,CD=48cm,求弦AB和CD之间的距离.
22.已知一弓形的弦长为4,弓形所在的圆的半径为7,求弓形的高.
23.如图,已知⊙O1和⊙O2是等圆,直线CF顺次交这两个圆于C、D、E、F,且CF交O1O2于点M,,O1M和O2M相等吗?为什么?
