第3章 变量之间的关系 单元培优测试卷(Word版 含解析)
文档属性
| 名称 | 第3章 变量之间的关系 单元培优测试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 612.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 17:31:51 | ||
图片预览



文档简介
第3章 变量之间的关系 单元培优测试卷
一、选择题(共10小题).
1.骆驼被称为“沙漠之舟”,它的体温是随时间的变化而变化的,在这一问题中,因变量是( )
A.沙漠 B.体温 C.时间 D.骆驼
2.长方形的周长为24cm,其中一边为xcm(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=12﹣x2 C.y=(12﹣x)?x D.y=2(12﹣x)
3.地表以下的岩层温度y随着所处深度x的变化而变化,在某个地点y与x的关系可以由公式y=35x+20来表示,则y随x的增大而( )
A.增大 B.减小
C.不变 D.以上答案都不对
4.如图所示,OA、BA分别表示甲、乙两名学生运动的路程与时间的关系图象,图中S和t分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快( )
A.2.5m B.2m C.1.5m D.1m
5.表格列出了一项实验的统计数据,表示皮球下落高度d与落下时弹跳高度b的关系,试问下面的哪个式子能表示这种关系(单位cm)( )
d 50 80 100 150
b 25 40 50 75
A.b=d2 B.b=2d C.b=d+25 D.b=
6.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x 0 1 2 3 4 5
y 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0cm
C.物体质量每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为7kg时,弹簧长度为13.5cm
7.在关系式y=3x+5中,下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图象表示;⑤y与x的关系还可以用列表法和图象法表示,其中说法正确的是( )
A.①②⑤ B.①②④ C.①③⑤ D.①④⑤
8.张大伯出去散步,从家走了20min,到了一个离家900m的阅报亭,看了10min报纸后,用了15min返回到家,如图2图象中能表示张大伯离家时间与距离之间关系的是( )
A.
B.
C.
D.
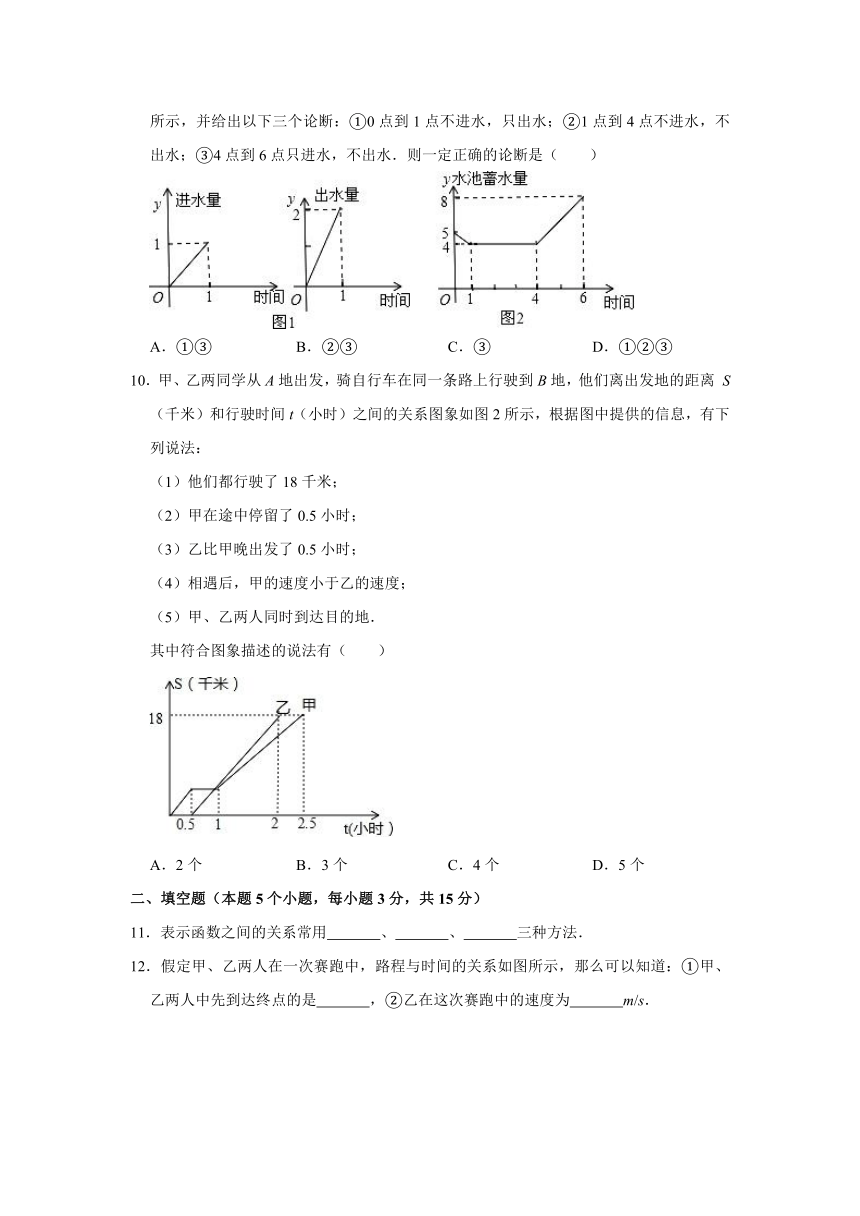
9.为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同)一个进水管和一个出水管的进出水速度如图1所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图2所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则一定正确的论断是( )
A.①③ B.②③ C.③ D.①②③
10.甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离 S(千米)和行驶时间t(小时)之间的关系图象如图2所示,根据图中提供的信息,有下列说法:
(1)他们都行驶了18千米;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地.
其中符合图象描述的说法有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本题5个小题,每小题3分,共15分)
11.表示函数之间的关系常用 、 、 三种方法.
12.假定甲、乙两人在一次赛跑中,路程与时间的关系如图所示,那么可以知道:①甲、乙两人中先到达终点的是 ,②乙在这次赛跑中的速度为 m/s.
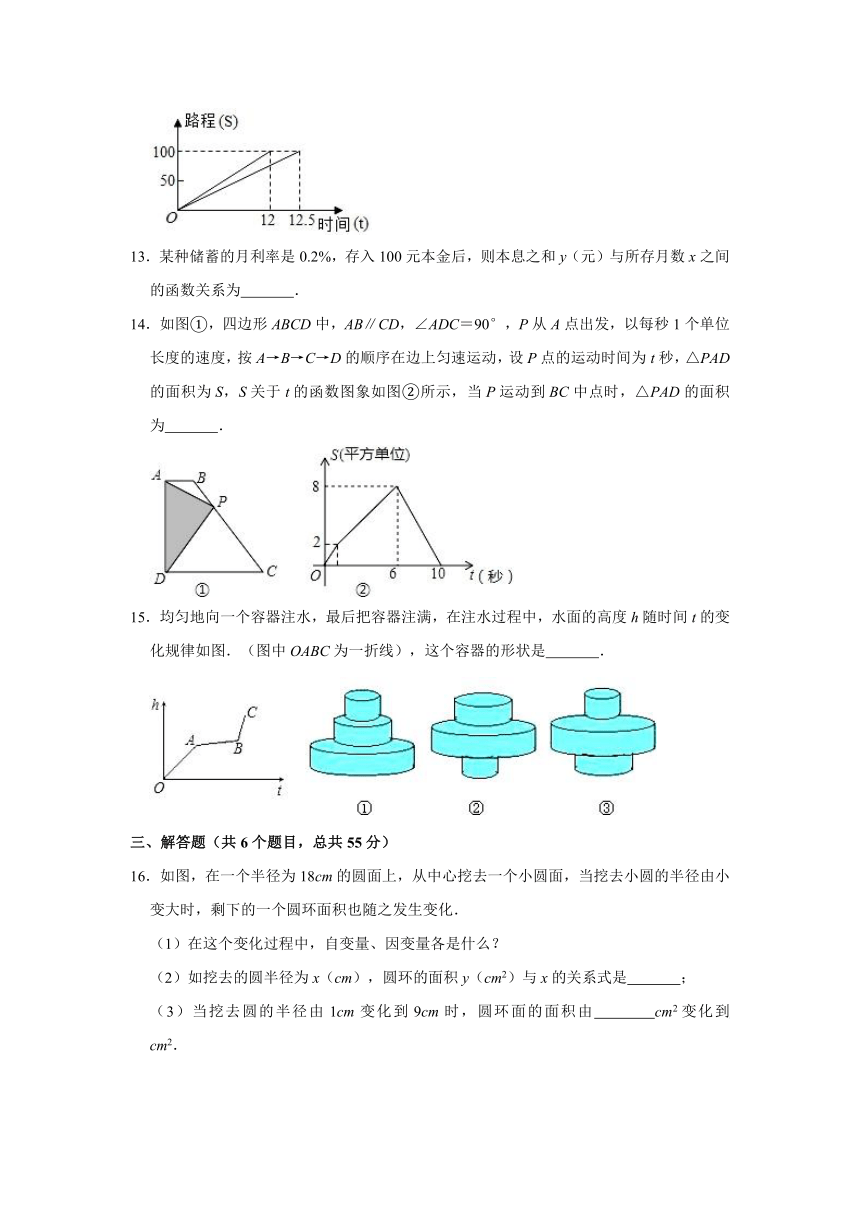
13.某种储蓄的月利率是0.2%,存入100元本金后,则本息之和y(元)与所存月数x之间的函数关系为 .
14.如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
15.均匀地向一个容器注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化规律如图.(图中OABC为一折线),这个容器的形状是 .
三、解答题(共6个题目,总共55分)
16.如图,在一个半径为18cm的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如挖去的圆半径为x(cm),圆环的面积y(cm2)与x的关系式是 ;
(3)当挖去圆的半径由1cm变化到9cm时,圆环面的面积由 cm2变化到 cm2.
17.一种豆子每千克售2元,豆子的总售价y(元)与所售豆子的质量x(千克)之间的关系如下表:
售出豆子质量x(千克) 0 0.5 1 1.5 2 2.5 3 5
总售价y(元) 0 1 2 3 4 5 6 10
(1)在这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当豆子售出5千克时,总售价是多少?
(3)按表中给出的关系,用一个式子把x与y之间的关系表示出来.
(4)当豆子售出20千克时,总售价是多少?
18.已知长方形的相邻两边的长分别是xcm和4cm,设长方形的周长为ycm.
①试写出长方形的周长y与x之间的关系式;
②求当x长为10cm,15cm时的周长;
③求当周长分别为20cm,30cm时的x值.
19.如图,在长方形ABCD中AB=12cm,AD=8cm,点P,Q都从点A出发,分别沿AB和AD运动,且保持AP=AQ,在这个变化过程中,图中的阴影部分的面积也随之变化.当AP由2cm变到8cm时,图中阴影部分的面积是增加了,还是减少了?增加或减少了多少平方厘米?
20.一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点.蚂蚁离出发点的距离S(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:
(1)请直接写出:花坛的半径是 米,a= .
(2)当t≤2时,求s与t之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回O的时间.(注:圆周率π的值取3)
21.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中 的路程与时间的关系.赛跑的全程是 米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟从出发到追上兔子用了多少分钟?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?
参考答案
一、选择题(本大题共10小题,每小题3分,共30分。在给出四个选项中,只有一项是符合题目要求的)
1.骆驼被称为“沙漠之舟”,它的体温是随时间的变化而变化的,在这一问题中,因变量是( )
A.沙漠 B.体温 C.时间 D.骆驼
解:∵骆驼的体温随时间的变化而变化,
∴自变量是时间,因变量是体温,
故选:B.
2.长方形的周长为24cm,其中一边为xcm(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=12﹣x2 C.y=(12﹣x)?x D.y=2(12﹣x)
解:∵长方形的周长为24cm,其中一边为x(其中x>0),
∴长方形的另一边长为12﹣x,
∴y=(12﹣x)?x.
故选:C.
3.地表以下的岩层温度y随着所处深度x的变化而变化,在某个地点y与x的关系可以由公式y=35x+20来表示,则y随x的增大而( )
A.增大 B.减小
C.不变 D.以上答案都不对
解:由题目分析可知:在某个地点岩层温度y随着所处深度x的变化的关系可以由公式y=35x+20来表示,由一次函数性质,进行分析,因为35>0,故应有y随x的增大而增大.
故选:A.
4.如图所示,OA、BA分别表示甲、乙两名学生运动的路程与时间的关系图象,图中S和t分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快( )
A.2.5m B.2m C.1.5m D.1m
解:观察图象知:甲跑64米用时8秒,速度为8m/s,
乙行驶52米用时8秒,速度为6.5m/s,
速度差为8﹣6.5=1.5m/s,
故选:C.
5.表格列出了一项实验的统计数据,表示皮球下落高度d与落下时弹跳高度b的关系,试问下面的哪个式子能表示这种关系(单位cm)( )
d 50 80 100 150
b 25 40 50 75
A.b=d2 B.b=2d C.b=d+25 D.b=
解:当d=150时,
A、b=d2=22500;
B、b=2d=300;
C、b=d+25=175;
D、b==75.
故选:D.
6.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x 0 1 2 3 4 5
y 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0cm
C.物体质量每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为7kg时,弹簧长度为13.5cm
解:A、y随x的增加而增加,x是自变量,y是因变量,故A选项正确;
B、弹簧不挂重物时的长度为10cm,故B选项错误;
C、物体质量每增加1kg,弹簧长度y增加0.5cm,故C选项正确;
D、由C知,y=10+0.5x,则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm,故D选项正确;
故选:B.
7.在关系式y=3x+5中,下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图象表示;⑤y与x的关系还可以用列表法和图象法表示,其中说法正确的是( )
A.①②⑤ B.①②④ C.①③⑤ D.①④⑤
解:①x是自变量,y是因变量;正确;
②x的数值可以任意选择;正确;
③y是变量,它的值与x无关;而y随x的变化而变化;错误;
④用关系式表示的不能用图象表示;错误;
⑤y与x的关系还可以用列表法和图象法表示,正确;
故选:A.
8.张大伯出去散步,从家走了20min,到了一个离家900m的阅报亭,看了10min报纸后,用了15min返回到家,如图2图象中能表示张大伯离家时间与距离之间关系的是( )
A.
B.
C.
D.
解:张大伯在行走的过程中,分三个阶段:
第一个:0到20min,距离从0变到了900m,
第二个:中间看报的时间距离没有变化,为水平线,时间为20min到30min.
第三个:后15min,即30min到45min之间,距离从900变到了0,
由此可判断是C正确,A、D的图象没有第二个阶段,而B的第二个阶段过长应是20min到30min.
故选:C.
9.为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同)一个进水管和一个出水管的进出水速度如图1所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图2所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则一定正确的论断是( )
A.①③ B.②③ C.③ D.①②③
解:①0点到1点既进水,也出水;
②1点到4点同时打开两个管进水,和一只管出水;
③4点到6点只进水,不出水.
正确的只有③.
故选:C.
10.甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离 S(千米)和行驶时间t(小时)之间的关系图象如图2所示,根据图中提供的信息,有下列说法:
(1)他们都行驶了18千米;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地.
其中符合图象描述的说法有( )
A.2个 B.3个 C.4个 D.5个
解:(1)∵两函数图象中y的最大值为18,
∴他们都行驶了18千米,说法(1)符合题意;
(2)1﹣0.5=0.5(小时),
∴甲在途中停留了0.5小时,说法(2)符合题意;
(3)观察函数图象可知,乙比甲晚出发了0.5小时,说法(3)符合题意;
(4)∵当x>1时,甲的函数图象在乙的函数图象的下方,
∴相遇后,甲的速度小于乙的速度,说法(4)符合题意;
(5)∵乙2小时到达目的地,甲2.5小时到达目的地,
∴甲比乙晚0.5小时到达目的地,说法(5)不符合题意.
综上所述:符合题意得说法有4个.
故选:C.
二、填空题(本题5个小题,每小题3分,共15分)
11.表示函数之间的关系常用 列表法 、 图象法 、 解析式法 三种方法.
解:表示函数之间的关系常常用列表法、图象法、解析式法三种方法.
12.假定甲、乙两人在一次赛跑中,路程与时间的关系如图所示,那么可以知道:①甲、乙两人中先到达终点的是 甲 ,②乙在这次赛跑中的速度为 8 m/s.
解:在通过路程相同的情况下,甲所用时间短,速度快,所以甲先到达终点;
由图象可知,甲乙两人运动的总路程相同,均为100m,
∴乙的速度:乙===8m/s.
故答案为:甲;乙的速度是8m/s.
13.某种储蓄的月利率是0.2%,存入100元本金后,则本息之和y(元)与所存月数x之间的函数关系为 y=100+0.2x .
解:∵存月数x后的利息为100×0.2%?x,
∴y=100+100×0.2%x=100+0.2x.
故填:y=100+0.2x.
14.如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 5 .
解:由图象可知,AB+BC=6,AB+BC+CD=10,
∴CD=4,
根据题意可知,当P点运动到C点时,△PAD的面积最大,S△PAD=×AD×DC=8,
∴AD=4,
又∵S△ABD=×AB×AD=2,
∴AB=1,
当P点运动到BC中点时,BP=PC,
如图,作PQ⊥AD于点Q,
∴AB∥PQ∥CD,
∴PQ为梯形ABCD的中位线,
则PQ=(AB+CD),
∴△PAD的面积=×(AB+CD)×AD=5,
故答案为:5.
15.均匀地向一个容器注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化规律如图.(图中OABC为一折线),这个容器的形状是 ③ .
解:从左面图象可以看出,OA上升较快,AB上升缓慢,BC上升最快.
从右面容器可以看出图①下面容积最大,中间容积较大,上面容积最小.
图②下面容积最小,中间容积最大,上面容积较大.
图③下面容积较大,中间容积最大,上面容积最小.
因为均匀注水,故选③.
三、解答题(共6个题目,总共55分)
16.如图,在一个半径为18cm的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如挖去的圆半径为x(cm),圆环的面积y(cm2)与x的关系式是 y=324π﹣πx2 ;
(3)当挖去圆的半径由1cm变化到9cm时,圆环面的面积由 323π cm2变化到 243π cm2.
解:(1)自变量是小圆的半径,因变量是圆环的面积;
(2)y=π×182﹣πx2=324π﹣πx2;
(3)在y=324π﹣πx2(0<x<18),当x=1时,y=323π;
当x=9时,y=243π.故圆环面的面积由323πcm2变化到243πcm2.
17.一种豆子每千克售2元,豆子的总售价y(元)与所售豆子的质量x(千克)之间的关系如下表:
售出豆子质量x(千克) 0 0.5 1 1.5 2 2.5 3 5
总售价y(元) 0 1 2 3 4 5 6 10
(1)在这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当豆子售出5千克时,总售价是多少?
(3)按表中给出的关系,用一个式子把x与y之间的关系表示出来.
(4)当豆子售出20千克时,总售价是多少?
解:(1)表格中反映的是售出豆子质量x(千克)与总售价y(元)之间的关系,售出豆子的质量x(千克)是自变量,总售价y(元)是因变量;
(2)由图表可知,
售出5千克时,总售价为10元;
(3)设x与y之间的关系为:y=kx,
把x=1,y=2代入上式,
得k=2,
x与y之间的关系为y=2x;
(4)当豆子售出20千克时,
y=2×20=40(元),
当豆子售出20千克时,总售价是40元.
18.已知长方形的相邻两边的长分别是xcm和4cm,设长方形的周长为ycm.
①试写出长方形的周长y与x之间的关系式;
②求当x长为10cm,15cm时的周长;
③求当周长分别为20cm,30cm时的x值.
解:①根据长方形的周长公式得2(x+4)=y,
∴y=2x+8;
②当x=10cm时,y=2×10+8=28cm,
当x=15时,y=2×15+8=38cm;
③当y=20cm时,2x+8=20,
解得x=6cm,
当y=30cm时,2x+8=30,
解得x=11cm.
19.如图,在长方形ABCD中AB=12cm,AD=8cm,点P,Q都从点A出发,分别沿AB和AD运动,且保持AP=AQ,在这个变化过程中,图中的阴影部分的面积也随之变化.当AP由2cm变到8cm时,图中阴影部分的面积是增加了,还是减少了?增加或减少了多少平方厘米?
解:当AP为2cm时,阴影部分的面积为:=94.
当AP为8cm时,阴影部分的面积为:=64.94﹣64=30.
所以图中阴影部分的面积减少了,减少了30平方厘米.
20.一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点.蚂蚁离出发点的距离S(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:
(1)请直接写出:花坛的半径是 4 米,a= 8 .
(2)当t≤2时,求s与t之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回O的时间.(注:圆周率π的值取3)
解:(1)由图可知,花坛的半径是4米,
蚂蚁的速度为4÷2=2米/分,
a=(4+4π)÷2=(4+4×3)÷2=8;
故答案为:4,8;
(2)设s=kt(k≠0),
∵函数图象经过点(2,4),
∴2k=4,
解得k=2,
∴s=2t;
(3)∵沿途只有一处食物,
∴蚂蚁只能在BO段吃食物,11﹣8﹣2=1,
∴蚂蚁从B爬1分钟找到食物,
4﹣1×2=2(米),
∴蚂蚁停下来吃食的地方距出发点2米,
2÷2=1(分钟),
11+1=12(分钟),
∴蚂蚁返回O的时间为12分钟.
21.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中 兔子 的路程与时间的关系,线段OD表示赛跑过程中 乌龟 的路程与时间的关系.赛跑的全程是 1500 米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟从出发到追上兔子用了多少分钟?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?
解:(1)∵乌龟是一直跑的而兔子中间有休息的时刻;
∴折线OABC表示赛跑过程中兔子的路程与时间的关系;
线段OD表示赛跑过程中乌龟的路程与时间的关系;
由图象可知:赛跑的路程为1500米;
故答案为:兔子、乌龟、1500;
(2)结合图象得出:兔子在起初每分钟跑700米.
1500÷30=50(米)
乌龟每分钟爬50米.
(3)700÷50=14(分钟)
乌龟用了14分钟追上了正在睡觉的兔子.
(4)∵48千米=48000米
∴48000÷60=800(米/分)
(1500﹣700)÷800=1(分钟)
30+0.5﹣1×2=28.5(分钟)
兔子中间停下睡觉用了28.5分钟.
一、选择题(共10小题).
1.骆驼被称为“沙漠之舟”,它的体温是随时间的变化而变化的,在这一问题中,因变量是( )
A.沙漠 B.体温 C.时间 D.骆驼
2.长方形的周长为24cm,其中一边为xcm(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=12﹣x2 C.y=(12﹣x)?x D.y=2(12﹣x)
3.地表以下的岩层温度y随着所处深度x的变化而变化,在某个地点y与x的关系可以由公式y=35x+20来表示,则y随x的增大而( )
A.增大 B.减小
C.不变 D.以上答案都不对
4.如图所示,OA、BA分别表示甲、乙两名学生运动的路程与时间的关系图象,图中S和t分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快( )
A.2.5m B.2m C.1.5m D.1m
5.表格列出了一项实验的统计数据,表示皮球下落高度d与落下时弹跳高度b的关系,试问下面的哪个式子能表示这种关系(单位cm)( )
d 50 80 100 150
b 25 40 50 75
A.b=d2 B.b=2d C.b=d+25 D.b=
6.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x 0 1 2 3 4 5
y 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0cm
C.物体质量每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为7kg时,弹簧长度为13.5cm
7.在关系式y=3x+5中,下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图象表示;⑤y与x的关系还可以用列表法和图象法表示,其中说法正确的是( )
A.①②⑤ B.①②④ C.①③⑤ D.①④⑤
8.张大伯出去散步,从家走了20min,到了一个离家900m的阅报亭,看了10min报纸后,用了15min返回到家,如图2图象中能表示张大伯离家时间与距离之间关系的是( )
A.
B.
C.
D.
9.为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同)一个进水管和一个出水管的进出水速度如图1所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图2所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则一定正确的论断是( )
A.①③ B.②③ C.③ D.①②③
10.甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离 S(千米)和行驶时间t(小时)之间的关系图象如图2所示,根据图中提供的信息,有下列说法:
(1)他们都行驶了18千米;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地.
其中符合图象描述的说法有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本题5个小题,每小题3分,共15分)
11.表示函数之间的关系常用 、 、 三种方法.
12.假定甲、乙两人在一次赛跑中,路程与时间的关系如图所示,那么可以知道:①甲、乙两人中先到达终点的是 ,②乙在这次赛跑中的速度为 m/s.
13.某种储蓄的月利率是0.2%,存入100元本金后,则本息之和y(元)与所存月数x之间的函数关系为 .
14.如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
15.均匀地向一个容器注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化规律如图.(图中OABC为一折线),这个容器的形状是 .
三、解答题(共6个题目,总共55分)
16.如图,在一个半径为18cm的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如挖去的圆半径为x(cm),圆环的面积y(cm2)与x的关系式是 ;
(3)当挖去圆的半径由1cm变化到9cm时,圆环面的面积由 cm2变化到 cm2.
17.一种豆子每千克售2元,豆子的总售价y(元)与所售豆子的质量x(千克)之间的关系如下表:
售出豆子质量x(千克) 0 0.5 1 1.5 2 2.5 3 5
总售价y(元) 0 1 2 3 4 5 6 10
(1)在这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当豆子售出5千克时,总售价是多少?
(3)按表中给出的关系,用一个式子把x与y之间的关系表示出来.
(4)当豆子售出20千克时,总售价是多少?
18.已知长方形的相邻两边的长分别是xcm和4cm,设长方形的周长为ycm.
①试写出长方形的周长y与x之间的关系式;
②求当x长为10cm,15cm时的周长;
③求当周长分别为20cm,30cm时的x值.
19.如图,在长方形ABCD中AB=12cm,AD=8cm,点P,Q都从点A出发,分别沿AB和AD运动,且保持AP=AQ,在这个变化过程中,图中的阴影部分的面积也随之变化.当AP由2cm变到8cm时,图中阴影部分的面积是增加了,还是减少了?增加或减少了多少平方厘米?
20.一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点.蚂蚁离出发点的距离S(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:
(1)请直接写出:花坛的半径是 米,a= .
(2)当t≤2时,求s与t之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回O的时间.(注:圆周率π的值取3)
21.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中 的路程与时间的关系.赛跑的全程是 米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟从出发到追上兔子用了多少分钟?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?
参考答案
一、选择题(本大题共10小题,每小题3分,共30分。在给出四个选项中,只有一项是符合题目要求的)
1.骆驼被称为“沙漠之舟”,它的体温是随时间的变化而变化的,在这一问题中,因变量是( )
A.沙漠 B.体温 C.时间 D.骆驼
解:∵骆驼的体温随时间的变化而变化,
∴自变量是时间,因变量是体温,
故选:B.
2.长方形的周长为24cm,其中一边为xcm(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=12﹣x2 C.y=(12﹣x)?x D.y=2(12﹣x)
解:∵长方形的周长为24cm,其中一边为x(其中x>0),
∴长方形的另一边长为12﹣x,
∴y=(12﹣x)?x.
故选:C.
3.地表以下的岩层温度y随着所处深度x的变化而变化,在某个地点y与x的关系可以由公式y=35x+20来表示,则y随x的增大而( )
A.增大 B.减小
C.不变 D.以上答案都不对
解:由题目分析可知:在某个地点岩层温度y随着所处深度x的变化的关系可以由公式y=35x+20来表示,由一次函数性质,进行分析,因为35>0,故应有y随x的增大而增大.
故选:A.
4.如图所示,OA、BA分别表示甲、乙两名学生运动的路程与时间的关系图象,图中S和t分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快( )
A.2.5m B.2m C.1.5m D.1m
解:观察图象知:甲跑64米用时8秒,速度为8m/s,
乙行驶52米用时8秒,速度为6.5m/s,
速度差为8﹣6.5=1.5m/s,
故选:C.
5.表格列出了一项实验的统计数据,表示皮球下落高度d与落下时弹跳高度b的关系,试问下面的哪个式子能表示这种关系(单位cm)( )
d 50 80 100 150
b 25 40 50 75
A.b=d2 B.b=2d C.b=d+25 D.b=
解:当d=150时,
A、b=d2=22500;
B、b=2d=300;
C、b=d+25=175;
D、b==75.
故选:D.
6.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x 0 1 2 3 4 5
y 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0cm
C.物体质量每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为7kg时,弹簧长度为13.5cm
解:A、y随x的增加而增加,x是自变量,y是因变量,故A选项正确;
B、弹簧不挂重物时的长度为10cm,故B选项错误;
C、物体质量每增加1kg,弹簧长度y增加0.5cm,故C选项正确;
D、由C知,y=10+0.5x,则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm,故D选项正确;
故选:B.
7.在关系式y=3x+5中,下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图象表示;⑤y与x的关系还可以用列表法和图象法表示,其中说法正确的是( )
A.①②⑤ B.①②④ C.①③⑤ D.①④⑤
解:①x是自变量,y是因变量;正确;
②x的数值可以任意选择;正确;
③y是变量,它的值与x无关;而y随x的变化而变化;错误;
④用关系式表示的不能用图象表示;错误;
⑤y与x的关系还可以用列表法和图象法表示,正确;
故选:A.
8.张大伯出去散步,从家走了20min,到了一个离家900m的阅报亭,看了10min报纸后,用了15min返回到家,如图2图象中能表示张大伯离家时间与距离之间关系的是( )
A.
B.
C.
D.
解:张大伯在行走的过程中,分三个阶段:
第一个:0到20min,距离从0变到了900m,
第二个:中间看报的时间距离没有变化,为水平线,时间为20min到30min.
第三个:后15min,即30min到45min之间,距离从900变到了0,
由此可判断是C正确,A、D的图象没有第二个阶段,而B的第二个阶段过长应是20min到30min.
故选:C.
9.为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同)一个进水管和一个出水管的进出水速度如图1所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图2所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则一定正确的论断是( )
A.①③ B.②③ C.③ D.①②③
解:①0点到1点既进水,也出水;
②1点到4点同时打开两个管进水,和一只管出水;
③4点到6点只进水,不出水.
正确的只有③.
故选:C.
10.甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离 S(千米)和行驶时间t(小时)之间的关系图象如图2所示,根据图中提供的信息,有下列说法:
(1)他们都行驶了18千米;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地.
其中符合图象描述的说法有( )
A.2个 B.3个 C.4个 D.5个
解:(1)∵两函数图象中y的最大值为18,
∴他们都行驶了18千米,说法(1)符合题意;
(2)1﹣0.5=0.5(小时),
∴甲在途中停留了0.5小时,说法(2)符合题意;
(3)观察函数图象可知,乙比甲晚出发了0.5小时,说法(3)符合题意;
(4)∵当x>1时,甲的函数图象在乙的函数图象的下方,
∴相遇后,甲的速度小于乙的速度,说法(4)符合题意;
(5)∵乙2小时到达目的地,甲2.5小时到达目的地,
∴甲比乙晚0.5小时到达目的地,说法(5)不符合题意.
综上所述:符合题意得说法有4个.
故选:C.
二、填空题(本题5个小题,每小题3分,共15分)
11.表示函数之间的关系常用 列表法 、 图象法 、 解析式法 三种方法.
解:表示函数之间的关系常常用列表法、图象法、解析式法三种方法.
12.假定甲、乙两人在一次赛跑中,路程与时间的关系如图所示,那么可以知道:①甲、乙两人中先到达终点的是 甲 ,②乙在这次赛跑中的速度为 8 m/s.
解:在通过路程相同的情况下,甲所用时间短,速度快,所以甲先到达终点;
由图象可知,甲乙两人运动的总路程相同,均为100m,
∴乙的速度:乙===8m/s.
故答案为:甲;乙的速度是8m/s.
13.某种储蓄的月利率是0.2%,存入100元本金后,则本息之和y(元)与所存月数x之间的函数关系为 y=100+0.2x .
解:∵存月数x后的利息为100×0.2%?x,
∴y=100+100×0.2%x=100+0.2x.
故填:y=100+0.2x.
14.如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 5 .
解:由图象可知,AB+BC=6,AB+BC+CD=10,
∴CD=4,
根据题意可知,当P点运动到C点时,△PAD的面积最大,S△PAD=×AD×DC=8,
∴AD=4,
又∵S△ABD=×AB×AD=2,
∴AB=1,
当P点运动到BC中点时,BP=PC,
如图,作PQ⊥AD于点Q,
∴AB∥PQ∥CD,
∴PQ为梯形ABCD的中位线,
则PQ=(AB+CD),
∴△PAD的面积=×(AB+CD)×AD=5,
故答案为:5.
15.均匀地向一个容器注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化规律如图.(图中OABC为一折线),这个容器的形状是 ③ .
解:从左面图象可以看出,OA上升较快,AB上升缓慢,BC上升最快.
从右面容器可以看出图①下面容积最大,中间容积较大,上面容积最小.
图②下面容积最小,中间容积最大,上面容积较大.
图③下面容积较大,中间容积最大,上面容积最小.
因为均匀注水,故选③.
三、解答题(共6个题目,总共55分)
16.如图,在一个半径为18cm的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如挖去的圆半径为x(cm),圆环的面积y(cm2)与x的关系式是 y=324π﹣πx2 ;
(3)当挖去圆的半径由1cm变化到9cm时,圆环面的面积由 323π cm2变化到 243π cm2.
解:(1)自变量是小圆的半径,因变量是圆环的面积;
(2)y=π×182﹣πx2=324π﹣πx2;
(3)在y=324π﹣πx2(0<x<18),当x=1时,y=323π;
当x=9时,y=243π.故圆环面的面积由323πcm2变化到243πcm2.
17.一种豆子每千克售2元,豆子的总售价y(元)与所售豆子的质量x(千克)之间的关系如下表:
售出豆子质量x(千克) 0 0.5 1 1.5 2 2.5 3 5
总售价y(元) 0 1 2 3 4 5 6 10
(1)在这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当豆子售出5千克时,总售价是多少?
(3)按表中给出的关系,用一个式子把x与y之间的关系表示出来.
(4)当豆子售出20千克时,总售价是多少?
解:(1)表格中反映的是售出豆子质量x(千克)与总售价y(元)之间的关系,售出豆子的质量x(千克)是自变量,总售价y(元)是因变量;
(2)由图表可知,
售出5千克时,总售价为10元;
(3)设x与y之间的关系为:y=kx,
把x=1,y=2代入上式,
得k=2,
x与y之间的关系为y=2x;
(4)当豆子售出20千克时,
y=2×20=40(元),
当豆子售出20千克时,总售价是40元.
18.已知长方形的相邻两边的长分别是xcm和4cm,设长方形的周长为ycm.
①试写出长方形的周长y与x之间的关系式;
②求当x长为10cm,15cm时的周长;
③求当周长分别为20cm,30cm时的x值.
解:①根据长方形的周长公式得2(x+4)=y,
∴y=2x+8;
②当x=10cm时,y=2×10+8=28cm,
当x=15时,y=2×15+8=38cm;
③当y=20cm时,2x+8=20,
解得x=6cm,
当y=30cm时,2x+8=30,
解得x=11cm.
19.如图,在长方形ABCD中AB=12cm,AD=8cm,点P,Q都从点A出发,分别沿AB和AD运动,且保持AP=AQ,在这个变化过程中,图中的阴影部分的面积也随之变化.当AP由2cm变到8cm时,图中阴影部分的面积是增加了,还是减少了?增加或减少了多少平方厘米?
解:当AP为2cm时,阴影部分的面积为:=94.
当AP为8cm时,阴影部分的面积为:=64.94﹣64=30.
所以图中阴影部分的面积减少了,减少了30平方厘米.
20.一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点.蚂蚁离出发点的距离S(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:
(1)请直接写出:花坛的半径是 4 米,a= 8 .
(2)当t≤2时,求s与t之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回O的时间.(注:圆周率π的值取3)
解:(1)由图可知,花坛的半径是4米,
蚂蚁的速度为4÷2=2米/分,
a=(4+4π)÷2=(4+4×3)÷2=8;
故答案为:4,8;
(2)设s=kt(k≠0),
∵函数图象经过点(2,4),
∴2k=4,
解得k=2,
∴s=2t;
(3)∵沿途只有一处食物,
∴蚂蚁只能在BO段吃食物,11﹣8﹣2=1,
∴蚂蚁从B爬1分钟找到食物,
4﹣1×2=2(米),
∴蚂蚁停下来吃食的地方距出发点2米,
2÷2=1(分钟),
11+1=12(分钟),
∴蚂蚁返回O的时间为12分钟.
21.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中 兔子 的路程与时间的关系,线段OD表示赛跑过程中 乌龟 的路程与时间的关系.赛跑的全程是 1500 米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟从出发到追上兔子用了多少分钟?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?
解:(1)∵乌龟是一直跑的而兔子中间有休息的时刻;
∴折线OABC表示赛跑过程中兔子的路程与时间的关系;
线段OD表示赛跑过程中乌龟的路程与时间的关系;
由图象可知:赛跑的路程为1500米;
故答案为:兔子、乌龟、1500;
(2)结合图象得出:兔子在起初每分钟跑700米.
1500÷30=50(米)
乌龟每分钟爬50米.
(3)700÷50=14(分钟)
乌龟用了14分钟追上了正在睡觉的兔子.
(4)∵48千米=48000米
∴48000÷60=800(米/分)
(1500﹣700)÷800=1(分钟)
30+0.5﹣1×2=28.5(分钟)
兔子中间停下睡觉用了28.5分钟.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
