18.2.1.1矩形的性质课件(20张)
图片预览



文档简介
(共20张PPT)
人教版数学教材八年级下
18.2特殊的平行四边形
矩形(1)
D
B
A
C
O
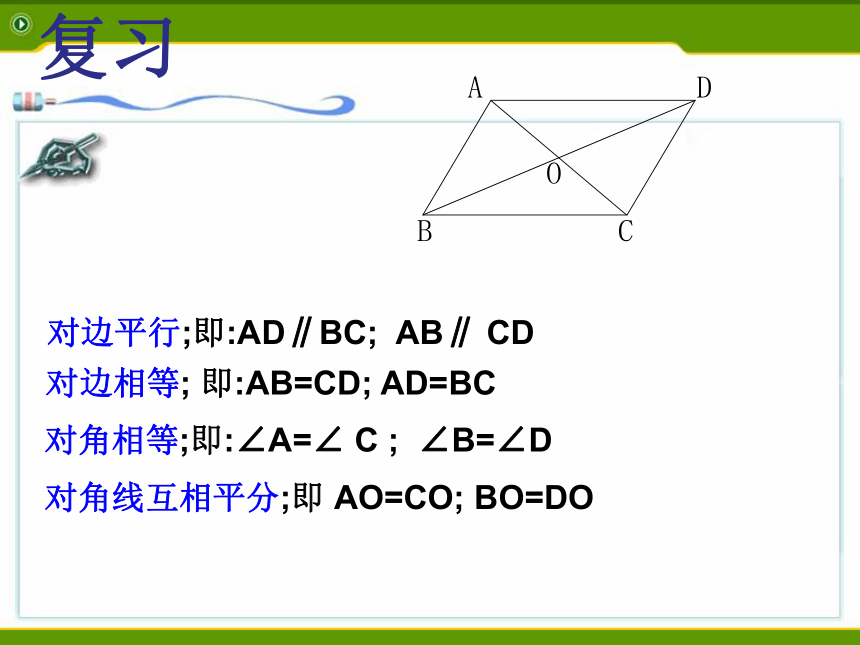
对边平行;即:AD∥BC;
AB∥
CD
对边相等;
即:AB=CD;
AD=BC
对角相等;即:∠A=∠
C
;
∠B=∠D
对角线互相平分;即
AO=CO;
BO=DO
复习
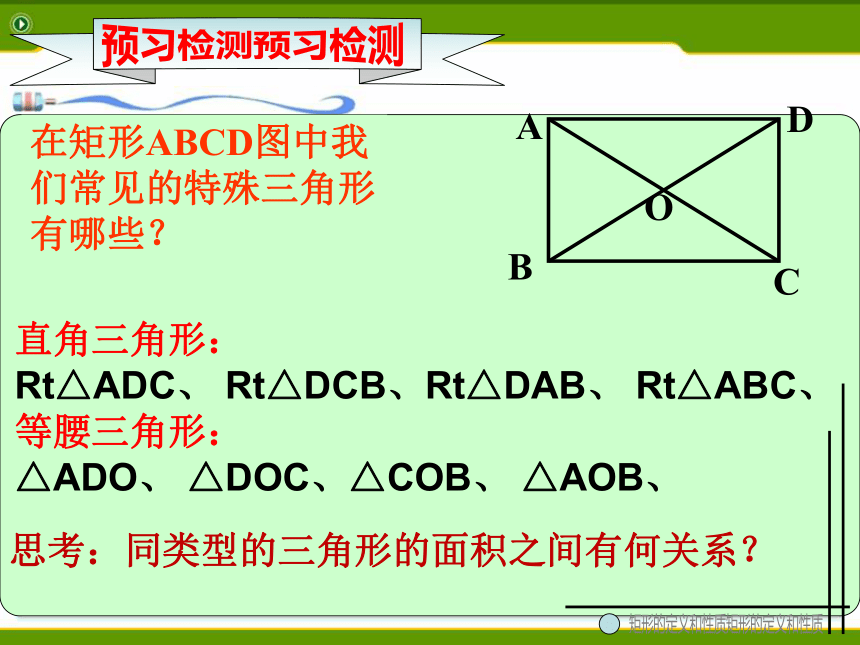
直角三角形:
Rt△ADC、
Rt△DCB、Rt△DAB、
Rt△ABC、
等腰三角形:
△ADO、
△DOC、△COB、
△AOB、
预习检测
矩形的定义和性质
在矩形ABCD图中我们常见的特殊三角形有哪些?
B
O
D
C
A
思考:同类型的三角形的面积之间有何关系?
八年级
数学
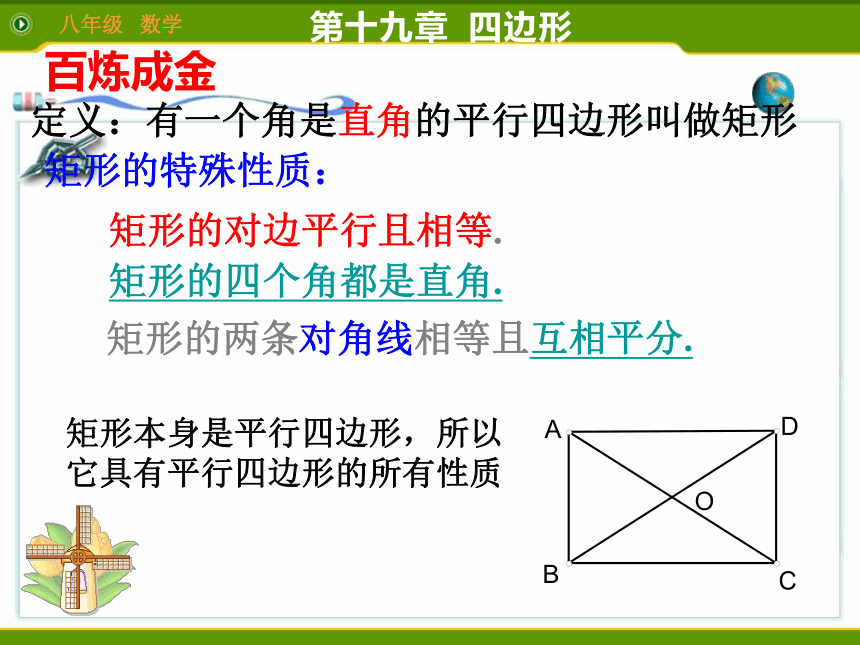
百炼成金
第十九章
四边形
矩形的特殊性质:
矩形的四个角都是直角.
矩形的两条对角线相等
且互相平分.
矩形的对边平行且相等.
矩形本身是平行四边形,所以它具有平行四边形的所有性质
定义:有一个角是直角的平行四边形叫做矩形
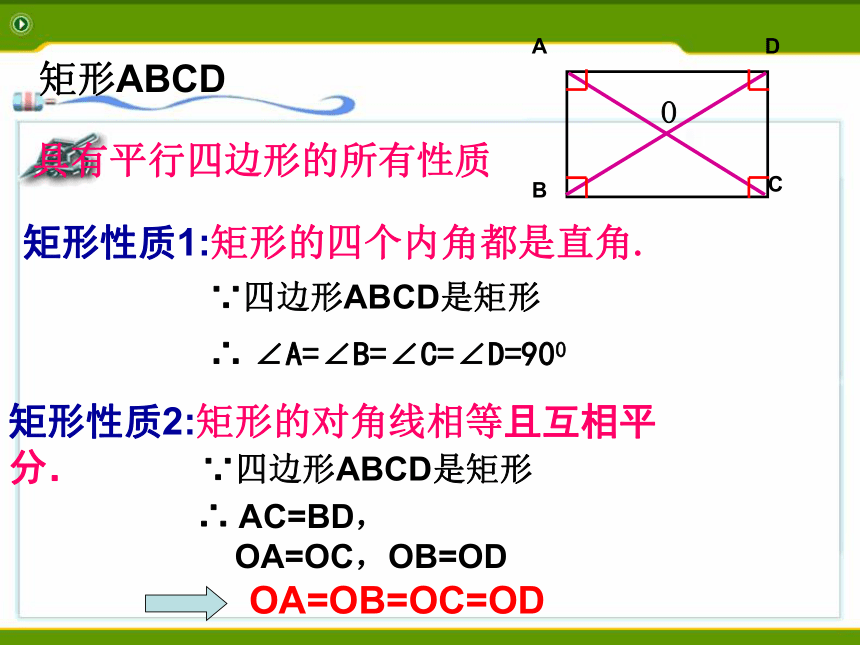
矩形性质1:矩形的四个内角都是直角.
矩形性质2:矩形的对角线相等且互相平分.
A
B
C
D
∵四边形ABCD是矩形
矩形ABCD
∴
AC=BD,
OA=OC,OB=OD
具有平行四边形的所有性质
O
∵四边形ABCD是矩形
∴
∠A=∠B=∠C=∠D=900
OA=OB=OC=OD
A
B
C
D
O
探索矩形的对称性:
矩形是中心对称图形,又是轴对称图形
想一想
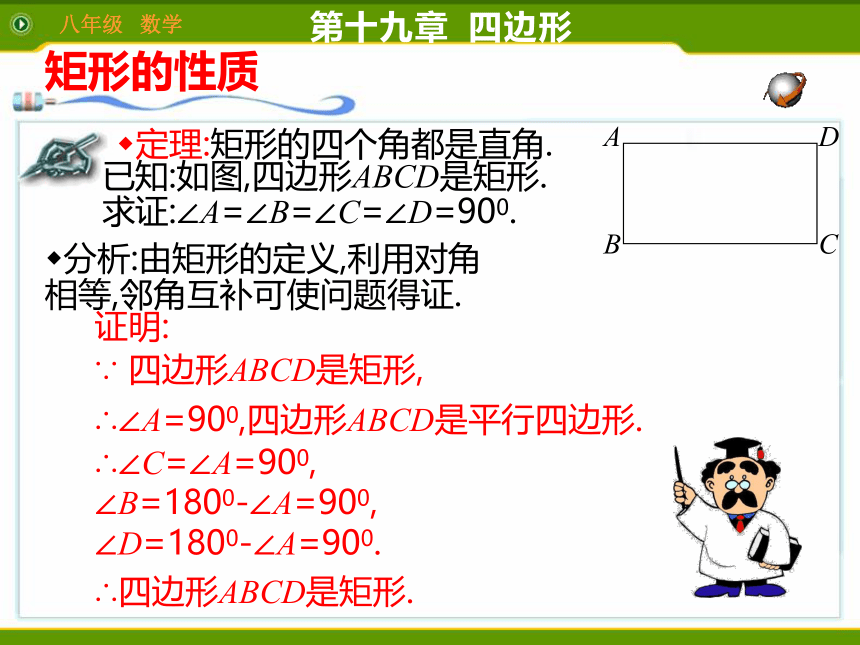
定理:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形.
分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.
证明:
∵
四边形ABCD是矩形,
∴∠A=900,四边形ABCD是平行四边形.
∴∠C=∠A=900,
∠B=1800-∠A=900,
∠D=1800-∠A=900.
求证:∠A=∠B=∠C=∠D=900.
∴四边形ABCD是矩形.
D
B
C
A
八年级
数学
矩形的性质
第十九章
四边形
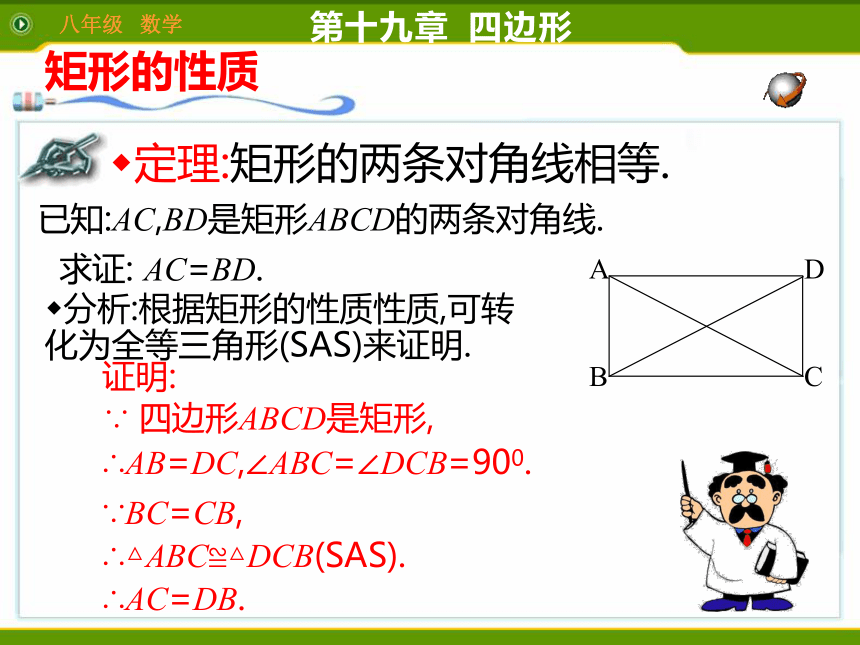
定理:矩形的两条对角线相等.
已知:AC,BD是矩形ABCD的两条对角线.
求证:
AC=BD.
证明:
∵
四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=900.
分析:根据矩形的性质性质,可转化为全等三角形(SAS)来证明.
D
B
C
A
∵BC=CB,
∴△ABC≌△DCB(SAS).
∴AC=DB.
八年级
数学
矩形的性质
第十九章
四边形
设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段?
它与AC有什么大小关系?为什么?
D
B
C
A
E
由此可得推论:
直角三角形斜边上的中线等于斜边的一半
BE是Rt△ABC中斜边AC上的中线.
BE等于AC的一半.
∵
AC=BD,BE=DE,
议一议:
八年级
数学
第十九章
四边形
矩形的定义及性质
一个角是直角
定义:有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
性质定理1
矩形的四个角都是直角
性质定理2
矩形的对角线相等★
矩形性质
角
边
对角线
对称性
推论:直角三角形斜边上的中线等于斜边的一半★
例1
练习
小结
四个角都
是直角
对边平行
且相等
互相平分
且相等
是轴对称
图形
生活中的数学
给你一根足够长的绳子,你能检查教室的门窗或你的桌子是不是矩形吗?你怎样检查?解释其中的道理。
八年级
数学
学以致用
第十九章
四边形
问题:
体育节中有一投圈游戏,四个同学分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OB=OD
=
OA=OC
生活链接---投圈游戏
学以致用
矩形的定义和性质
1.
矩形具有而一般平行四边形不具有的性质是(
).
A、对角线相等
B、对边相等
C、对角相等
D、对角线互相平分
2、
矩形的一组邻边长分别是3cm和4cm,
则它的对角线长是
cm.
A
5
3、下列性质中,矩形不一定具有的是(
)
A.对角线相等
B.
四个角都相等
C.是轴对称图形
D.对角线垂直
D
4、如图,已知ABCD为矩形,若沿AE折叠,使D点落在BC边上F点处,如果∠BAF=600,那么∠DAE等于(
)
A.150
B.300
C.450
D.600
A
F
E
D
C
B
A
学以致用
D
C
B
A
┓
5.
已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.
(1)若BD=3㎝,则AC=______
㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.
6
5
10
学以致用
6.设矩形ABCD和矩形AEFC的面积分别为S1、S2,则二者的大小关系是:S1________S2.
学以致用
A
7.在
中,斜边AC上的中线
和高分别是6cm和5cm,则
的
面积S=(
)。
A
B
C
D
E
30cm2
学以致用
8、已知:如图,AC,BD是矩形ABCD的两条对线,AC,BD相交于点O,∠AOD=1200,AB=2.5cm.
求矩形对角线的长.
解:
∵四边形ABCD是矩形,
∴BD=2AB=2×2.5=5(cm).
∴AC=BD,且
∵∠DAB=900,
∵∠AOD=1200,
D
B
C
A
O
∴∠ODA=∠OAD=
学以致用
9、已知:如图,过矩形ABCD的顶点作CE//BD,交AB的延长线于E。
求证:∠CAE=∠CEA
A
B
C
D
E
O
学以致用
在矩形ABCD中,对角线AC与BD相交于点O,已知AB=6,BC=8,
(1)求AC=----,OA=OD=----,
(2)矩形ABCD的周长是------,面积是-----。
10
5
28
48
A
B
C
D
O
6
8
(3)
S
△OAD=
。
12
(4)P点是AD上任意一点,
且PE?AC,PF?BD,垂足各为E,F
求PE+PF=
。
·
P
4.8
E
F
(5)过点O作OG
?
AC交AD于点G,则AG=
.
G
6.25或25/4
拓展延伸
人教版数学教材八年级下
18.2特殊的平行四边形
矩形(1)
D
B
A
C
O
对边平行;即:AD∥BC;
AB∥
CD
对边相等;
即:AB=CD;
AD=BC
对角相等;即:∠A=∠
C
;
∠B=∠D
对角线互相平分;即
AO=CO;
BO=DO
复习
直角三角形:
Rt△ADC、
Rt△DCB、Rt△DAB、
Rt△ABC、
等腰三角形:
△ADO、
△DOC、△COB、
△AOB、
预习检测
矩形的定义和性质
在矩形ABCD图中我们常见的特殊三角形有哪些?
B
O
D
C
A
思考:同类型的三角形的面积之间有何关系?
八年级
数学
百炼成金
第十九章
四边形
矩形的特殊性质:
矩形的四个角都是直角.
矩形的两条对角线相等
且互相平分.
矩形的对边平行且相等.
矩形本身是平行四边形,所以它具有平行四边形的所有性质
定义:有一个角是直角的平行四边形叫做矩形
矩形性质1:矩形的四个内角都是直角.
矩形性质2:矩形的对角线相等且互相平分.
A
B
C
D
∵四边形ABCD是矩形
矩形ABCD
∴
AC=BD,
OA=OC,OB=OD
具有平行四边形的所有性质
O
∵四边形ABCD是矩形
∴
∠A=∠B=∠C=∠D=900
OA=OB=OC=OD
A
B
C
D
O
探索矩形的对称性:
矩形是中心对称图形,又是轴对称图形
想一想
定理:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形.
分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.
证明:
∵
四边形ABCD是矩形,
∴∠A=900,四边形ABCD是平行四边形.
∴∠C=∠A=900,
∠B=1800-∠A=900,
∠D=1800-∠A=900.
求证:∠A=∠B=∠C=∠D=900.
∴四边形ABCD是矩形.
D
B
C
A
八年级
数学
矩形的性质
第十九章
四边形
定理:矩形的两条对角线相等.
已知:AC,BD是矩形ABCD的两条对角线.
求证:
AC=BD.
证明:
∵
四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=900.
分析:根据矩形的性质性质,可转化为全等三角形(SAS)来证明.
D
B
C
A
∵BC=CB,
∴△ABC≌△DCB(SAS).
∴AC=DB.
八年级
数学
矩形的性质
第十九章
四边形
设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段?
它与AC有什么大小关系?为什么?
D
B
C
A
E
由此可得推论:
直角三角形斜边上的中线等于斜边的一半
BE是Rt△ABC中斜边AC上的中线.
BE等于AC的一半.
∵
AC=BD,BE=DE,
议一议:
八年级
数学
第十九章
四边形
矩形的定义及性质
一个角是直角
定义:有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
性质定理1
矩形的四个角都是直角
性质定理2
矩形的对角线相等★
矩形性质
角
边
对角线
对称性
推论:直角三角形斜边上的中线等于斜边的一半★
例1
练习
小结
四个角都
是直角
对边平行
且相等
互相平分
且相等
是轴对称
图形
生活中的数学
给你一根足够长的绳子,你能检查教室的门窗或你的桌子是不是矩形吗?你怎样检查?解释其中的道理。
八年级
数学
学以致用
第十九章
四边形
问题:
体育节中有一投圈游戏,四个同学分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OB=OD
=
OA=OC
生活链接---投圈游戏
学以致用
矩形的定义和性质
1.
矩形具有而一般平行四边形不具有的性质是(
).
A、对角线相等
B、对边相等
C、对角相等
D、对角线互相平分
2、
矩形的一组邻边长分别是3cm和4cm,
则它的对角线长是
cm.
A
5
3、下列性质中,矩形不一定具有的是(
)
A.对角线相等
B.
四个角都相等
C.是轴对称图形
D.对角线垂直
D
4、如图,已知ABCD为矩形,若沿AE折叠,使D点落在BC边上F点处,如果∠BAF=600,那么∠DAE等于(
)
A.150
B.300
C.450
D.600
A
F
E
D
C
B
A
学以致用
D
C
B
A
┓
5.
已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.
(1)若BD=3㎝,则AC=______
㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.
6
5
10
学以致用
6.设矩形ABCD和矩形AEFC的面积分别为S1、S2,则二者的大小关系是:S1________S2.
学以致用
A
7.在
中,斜边AC上的中线
和高分别是6cm和5cm,则
的
面积S=(
)。
A
B
C
D
E
30cm2
学以致用
8、已知:如图,AC,BD是矩形ABCD的两条对线,AC,BD相交于点O,∠AOD=1200,AB=2.5cm.
求矩形对角线的长.
解:
∵四边形ABCD是矩形,
∴BD=2AB=2×2.5=5(cm).
∴AC=BD,且
∵∠DAB=900,
∵∠AOD=1200,
D
B
C
A
O
∴∠ODA=∠OAD=
学以致用
9、已知:如图,过矩形ABCD的顶点作CE//BD,交AB的延长线于E。
求证:∠CAE=∠CEA
A
B
C
D
E
O
学以致用
在矩形ABCD中,对角线AC与BD相交于点O,已知AB=6,BC=8,
(1)求AC=----,OA=OD=----,
(2)矩形ABCD的周长是------,面积是-----。
10
5
28
48
A
B
C
D
O
6
8
(3)
S
△OAD=
。
12
(4)P点是AD上任意一点,
且PE?AC,PF?BD,垂足各为E,F
求PE+PF=
。
·
P
4.8
E
F
(5)过点O作OG
?
AC交AD于点G,则AG=
.
G
6.25或25/4
拓展延伸
