四年级下册数学课件-4.1.3 三角形的内角和冀教版(共22张PPT)
文档属性
| 名称 | 四年级下册数学课件-4.1.3 三角形的内角和冀教版(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-31 21:12:52 | ||
图片预览





文档简介
(共22张PPT)
三角形的内角和
形状似座山,稳定性能坚。
三竿首尾连,学问不简单。
(打一图形名称)
三角形
你知道它们是什么三角形吗?第3个图形中被遮住的两个角是什么角?会是两个直角吗?为什么?
1
3
2
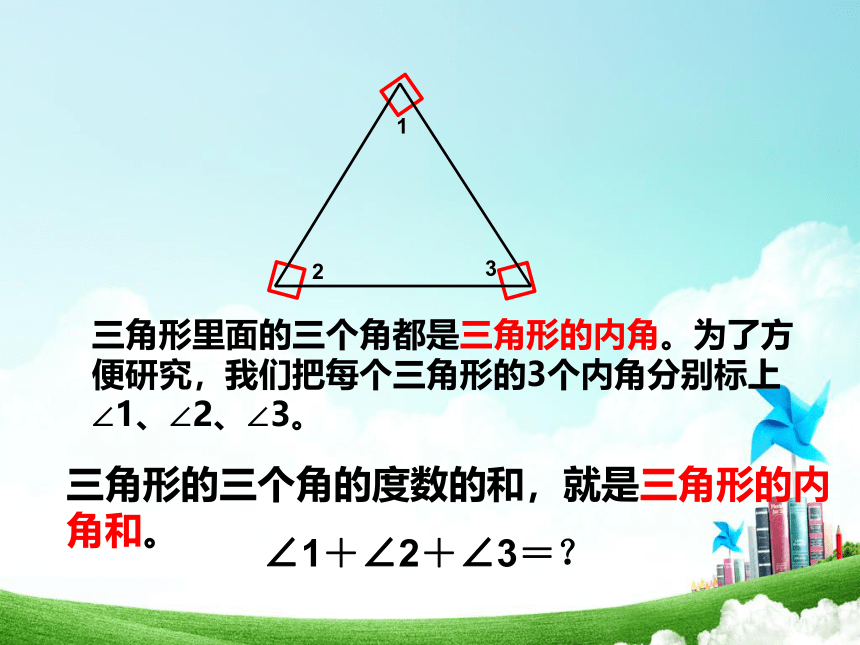
三角形里面的三个角都是三角形的内角。为了方便研究,我们把每个三角形的3个内角分别标上∠1、∠2、∠3。
三角形的三个角的度数的和,就是三角形的内角和。
∠1+∠2+∠3=?
你用什么方法来验证这个猜想?
三角形的三个内角和是多少度?
猜一猜:
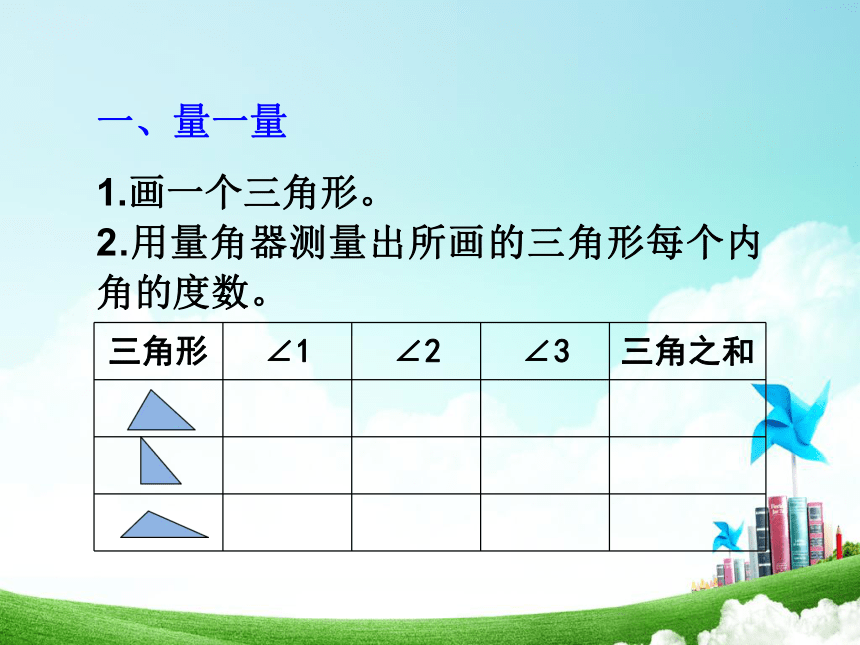
1.画一个三角形。
2.用量角器测量出所画的三角形每个内角的度数。
一、量一量
三角形
∠1
∠2
∠3
三角之和
通过量一量、算一算,我们发现:三角形的内角和可能是180°。
还有什么方法能够进一步验证吗?
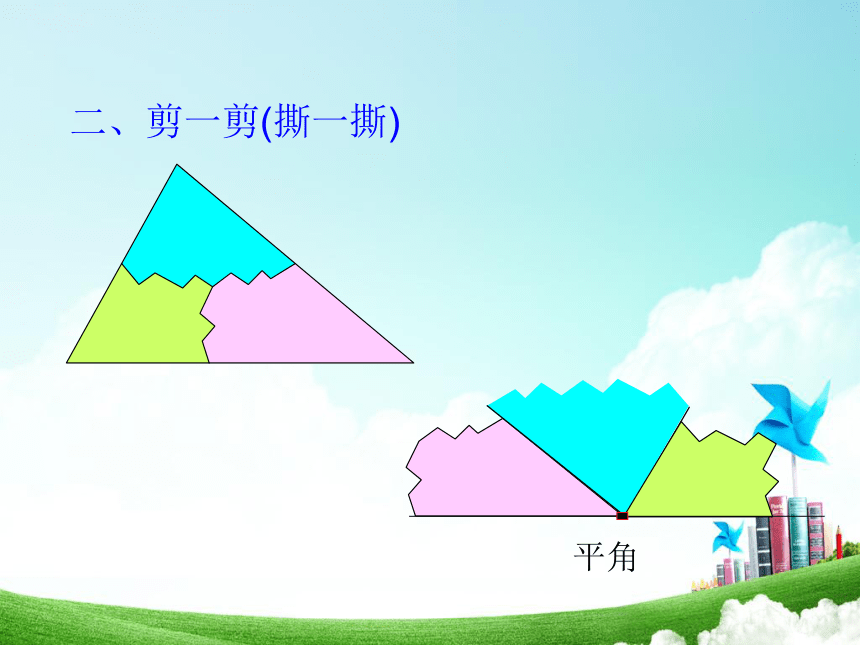
平角
二、剪一剪(撕一撕)
1
中点
中点
中点
中点
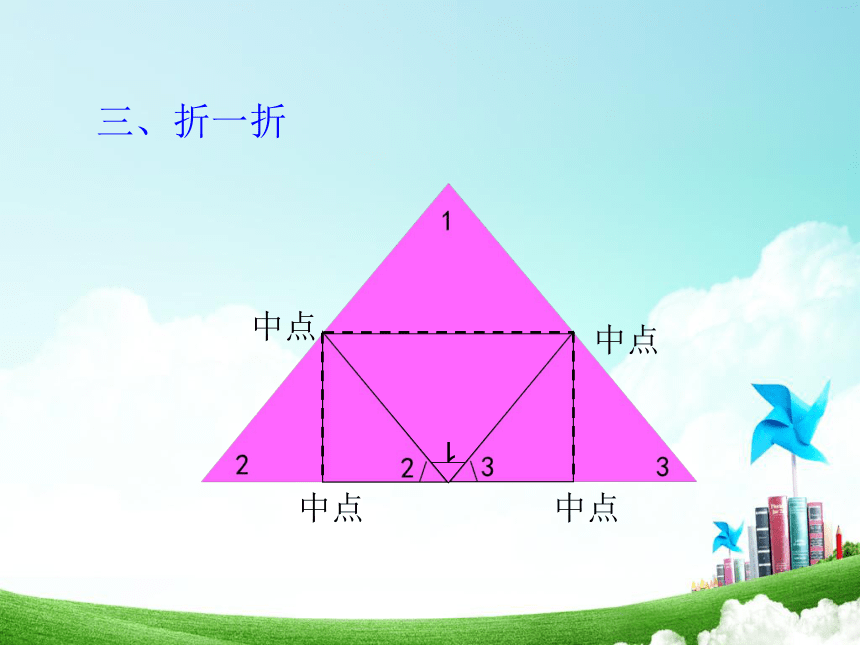
三、折一折
三角形的内角和是180°。
∠1+∠2+∠3=180°
任意直角三角形的内角和是180
°。
长方形的四个角都是直角,所以长方形的内角和
应为:90°×4=360°。将长方形沿对角线分割,
可以分成两个完全相等的三角形,所以直角三角形
内角和应为:360°÷2=180°。
操作总会有误差,有没
有别的办法说明呢?
1
4
任意三角形的内角和是180
°。
沿高可以将任意三角形分成两个直角三角形。
由于前面证明了任意直角三角形的内角和是180°,
因此两个直角三角形的内角和应为:180°×2=360°。
而直角三角形的两个直角不属于分割前三角形的内角,
因此任意三角形的内角和应为:360°-180°=180°。
1
2
3
4
2
3
操作总会有误差,有没有别的办法说明呢?
法国著名数学家帕斯卡,在12岁时就已经发现了这种用直角三角形的内角和来证明其他三角形内角和是180
°的方法。
(2)
60°,70°,90°
(3)
30°,40°,50°
(4)
50°,50°,80°
(5)
60°,60°,60°
(1)
80°,95°,5°
1.(口答)下列各组角是同一个三角形的内角吗?为什么?
2.根据三角形的内角和,可以求出未知角的度数。
①已知两个角的度数,求未知角的度数。
下图中,∠1=140°,∠3=25°。求∠2的度数。
180°-140°-25°=15°
我是直角三角形,一个锐角是40°。
我是等腰三角形,顶角是96°。
②
如果只告诉一个角的度数,你会求其它角的度数吗?
③如果三个角的度数都不告诉你呢?
等边三角形的每个内角都是60°。
3.变化中强化结论
在一个三角形中可能会出现2个直角吗?
在一个三角形中可能会出现2个钝角吗?
请你用今天学习的知识进行解释。
4.应用解释。
更多互动练习见“课堂训练”下的随堂小测、达标检测等,助您大数据分析!
探究方法:1.量算(有误差)
2.剪拼
3.折拼
三角形的内角和
结论:三角形的内角和是180度。
本节课你都有哪些收获?
三角形的内角和
形状似座山,稳定性能坚。
三竿首尾连,学问不简单。
(打一图形名称)
三角形
你知道它们是什么三角形吗?第3个图形中被遮住的两个角是什么角?会是两个直角吗?为什么?
1
3
2
三角形里面的三个角都是三角形的内角。为了方便研究,我们把每个三角形的3个内角分别标上∠1、∠2、∠3。
三角形的三个角的度数的和,就是三角形的内角和。
∠1+∠2+∠3=?
你用什么方法来验证这个猜想?
三角形的三个内角和是多少度?
猜一猜:
1.画一个三角形。
2.用量角器测量出所画的三角形每个内角的度数。
一、量一量
三角形
∠1
∠2
∠3
三角之和
通过量一量、算一算,我们发现:三角形的内角和可能是180°。
还有什么方法能够进一步验证吗?
平角
二、剪一剪(撕一撕)
1
中点
中点
中点
中点
三、折一折
三角形的内角和是180°。
∠1+∠2+∠3=180°
任意直角三角形的内角和是180
°。
长方形的四个角都是直角,所以长方形的内角和
应为:90°×4=360°。将长方形沿对角线分割,
可以分成两个完全相等的三角形,所以直角三角形
内角和应为:360°÷2=180°。
操作总会有误差,有没
有别的办法说明呢?
1
4
任意三角形的内角和是180
°。
沿高可以将任意三角形分成两个直角三角形。
由于前面证明了任意直角三角形的内角和是180°,
因此两个直角三角形的内角和应为:180°×2=360°。
而直角三角形的两个直角不属于分割前三角形的内角,
因此任意三角形的内角和应为:360°-180°=180°。
1
2
3
4
2
3
操作总会有误差,有没有别的办法说明呢?
法国著名数学家帕斯卡,在12岁时就已经发现了这种用直角三角形的内角和来证明其他三角形内角和是180
°的方法。
(2)
60°,70°,90°
(3)
30°,40°,50°
(4)
50°,50°,80°
(5)
60°,60°,60°
(1)
80°,95°,5°
1.(口答)下列各组角是同一个三角形的内角吗?为什么?
2.根据三角形的内角和,可以求出未知角的度数。
①已知两个角的度数,求未知角的度数。
下图中,∠1=140°,∠3=25°。求∠2的度数。
180°-140°-25°=15°
我是直角三角形,一个锐角是40°。
我是等腰三角形,顶角是96°。
②
如果只告诉一个角的度数,你会求其它角的度数吗?
③如果三个角的度数都不告诉你呢?
等边三角形的每个内角都是60°。
3.变化中强化结论
在一个三角形中可能会出现2个直角吗?
在一个三角形中可能会出现2个钝角吗?
请你用今天学习的知识进行解释。
4.应用解释。
更多互动练习见“课堂训练”下的随堂小测、达标检测等,助您大数据分析!
探究方法:1.量算(有误差)
2.剪拼
3.折拼
三角形的内角和
结论:三角形的内角和是180度。
本节课你都有哪些收获?
