2020-2021学年北师大版八年级数学下册3.1.2图形的平移(二) 同步练习题(Word版,附答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册3.1.2图形的平移(二) 同步练习题(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 198.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 09:33:46 | ||
图片预览


文档简介
2020-2021学年北师大版八年级数学下册第三章
3.1.2图形的平移(二)
同步练习题
A组(基础题)
一、填空题
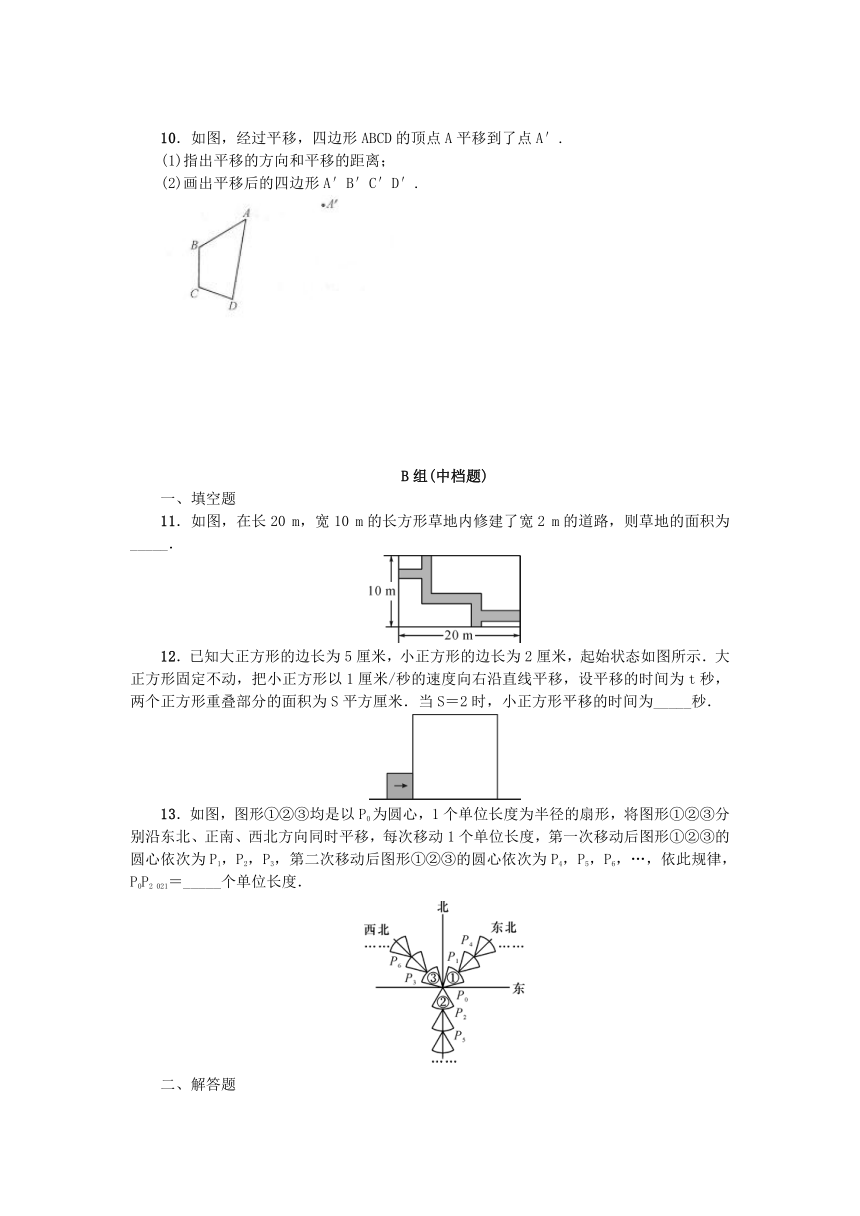
1.如图,将直线l1沿AB的方向平移得到l2.若∠1=40°,则∠2=_____.
2.如图,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,则在“笑脸”图标中的点P的对应点的坐标是_____.
3.(1)如图,左边的图形是由右边的图形向_____平移_____个单位长度得到的;
(2)将点P(-4,y)先向左平移2个单位长度,再向下平移3个单位长度后得到点Q(x,-1),则x=_____,y=_____.
4.(1)利用平移的知识计算,所给图形的周长为_____;
(2)如图,△ABC的顶点都在网格点上,将△ABC向右平移3个单位长度,再向上平移2个单位长度,则平移后得到的△A′B′C′的顶点A′的坐标是_____.
二、选择题
5.下列说法正确的是(
)
A.平移改变图形的形状
B.平移改变图形的大小
C.平移改变图形的形状和大小
D.平移不改变图形的形状和大小
6.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都加上3,则所得图形与原图形的关系是:将原图形(
)
A.向左平移3个单位长度
B.向右平移3个单位长度
C.向上平移3个单位长度
D.向下平移3个单位长度
7.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是(
)
A.(1,0)
B.(,)
C.(1,)
D.(-1,)
8.下列图形中,分别把△ABC平移后能得到△DEF的是(
)
三、解答题
9.如图,方格是由边长为1个单位长度的正方形组成的.
(1)求图中阴影部分的面积;
(2)画出△ABC向右平移2个单位长度后得到的图形.
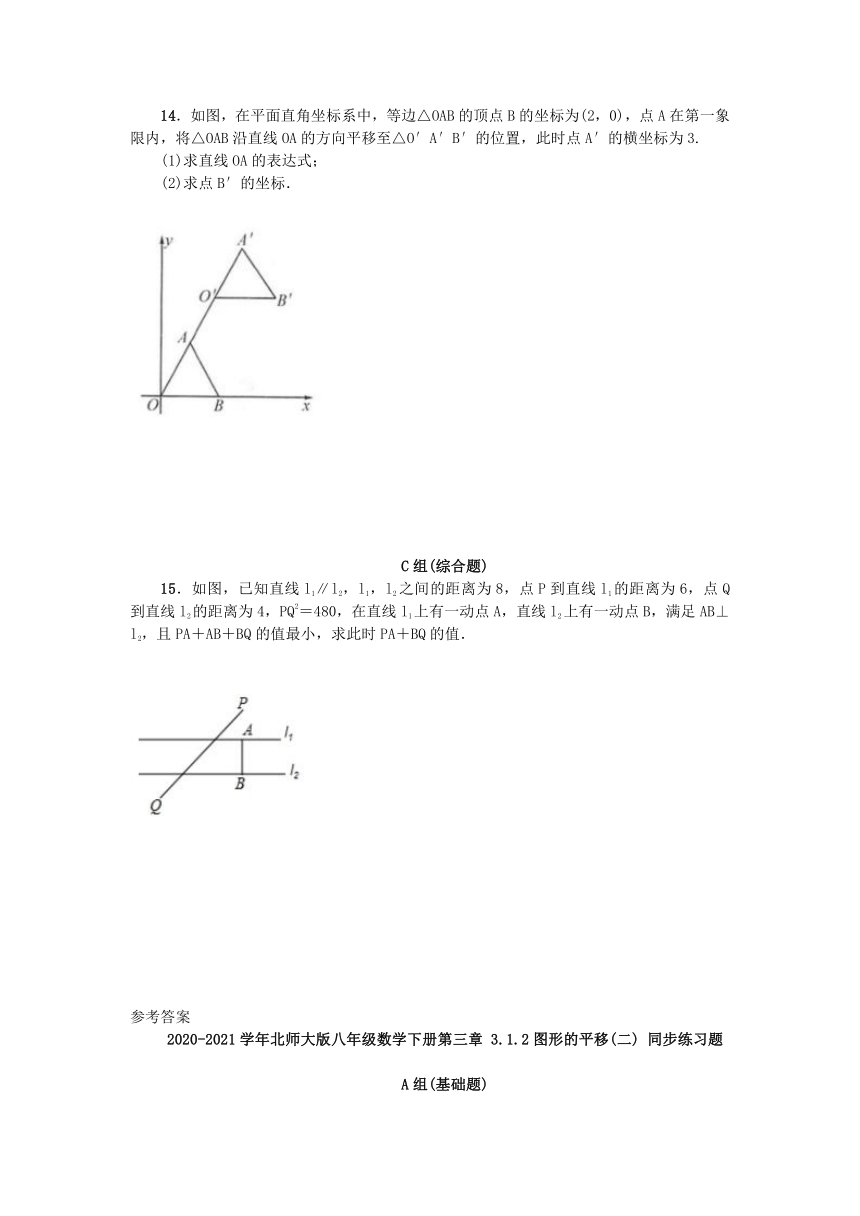
10.如图,经过平移,四边形ABCD的顶点A平移到了点A′.
(1)指出平移的方向和平移的距离;
(2)画出平移后的四边形A′B′C′D′.
B组(中档题)
一、填空题
11.如图,在长20
m,宽10
m的长方形草地内修建了宽2
m的道路,则草地的面积为_____.
12.已知大正方形的边长为5厘米,小正方形的边长为2厘米,起始状态如图所示.大正方形固定不动,把小正方形以1厘米/秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,小正方形平移的时间为_____秒.
13.如图,图形①②③均是以P0为圆心,1个单位长度为半径的扇形,将图形①②③分别沿东北、正南、西北方向同时平移,每次移动1个单位长度,第一次移动后图形①②③的圆心依次为P1,P2,P3,第二次移动后图形①②③的圆心依次为P4,P5,P6,…,依此规律,P0P2
021=_____个单位长度.
二、解答题
14.如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3.
(1)求直线OA的表达式;
(2)求点B′的坐标.
C组(综合题)
15.如图,已知直线l1∥l2,l1,l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ2=480,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ的值最小,求此时PA+BQ的值.
参考答案
2020-2021学年北师大版八年级数学下册第三章
3.1.2图形的平移(二)
同步练习题
A组(基础题)
一、填空题
1.如图,将直线l1沿AB的方向平移得到l2.若∠1=40°,则∠2=40°.
2.如图,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,则在“笑脸”图标中的点P的对应点的坐标是(-1,2).
3.(1)如图,左边的图形是由右边的图形向左平移6个单位长度得到的;
(2)将点P(-4,y)先向左平移2个单位长度,再向下平移3个单位长度后得到点Q(x,-1),则x=-6,y=2.
4.(1)利用平移的知识计算,所给图形的周长为18;
(2)如图,△ABC的顶点都在网格点上,将△ABC向右平移3个单位长度,再向上平移2个单位长度,则平移后得到的△A′B′C′的顶点A′的坐标是(1,3).
二、选择题
5.下列说法正确的是(D)
A.平移改变图形的形状
B.平移改变图形的大小
C.平移改变图形的形状和大小
D.平移不改变图形的形状和大小
6.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都加上3,则所得图形与原图形的关系是:将原图形(B)
A.向左平移3个单位长度
B.向右平移3个单位长度
C.向上平移3个单位长度
D.向下平移3个单位长度
7.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是(C)
A.(1,0)
B.(,)
C.(1,)
D.(-1,)
8.下列图形中,分别把△ABC平移后能得到△DEF的是(A)
三、解答题
9.如图,方格是由边长为1个单位长度的正方形组成的.
(1)求图中阴影部分的面积;
(2)画出△ABC向右平移2个单位长度后得到的图形.
解:(1)S△ABC=×2×3=3.
(2)如图所示,△DEF即为所求.
10.如图,经过平移,四边形ABCD的顶点A平移到了点A′.
(1)指出平移的方向和平移的距离;
(2)画出平移后的四边形A′B′C′D′.
解:(1)如图,连接AA′,平移的方向是点A到点A′的方向,平移的距离是线段AA′的长度.
(2)如图,四边形A′B′C′D′即为所求.
B组(中档题)
一、填空题
11.如图,在长20
m,宽10
m的长方形草地内修建了宽2
m的道路,则草地的面积为144_m2.
12.已知大正方形的边长为5厘米,小正方形的边长为2厘米,起始状态如图所示.大正方形固定不动,把小正方形以1厘米/秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,小正方形平移的时间为1或6秒.
13.如图,图形①②③均是以P0为圆心,1个单位长度为半径的扇形,将图形①②③分别沿东北、正南、西北方向同时平移,每次移动1个单位长度,第一次移动后图形①②③的圆心依次为P1,P2,P3,第二次移动后图形①②③的圆心依次为P4,P5,P6,…,依此规律,P0P2
021=674个单位长度.
二、解答题
14.如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3.
(1)求直线OA的表达式;
(2)求点B′的坐标.
解:(1)过点A作AM⊥x轴于点M.
∵等边△OAB的顶点B的坐标为(2,0),
∴OA=OB=2,∠AOB=60°.
∴OM=OA=1,AM=.
∴A(1,).
∴直线OA的表达式为y=x.
(2)∵直线OA的表达式为y=x,
∴当x=3时,y=3.∴A′(3,3).
∴将点A向右平移2个单位长度,再向上平移2个单位长度后可得点A′.
∴将点B(2,0)向右平移2个单位长度,再向上平移2个单位长度后可得点B′.
∴点B′的坐标为(4,2).
C组(综合题)
15.如图,已知直线l1∥l2,l1,l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ2=480,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ的值最小,求此时PA+BQ的值.
解:作PE⊥l1于点E,交l2于点F,在PF上截取PC=8,连接QC交l2于点B,作BA⊥l1于点A,连接PA,此时PA+AB+BQ最短,作QD⊥PF于点D.
在Rt△PQD中,∵∠D=90°,PQ2=480,PD=6+8+4=18,
∴DQ2=PQ2-PD2=156.
∵AB=PC=8,AB∥PC,
∴AB可由PC平移得到.
∴PA=BC.
∴PA+BQ=BC+BQ=QC==16.
3.1.2图形的平移(二)
同步练习题
A组(基础题)
一、填空题
1.如图,将直线l1沿AB的方向平移得到l2.若∠1=40°,则∠2=_____.
2.如图,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,则在“笑脸”图标中的点P的对应点的坐标是_____.
3.(1)如图,左边的图形是由右边的图形向_____平移_____个单位长度得到的;
(2)将点P(-4,y)先向左平移2个单位长度,再向下平移3个单位长度后得到点Q(x,-1),则x=_____,y=_____.
4.(1)利用平移的知识计算,所给图形的周长为_____;
(2)如图,△ABC的顶点都在网格点上,将△ABC向右平移3个单位长度,再向上平移2个单位长度,则平移后得到的△A′B′C′的顶点A′的坐标是_____.
二、选择题
5.下列说法正确的是(
)
A.平移改变图形的形状
B.平移改变图形的大小
C.平移改变图形的形状和大小
D.平移不改变图形的形状和大小
6.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都加上3,则所得图形与原图形的关系是:将原图形(
)
A.向左平移3个单位长度
B.向右平移3个单位长度
C.向上平移3个单位长度
D.向下平移3个单位长度
7.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是(
)
A.(1,0)
B.(,)
C.(1,)
D.(-1,)
8.下列图形中,分别把△ABC平移后能得到△DEF的是(
)
三、解答题
9.如图,方格是由边长为1个单位长度的正方形组成的.
(1)求图中阴影部分的面积;
(2)画出△ABC向右平移2个单位长度后得到的图形.
10.如图,经过平移,四边形ABCD的顶点A平移到了点A′.
(1)指出平移的方向和平移的距离;
(2)画出平移后的四边形A′B′C′D′.
B组(中档题)
一、填空题
11.如图,在长20
m,宽10
m的长方形草地内修建了宽2
m的道路,则草地的面积为_____.
12.已知大正方形的边长为5厘米,小正方形的边长为2厘米,起始状态如图所示.大正方形固定不动,把小正方形以1厘米/秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,小正方形平移的时间为_____秒.
13.如图,图形①②③均是以P0为圆心,1个单位长度为半径的扇形,将图形①②③分别沿东北、正南、西北方向同时平移,每次移动1个单位长度,第一次移动后图形①②③的圆心依次为P1,P2,P3,第二次移动后图形①②③的圆心依次为P4,P5,P6,…,依此规律,P0P2
021=_____个单位长度.
二、解答题
14.如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3.
(1)求直线OA的表达式;
(2)求点B′的坐标.
C组(综合题)
15.如图,已知直线l1∥l2,l1,l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ2=480,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ的值最小,求此时PA+BQ的值.
参考答案
2020-2021学年北师大版八年级数学下册第三章
3.1.2图形的平移(二)
同步练习题
A组(基础题)
一、填空题
1.如图,将直线l1沿AB的方向平移得到l2.若∠1=40°,则∠2=40°.
2.如图,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,则在“笑脸”图标中的点P的对应点的坐标是(-1,2).
3.(1)如图,左边的图形是由右边的图形向左平移6个单位长度得到的;
(2)将点P(-4,y)先向左平移2个单位长度,再向下平移3个单位长度后得到点Q(x,-1),则x=-6,y=2.
4.(1)利用平移的知识计算,所给图形的周长为18;
(2)如图,△ABC的顶点都在网格点上,将△ABC向右平移3个单位长度,再向上平移2个单位长度,则平移后得到的△A′B′C′的顶点A′的坐标是(1,3).
二、选择题
5.下列说法正确的是(D)
A.平移改变图形的形状
B.平移改变图形的大小
C.平移改变图形的形状和大小
D.平移不改变图形的形状和大小
6.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都加上3,则所得图形与原图形的关系是:将原图形(B)
A.向左平移3个单位长度
B.向右平移3个单位长度
C.向上平移3个单位长度
D.向下平移3个单位长度
7.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是(C)
A.(1,0)
B.(,)
C.(1,)
D.(-1,)
8.下列图形中,分别把△ABC平移后能得到△DEF的是(A)
三、解答题
9.如图,方格是由边长为1个单位长度的正方形组成的.
(1)求图中阴影部分的面积;
(2)画出△ABC向右平移2个单位长度后得到的图形.
解:(1)S△ABC=×2×3=3.
(2)如图所示,△DEF即为所求.
10.如图,经过平移,四边形ABCD的顶点A平移到了点A′.
(1)指出平移的方向和平移的距离;
(2)画出平移后的四边形A′B′C′D′.
解:(1)如图,连接AA′,平移的方向是点A到点A′的方向,平移的距离是线段AA′的长度.
(2)如图,四边形A′B′C′D′即为所求.
B组(中档题)
一、填空题
11.如图,在长20
m,宽10
m的长方形草地内修建了宽2
m的道路,则草地的面积为144_m2.
12.已知大正方形的边长为5厘米,小正方形的边长为2厘米,起始状态如图所示.大正方形固定不动,把小正方形以1厘米/秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,小正方形平移的时间为1或6秒.
13.如图,图形①②③均是以P0为圆心,1个单位长度为半径的扇形,将图形①②③分别沿东北、正南、西北方向同时平移,每次移动1个单位长度,第一次移动后图形①②③的圆心依次为P1,P2,P3,第二次移动后图形①②③的圆心依次为P4,P5,P6,…,依此规律,P0P2
021=674个单位长度.
二、解答题
14.如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3.
(1)求直线OA的表达式;
(2)求点B′的坐标.
解:(1)过点A作AM⊥x轴于点M.
∵等边△OAB的顶点B的坐标为(2,0),
∴OA=OB=2,∠AOB=60°.
∴OM=OA=1,AM=.
∴A(1,).
∴直线OA的表达式为y=x.
(2)∵直线OA的表达式为y=x,
∴当x=3时,y=3.∴A′(3,3).
∴将点A向右平移2个单位长度,再向上平移2个单位长度后可得点A′.
∴将点B(2,0)向右平移2个单位长度,再向上平移2个单位长度后可得点B′.
∴点B′的坐标为(4,2).
C组(综合题)
15.如图,已知直线l1∥l2,l1,l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ2=480,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ的值最小,求此时PA+BQ的值.
解:作PE⊥l1于点E,交l2于点F,在PF上截取PC=8,连接QC交l2于点B,作BA⊥l1于点A,连接PA,此时PA+AB+BQ最短,作QD⊥PF于点D.
在Rt△PQD中,∵∠D=90°,PQ2=480,PD=6+8+4=18,
∴DQ2=PQ2-PD2=156.
∵AB=PC=8,AB∥PC,
∴AB可由PC平移得到.
∴PA=BC.
∴PA+BQ=BC+BQ=QC==16.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
