2020-2021学年北师大版八年级数学下册3.2.1图形的旋转(一) 同步练习题(Word版,附答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册3.2.1图形的旋转(一) 同步练习题(Word版,附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 172.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 09:38:05 | ||
图片预览


文档简介
2020-2021学年北师大版八年级数学下册第三章
3.2.1图形的旋转(一)
同步练习题
A组(基础题)
一、填空题
1.(1)图形的旋转只改变图形的______,而不改变图形的______;
(2)钟表的时针经过20分钟,旋转了______度.
2.如图所示,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形.若点D恰好落在AB上,则∠A的度数为______.
3.如图,钟表的指针AOBC绕中心O按顺时针方向旋转60°得到四边形DOEF,那么四边形DOEF绕中心O按顺时针方向至少旋转______度才能得到四边形AOBC.
4.如图,P是等边△ABC内的一点,且PA=3,PB=4,PC=5.若将△PAC绕点A逆时针旋转后得到△P′AB,则∠APB的度数是______.
二、选择题
5.如图所示,该图案是经过(
)
A.平移得到的
B.旋转或轴对称得到的
C.轴对称得到的
D.旋转得到的
6.有两个直角三角形纸板,一个含45°角,另一个含30°角,如图1所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A顺时针旋转,使BC∥DE,如图2所示,则旋转角∠BAD的度数为(
)
A.15°
B.30°
C.45°
D.60°
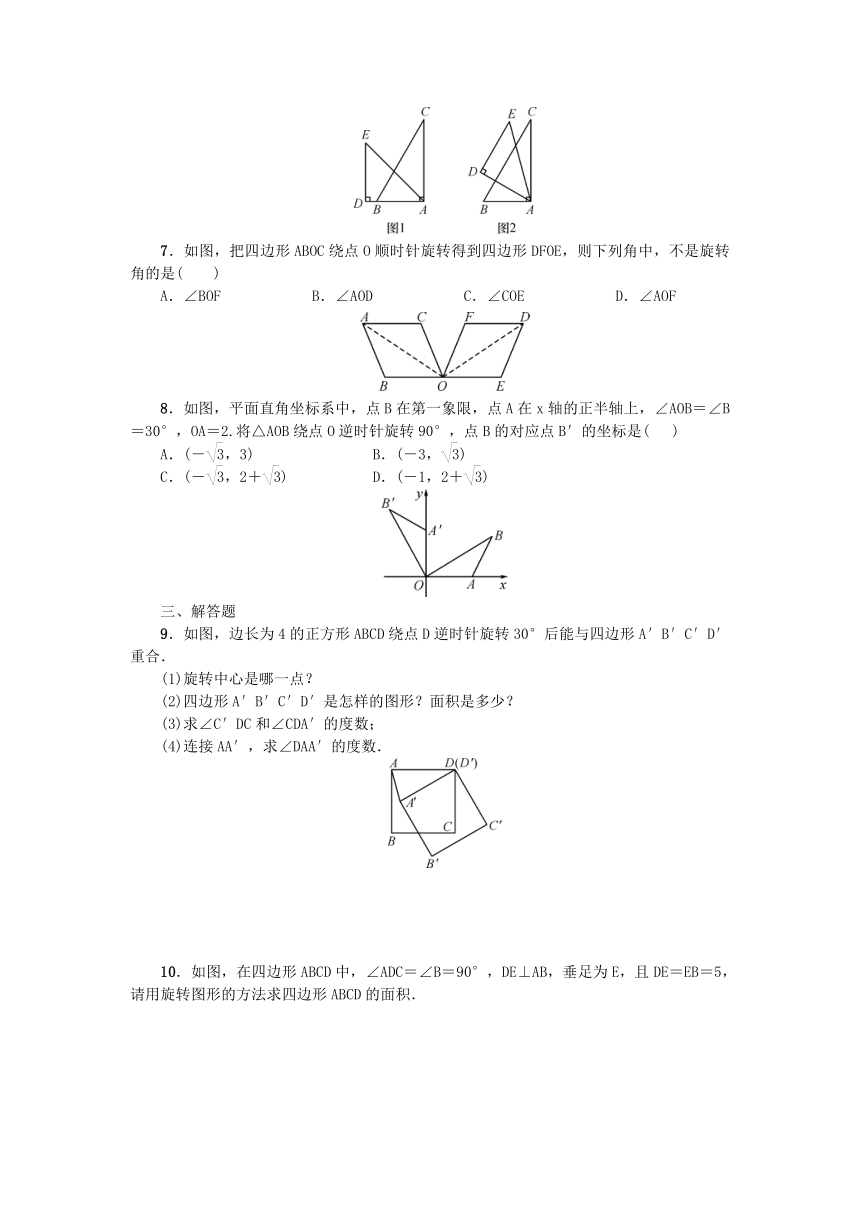
7.如图,把四边形ABOC绕点O顺时针旋转得到四边形DFOE,则下列角中,不是旋转角的是(
)
A.∠BOF
B.∠AOD
C.∠COE
D.∠AOF
8.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是(
)
A.(-,3)
B.(-3,)
C.(-,2+)
D.(-1,2+)
三、解答题
9.如图,边长为4的正方形ABCD绕点D逆时针旋转30°后能与四边形A′B′C′D′重合.
(1)旋转中心是哪一点?
(2)四边形A′B′C′D′是怎样的图形?面积是多少?
(3)求∠C′DC和∠CDA′的度数;
(4)连接AA′,求∠DAA′的度数.
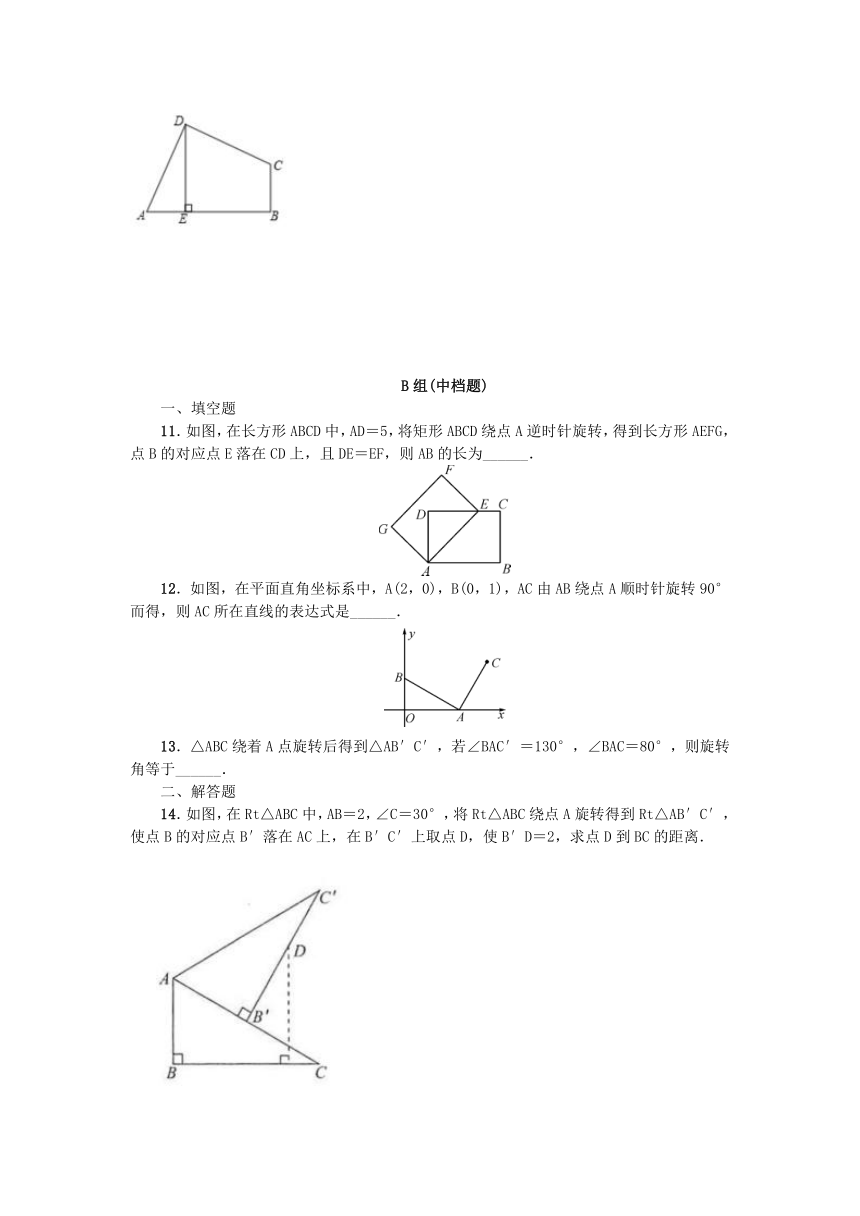
10.如图,在四边形ABCD中,∠ADC=∠B=90°,DE⊥AB,垂足为E,且DE=EB=5,请用旋转图形的方法求四边形ABCD的面积.
B组(中档题)
一、填空题
11.如图,在长方形ABCD中,AD=5,将矩形ABCD绕点A逆时针旋转,得到长方形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为______.
12.如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的表达式是______.
13.△ABC绕着A点旋转后得到△AB′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于______.
二、解答题
14.如图,在Rt△ABC中,AB=2,∠C=30°,将Rt△ABC绕点A旋转得到Rt△AB′C′,使点B的对应点B′落在AC上,在B′C′上取点D,使B′D=2,求点D到BC的距离.
C组(综合题)
15.如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA,OB相交于点D,E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OD+OE与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给予证明;若不成立,线段OD,OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
参考答案
2020-2021学年北师大版八年级数学下册第三章
3.2.1图形的旋转(一)
同步练习题
A组(基础题)
一、填空题
1.(1)图形的旋转只改变图形的位置,而不改变图形的形状和大小;
(2)钟表的时针经过20分钟,旋转了10度.
2.如图所示,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形.若点D恰好落在AB上,则∠A的度数为75°.
3.如图,钟表的指针AOBC绕中心O按顺时针方向旋转60°得到四边形DOEF,那么四边形DOEF绕中心O按顺时针方向至少旋转300度才能得到四边形AOBC.
4.如图,P是等边△ABC内的一点,且PA=3,PB=4,PC=5.若将△PAC绕点A逆时针旋转后得到△P′AB,则∠APB的度数是150°.
二、选择题
5.如图所示,该图案是经过(B)
A.平移得到的
B.旋转或轴对称得到的
C.轴对称得到的
D.旋转得到的
6.有两个直角三角形纸板,一个含45°角,另一个含30°角,如图1所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A顺时针旋转,使BC∥DE,如图2所示,则旋转角∠BAD的度数为(B)
A.15°
B.30°
C.45°
D.60°
7.如图,把四边形ABOC绕点O顺时针旋转得到四边形DFOE,则下列角中,不是旋转角的是(D)
A.∠BOF
B.∠AOD
C.∠COE
D.∠AOF
8.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是(A)
A.(-,3)
B.(-3,)
C.(-,2+)
D.(-1,2+)
三、解答题
9.如图,边长为4的正方形ABCD绕点D逆时针旋转30°后能与四边形A′B′C′D′重合.
(1)旋转中心是哪一点?
(2)四边形A′B′C′D′是怎样的图形?面积是多少?
(3)求∠C′DC和∠CDA′的度数;
(4)连接AA′,求∠DAA′的度数.
解:(1)旋转中心是点D.
(2)四边形A′B′C′D′是正方形.
∵正方形ABCD的面积为16,
∴四边形A′B′C′D′的面积是16.
(3)∵C与C′是对应点,且对应点与旋转中心连线所成的角即是旋转角,由题意知图形绕点D旋转30°,∴∠C′DC=30°.
∵四边形A′B′C′D′是正方形,
∴∠C′DA′=90°.
∴∠CDA′=60°.
(4)根据旋转的特征,知AD=A′D.
∵∠ADA′=30°,
∴∠DAA′=∠DA′A=(180°-30°)÷2=75°.
10.如图,在四边形ABCD中,∠ADC=∠B=90°,DE⊥AB,垂足为E,且DE=EB=5,请用旋转图形的方法求四边形ABCD的面积.
解:把△ADE绕点D逆时针旋转90°后,得到的图形为边长是5的正方形DEBF,则四边形ABCD的面积等于正方形DEBF的面积,为25.
B组(中档题)
一、填空题
11.如图,在长方形ABCD中,AD=5,将矩形ABCD绕点A逆时针旋转,得到长方形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为5.
12.如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的表达式是y=2x-4.
13.△ABC绕着A点旋转后得到△AB′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于50°或210°.
二、解答题
14.如图,在Rt△ABC中,AB=2,∠C=30°,将Rt△ABC绕点A旋转得到Rt△AB′C′,使点B的对应点B′落在AC上,在B′C′上取点D,使B′D=2,求点D到BC的距离.
解:∵在Rt△ABC中,AB=2,∠C=30°,∴AC=4,BC=2.
∵将Rt△ABC绕点A旋转得到Rt△AB′C′,使点B的对应点B′落在AC上,
∴AB′=AB=2.
∴B′C=2.
延长C′B′交BC于点F,
∴∠CB′F=∠AB′C′=90°.
∵∠C=30°,∴∠CFB′=60°,CF=,B′F=.
∵B′D=2,∴DF=2+.
过点D作DE⊥BC于点E,
∴EF=DF=1+,DE=+1.
∴点D到BC的距离为+1.
C组(综合题)
15.如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA,OB相交于点D,E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OD+OE与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给予证明;若不成立,线段OD,OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
解:(1)OD+OE=OC.理由:
∵OM是∠AOB的平分线,
∴∠AOC=∠BOC=∠AOB=30°.
∵CD⊥OA,
∴∠ODC=90°.∴∠OCD=60°.
∴∠OCE=∠DCE-∠OCD=60°.
在Rt△OCD中,∠COD=30°,∴OC=2CD.
由勾股定理,得OD=OC.
同理:OE=OC.
∴OD+OE=OC.
(2)(1)中结论仍然成立.理由:
过点C作CF⊥OA于点F,CG⊥OB于点G,
∴∠OFC=∠OGC=90°.
∵∠AOB=60°,∴∠FCG=120°.
同(1)的方法,得OF=OC,OG=OC.
∴OF+OG=OC.
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,
∴CF=CG.
∵∠DCE=120°,∠FCG=120°,∴∠DCF=∠ECG.
∴△CFD≌△CGE(ASA).
∴DF=EG.
∴OF=OD+DF=OD+EG,OG=OE-EG.
∴OF+OG=OD+EG+OE-EG=OD+OE.
∴OD+OE=OC.
(3)如图3,(1)中结论不成立,结论为:OE-OD=OC.
3.2.1图形的旋转(一)
同步练习题
A组(基础题)
一、填空题
1.(1)图形的旋转只改变图形的______,而不改变图形的______;
(2)钟表的时针经过20分钟,旋转了______度.
2.如图所示,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形.若点D恰好落在AB上,则∠A的度数为______.
3.如图,钟表的指针AOBC绕中心O按顺时针方向旋转60°得到四边形DOEF,那么四边形DOEF绕中心O按顺时针方向至少旋转______度才能得到四边形AOBC.
4.如图,P是等边△ABC内的一点,且PA=3,PB=4,PC=5.若将△PAC绕点A逆时针旋转后得到△P′AB,则∠APB的度数是______.
二、选择题
5.如图所示,该图案是经过(
)
A.平移得到的
B.旋转或轴对称得到的
C.轴对称得到的
D.旋转得到的
6.有两个直角三角形纸板,一个含45°角,另一个含30°角,如图1所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A顺时针旋转,使BC∥DE,如图2所示,则旋转角∠BAD的度数为(
)
A.15°
B.30°
C.45°
D.60°
7.如图,把四边形ABOC绕点O顺时针旋转得到四边形DFOE,则下列角中,不是旋转角的是(
)
A.∠BOF
B.∠AOD
C.∠COE
D.∠AOF
8.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是(
)
A.(-,3)
B.(-3,)
C.(-,2+)
D.(-1,2+)
三、解答题
9.如图,边长为4的正方形ABCD绕点D逆时针旋转30°后能与四边形A′B′C′D′重合.
(1)旋转中心是哪一点?
(2)四边形A′B′C′D′是怎样的图形?面积是多少?
(3)求∠C′DC和∠CDA′的度数;
(4)连接AA′,求∠DAA′的度数.
10.如图,在四边形ABCD中,∠ADC=∠B=90°,DE⊥AB,垂足为E,且DE=EB=5,请用旋转图形的方法求四边形ABCD的面积.
B组(中档题)
一、填空题
11.如图,在长方形ABCD中,AD=5,将矩形ABCD绕点A逆时针旋转,得到长方形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为______.
12.如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的表达式是______.
13.△ABC绕着A点旋转后得到△AB′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于______.
二、解答题
14.如图,在Rt△ABC中,AB=2,∠C=30°,将Rt△ABC绕点A旋转得到Rt△AB′C′,使点B的对应点B′落在AC上,在B′C′上取点D,使B′D=2,求点D到BC的距离.
C组(综合题)
15.如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA,OB相交于点D,E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OD+OE与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给予证明;若不成立,线段OD,OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
参考答案
2020-2021学年北师大版八年级数学下册第三章
3.2.1图形的旋转(一)
同步练习题
A组(基础题)
一、填空题
1.(1)图形的旋转只改变图形的位置,而不改变图形的形状和大小;
(2)钟表的时针经过20分钟,旋转了10度.
2.如图所示,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形.若点D恰好落在AB上,则∠A的度数为75°.
3.如图,钟表的指针AOBC绕中心O按顺时针方向旋转60°得到四边形DOEF,那么四边形DOEF绕中心O按顺时针方向至少旋转300度才能得到四边形AOBC.
4.如图,P是等边△ABC内的一点,且PA=3,PB=4,PC=5.若将△PAC绕点A逆时针旋转后得到△P′AB,则∠APB的度数是150°.
二、选择题
5.如图所示,该图案是经过(B)
A.平移得到的
B.旋转或轴对称得到的
C.轴对称得到的
D.旋转得到的
6.有两个直角三角形纸板,一个含45°角,另一个含30°角,如图1所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A顺时针旋转,使BC∥DE,如图2所示,则旋转角∠BAD的度数为(B)
A.15°
B.30°
C.45°
D.60°
7.如图,把四边形ABOC绕点O顺时针旋转得到四边形DFOE,则下列角中,不是旋转角的是(D)
A.∠BOF
B.∠AOD
C.∠COE
D.∠AOF
8.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是(A)
A.(-,3)
B.(-3,)
C.(-,2+)
D.(-1,2+)
三、解答题
9.如图,边长为4的正方形ABCD绕点D逆时针旋转30°后能与四边形A′B′C′D′重合.
(1)旋转中心是哪一点?
(2)四边形A′B′C′D′是怎样的图形?面积是多少?
(3)求∠C′DC和∠CDA′的度数;
(4)连接AA′,求∠DAA′的度数.
解:(1)旋转中心是点D.
(2)四边形A′B′C′D′是正方形.
∵正方形ABCD的面积为16,
∴四边形A′B′C′D′的面积是16.
(3)∵C与C′是对应点,且对应点与旋转中心连线所成的角即是旋转角,由题意知图形绕点D旋转30°,∴∠C′DC=30°.
∵四边形A′B′C′D′是正方形,
∴∠C′DA′=90°.
∴∠CDA′=60°.
(4)根据旋转的特征,知AD=A′D.
∵∠ADA′=30°,
∴∠DAA′=∠DA′A=(180°-30°)÷2=75°.
10.如图,在四边形ABCD中,∠ADC=∠B=90°,DE⊥AB,垂足为E,且DE=EB=5,请用旋转图形的方法求四边形ABCD的面积.
解:把△ADE绕点D逆时针旋转90°后,得到的图形为边长是5的正方形DEBF,则四边形ABCD的面积等于正方形DEBF的面积,为25.
B组(中档题)
一、填空题
11.如图,在长方形ABCD中,AD=5,将矩形ABCD绕点A逆时针旋转,得到长方形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为5.
12.如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的表达式是y=2x-4.
13.△ABC绕着A点旋转后得到△AB′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于50°或210°.
二、解答题
14.如图,在Rt△ABC中,AB=2,∠C=30°,将Rt△ABC绕点A旋转得到Rt△AB′C′,使点B的对应点B′落在AC上,在B′C′上取点D,使B′D=2,求点D到BC的距离.
解:∵在Rt△ABC中,AB=2,∠C=30°,∴AC=4,BC=2.
∵将Rt△ABC绕点A旋转得到Rt△AB′C′,使点B的对应点B′落在AC上,
∴AB′=AB=2.
∴B′C=2.
延长C′B′交BC于点F,
∴∠CB′F=∠AB′C′=90°.
∵∠C=30°,∴∠CFB′=60°,CF=,B′F=.
∵B′D=2,∴DF=2+.
过点D作DE⊥BC于点E,
∴EF=DF=1+,DE=+1.
∴点D到BC的距离为+1.
C组(综合题)
15.如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA,OB相交于点D,E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OD+OE与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给予证明;若不成立,线段OD,OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
解:(1)OD+OE=OC.理由:
∵OM是∠AOB的平分线,
∴∠AOC=∠BOC=∠AOB=30°.
∵CD⊥OA,
∴∠ODC=90°.∴∠OCD=60°.
∴∠OCE=∠DCE-∠OCD=60°.
在Rt△OCD中,∠COD=30°,∴OC=2CD.
由勾股定理,得OD=OC.
同理:OE=OC.
∴OD+OE=OC.
(2)(1)中结论仍然成立.理由:
过点C作CF⊥OA于点F,CG⊥OB于点G,
∴∠OFC=∠OGC=90°.
∵∠AOB=60°,∴∠FCG=120°.
同(1)的方法,得OF=OC,OG=OC.
∴OF+OG=OC.
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,
∴CF=CG.
∵∠DCE=120°,∠FCG=120°,∴∠DCF=∠ECG.
∴△CFD≌△CGE(ASA).
∴DF=EG.
∴OF=OD+DF=OD+EG,OG=OE-EG.
∴OF+OG=OD+EG+OE-EG=OD+OE.
∴OD+OE=OC.
(3)如图3,(1)中结论不成立,结论为:OE-OD=OC.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
