2020-2021学年北师大版八年级数学下册3.1.1图形的平移(一) 同步练习题(Word版,附答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册3.1.1图形的平移(一) 同步练习题(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 109.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 09:30:32 | ||
图片预览



文档简介
2020-2021学年北师大版八年级数学下册第三章
3.1.1图形的平移(一)
同步练习题
A组(基础题)
一、填空题
1.(1)平移不改变图形的_______和_______;
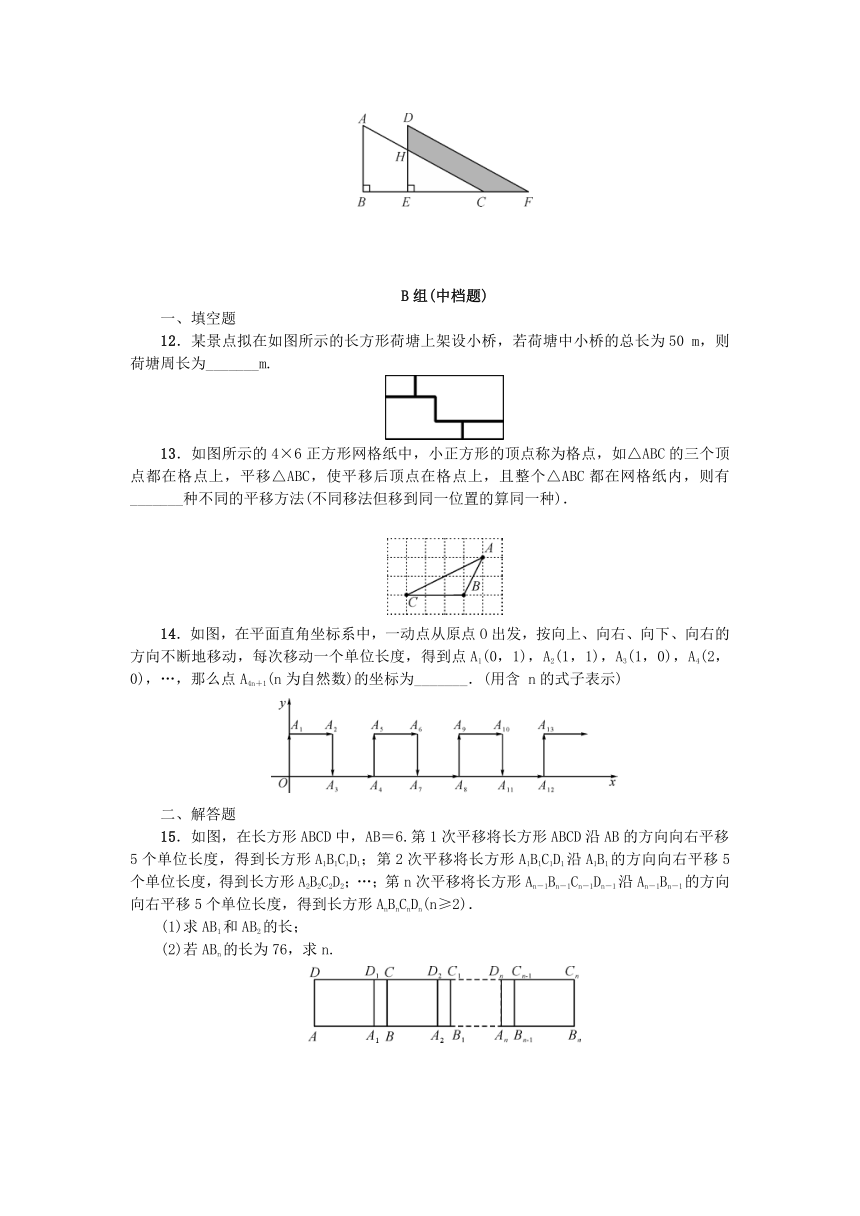
(2)如图,△ADE是由△DBF沿BD所在的直线平移得到的,AE,BF的延长线交于点C.若∠BFD=30°,则∠C的度数是_______.
2.(1)高铁在笔直的铁路上开动,高铁车头以350千米/时的速度前进了半小时,则车尾走的路程是_______千米;
(2)平移后图形的位置是______________所决定.
3.如图,△ABC沿MN方向平移5
cm后成为△DEF,那么点A的对应点是点_______.
4.如图,已知∠ABC=45°,AB=4,把线段AB向右平移7个单位长度得到A′B′,则四边形ABB′A′的面积是_______.
5.如图,将周长为8的△ABC沿BC边向右平移2个单位长度,得到△DEF,则四边形ABFD的周长为_______.
二、选择题
6.下列运动属于平移的有(
)
①水平运输带上的砖的运动;②啤酒生产线上的啤酒瓶通过压盖机前后的运动;③升降机上下做机械运动;④足球场上足球的运动.
A.1种
B.2种
C.3种
D.4种
7.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是(
)
A.平行四边形
B.等腰梯形
C.正六边形
D.圆
8.如图所示的每个图形中的两个三角形是经过平移得到的是(
)
9.如图,一个圆柱体在正方体上沿虚线从左向右平移,平移过程中不变的是(
)
A.主视图
B.左视图
C.俯视图
D.主视图和俯视图
三、解答题
10.如图,已知A′B′是△ABC平移后AB的对应线段,请你作出平移后的△A′B′C′.
11.(1)如图,将△ABC沿BC的方向平移得到△DEF.
①若∠B=74°,∠F=26°,求∠A的度数;
②若BC=4.5
cm,EC=3.5
cm,求△ABC平移的距离.
(2)如图,将△ABC沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移的距离为4,求阴影部分的面积.
B组(中档题)
一、填空题
12.某景点拟在如图所示的长方形荷塘上架设小桥,若荷塘中小桥的总长为50
m,则荷塘周长为_______m.
13.如图所示的4×6正方形网格纸中,小正方形的顶点称为格点,如△ABC的三个顶点都在格点上,平移△ABC,使平移后顶点在格点上,且整个△ABC都在网格纸内,则有_______种不同的平移方法(不同移法但移到同一位置的算同一种).
14.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每次移动一个单位长度,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为_______.(用含
n的式子表示)
二、解答题
15.如图,在长方形ABCD中,AB=6.第1次平移将长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1;第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2;…;第n次平移将长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n≥2).
(1)求AB1和AB2的长;
(2)若ABn的长为76,求n.
C组(综合题)
如图,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,CE是由AB平移所得.求证:AC+BD≥AB.
参考答案
2020-2021学年北师大版八年级数学下册第三章
3.1.1图形的平移(一)
同步练习题
A组(基础题)
一、填空题
1.(1)平移不改变图形的形状和大小;
(2)如图,△ADE是由△DBF沿BD所在的直线平移得到的,AE,BF的延长线交于点C.若∠BFD=30°,则∠C的度数是30°.
2.(1)高铁在笔直的铁路上开动,高铁车头以350千米/时的速度前进了半小时,则车尾走的路程是175千米;
(2)平移后图形的位置是由平移的方向和平移的距离所决定.
3.如图,△ABC沿MN方向平移5
cm后成为△DEF,那么点A的对应点是点D.
4.如图,已知∠ABC=45°,AB=4,把线段AB向右平移7个单位长度得到A′B′,则四边形ABB′A′的面积是28.
5.如图,将周长为8的△ABC沿BC边向右平移2个单位长度,得到△DEF,则四边形ABFD的周长为12.
二、选择题
6.下列运动属于平移的有(C)
①水平运输带上的砖的运动;②啤酒生产线上的啤酒瓶通过压盖机前后的运动;③升降机上下做机械运动;④足球场上足球的运动.
A.1种
B.2种
C.3种
D.4种
7.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是(A)
A.平行四边形
B.等腰梯形
C.正六边形
D.圆
8.如图所示的每个图形中的两个三角形是经过平移得到的是(D)
9.如图,一个圆柱体在正方体上沿虚线从左向右平移,平移过程中不变的是(B)
A.主视图
B.左视图
C.俯视图
D.主视图和俯视图
三、解答题
10.如图,已知A′B′是△ABC平移后AB的对应线段,请你作出平移后的△A′B′C′.
解:如图所示.作法:
(1)连接BB′;
(2)过点C作CF∥BB′;
(3)在CF上截取CC′=BB′;
(4)连接B′C′,A′C′.
则△A′B′C′就是求作的图形.
11.(1)如图,将△ABC沿BC的方向平移得到△DEF.
①若∠B=74°,∠F=26°,求∠A的度数;
②若BC=4.5
cm,EC=3.5
cm,求△ABC平移的距离.
解:①由图形平移的特征可知△ABC≌△DEF,
∴∠2=∠F=26°.
∵∠B=74°,
∴∠A=180°-(∠2+∠B)
=180°-(26°+74°)
=80°.
②∵BC=4.5
cm,EC=3.5
cm,
∴BE=BC-EC=4.5-3.5=1(cm).
∴△ABC平移的距离为1
cm.
(2)如图,将△ABC沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移的距离为4,求阴影部分的面积.
解:∵平移的距离为4,
∴BE=4.
∵AB=8,DH=3,
∴EH=8-3=5.
∵S△ABC=S△DEF,∴S四边形ABEH=S阴影.
∴S阴影=×(8+5)×4=26.
B组(中档题)
一、填空题
12.某景点拟在如图所示的长方形荷塘上架设小桥,若荷塘中小桥的总长为50
m,则荷塘周长为100m.
13.如图所示的4×6正方形网格纸中,小正方形的顶点称为格点,如△ABC的三个顶点都在格点上,平移△ABC,使平移后顶点在格点上,且整个△ABC都在网格纸内,则有8种不同的平移方法(不同移法但移到同一位置的算同一种).
14.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每次移动一个单位长度,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为(2n,1).(用含
n的式子表示)
二、解答题
15.如图,在长方形ABCD中,AB=6.第1次平移将长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1;第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2;…;第n次平移将长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n≥2).
(1)求AB1和AB2的长;
(2)若ABn的长为76,求n.
解:(1)由题意,得点B向右平移5个单位长度到达点B1,所以AB1=6+5=11;点B1再向右平移5个单位长度到达点B2,所以AB2=11+5=16.
(2)由(1)知AB1=6+5,AB2=6+2×5,依此类推,AB3=6+3×5,…,ABn=6+5n.
当ABn=6+5n=76时,n=14.
C组(综合题)
16.如图,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,CE是由AB平移所得.求证:AC+BD≥AB.
证明:由题意,得AB=CE,AB∥CE,AC=BE.
∴∠OCE=∠AOC=60°.
又∵CD=AB,∴CE=CD.
连接DE,则△CDE是等边三角形.
∴CD=DE=CE=AB.
∵BD+BE>DE,
∴BD+AC>AB.
当AC∥BD时,BD+AC=AB,
∴AC+BD≥AB.
3.1.1图形的平移(一)
同步练习题
A组(基础题)
一、填空题
1.(1)平移不改变图形的_______和_______;
(2)如图,△ADE是由△DBF沿BD所在的直线平移得到的,AE,BF的延长线交于点C.若∠BFD=30°,则∠C的度数是_______.
2.(1)高铁在笔直的铁路上开动,高铁车头以350千米/时的速度前进了半小时,则车尾走的路程是_______千米;
(2)平移后图形的位置是______________所决定.
3.如图,△ABC沿MN方向平移5
cm后成为△DEF,那么点A的对应点是点_______.
4.如图,已知∠ABC=45°,AB=4,把线段AB向右平移7个单位长度得到A′B′,则四边形ABB′A′的面积是_______.
5.如图,将周长为8的△ABC沿BC边向右平移2个单位长度,得到△DEF,则四边形ABFD的周长为_______.
二、选择题
6.下列运动属于平移的有(
)
①水平运输带上的砖的运动;②啤酒生产线上的啤酒瓶通过压盖机前后的运动;③升降机上下做机械运动;④足球场上足球的运动.
A.1种
B.2种
C.3种
D.4种
7.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是(
)
A.平行四边形
B.等腰梯形
C.正六边形
D.圆
8.如图所示的每个图形中的两个三角形是经过平移得到的是(
)
9.如图,一个圆柱体在正方体上沿虚线从左向右平移,平移过程中不变的是(
)
A.主视图
B.左视图
C.俯视图
D.主视图和俯视图
三、解答题
10.如图,已知A′B′是△ABC平移后AB的对应线段,请你作出平移后的△A′B′C′.
11.(1)如图,将△ABC沿BC的方向平移得到△DEF.
①若∠B=74°,∠F=26°,求∠A的度数;
②若BC=4.5
cm,EC=3.5
cm,求△ABC平移的距离.
(2)如图,将△ABC沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移的距离为4,求阴影部分的面积.
B组(中档题)
一、填空题
12.某景点拟在如图所示的长方形荷塘上架设小桥,若荷塘中小桥的总长为50
m,则荷塘周长为_______m.
13.如图所示的4×6正方形网格纸中,小正方形的顶点称为格点,如△ABC的三个顶点都在格点上,平移△ABC,使平移后顶点在格点上,且整个△ABC都在网格纸内,则有_______种不同的平移方法(不同移法但移到同一位置的算同一种).
14.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每次移动一个单位长度,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为_______.(用含
n的式子表示)
二、解答题
15.如图,在长方形ABCD中,AB=6.第1次平移将长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1;第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2;…;第n次平移将长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n≥2).
(1)求AB1和AB2的长;
(2)若ABn的长为76,求n.
C组(综合题)
如图,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,CE是由AB平移所得.求证:AC+BD≥AB.
参考答案
2020-2021学年北师大版八年级数学下册第三章
3.1.1图形的平移(一)
同步练习题
A组(基础题)
一、填空题
1.(1)平移不改变图形的形状和大小;
(2)如图,△ADE是由△DBF沿BD所在的直线平移得到的,AE,BF的延长线交于点C.若∠BFD=30°,则∠C的度数是30°.
2.(1)高铁在笔直的铁路上开动,高铁车头以350千米/时的速度前进了半小时,则车尾走的路程是175千米;
(2)平移后图形的位置是由平移的方向和平移的距离所决定.
3.如图,△ABC沿MN方向平移5
cm后成为△DEF,那么点A的对应点是点D.
4.如图,已知∠ABC=45°,AB=4,把线段AB向右平移7个单位长度得到A′B′,则四边形ABB′A′的面积是28.
5.如图,将周长为8的△ABC沿BC边向右平移2个单位长度,得到△DEF,则四边形ABFD的周长为12.
二、选择题
6.下列运动属于平移的有(C)
①水平运输带上的砖的运动;②啤酒生产线上的啤酒瓶通过压盖机前后的运动;③升降机上下做机械运动;④足球场上足球的运动.
A.1种
B.2种
C.3种
D.4种
7.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是(A)
A.平行四边形
B.等腰梯形
C.正六边形
D.圆
8.如图所示的每个图形中的两个三角形是经过平移得到的是(D)
9.如图,一个圆柱体在正方体上沿虚线从左向右平移,平移过程中不变的是(B)
A.主视图
B.左视图
C.俯视图
D.主视图和俯视图
三、解答题
10.如图,已知A′B′是△ABC平移后AB的对应线段,请你作出平移后的△A′B′C′.
解:如图所示.作法:
(1)连接BB′;
(2)过点C作CF∥BB′;
(3)在CF上截取CC′=BB′;
(4)连接B′C′,A′C′.
则△A′B′C′就是求作的图形.
11.(1)如图,将△ABC沿BC的方向平移得到△DEF.
①若∠B=74°,∠F=26°,求∠A的度数;
②若BC=4.5
cm,EC=3.5
cm,求△ABC平移的距离.
解:①由图形平移的特征可知△ABC≌△DEF,
∴∠2=∠F=26°.
∵∠B=74°,
∴∠A=180°-(∠2+∠B)
=180°-(26°+74°)
=80°.
②∵BC=4.5
cm,EC=3.5
cm,
∴BE=BC-EC=4.5-3.5=1(cm).
∴△ABC平移的距离为1
cm.
(2)如图,将△ABC沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移的距离为4,求阴影部分的面积.
解:∵平移的距离为4,
∴BE=4.
∵AB=8,DH=3,
∴EH=8-3=5.
∵S△ABC=S△DEF,∴S四边形ABEH=S阴影.
∴S阴影=×(8+5)×4=26.
B组(中档题)
一、填空题
12.某景点拟在如图所示的长方形荷塘上架设小桥,若荷塘中小桥的总长为50
m,则荷塘周长为100m.
13.如图所示的4×6正方形网格纸中,小正方形的顶点称为格点,如△ABC的三个顶点都在格点上,平移△ABC,使平移后顶点在格点上,且整个△ABC都在网格纸内,则有8种不同的平移方法(不同移法但移到同一位置的算同一种).
14.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每次移动一个单位长度,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为(2n,1).(用含
n的式子表示)
二、解答题
15.如图,在长方形ABCD中,AB=6.第1次平移将长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1;第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2;…;第n次平移将长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n≥2).
(1)求AB1和AB2的长;
(2)若ABn的长为76,求n.
解:(1)由题意,得点B向右平移5个单位长度到达点B1,所以AB1=6+5=11;点B1再向右平移5个单位长度到达点B2,所以AB2=11+5=16.
(2)由(1)知AB1=6+5,AB2=6+2×5,依此类推,AB3=6+3×5,…,ABn=6+5n.
当ABn=6+5n=76时,n=14.
C组(综合题)
16.如图,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,CE是由AB平移所得.求证:AC+BD≥AB.
证明:由题意,得AB=CE,AB∥CE,AC=BE.
∴∠OCE=∠AOC=60°.
又∵CD=AB,∴CE=CD.
连接DE,则△CDE是等边三角形.
∴CD=DE=CE=AB.
∵BD+BE>DE,
∴BD+AC>AB.
当AC∥BD时,BD+AC=AB,
∴AC+BD≥AB.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
