2020-2021学年高一数学人教A版必修4第二章 (平面向量)本章小结课件(共86张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修4第二章 (平面向量)本章小结课件(共86张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 22:44:07 | ||
图片预览











文档简介
第二章
平面向量
本章内容
2.1 平面向量的实际背景及基本概念
2.2 平面向量的线性运算
2.3 平面向量的基本定理及坐标表示
2.4 平面向量的数量积
2.5 平面向量应用举例
第二章 小结
本章小结
本章小结
知识要点
例题选讲
复习参考题
自我检测题
知识要点
1. 向量的基本概念
返回目录
向量用有向线段表示.
② 用印刷黑体小写字母表示, 如 a、b、c.
① 用端点的大写字母表示, 如
③ 用书写体加箭头表示, 如
字母表示有三种方法:
向量的大小叫做向量的模,
A
B
3
如:
用有向线段的长度表示,
知识要点
1. 向量的基本概念
◆模为零的向量称为零向量.
◆模为一个单位的向量称为单位向量.
零向量记作 0 ( ).
零向量的方向是任意的.
◆长度相等, 方向相同的向量叫做相等向量.
知识要点
2. 向量加减法
(1) 几何运算
加法的平行四边形法则、三角形法则.
减法的三角形法则 (同起点向量相减).
(2) 代数运算
知识要点
3. 向量的数乘
l>0 时,
与 同向.
l<0 时,
与 反向.
(l?R) 表示 l 个 相加.
知识要点
4. 共线向量
一组平行向量称为共线向量.
共线向量的方向相同或相反.
若 A、B、C 三点共线, 则
(l+m =1).
知识要点
5. 向量基本定理
不共线 (基底),
任一向量
(l, m?R).
知识要点
6. 向量的坐标表示
为 x 轴, y 轴方向的单位向量,
A(x1, y1), B(x2, y2),
O(0, 0), P(x, y),
知识要点
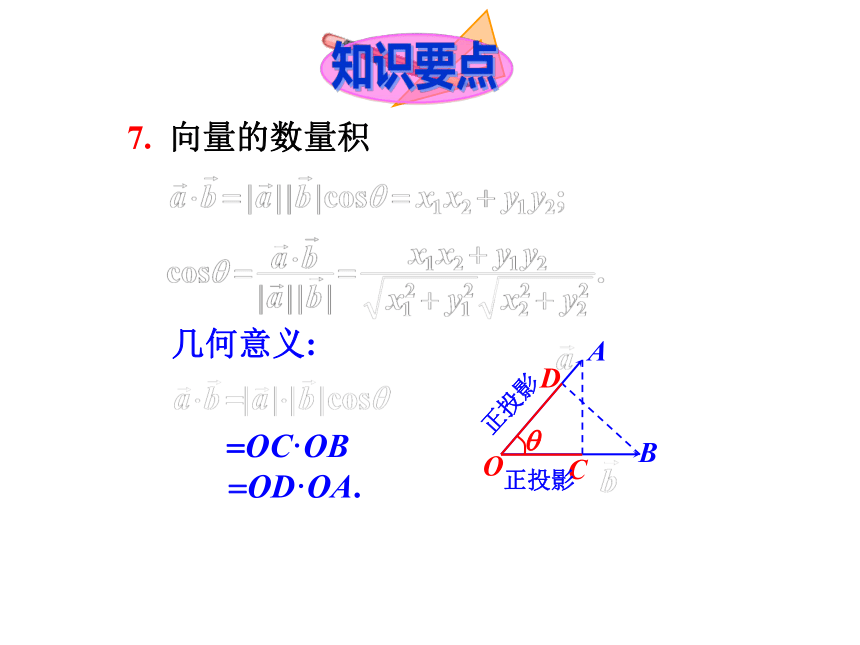
7. 向量的数量积
=OC·OB
=OD·OA.
q
D
O
C
A
B
正投影
正投影
几何意义:
知识要点
8. 数量积的运算定律
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
(a·b)·c≠a·(b·c).
知识要点
9. 向量共线与垂直
a⊥b ?? x1x2+y1y2=0.
a//b ?? b=la(l?R).
a//b ?? x1y2-x2y1=0
知识要点
10. 分点与距离
P(x, y), P1(x1, y1), P2(x2, y2),
P 为中点:
例1. 求证: 直径上的圆周角为直角.
例题选讲
O
·
A
B
C
如图, 已知 AB 是⊙O 的直径, C 是圆上的点. 求证: ∠ACB 为直角.
分析:
目标:
证
向量运算结果为 0 的有
思考将 用向量加减法转换到 上来.
返回目录
例1. 求证: 直径上的圆周角为直角.
例题选讲
O
·
A
B
C
如图, 已知 AB 是⊙O 的直径, C 是圆上的点. 求证: ∠ACB 为直角.
证明:
即
∴∠ACB 是直角.
提取公因式
相反向量
例2. 如图, AD、BE、CF 是△ABC 的三条高. 求证: AD、BE、CF 相交于一点.
A
B
C
D
E
F
思路:
(1) 先定两条高交于一点,
如 BE 与 CF 交于点 H.
(2) 如果 AH⊥BC, 即得三条
高共点.
H
目标:
方法:
将 和 用互相垂直的向量运算代替.
例2. 如图, AD、BE、CF 是△ABC 的三条高. 求证: AD、BE、CF 相交于一点.
A
B
C
D
E
F
证明:
设 BE 与 CF 交于点 H.
H
∵CF⊥AB, BE⊥AC,
=0.
得 AH⊥BC,
∴三条高交于一点.
例3. 如图, 在平行四边形 ABCD 中, AP⊥BD,垂足为 P, 且 AP=3, 则
A
B
C
D
P
分析:
题设中除了一个垂直
关系外, 只有一个已知量,
所求问题需向着已知量转化.
根据垂直关系以及向量数量积的几何意义,
思考已知量 AP 是哪些向量的正投影.
于是可找到
问题就变为将 转化到
例3. 如图, 在平行四边形 ABCD 中, AP⊥BD,垂足为 P, 且 AP=3, 则
A
B
C
D
P
解:
∵AP⊥BD,
=18.
18
例4. 在直角三角形 ABC 中, 点 D 是斜边 AB 的
中点, 点 P 为线段 CD 的中点, 则
(A) 2 (B) 4 (C) 5 (D) 10
分析:
(1) PA, PB, PC 有什么关系?
如图,
A
B
C
D
P
将上式平方有可能达到目标.
(2) 另一运算
平方上式也可能达到目标.
由这两条路切入一试.
例4. 在直角三角形 ABC 中, 点 D 是斜边 AB 的
中点, 点 P 为线段 CD 的中点, 则
(A) 2 (B) 4 (C) 5 (D) 10
解:
A
B
C
D
P
得
又
得
①
②
①②式相加得
D
10.
例5. 已知点 O, N, P 在△ABC 所在平面内, 且
则点 O, N, P 依次是△ABC 的 ( )
(A) 重心、外心、垂心 (B) 重心、外心、内心
(C) 外心、重心、垂心 (D) 外心、重心、内心
分析:
如图:
A
B
C
O
△ABC 的外心.
到三角形三顶点的距离相等
的点是
例5. 已知点 O, N, P 在△ABC 所在平面内, 且
则点 O, N, P 依次是△ABC 的 ( )
(A) 重心、外心、垂心 (B) 重心、外心、内心
(C) 外心、重心、垂心 (D) 外心、重心、内心
分析:
A
B
C
N
D
三角形的重心到顶点的距离等于到对边中点距离
向量.
的两倍,
所以 N 是△ABC 的重心.
即以 与 是相反
即图中
例5. 已知点 O, N, P 在△ABC 所在平面内, 且
则点 O, N, P 依次是△ABC 的 ( )
(A) 重心、外心、垂心 (B) 重心、外心、内心
(C) 外心、重心、垂心 (D) 外心、重心、内心
分析:
A
B
C
P
即
得 PB⊥AC, PC⊥AB.
∴P 是△ABC 的垂心.
C
移项提取公因式得
复习参考题
习题解答
返回目录
1 .判断题:
(1)
(4)
(3)
(2)
0
0
A组
(1) 如果 a, b 是两个单位向量,那么下列四个结
论中正确的是 ( ).
( A ) a=b ( B )a·b=1
( C ) a2≠b2 ( D )|a|2=|b|2
D
2. 选择题:
(2) 对于任意向量a、b, 下列命题中正确的是( ).
(A) 若a、b满足|a|>|b|, 且a与b同向, 则a>b
(B) |a+b|≤|a|+|b|
(C) |a·b|≥|a| |b|
(D) |a-b|≤|a|-|b|
向量不能比较大小.
当 同向时取等号,
≤
B
(3) 在四边形ABCD中, 若 则 ( ).
(A) ABCD是矩形 (B) ABCD是菱形
(C) ABCD是正方形 (D) ABCD是平行四边形
(4) 设 a 是非零向量, l 是非零实数, 下列结论中正
确的是 ( ).
(A) a 与 -l a 方向相反 (B) |-l a|≥|a|
(C) a 与 l2a 的方向相同 (D) |-l a| = |l|·a
加法的平行四边形法则:
A
B
C
D
D
C
(5) 设M是□ABCD的对角线的交点, O为任意一点,
则 等于 ( ).
(A) (B)
(C) (D)
M
A
B
C
D
O
分析:
如图,
分别取AB、CD的中点E、F,
D
E
F
(6) 下列各组向量中, 可以作为基底的是 ( ).
(A) e1=(0, 0), e2=(1, -2)
(B) e1=(-1, 2), e2=(5, 7)
(C) e1=(3, 5), e2=(6, 10)
(D) e1=(2, -3), e2=( )
基底非零, 不共线.
B
解:
A
B
C
D
O
如图,
3. 已知 且 =a, =b, 分别用a、b表示
A
B
C
D
E
F
解:
4. 已知六边形ABCDEF 为正六边形, 且 =a,
=b, 分别用a、b表示
M
设 AC 交 BD 于 M,
由 △BMC∽△DMA,
且 AD=2BC 得
A
B
C
D
E
F
解:
4. 已知六边形ABCDEF 为正六边形, 且 =a,
=b, 分别用a、b表示
M
设 AC 交 BD 于 M,
由 △BMC∽△DMA,
且 AD=2BC 得
解: (1)
= (8, -8);
(2)
=(-3+5, -4 -12)
= (2, -16);
=(-3-5, -4 +12)
= (-8, 8 ).
(3)
= -3?5+(-4)×(-12)
= 33.
5. 已知平面直角坐标系中, 点 O 为原点, A(-3, -4 )、B( 5, -12 ).
(1) 求 的坐标及
(2) 若 求 及 的坐标;
(3) 求
6. 已知点A(0, 1), B(1, 0), C(1, 2), D(2, 1), 试判断向量 和 的位置关系, 并给以证明.
解:
x
y
o
A
2
B
2
C
D
如图知,
证明:
7.已知点A ( 1 , 1)、B (-1, 0 )、C (0, 1).求点D(x, y), 使
解:
= (-2, -1),
∴点D的坐标为(-2, 0).
解得
8. n 为何值时, 向量 a=(n, 1)与 b=(4, n)共线且方向相同?
解:
解得 n=2,
答: n=2时, 与 共线且方向相同.
9. 已知a=(1, 0), b=(1, 1), c=(-1, 0), 求l 和 m, 使 c=la+mb.
解:
= l(1, 0) + m(1, 1 )
= ( l+m, m ),
10. 已知△ABC的顶点坐标分别为A(1, 1), B(4, 1), C(4, 5), 求cosA, cosB, cosC的值
解:
由题设得
= 0.6;
= 0;
= 0.8.
11. 已知单位向量 m 和 n 的夹角为60?, 求证: (2n-m)⊥m, 并解释其几何意义.
证明:
= 0,
A
B
C
其几何意义如图:
∠BAC=60?,
是一直角三角形的三边长.
12. 已知 a = (1 , 0 ), b = (1 , 1 ) ,当l为何值时, a+lb 与 a 垂直?
解:
解得 l = -1.
13. 已知|a | = |b|= 2 , a 与b 的夹角为30? , 求 |a+b|, |a -b| .
解:
= 1.
14. 如图, 支座 A 受 F1、F2 两个力的作用, 已知|F1|=40 N, 与水平线成q 角; |F2|=70 N, 沿水平方向; 两个力的合力 |F |=100 N, 求角q 以及合力F 与水平线的夹角b.
A
B
C
D
F1
F2
F
b
q
解:
|F| = |F1+F2|
=100,
解得cosq =
|F1| = |F-F2|
=40,
解得cosb =
B组
1. 选择题:
(1) 已知 =a+5b, = -2a+8b, =3(a-b), 则 ( ).
(A) A、B、D三点共线 (B) A、B、C三点共线
(C) B、C、D三点共线 (D) A、C、D三点共线
分析:
考查
A、B、C不共线;
同理B、C、D不共线;
∴A、B、D三点共线.
A
(2) 已知正方形ABCD的边长为1, =a, =b,
=c, 则 |a+b+c| 等于 ( ).
(A) 0 (B) 3 (C) (D)
A
C
B
D
解:
如图,
D
(3) 已知 =a, =b, =c, =d, 且四边形ABCD为平行四边形, 则 ( ).
(A) a+b+c+d=0 (B) a-b+c-d=0
(C) a+b-c-d=0 (D) a-b-c+d=0
M
A
B
C
D
O
E
F
分析:
如图,
B
(4) 已知D、E、F分别是△ABC的边BC、CA、AB
的中点, 且 =a, =b, =c, 则 ①
② ③ ④
中正确的等式的个数为 ( )
(A) 1 (B) 2 (C) 3 (D)4
分析:
A
B
C
D
E
F
C
(5) 若 e1, e2 是夹角为60?的两个单位向量, 则a=2e1+e2; b = -3e1+2e2 的夹角为 ( ).
(A) 30? (B) 60? (C) 120? (D) 150?
解:
= 7,
q =120?.
C
(6) 若向量 a、b、c 两两所成的角相等, 且| a |=1, | b |=1, | c |=3, 则 |a+b+c| 等于 ( ).
(A) 2 (B) 5 (C) 2或5 (D)
解:
不同向时, 两两的夹角为120?,
= 2.
三向量同向时, 夹角为0?,
= 5;
C
(7) 等边三角形ABC的边长为 1, =a, =b,
=c, 那么 a·b+b·c+c·a 等于 ( ).
(A) 3 (B) -3 (C) (D)
A
B
C
解:
3cos120?
D
2 .已知向量 a 、b 为非零向量,求证:a ⊥b ? |a + b | = |a -b | , 并解释其几何意义.
证明:
几何意义:
矩形的两条对角线相等.
3 .已知a + b = c,a - b = d , 求证:| a | = | b | ? c⊥d, 并解释其几何意义 .
证明:
反之,
几何意义:
菱形的对角
线互相垂直.
4. 如图, 已知四边形ABCD是等腰梯形, E、F分别是腰AD、BC的中点, M、N是线段EF上的两个点, 且EM = MN = NF, 下底是上底的 2 倍, 若 =a, =b, 求
·
·
A
B
C
D
E
F
M
N
解:
证明:
5. 已知向量 满足条
求证: △P1P2P3是正三角形.
P1
P2
P3
O
E
如图,
则P1、O、E共线, 且是P2P3边的中线,
?OE⊥P2P3,
?|P1P2| = |P1P3|,
F
又
则∠OP2F=60?,
?∠OP2P3=30?,
?∠P1P2P3=60?,
∴△P1P2P3是正三角形.
证明:
同理得
同理得
即△P1P2P3是正三角形.
5. 已知向量 满足条
求证: △P1P2P3是正三角形.
(法二: 代数法)
6. 如图, 已知 =a, =b, 任意点M关于点A的对称点为S, 点S关于点B的对称点为N, 用a、b表示向量
x
o
y
S
M
N
A
B
解:
中位线,
由对称知AB是△SMN的
6. 如图, 已知 =a, =b, 任意点M关于点A的对称点为S, 点S关于点B的对称点为N, 用a、b表示向量
x
o
y
S
M
N
A
B
解:
(解析法)
设M(x1, y1), N(x2, y2), S(x3, y3),
A(a1, b1), B(a2, b2).
由中点坐标得:
2a1=x1+x3,
2b1=y1+y3,
2a2=x2+x3,
2b2=y2+y3,
①
②
③
④
③ - ① ?x2-x1=2a2-2a1,
④ - ② ?y2-y1=2b2-2b1,
7. 某人在静水中游泳, 速度为 千米/时, 他在水流速度为4千米/时的河中游泳.
(1) 如果他垂直游向河对岸, 那么他实际沿什么方向前进? 实际前进的速度为多少?
(2) 他必须朝哪个方向游, 才能沿与水流垂直的方向前进? 实际前进的速度为多少?
A
B
C
D
解:
(1)
为游速,
为水流速,
为实际游速,
tan∠DAC=
∠DAC= 60?.
= 8,
答: 实际与水流成60?的角前进, 速度为8千米/时.
7. 某人在静水中游泳, 速度为 千米/时, 他在水流速度为4千米/时的河中游泳.
(1) 如果他垂直游向河对岸, 那么他实际沿什么方向前进? 实际前进的速度为多少?
(2) 他必须朝哪个方向游, 才能沿与水流垂直的方向前进? 实际前进的速度为多少?
解:
(2)
A
B
C
D
tan∠BAD=
∠BAD= 30?,
答: 与水流方向成120?的角时, 实际游向垂直
水流, 实际前进速度为 千米/时.
8. 在△ABC中, 若 那么点O在△ABC的什么位置?
A
B
C
O
解:
由
即
同理, 由
∴点O是△ABC的垂心, 位于三条高的交点.
9. 平面直角坐标系内的向量都可以用一有序实数对唯一表示, 这使我们想到可以用向量作为解析几何的研究工具. 如图, 设直线 l 的倾斜角为a (a≠90?). 在 l 上任取两个不同的点P1(x1, y1), P2(x2, y2), 不妨设向量 的方向是向上的, 那么向量 的坐标是(x2-x1, y2-y1). 过原点作向量 则点P的坐标是(x2-x1, y2-y1), 而且直线OP的倾斜角也是a. 根据正切函数的定义得
这是《数学2》中已经得到的斜率
公式. 上述推导过程比《数学2》
中的推导简捷.
x
o
y
a
P
P1
P2
a
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(1) 过点P0(x0, y0), 平行于向量a=(a1, a2)的直线方程;
(2) 向量(A, B)与直线Ax+By+C=0的关系;
(3) 设直线l1和l2的方程分别是
l1: A1x+B1y+C1=0,
l2: A2x+B2y+C2=0,
那么, l1//l2, l1⊥l2的条件各是什么? 如果它们相交, 如何得到它们的夹角公式?
(4) 点P0(x0, y0)到直线Ax+By+C=0的距离公式如何推导?
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(1) 过点P0(x0, y0), 平行于向量a=(a1, a2)的直线方程;
分析:
所求直线上的任一点P与P0点构成的向量与
即可用向量共线的关系建立方程.
共线,
解:
设所求直线上任一点P(x, y),
则向量 与 共线,
得 a2(x-x0)-a1(y-y0)=0,
整理得 a2x-a1y-a2x0+a1y0=0.
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(2) 向量(A, B)与直线Ax+By+C=0的关系;
分析:
考虑关系, 即平行、相交、或垂直.
可在直线上取一向量考虑.
解:
在直线上取两点P1(0, ),
P2( 0),
向量
∴向量(A, B)与直线Ax+By+C=0不平行,
-C+C=0,
则向量(A, B)垂直于直线Ax+By+C=0.
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(2) 向量(A, B)与直线Ax+By+C=0的关系;
分析:
考虑关系, 即平行、相交、或垂直.
可在直线上取一向量考虑.
解:
在直线上取两点P1(0, ),
P2( 0),
向量
是直线的斜率 k,
∴把(1, k)叫直线 y=kx+b的一个方向向量,
则 的一个方向向量是
∴向量(A, B) 与直线垂直.
(又解)
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(3) 设直线l1和l2的方程分别是
l1: A1x+B1y+C1=0,
l2: A2x+B2y+C2=0,
那么, l1//l2, l1⊥l2的条件各是什么? 如果它们相交, 如何得到它们的夹角公式?
解:
取l1、l2的方向向量分别为
若
即 A1B2-A2B1= 0时, l1//l2.
若
即 A1A2+B1B2= 0时, l1⊥l2.
①
若 B1=B2= 0时, ①式也成立.
若 B1=A2= 0,
或 B2=A1= 0时,
②式也成立.
②
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(3) 设直线l1和l2的方程分别是
l1: A1x+B1y+C1=0,
l2: A2x+B2y+C2=0,
那么, l1//l2, l1⊥l2的条件各是什么? 如果它们相交, 如何得到它们的夹角公式?
解:
取l1、l2的方向向量分别为
设 l1、l2的夹角为q (非钝角),
则
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(4) 点P0(x0, y0)到直线Ax+By+C=0的距离公式如何推导?
分析:
如图,
构造一个Rt△P0AP,
·
P0
l
P
A
|P0A| 即为所求的点线距离,
q
|P0A| =
即
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(4) 点P0(x0, y0)到直线Ax+By+C=0的距离公式如何推导?
解:
设直线 l: Ax+By+C=0,
在l上取一点P(0, ),
·
P0
l
P
A
取P0A的一个方向向量为
q
得
则
自我检测题
返回目录
自我检测题
一、选择题
1. 在平行四边形ABCD中, 则下列运算正确的是 ( )
(A) a+b-c+d=0 (B) a-b+c-d=0 (C) a+b-c-d=0 (D) a-b-c+d=0
2. 下面给出的关系式中正确的个数是 ( )
① 0·a=0; ② a·b=b·a; ③ a2=|a|2; ④ (a·b)·c=a·(b·c); ⑤ |a·b|≤a·b.
(A) 0 (B) 1 (C) 2 (D) 3
3. 对于非零向量a, b, 下列命题中正确的是 ( )
(A) a· b=0?a=0或b=0 (B) a//b?a在b上的投影为|a|
(C) a⊥b?a·b=(a·b)2 (D) a·c=b·c?a=b
4. 已知a=(5, -2), b=(-4, -3), c=(x, y), 若a-2b+3c=0, 则c等于( )
(A) (B) (C) (D)
5. 若 则 l 的值为 ( )
(A) (B) (C) (D)
6. 已知△ABC的三个顶点A、B、C及平面内一点P, 若 则点P与△ABC的位置
关系是 ( )
(A) P在AC边上 (B) P在AB边上或其延长线上 (C) P在△ABC外部 (D) P在△ABC内部
二、填空题
1. 若a=(6, -8), 则与a平行的单位向量是 .
2. 已知向量|a|=3, b=(1, 2). 且a⊥b, 则 a 的坐标是 .
3. 设e1, e2为两个不共线的向量, 若a=e1+le2与 b=-(2e1-3e2)共线, 则l= .
4. 若|a|=1, |b|= (a-b)·a=0, 则 a 与 b 的夹角为 .
三、解答题
1. 已知向量a=3e1-2e2, b=4e1+e2, 其中e1=(1, 0), e2=(0, 1). 求:
(1) a·b; |a+b|; (2) a与b的夹角的余弦值.
2. 如图, 求点B与点C的坐标.
x
y
O
A
B
C
A
B
C
D
O
一、选择题
1. 在平行四边形ABCD中,
则下列运算正确的是 ( )
(A) a+b-c+d=0 (B) a-b+c-d=0
(C) a+b-c-d=0 (D) a-b-c+d=0
A
B
C
D
O
解:
如图,
B
(A)
(A) 错.
(B)
(B) 对.
2. 下面给出的关系式中正确的个数是 ( )
① 0·a=0; ② a·b=b·a; ③ a2=|a|2; ④ (a·b)·c=a·(b·c); ⑤ |a·b|≤a·b.
(A) 0 (B) 1 (C) 2 (D) 3
夹角为钝角时, ⑤就不成立.
D
3. 对于非零向量 a, b, 下列命题中正确的是 ( )
(A) a·b=0?a=0 或 b=0
(B) a//b?a 在 b 上的投影为 |a|
(C) a⊥b?a·b=(a·b)2
(D) a·c=b·c?a=b
(A) 错,
有可能
(B) 错,
反向时, 投影为
(C) 对,
C
4. 已知 a=(5. -2), b=(-4, -3), c=(x, y), 若 a-2b+3c=0, 则 c 等于 ( )
(A) (B) (C) (D)
解:
=(13+3x, 4+3y)
=0,
则 13+3x=0,
4+3y=0,
D
5. 若 则 l 的值为 ( )
(A) (B) (C) (D)
解:
D
6. 已知△ABC 的三个顶点 A、B、C 及平面内一点 P, 若 则点 P 与△ABC 的位置关系是 ( )
(A) P 在 AC 边上
(B) P 在 AB 边上或其延长线上
(C) P 在△ABC 外部
(D) P 在△ABC 内部
得
解:
与 共线, 且方向相反.
∴ P 点在 AC 边上.
A
二、填空题
1. 若 a=(6, -8), 则与 a 平行的单位向量是 .
解:
设所求向量为
则 (6l)2+(-8l)2=1,
得
(0.6, -0.8)
(-0.6, 0.8)
2. 已知向量 |a|=3, b=(1, 2), 且 a⊥b, 则 a 的坐标是 .
解:
设
则
x+2y=0,
解得
或
3. 设 e1, e2 为两个不共线的向量, 若 a=e1+le2 与 b= -(2e1-3e2) 共线, 则 l= .
解:
与 共线, 设
即
得
解得
4. 若 |a|=1, |b|= (a-b)·a=0, 则 a 与 b 的夹角为 .
解:
q =45?.
45?
三、解答题
1. 已知向量 a=3e1-2e2, b=4e1+e2, 其中 e1=(1, 0), e2=(0, 1). 求:
(1) a·b; |a+b|;
(2) a 与 b 的夹角的余弦值.
解:
(1)
=(3, -2).
=(4, 1).
=10.
(2)
2. 如图,
求点 B 与点 C 的坐标.
x
y
O
A
B
C
解:
设 B(x, y),
①
②
由①②解得
∴ 点 B 的坐标为
由题设得
则
2. 如图,
求点 B 与点 C 的坐标.
x
y
O
A
B
C
解:
设 C(x, y),
①
②
则
由点 B 的坐标得
由①②解得
2. 如图,
求点 B 与点 C 的坐标.
x
y
O
A
B
C
解:
法二, 几何法:
D
G
作 BD⊥x 轴于 D,
CG//y 轴, 交 BG 于G, (如图)
作 BG//x 轴,
在 Rt△BAD中, AB=a, ∠BAD=60?.
则
于是得点 B 的坐标为
在 Rt△CBG中, BC=2a, ∠CBG=60?.
则
于是得点 C 的坐标为
平面向量
本章内容
2.1 平面向量的实际背景及基本概念
2.2 平面向量的线性运算
2.3 平面向量的基本定理及坐标表示
2.4 平面向量的数量积
2.5 平面向量应用举例
第二章 小结
本章小结
本章小结
知识要点
例题选讲
复习参考题
自我检测题
知识要点
1. 向量的基本概念
返回目录
向量用有向线段表示.
② 用印刷黑体小写字母表示, 如 a、b、c.
① 用端点的大写字母表示, 如
③ 用书写体加箭头表示, 如
字母表示有三种方法:
向量的大小叫做向量的模,
A
B
3
如:
用有向线段的长度表示,
知识要点
1. 向量的基本概念
◆模为零的向量称为零向量.
◆模为一个单位的向量称为单位向量.
零向量记作 0 ( ).
零向量的方向是任意的.
◆长度相等, 方向相同的向量叫做相等向量.
知识要点
2. 向量加减法
(1) 几何运算
加法的平行四边形法则、三角形法则.
减法的三角形法则 (同起点向量相减).
(2) 代数运算
知识要点
3. 向量的数乘
l>0 时,
与 同向.
l<0 时,
与 反向.
(l?R) 表示 l 个 相加.
知识要点
4. 共线向量
一组平行向量称为共线向量.
共线向量的方向相同或相反.
若 A、B、C 三点共线, 则
(l+m =1).
知识要点
5. 向量基本定理
不共线 (基底),
任一向量
(l, m?R).
知识要点
6. 向量的坐标表示
为 x 轴, y 轴方向的单位向量,
A(x1, y1), B(x2, y2),
O(0, 0), P(x, y),
知识要点
7. 向量的数量积
=OC·OB
=OD·OA.
q
D
O
C
A
B
正投影
正投影
几何意义:
知识要点
8. 数量积的运算定律
(1) a·b=b·a:
(2) (la)·b=l(a·b)=a·(lb) (l为实数);
(3) (a+b)·c=a·c+b·c;
(4) a2=|a|2.
(a·b)·c≠a·(b·c).
知识要点
9. 向量共线与垂直
a⊥b ?? x1x2+y1y2=0.
a//b ?? b=la(l?R).
a//b ?? x1y2-x2y1=0
知识要点
10. 分点与距离
P(x, y), P1(x1, y1), P2(x2, y2),
P 为中点:
例1. 求证: 直径上的圆周角为直角.
例题选讲
O
·
A
B
C
如图, 已知 AB 是⊙O 的直径, C 是圆上的点. 求证: ∠ACB 为直角.
分析:
目标:
证
向量运算结果为 0 的有
思考将 用向量加减法转换到 上来.
返回目录
例1. 求证: 直径上的圆周角为直角.
例题选讲
O
·
A
B
C
如图, 已知 AB 是⊙O 的直径, C 是圆上的点. 求证: ∠ACB 为直角.
证明:
即
∴∠ACB 是直角.
提取公因式
相反向量
例2. 如图, AD、BE、CF 是△ABC 的三条高. 求证: AD、BE、CF 相交于一点.
A
B
C
D
E
F
思路:
(1) 先定两条高交于一点,
如 BE 与 CF 交于点 H.
(2) 如果 AH⊥BC, 即得三条
高共点.
H
目标:
方法:
将 和 用互相垂直的向量运算代替.
例2. 如图, AD、BE、CF 是△ABC 的三条高. 求证: AD、BE、CF 相交于一点.
A
B
C
D
E
F
证明:
设 BE 与 CF 交于点 H.
H
∵CF⊥AB, BE⊥AC,
=0.
得 AH⊥BC,
∴三条高交于一点.
例3. 如图, 在平行四边形 ABCD 中, AP⊥BD,垂足为 P, 且 AP=3, 则
A
B
C
D
P
分析:
题设中除了一个垂直
关系外, 只有一个已知量,
所求问题需向着已知量转化.
根据垂直关系以及向量数量积的几何意义,
思考已知量 AP 是哪些向量的正投影.
于是可找到
问题就变为将 转化到
例3. 如图, 在平行四边形 ABCD 中, AP⊥BD,垂足为 P, 且 AP=3, 则
A
B
C
D
P
解:
∵AP⊥BD,
=18.
18
例4. 在直角三角形 ABC 中, 点 D 是斜边 AB 的
中点, 点 P 为线段 CD 的中点, 则
(A) 2 (B) 4 (C) 5 (D) 10
分析:
(1) PA, PB, PC 有什么关系?
如图,
A
B
C
D
P
将上式平方有可能达到目标.
(2) 另一运算
平方上式也可能达到目标.
由这两条路切入一试.
例4. 在直角三角形 ABC 中, 点 D 是斜边 AB 的
中点, 点 P 为线段 CD 的中点, 则
(A) 2 (B) 4 (C) 5 (D) 10
解:
A
B
C
D
P
得
又
得
①
②
①②式相加得
D
10.
例5. 已知点 O, N, P 在△ABC 所在平面内, 且
则点 O, N, P 依次是△ABC 的 ( )
(A) 重心、外心、垂心 (B) 重心、外心、内心
(C) 外心、重心、垂心 (D) 外心、重心、内心
分析:
如图:
A
B
C
O
△ABC 的外心.
到三角形三顶点的距离相等
的点是
例5. 已知点 O, N, P 在△ABC 所在平面内, 且
则点 O, N, P 依次是△ABC 的 ( )
(A) 重心、外心、垂心 (B) 重心、外心、内心
(C) 外心、重心、垂心 (D) 外心、重心、内心
分析:
A
B
C
N
D
三角形的重心到顶点的距离等于到对边中点距离
向量.
的两倍,
所以 N 是△ABC 的重心.
即以 与 是相反
即图中
例5. 已知点 O, N, P 在△ABC 所在平面内, 且
则点 O, N, P 依次是△ABC 的 ( )
(A) 重心、外心、垂心 (B) 重心、外心、内心
(C) 外心、重心、垂心 (D) 外心、重心、内心
分析:
A
B
C
P
即
得 PB⊥AC, PC⊥AB.
∴P 是△ABC 的垂心.
C
移项提取公因式得
复习参考题
习题解答
返回目录
1 .判断题:
(1)
(4)
(3)
(2)
0
0
A组
(1) 如果 a, b 是两个单位向量,那么下列四个结
论中正确的是 ( ).
( A ) a=b ( B )a·b=1
( C ) a2≠b2 ( D )|a|2=|b|2
D
2. 选择题:
(2) 对于任意向量a、b, 下列命题中正确的是( ).
(A) 若a、b满足|a|>|b|, 且a与b同向, 则a>b
(B) |a+b|≤|a|+|b|
(C) |a·b|≥|a| |b|
(D) |a-b|≤|a|-|b|
向量不能比较大小.
当 同向时取等号,
≤
B
(3) 在四边形ABCD中, 若 则 ( ).
(A) ABCD是矩形 (B) ABCD是菱形
(C) ABCD是正方形 (D) ABCD是平行四边形
(4) 设 a 是非零向量, l 是非零实数, 下列结论中正
确的是 ( ).
(A) a 与 -l a 方向相反 (B) |-l a|≥|a|
(C) a 与 l2a 的方向相同 (D) |-l a| = |l|·a
加法的平行四边形法则:
A
B
C
D
D
C
(5) 设M是□ABCD的对角线的交点, O为任意一点,
则 等于 ( ).
(A) (B)
(C) (D)
M
A
B
C
D
O
分析:
如图,
分别取AB、CD的中点E、F,
D
E
F
(6) 下列各组向量中, 可以作为基底的是 ( ).
(A) e1=(0, 0), e2=(1, -2)
(B) e1=(-1, 2), e2=(5, 7)
(C) e1=(3, 5), e2=(6, 10)
(D) e1=(2, -3), e2=( )
基底非零, 不共线.
B
解:
A
B
C
D
O
如图,
3. 已知 且 =a, =b, 分别用a、b表示
A
B
C
D
E
F
解:
4. 已知六边形ABCDEF 为正六边形, 且 =a,
=b, 分别用a、b表示
M
设 AC 交 BD 于 M,
由 △BMC∽△DMA,
且 AD=2BC 得
A
B
C
D
E
F
解:
4. 已知六边形ABCDEF 为正六边形, 且 =a,
=b, 分别用a、b表示
M
设 AC 交 BD 于 M,
由 △BMC∽△DMA,
且 AD=2BC 得
解: (1)
= (8, -8);
(2)
=(-3+5, -4 -12)
= (2, -16);
=(-3-5, -4 +12)
= (-8, 8 ).
(3)
= -3?5+(-4)×(-12)
= 33.
5. 已知平面直角坐标系中, 点 O 为原点, A(-3, -4 )、B( 5, -12 ).
(1) 求 的坐标及
(2) 若 求 及 的坐标;
(3) 求
6. 已知点A(0, 1), B(1, 0), C(1, 2), D(2, 1), 试判断向量 和 的位置关系, 并给以证明.
解:
x
y
o
A
2
B
2
C
D
如图知,
证明:
7.已知点A ( 1 , 1)、B (-1, 0 )、C (0, 1).求点D(x, y), 使
解:
= (-2, -1),
∴点D的坐标为(-2, 0).
解得
8. n 为何值时, 向量 a=(n, 1)与 b=(4, n)共线且方向相同?
解:
解得 n=2,
答: n=2时, 与 共线且方向相同.
9. 已知a=(1, 0), b=(1, 1), c=(-1, 0), 求l 和 m, 使 c=la+mb.
解:
= l(1, 0) + m(1, 1 )
= ( l+m, m ),
10. 已知△ABC的顶点坐标分别为A(1, 1), B(4, 1), C(4, 5), 求cosA, cosB, cosC的值
解:
由题设得
= 0.6;
= 0;
= 0.8.
11. 已知单位向量 m 和 n 的夹角为60?, 求证: (2n-m)⊥m, 并解释其几何意义.
证明:
= 0,
A
B
C
其几何意义如图:
∠BAC=60?,
是一直角三角形的三边长.
12. 已知 a = (1 , 0 ), b = (1 , 1 ) ,当l为何值时, a+lb 与 a 垂直?
解:
解得 l = -1.
13. 已知|a | = |b|= 2 , a 与b 的夹角为30? , 求 |a+b|, |a -b| .
解:
= 1.
14. 如图, 支座 A 受 F1、F2 两个力的作用, 已知|F1|=40 N, 与水平线成q 角; |F2|=70 N, 沿水平方向; 两个力的合力 |F |=100 N, 求角q 以及合力F 与水平线的夹角b.
A
B
C
D
F1
F2
F
b
q
解:
|F| = |F1+F2|
=100,
解得cosq =
|F1| = |F-F2|
=40,
解得cosb =
B组
1. 选择题:
(1) 已知 =a+5b, = -2a+8b, =3(a-b), 则 ( ).
(A) A、B、D三点共线 (B) A、B、C三点共线
(C) B、C、D三点共线 (D) A、C、D三点共线
分析:
考查
A、B、C不共线;
同理B、C、D不共线;
∴A、B、D三点共线.
A
(2) 已知正方形ABCD的边长为1, =a, =b,
=c, 则 |a+b+c| 等于 ( ).
(A) 0 (B) 3 (C) (D)
A
C
B
D
解:
如图,
D
(3) 已知 =a, =b, =c, =d, 且四边形ABCD为平行四边形, 则 ( ).
(A) a+b+c+d=0 (B) a-b+c-d=0
(C) a+b-c-d=0 (D) a-b-c+d=0
M
A
B
C
D
O
E
F
分析:
如图,
B
(4) 已知D、E、F分别是△ABC的边BC、CA、AB
的中点, 且 =a, =b, =c, 则 ①
② ③ ④
中正确的等式的个数为 ( )
(A) 1 (B) 2 (C) 3 (D)4
分析:
A
B
C
D
E
F
C
(5) 若 e1, e2 是夹角为60?的两个单位向量, 则a=2e1+e2; b = -3e1+2e2 的夹角为 ( ).
(A) 30? (B) 60? (C) 120? (D) 150?
解:
= 7,
q =120?.
C
(6) 若向量 a、b、c 两两所成的角相等, 且| a |=1, | b |=1, | c |=3, 则 |a+b+c| 等于 ( ).
(A) 2 (B) 5 (C) 2或5 (D)
解:
不同向时, 两两的夹角为120?,
= 2.
三向量同向时, 夹角为0?,
= 5;
C
(7) 等边三角形ABC的边长为 1, =a, =b,
=c, 那么 a·b+b·c+c·a 等于 ( ).
(A) 3 (B) -3 (C) (D)
A
B
C
解:
3cos120?
D
2 .已知向量 a 、b 为非零向量,求证:a ⊥b ? |a + b | = |a -b | , 并解释其几何意义.
证明:
几何意义:
矩形的两条对角线相等.
3 .已知a + b = c,a - b = d , 求证:| a | = | b | ? c⊥d, 并解释其几何意义 .
证明:
反之,
几何意义:
菱形的对角
线互相垂直.
4. 如图, 已知四边形ABCD是等腰梯形, E、F分别是腰AD、BC的中点, M、N是线段EF上的两个点, 且EM = MN = NF, 下底是上底的 2 倍, 若 =a, =b, 求
·
·
A
B
C
D
E
F
M
N
解:
证明:
5. 已知向量 满足条
求证: △P1P2P3是正三角形.
P1
P2
P3
O
E
如图,
则P1、O、E共线, 且是P2P3边的中线,
?OE⊥P2P3,
?|P1P2| = |P1P3|,
F
又
则∠OP2F=60?,
?∠OP2P3=30?,
?∠P1P2P3=60?,
∴△P1P2P3是正三角形.
证明:
同理得
同理得
即△P1P2P3是正三角形.
5. 已知向量 满足条
求证: △P1P2P3是正三角形.
(法二: 代数法)
6. 如图, 已知 =a, =b, 任意点M关于点A的对称点为S, 点S关于点B的对称点为N, 用a、b表示向量
x
o
y
S
M
N
A
B
解:
中位线,
由对称知AB是△SMN的
6. 如图, 已知 =a, =b, 任意点M关于点A的对称点为S, 点S关于点B的对称点为N, 用a、b表示向量
x
o
y
S
M
N
A
B
解:
(解析法)
设M(x1, y1), N(x2, y2), S(x3, y3),
A(a1, b1), B(a2, b2).
由中点坐标得:
2a1=x1+x3,
2b1=y1+y3,
2a2=x2+x3,
2b2=y2+y3,
①
②
③
④
③ - ① ?x2-x1=2a2-2a1,
④ - ② ?y2-y1=2b2-2b1,
7. 某人在静水中游泳, 速度为 千米/时, 他在水流速度为4千米/时的河中游泳.
(1) 如果他垂直游向河对岸, 那么他实际沿什么方向前进? 实际前进的速度为多少?
(2) 他必须朝哪个方向游, 才能沿与水流垂直的方向前进? 实际前进的速度为多少?
A
B
C
D
解:
(1)
为游速,
为水流速,
为实际游速,
tan∠DAC=
∠DAC= 60?.
= 8,
答: 实际与水流成60?的角前进, 速度为8千米/时.
7. 某人在静水中游泳, 速度为 千米/时, 他在水流速度为4千米/时的河中游泳.
(1) 如果他垂直游向河对岸, 那么他实际沿什么方向前进? 实际前进的速度为多少?
(2) 他必须朝哪个方向游, 才能沿与水流垂直的方向前进? 实际前进的速度为多少?
解:
(2)
A
B
C
D
tan∠BAD=
∠BAD= 30?,
答: 与水流方向成120?的角时, 实际游向垂直
水流, 实际前进速度为 千米/时.
8. 在△ABC中, 若 那么点O在△ABC的什么位置?
A
B
C
O
解:
由
即
同理, 由
∴点O是△ABC的垂心, 位于三条高的交点.
9. 平面直角坐标系内的向量都可以用一有序实数对唯一表示, 这使我们想到可以用向量作为解析几何的研究工具. 如图, 设直线 l 的倾斜角为a (a≠90?). 在 l 上任取两个不同的点P1(x1, y1), P2(x2, y2), 不妨设向量 的方向是向上的, 那么向量 的坐标是(x2-x1, y2-y1). 过原点作向量 则点P的坐标是(x2-x1, y2-y1), 而且直线OP的倾斜角也是a. 根据正切函数的定义得
这是《数学2》中已经得到的斜率
公式. 上述推导过程比《数学2》
中的推导简捷.
x
o
y
a
P
P1
P2
a
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(1) 过点P0(x0, y0), 平行于向量a=(a1, a2)的直线方程;
(2) 向量(A, B)与直线Ax+By+C=0的关系;
(3) 设直线l1和l2的方程分别是
l1: A1x+B1y+C1=0,
l2: A2x+B2y+C2=0,
那么, l1//l2, l1⊥l2的条件各是什么? 如果它们相交, 如何得到它们的夹角公式?
(4) 点P0(x0, y0)到直线Ax+By+C=0的距离公式如何推导?
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(1) 过点P0(x0, y0), 平行于向量a=(a1, a2)的直线方程;
分析:
所求直线上的任一点P与P0点构成的向量与
即可用向量共线的关系建立方程.
共线,
解:
设所求直线上任一点P(x, y),
则向量 与 共线,
得 a2(x-x0)-a1(y-y0)=0,
整理得 a2x-a1y-a2x0+a1y0=0.
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(2) 向量(A, B)与直线Ax+By+C=0的关系;
分析:
考虑关系, 即平行、相交、或垂直.
可在直线上取一向量考虑.
解:
在直线上取两点P1(0, ),
P2( 0),
向量
∴向量(A, B)与直线Ax+By+C=0不平行,
-C+C=0,
则向量(A, B)垂直于直线Ax+By+C=0.
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(2) 向量(A, B)与直线Ax+By+C=0的关系;
分析:
考虑关系, 即平行、相交、或垂直.
可在直线上取一向量考虑.
解:
在直线上取两点P1(0, ),
P2( 0),
向量
是直线的斜率 k,
∴把(1, k)叫直线 y=kx+b的一个方向向量,
则 的一个方向向量是
∴向量(A, B) 与直线垂直.
(又解)
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(3) 设直线l1和l2的方程分别是
l1: A1x+B1y+C1=0,
l2: A2x+B2y+C2=0,
那么, l1//l2, l1⊥l2的条件各是什么? 如果它们相交, 如何得到它们的夹角公式?
解:
取l1、l2的方向向量分别为
若
即 A1B2-A2B1= 0时, l1//l2.
若
即 A1A2+B1B2= 0时, l1⊥l2.
①
若 B1=B2= 0时, ①式也成立.
若 B1=A2= 0,
或 B2=A1= 0时,
②式也成立.
②
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(3) 设直线l1和l2的方程分别是
l1: A1x+B1y+C1=0,
l2: A2x+B2y+C2=0,
那么, l1//l2, l1⊥l2的条件各是什么? 如果它们相交, 如何得到它们的夹角公式?
解:
取l1、l2的方向向量分别为
设 l1、l2的夹角为q (非钝角),
则
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(4) 点P0(x0, y0)到直线Ax+By+C=0的距离公式如何推导?
分析:
如图,
构造一个Rt△P0AP,
·
P0
l
P
A
|P0A| 即为所求的点线距离,
q
|P0A| =
即
你能用向量作为工具讨论一下直线的有关问题吗? 例如:
(4) 点P0(x0, y0)到直线Ax+By+C=0的距离公式如何推导?
解:
设直线 l: Ax+By+C=0,
在l上取一点P(0, ),
·
P0
l
P
A
取P0A的一个方向向量为
q
得
则
自我检测题
返回目录
自我检测题
一、选择题
1. 在平行四边形ABCD中, 则下列运算正确的是 ( )
(A) a+b-c+d=0 (B) a-b+c-d=0 (C) a+b-c-d=0 (D) a-b-c+d=0
2. 下面给出的关系式中正确的个数是 ( )
① 0·a=0; ② a·b=b·a; ③ a2=|a|2; ④ (a·b)·c=a·(b·c); ⑤ |a·b|≤a·b.
(A) 0 (B) 1 (C) 2 (D) 3
3. 对于非零向量a, b, 下列命题中正确的是 ( )
(A) a· b=0?a=0或b=0 (B) a//b?a在b上的投影为|a|
(C) a⊥b?a·b=(a·b)2 (D) a·c=b·c?a=b
4. 已知a=(5, -2), b=(-4, -3), c=(x, y), 若a-2b+3c=0, 则c等于( )
(A) (B) (C) (D)
5. 若 则 l 的值为 ( )
(A) (B) (C) (D)
6. 已知△ABC的三个顶点A、B、C及平面内一点P, 若 则点P与△ABC的位置
关系是 ( )
(A) P在AC边上 (B) P在AB边上或其延长线上 (C) P在△ABC外部 (D) P在△ABC内部
二、填空题
1. 若a=(6, -8), 则与a平行的单位向量是 .
2. 已知向量|a|=3, b=(1, 2). 且a⊥b, 则 a 的坐标是 .
3. 设e1, e2为两个不共线的向量, 若a=e1+le2与 b=-(2e1-3e2)共线, 则l= .
4. 若|a|=1, |b|= (a-b)·a=0, 则 a 与 b 的夹角为 .
三、解答题
1. 已知向量a=3e1-2e2, b=4e1+e2, 其中e1=(1, 0), e2=(0, 1). 求:
(1) a·b; |a+b|; (2) a与b的夹角的余弦值.
2. 如图, 求点B与点C的坐标.
x
y
O
A
B
C
A
B
C
D
O
一、选择题
1. 在平行四边形ABCD中,
则下列运算正确的是 ( )
(A) a+b-c+d=0 (B) a-b+c-d=0
(C) a+b-c-d=0 (D) a-b-c+d=0
A
B
C
D
O
解:
如图,
B
(A)
(A) 错.
(B)
(B) 对.
2. 下面给出的关系式中正确的个数是 ( )
① 0·a=0; ② a·b=b·a; ③ a2=|a|2; ④ (a·b)·c=a·(b·c); ⑤ |a·b|≤a·b.
(A) 0 (B) 1 (C) 2 (D) 3
夹角为钝角时, ⑤就不成立.
D
3. 对于非零向量 a, b, 下列命题中正确的是 ( )
(A) a·b=0?a=0 或 b=0
(B) a//b?a 在 b 上的投影为 |a|
(C) a⊥b?a·b=(a·b)2
(D) a·c=b·c?a=b
(A) 错,
有可能
(B) 错,
反向时, 投影为
(C) 对,
C
4. 已知 a=(5. -2), b=(-4, -3), c=(x, y), 若 a-2b+3c=0, 则 c 等于 ( )
(A) (B) (C) (D)
解:
=(13+3x, 4+3y)
=0,
则 13+3x=0,
4+3y=0,
D
5. 若 则 l 的值为 ( )
(A) (B) (C) (D)
解:
D
6. 已知△ABC 的三个顶点 A、B、C 及平面内一点 P, 若 则点 P 与△ABC 的位置关系是 ( )
(A) P 在 AC 边上
(B) P 在 AB 边上或其延长线上
(C) P 在△ABC 外部
(D) P 在△ABC 内部
得
解:
与 共线, 且方向相反.
∴ P 点在 AC 边上.
A
二、填空题
1. 若 a=(6, -8), 则与 a 平行的单位向量是 .
解:
设所求向量为
则 (6l)2+(-8l)2=1,
得
(0.6, -0.8)
(-0.6, 0.8)
2. 已知向量 |a|=3, b=(1, 2), 且 a⊥b, 则 a 的坐标是 .
解:
设
则
x+2y=0,
解得
或
3. 设 e1, e2 为两个不共线的向量, 若 a=e1+le2 与 b= -(2e1-3e2) 共线, 则 l= .
解:
与 共线, 设
即
得
解得
4. 若 |a|=1, |b|= (a-b)·a=0, 则 a 与 b 的夹角为 .
解:
q =45?.
45?
三、解答题
1. 已知向量 a=3e1-2e2, b=4e1+e2, 其中 e1=(1, 0), e2=(0, 1). 求:
(1) a·b; |a+b|;
(2) a 与 b 的夹角的余弦值.
解:
(1)
=(3, -2).
=(4, 1).
=10.
(2)
2. 如图,
求点 B 与点 C 的坐标.
x
y
O
A
B
C
解:
设 B(x, y),
①
②
由①②解得
∴ 点 B 的坐标为
由题设得
则
2. 如图,
求点 B 与点 C 的坐标.
x
y
O
A
B
C
解:
设 C(x, y),
①
②
则
由点 B 的坐标得
由①②解得
2. 如图,
求点 B 与点 C 的坐标.
x
y
O
A
B
C
解:
法二, 几何法:
D
G
作 BD⊥x 轴于 D,
CG//y 轴, 交 BG 于G, (如图)
作 BG//x 轴,
在 Rt△BAD中, AB=a, ∠BAD=60?.
则
于是得点 B 的坐标为
在 Rt△CBG中, BC=2a, ∠CBG=60?.
则
于是得点 C 的坐标为
