2020-2021学年高中数学人教A版必修5第二章2.4 等比数列2课时课件(共54张PPT)
文档属性
| 名称 | 2020-2021学年高中数学人教A版必修5第二章2.4 等比数列2课时课件(共54张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 688.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览











文档简介
2.4
等比数列
(第一课时)
第一课时
第二课时
操作题1. 请同学们写出下面数列:
(1) 一种细菌进行分裂繁殖, 1 个细菌一次分裂成 2个, 且每分钟分裂一次, 写出 1 个这种细菌经过 1, 2, 3, 4, …, 分钟后的细菌个数;
(2) 一个容器中盛有10升某种溶液, 每次倒出容器中溶液的一半, 写出每次倒出后容器中剩余溶液数量;
(3) 银行的复利计息方式是: 把前一期的利息加入本金计算下一期的利息. 现存入本金10000元, 年利率为1.98%, 写出 5 年内各年末的本利和.
(1) 2, 4, 8, 16, …
(2) 5,
(3) 10000?1.0198, 10000?1.01982,
10000?1.01983, 10000?1.01984, 10000?1.01985.
问题1. 刚才写出的数列是等差数列吗? 如果不是, 那么它们有什么共同的特征? 根据它们的共同特征你想把它们叫做什么数列?
(1) 2, 4, 8, 16, …
(2) 5,
(3) 10000?1.0198, 10000?1.01982,
10000?1.01983, 10000?1.01984, 10000?1.01985.
特征:
各数列中, 每一项与它前一项的比值是一个相等的数.
(1) 中的比值是 2,
(2) 中的比值是
(3) 中的比值是1.0198.
每一项等于前一项乘以 2.
每一项等于前一项乘以
每一项等于前一项乘以 1.0198.
定义: 一般地, 如果一个数列从第 2 项起, 每一项与它的前一项的比等于同一个常数, 那么这个数列就叫做等比数列, 这个常数叫做等比数列的公比,公比通常用字母 q 表示 (q≠0), 即
则数列 {an} 为等比数列, 常数 q 是公比.
判断几个数是否成等比数列, 看其是否满足
判断以通项表示的数列是否是等比数列, 看其是否满足
(常数).
(4) 不是等比数列,
(2) 是等比数列,
(3) 是等比数列,
问题 2. 下列各数列是否是等比数列? 如果是, 公比是多少?
(1) (2)
(3) 7, 7, 7, 7, … (4) 0, 1, 4, 16, …
(1) 是等比数列, 公比 q =
等比数列的任一项都不能为 0.
a2=a1q,
【等比数列的通项公式】
操作题2. 已知等比数列{an}的首项为 a1, 公比为 q,写出这个数列的 a2, a3, a4, a5, 并由此归纳出 an.
a3=a2q
=a1q2,
a4=a3q
=a1q3,
a5=a4q
=a1q4,
……
猜:an=a1qn-1.
等比数列的通项公式:
an=a1qn-1
等比数列 an=a1qn-1 的图象是函数 y = a1qx-1 的图象上 x 取正整数的点.
等比数列的图像
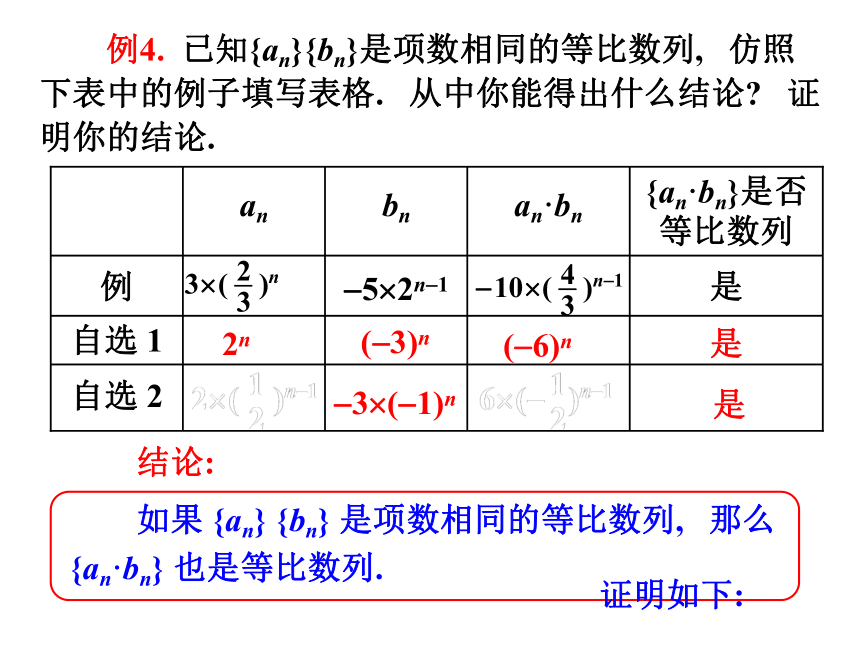
例4. 已知{an}{bn}是项数相同的等比数列, 仿照下表中的例子填写表格. 从中你能得出什么结论? 证明你的结论.
自选 2
自选 1
是
-5?2n-1
例
{an·bn}是否等比数列
an·bn
bn
an
2n
(-3)n
(-6)n
是
-3?(-1)n
是
结论:
如果 {an} {bn} 是项数相同的等比数列, 那么{an·bn} 也是等比数列.
证明如下:
设{an}的公比为 p, {bn}的公比为 q, p, q 为常数,
则
= p·q
(常数),
∴{an·bn}是等比数列.
问题3. 如果{an}是等比数列, c 为常数, 且c≠0,那么{c·an}是否是等比数列, 能证明你的结论吗?
= q (常数).
结论:
一个等比数列的各项都乘以同一个不为 0 的常数,所得的数列仍是等比数列.
问题4. 三个数 2, 3 是否成等比数列? 如果 a, G, b 这三个数成等比数列, G 是多少?
若 a, G, b 成等比数列, 则
? G2=ab,
两比值相等, 三个数成等比数列.
等比中项:
如果在 a 与 b 中间插入一个数 G, 使 a, G, b 成等比数列, 那么 G 叫做 a 与 b 的等比中项,
G2=ab,
等差中项:
如果三个数 a, A, b 成等差数列, 则中间一个数 A 叫做 a 与 b 的等差中项,
或 2A=a+b.
例3. 一个等比数列的第 3 项和第 4 项分别是12和18, 求它的第 1 项与第 2 项.
由等比数列通项公式得,
解:
解关于 a1 与 q 的方程组:
①
②
a3=a1q2=12,
a4=a1q3=18,
②÷① 得
将 q 的值代入①式得
则 a2= a1q
= 8.
∴这个数列的等 1 项是 第 2 项是 8.
练习: (课本53页)
3. 已知{an}是一个无穷等比数列, 公比为 q:
(1) 将{an}中的前 k 项去掉, 剩余各项组成一个新数列, 这个新数列是等比数列吗? 如果是, 它的首项与公比分别是多少?
(2) 取出数列{an}中的所有奇数项, 组成一个新的数列, 这个新数列是等比数列吗? 如果是, 它的首项与公比分别是多少?
(3) 在数列{an}中, 每隔10项取出一项, 组成一个新的数列, 这个新数列是等比数列吗? 如果是, 它的公比是多少? 你能根据得到的结论作出一个猜想吗?
练习: (课本53页)
3. 已知{an}是一个无穷等比数列, 公比为 q:
(1) 将{an}中的前 k 项去掉, 剩余各项组成一个新数列, 这个新数列是等比数列吗? 如果是, 它的首项与公比分别是多少?
答:
其首项是原数列的 ak+1, 公比是原数列的公比 q.
{an} 中去掉前 k 项后分别是
a1+k,
a2+k,
a3+k,
…,
an+k, …
=q,
(常数).
∴{an} 中去掉前 k 项后所得数列是等比数列,
练习: (课本53页)
3. 已知{an}是一个无穷等比数列, 公比为 q:
答:
取出 {an} 中的所有奇数项得
a1, a3, a5, …, a2n-1, …
=q2,
(常数).
∴取出 {an} 中的所有奇数项所得的数列也是等比
数列, 其首项为 a1, 公比为 p2.
(2) 取出数列{an}中的所有奇数项, 组成一个新的数列, 这个新数列是等比数列吗? 如果是, 它的首项与公比分别是多少?
练习: (课本53页)
3. 已知{an}是一个无穷等比数列, 公比为 q:
(3) 在数列{an}中, 每隔10项取出一项, 组成一个新的数列, 这个新数列是等比数列吗? 如果是, 它的公比是多少? 你能根据得到的结论作出一个猜想吗?
答:
在 {an} 中每隔 10 项取出一项得
a11,
=q11,
(常数).
= …
∴ {an} 中每隔 10 项取出一项所得的数列也是等
比数列, 其首项为 a11, 公比为 q11.
a22,
a33,
…,
a10n+n, …
练习: (课本53页)
3. 已知{an}是一个无穷等比数列, 公比为 q:
(3) 在数列{an}中, 每隔10项取出一项, 组成一个新的数列, 这个新数列是等比数列吗? 如果是, 它的公比是多少? 你能根据得到的结论作出一个猜想吗?
猜想:
在等比数列 {an} 中每隔 k 项取出一项,
所得的数列也是等比数列, 其首项为 ak+1, 公比为
qk+1.
【课时小结】
1. 等比数列
一个数列从第 2 项起的每一项与它前一项的比等于同一个常数 q, 则这个数列就叫做等比数列, 常数 q 叫做等比数列的公比, 即
a2=a1·q, a3=a2·q, a4=a3·q, ……, an+1=an·q.
是判定等比数列的条件.
【课时小结】
2. 等比中项
如果在 a 与 b 中间插入一个数 G, 使 a, G, b 成等比数列, 那么 G 叫做 a 与 b 的等比中项, 即
G2=ab.
习题 2.4
A 组
第 3、6、7 题.
习题 2.4
A 组
3. 已知{an}是各项均为正数的等比数列, 是等比数列吗? 为什么?
解:
(常数),
∴ 是等比数列.
6. 已知 a, b 是互异的正数, A 是 a, b 的等差中项, G 是 a, b 的等比中项, A 与 G 有无确定的大小关系?
解:
由题设得
∵a>0, b>0, a≠b,
∴一定有 A>G.
即
得
7. 求下列各组数的等比中项:
(1)
(2) a4+a2b2 与 b4+a2b2 (a≠0, b≠0).
解:
(1)
=±2.
(2)
=±ab(a2+b2).
2.4
等比数列
(第二课时)
第一课时
第二课时
学习要点
1. 等比数列的通项公式是怎样的? 它是什么类型的函数?
2. 由通项公式与等比中项能推出等比数列中的哪些项的关系?
3. 怎样用等比数列知识解决某些实际问题?
a2=a1q,
【等比数列的通项公式】
操作题2. 已知等比数列{an}的首项为 a1, 公比为 q,写出这个数列的 a2, a3, a4, a5, 并由此归纳出 an.
a3=a2q
=a1q2,
a4=a3q
=a1q3,
a5=a4q
=a1q4,
……
an=a1qn-1.
等比数列的通项公式:
an=a1qn-1
等比数列 an=a1qn-1 的图象是函数 y = a1qx-1 的图象上 x 取正整数的点.
练习
(补充). 一个等比数列的第 9 项是 公比是 求它的第 1 项;
第 4 题.
(课本53页)
习题 2.4
B组
第 1 题.
解:
由等比数列通项公式得
即
解得 a1=2916,
∴这个数列的第 1 项是 2916.
(补充). 一个等比数列的第 9 项是 公比是 求它的第 1 项;
4. 已知{an}是等比数列.
(1) a52=a3·a7 是否成立? a52=a1·a9 成立吗? 为什么?
(2) an2=an-1·an+1 (n>1) 是否成立? 你据此能得到什么结论?
an2=an-k·an+k (n>k>0) 是否成立? 你又能得到什么结论?
解:
(1)
∵ a52 = (a1q4)2
= a12q8,
a3·a7 = (a1q2)·(a1q6)
= a12q8,
a1·a9 = a1·(a1q8)
= a12q8,
∴ a52 = a3·a7 = a1·a9 成立.
(课本53页)
4. 已知{an}是等比数列.
(1) a52=a3·a7 是否成立? a52=a1·a9 成立吗? 为什么?
(2) an2=an-1·an+1 (n>1) 是否成立? 你据此能得到什么结论?
an2=an-k·an+k (n>k>0) 是否成立? 你又能得到什么结论?
解:
(2)
∵ an2 = (a1qn-1)2
= a12q2n-2,
an-1·an+1 = (a1qn-2)·(a1qn)
= a12q2n-2,
∴ an2 = an-1·an+1 成立.
(课本53页)
4. 已知{an}是等比数列.
(1) a52=a3·a7 是否成立? a52=a1·a9 成立吗? 为什么?
(2) an2=an-1·an+1 (n>1) 是否成立? 你据此能得到什么结论?
an2=an-k·an+k (n>k>0) 是否成立? 你又能得到什么结论?
解:
∵ an2 = (a1qn-1)2
= a12q2n-2,
an-k·an+k = (a1qn-k-1)·(a1qn+k-1)
= a12q2n-2,
∴ an2 = an-k·an+k 成立.
(课本53页)
结论:
an 是 an-k 和 an+k (n>k>0)的等比中项.
在等比数列{an}中,
an2 = an-1·an+1 = an-2·an+2 = an-3·an+3 = …
= an-k·an+k
(1) 如果某项的序号是另外两项序号和的一半, 那么这一项的平方等于另两项的积.
2p=m+n, ? ap2 = am·an.
(2) 如果有两项的序号之和等于另两项的序号之和, 那么这两项的积等于另两项的积.
p+q = m+n, ? ap·aq = am·an.
B 组
1. 已知等比数列{an}的公比为 q, 求证:
证明:
= q(m-1)-(n-1)
= qm-n.
例1. 某种放射性物质不断变化为其他物质, 每经过一年剩留的这种物质是原来的 84%. 这种物质的半衰期为多长 (精确到 1 年)?
解:
经过 n 年后, 这种物质的剩留量是原来的
(84%)n
= 0.84n.
公式可知, 各年剩留量成等比数列, 其中
a1=0.84, q=0.84,
若设原来这种物质的质量为1,
由等比数列通项
要使 an=0.5, 即得
0.84n = 0.5.
两边取常用对数得
nlg0.84 = lg0.5,
≈4.
答: 这种物质的半衰期大约是 4 年.
练习
课本52~53页
第 2、5 题.
2. 在利用电子邮件传播病毒的例子中, 如果第一轮感染的计算机数是80台, 并且从第一轮起, 以后各轮的每一台计算机都可以感染下一轮的20台计算机, 到第 5 轮可以感染多少台计算机?
解:
这是一个首项为80, 公比为20的等比数列模型,
其通项公式为 an= a1qn-1.
则 a5=80?204
=12800000.
答: 到第 5 轮可以感染12800000台计算机.
5. 某人买了一辆价值 13.5万元的新车. 专家预测这种车每年按10%的速度折旧.
(1) 用一个式子表示 n (n?N*)年后这辆车的价值.
(2) 如果他打算用满 4 年时卖掉这辆车, 他大概能得到多少钱?
解:
(1)
每年按10%的速度折旧,
则第 n 年后车子的价值为:
an=13.5(1-10%)n
=13.5?0.9n.
(2)
这人用满 4 年, 车子的价值只有
a4=13.5?0.94
≈8.8574.
答: 这人大概能得到8.8574万元.
【课时小结】
1. 等比数列的通项公式
an=a1qn-1.
通项公式是关于正整数 n 的指数函数类型.
【课时小结】
2. 等比数列中的相等项
an 是 an-k 和 an+k (n>k>0)的等比中项, 即
an2 = an-1·an+1 = an-2·an+2 =…= an-k·an+k.
2p=m+n, ? ap2 = am·an.
p+q = m+n, ? ap·aq = am·an.
或
【课时小结】
3. 等比数列的应用
(1) 判断问题是否可建立等比数列模型;
(2) 建立等比数列模型, 设定相关量;
(3) 用等比数列知识进行相关运算;
(4) 用运算结果解释实际问题.
习题 2.4
A 组
第 1、2、4、5、8 题.
B 组
第 2 题.
解:
1. 在等比数列{an}中,
(1) a4=27, q= -3, 求 a7;
(2) a2=18, a4=8, 求 a1 与 q;
(3) a5=4, a7=6, 求 a9;
(4) a5-a1=15, a4-a2=6, 求 a3.
习题2.4
A 组
(1)
a7=a4q3
=27?(-3)3
= -729.
解:
1. 在等比数列{an}中,
(1) a4=27, q= -3, 求 a7;
(2) a2=18, a4=8, 求 a1 与 q;
(3) a5=4, a7=6, 求 a9;
(4) a5-a1=15, a4-a2=6, 求 a3.
习题2.4
A 组
(2)
得
解方程组得
或
解:
1. 在等比数列{an}中,
(1) a4=27, q= -3, 求 a7;
(2) a2=18, a4=8, 求 a1 与 q;
(3) a5=4, a7=6, 求 a9;
(4) a5-a1=15, a4-a2=6, 求 a3.
习题2.4
A 组
(3)
∵ a7=a5q2,
∴6=4q2,
解得
则 a9=a7q2
= 9.
解:
1. 在等比数列{an}中,
(1) a4=27, q= -3, 求 a7;
(2) a2=18, a4=8, 求 a1 与 q;
(3) a5=4, a7=6, 求 a9;
(4) a5-a1=15, a4-a2=6, 求 a3.
习题2.4
A 组
(4)
由 a5-a1=15, a4-a2=6 得方程组
解方程组得
或
则 a3=1?22=4;
或 a3= -16? = -4.
2. 某地为了保持水土资源, 实行退耕还林, 如果2000年退耕 8 万公顷, 以后每年增加10%, 那么2005年需退耕多少公顷? (结果保留到个位)
解:
在2000年以后的第 n 年退耕数为
an=8(1+10%)n
= 8?1.1n,
2005年即是2000年后的第5年,
即 a5=8?1.15
≈12.8841(万公顷)
=128841公顷.
答: 2005年需退耕128841公顷.
4. 如果能将一张厚度为 0.05 mm 的报纸对折, 再对折, 再对折, …, 对折 50 次后, 报纸的厚度是多少? 你相信这时报纸的厚度可以在地球和月球之间建一座桥吗? (地球与月球之间平均距离约为3.84?105 km)
解:
每次对折后, 厚度是原来的 2 倍,
后的厚度成等比数列, 其公比 q=2,
即每次对折
an=0.1?2n-1,
即 a1=0.1, 则
对折一次后的厚度
为首项,
∴对折50次后的厚度为
a50=0.1?249
≈56294995342131.2 (mm)
≈ 5.63?107 km
这个厚度远远超过了地球与月球之间的平均距离,从理论上讲, 可以在地球与月球之间建一座桥.
(地球到月球的平均距离: 3.8?105 km)
可这座桥有多大呢?
4. 如果能将一张厚度为 0.05 mm 的报纸对折, 再对折, 再对折, …, 对折 50 次后, 报纸的厚度是多少? 你相信这时报纸的厚度可以在地球和月球之间建一座桥吗? (地球与月球之间平均距离约为3.84?105 km)
解:
一张全开报纸按1200?900=1080000(mm2)算,
每对折一次, 面积为原来的二分之一,
则50次对折后的面积为
=1.9?10-9(mm2)
一根粗的头发约为0.002mm2,
0.002?(1.9?10-9)≈1052630.
要一百多万座这样的桥才有一根头发丝大, 谁能走这桥呀!
5. 某城市今年空气质量为 “良” 的天数共为105天,力争 2 年后使空气质量为 “良” 的天数达到240天. 这个城市空气质量为 “良” 的天数的年平均增长率为多少? (精确到小数点后 2 位)
解:
设年均增长率为 q, 今年空气质量为 “良”
的天数为 a1, 则
一年后空气质量为 “良” 的天数为 a2=a1(1+q),
答: 年平均增长率大约是0.51.
2 年后空气质量为 “良” 的天数为 a3=a1(1+q)2.
而 a1=105, a3=240.
即 240=105(1+q)2.
解得 q≈0.51.
8. (1) 在 9 与 243 中间插入两个数, 使它们同这两个数成等比数列;
(2) 在 160 与 5 中间插入 4 个数, 使它们同这两个数成等比数列.
解:
(1)
设这两个数依次为 a, b, 则
a2=9b;
b2=243a,
得 a=27, b=81,
∴这两个数依次为 27, 81.
9, a, b, 243 成等比数列,
a 是 9 与 b 的等比中项, 得
b 是 a 与 243 的等比中项, 得
解这个方程组
8. (1) 在 9 与 243 中间插入两个数, 使它们同这两个数成等比数列;
(2) 在 160 与 5 中间插入 4 个数, 使它们同这两个数成等比数列.
解:
(2)
设所成等比数列为{an}, 则 a1=160, a6=5,
∴有 5=160q5,
解得
∴得
80, 40, 20 和 10.
则插入的 4 个数是
2. 考古学中常利用死亡的生物体中碳14元素稳定持续衰变的现象测定遗址的年代. 假定碳14每年的衰变率不变, 已知它的半衰期为5730年, 那么:
(1) 碳14的衰变率为多少 (精确到0.16)?
(2) 某动物标本中碳14的含量为正常大气中碳14的含量的60% (即衰变了40%), 该动物大约在距今多少年前死亡?
解:
(1)
设衰变率为 x,
(1-x)5730=0.5,
≈0.000121.
答: 碳14的衰变率约为0.0121%.
B 组
2. 考古学中常利用死亡的生物体中碳14元素稳定持续衰变的现象测定遗址的年代. 假定碳14每年的衰变率不变, 已知它的半衰期为5730年, 那么:
(1) 碳14的衰变率为多少 (精确到0.16)?
(2) 某动物标本中碳14的含量为正常大气中碳14的含量的60% (即衰变了40%), 该动物大约在距今多少年前死亡?
解:
(2)
设该动物大约在距今 n 年前死亡.
则 (1-0.000121)n=0.6,
答: 该动物大约在距今4221年前死亡.
0.999879n=0.6,
两边取对数后得
≈4221,
B 组
等比数列
(第一课时)
第一课时
第二课时
操作题1. 请同学们写出下面数列:
(1) 一种细菌进行分裂繁殖, 1 个细菌一次分裂成 2个, 且每分钟分裂一次, 写出 1 个这种细菌经过 1, 2, 3, 4, …, 分钟后的细菌个数;
(2) 一个容器中盛有10升某种溶液, 每次倒出容器中溶液的一半, 写出每次倒出后容器中剩余溶液数量;
(3) 银行的复利计息方式是: 把前一期的利息加入本金计算下一期的利息. 现存入本金10000元, 年利率为1.98%, 写出 5 年内各年末的本利和.
(1) 2, 4, 8, 16, …
(2) 5,
(3) 10000?1.0198, 10000?1.01982,
10000?1.01983, 10000?1.01984, 10000?1.01985.
问题1. 刚才写出的数列是等差数列吗? 如果不是, 那么它们有什么共同的特征? 根据它们的共同特征你想把它们叫做什么数列?
(1) 2, 4, 8, 16, …
(2) 5,
(3) 10000?1.0198, 10000?1.01982,
10000?1.01983, 10000?1.01984, 10000?1.01985.
特征:
各数列中, 每一项与它前一项的比值是一个相等的数.
(1) 中的比值是 2,
(2) 中的比值是
(3) 中的比值是1.0198.
每一项等于前一项乘以 2.
每一项等于前一项乘以
每一项等于前一项乘以 1.0198.
定义: 一般地, 如果一个数列从第 2 项起, 每一项与它的前一项的比等于同一个常数, 那么这个数列就叫做等比数列, 这个常数叫做等比数列的公比,公比通常用字母 q 表示 (q≠0), 即
则数列 {an} 为等比数列, 常数 q 是公比.
判断几个数是否成等比数列, 看其是否满足
判断以通项表示的数列是否是等比数列, 看其是否满足
(常数).
(4) 不是等比数列,
(2) 是等比数列,
(3) 是等比数列,
问题 2. 下列各数列是否是等比数列? 如果是, 公比是多少?
(1) (2)
(3) 7, 7, 7, 7, … (4) 0, 1, 4, 16, …
(1) 是等比数列, 公比 q =
等比数列的任一项都不能为 0.
a2=a1q,
【等比数列的通项公式】
操作题2. 已知等比数列{an}的首项为 a1, 公比为 q,写出这个数列的 a2, a3, a4, a5, 并由此归纳出 an.
a3=a2q
=a1q2,
a4=a3q
=a1q3,
a5=a4q
=a1q4,
……
猜:an=a1qn-1.
等比数列的通项公式:
an=a1qn-1
等比数列 an=a1qn-1 的图象是函数 y = a1qx-1 的图象上 x 取正整数的点.
等比数列的图像
例4. 已知{an}{bn}是项数相同的等比数列, 仿照下表中的例子填写表格. 从中你能得出什么结论? 证明你的结论.
自选 2
自选 1
是
-5?2n-1
例
{an·bn}是否等比数列
an·bn
bn
an
2n
(-3)n
(-6)n
是
-3?(-1)n
是
结论:
如果 {an} {bn} 是项数相同的等比数列, 那么{an·bn} 也是等比数列.
证明如下:
设{an}的公比为 p, {bn}的公比为 q, p, q 为常数,
则
= p·q
(常数),
∴{an·bn}是等比数列.
问题3. 如果{an}是等比数列, c 为常数, 且c≠0,那么{c·an}是否是等比数列, 能证明你的结论吗?
= q (常数).
结论:
一个等比数列的各项都乘以同一个不为 0 的常数,所得的数列仍是等比数列.
问题4. 三个数 2, 3 是否成等比数列? 如果 a, G, b 这三个数成等比数列, G 是多少?
若 a, G, b 成等比数列, 则
? G2=ab,
两比值相等, 三个数成等比数列.
等比中项:
如果在 a 与 b 中间插入一个数 G, 使 a, G, b 成等比数列, 那么 G 叫做 a 与 b 的等比中项,
G2=ab,
等差中项:
如果三个数 a, A, b 成等差数列, 则中间一个数 A 叫做 a 与 b 的等差中项,
或 2A=a+b.
例3. 一个等比数列的第 3 项和第 4 项分别是12和18, 求它的第 1 项与第 2 项.
由等比数列通项公式得,
解:
解关于 a1 与 q 的方程组:
①
②
a3=a1q2=12,
a4=a1q3=18,
②÷① 得
将 q 的值代入①式得
则 a2= a1q
= 8.
∴这个数列的等 1 项是 第 2 项是 8.
练习: (课本53页)
3. 已知{an}是一个无穷等比数列, 公比为 q:
(1) 将{an}中的前 k 项去掉, 剩余各项组成一个新数列, 这个新数列是等比数列吗? 如果是, 它的首项与公比分别是多少?
(2) 取出数列{an}中的所有奇数项, 组成一个新的数列, 这个新数列是等比数列吗? 如果是, 它的首项与公比分别是多少?
(3) 在数列{an}中, 每隔10项取出一项, 组成一个新的数列, 这个新数列是等比数列吗? 如果是, 它的公比是多少? 你能根据得到的结论作出一个猜想吗?
练习: (课本53页)
3. 已知{an}是一个无穷等比数列, 公比为 q:
(1) 将{an}中的前 k 项去掉, 剩余各项组成一个新数列, 这个新数列是等比数列吗? 如果是, 它的首项与公比分别是多少?
答:
其首项是原数列的 ak+1, 公比是原数列的公比 q.
{an} 中去掉前 k 项后分别是
a1+k,
a2+k,
a3+k,
…,
an+k, …
=q,
(常数).
∴{an} 中去掉前 k 项后所得数列是等比数列,
练习: (课本53页)
3. 已知{an}是一个无穷等比数列, 公比为 q:
答:
取出 {an} 中的所有奇数项得
a1, a3, a5, …, a2n-1, …
=q2,
(常数).
∴取出 {an} 中的所有奇数项所得的数列也是等比
数列, 其首项为 a1, 公比为 p2.
(2) 取出数列{an}中的所有奇数项, 组成一个新的数列, 这个新数列是等比数列吗? 如果是, 它的首项与公比分别是多少?
练习: (课本53页)
3. 已知{an}是一个无穷等比数列, 公比为 q:
(3) 在数列{an}中, 每隔10项取出一项, 组成一个新的数列, 这个新数列是等比数列吗? 如果是, 它的公比是多少? 你能根据得到的结论作出一个猜想吗?
答:
在 {an} 中每隔 10 项取出一项得
a11,
=q11,
(常数).
= …
∴ {an} 中每隔 10 项取出一项所得的数列也是等
比数列, 其首项为 a11, 公比为 q11.
a22,
a33,
…,
a10n+n, …
练习: (课本53页)
3. 已知{an}是一个无穷等比数列, 公比为 q:
(3) 在数列{an}中, 每隔10项取出一项, 组成一个新的数列, 这个新数列是等比数列吗? 如果是, 它的公比是多少? 你能根据得到的结论作出一个猜想吗?
猜想:
在等比数列 {an} 中每隔 k 项取出一项,
所得的数列也是等比数列, 其首项为 ak+1, 公比为
qk+1.
【课时小结】
1. 等比数列
一个数列从第 2 项起的每一项与它前一项的比等于同一个常数 q, 则这个数列就叫做等比数列, 常数 q 叫做等比数列的公比, 即
a2=a1·q, a3=a2·q, a4=a3·q, ……, an+1=an·q.
是判定等比数列的条件.
【课时小结】
2. 等比中项
如果在 a 与 b 中间插入一个数 G, 使 a, G, b 成等比数列, 那么 G 叫做 a 与 b 的等比中项, 即
G2=ab.
习题 2.4
A 组
第 3、6、7 题.
习题 2.4
A 组
3. 已知{an}是各项均为正数的等比数列, 是等比数列吗? 为什么?
解:
(常数),
∴ 是等比数列.
6. 已知 a, b 是互异的正数, A 是 a, b 的等差中项, G 是 a, b 的等比中项, A 与 G 有无确定的大小关系?
解:
由题设得
∵a>0, b>0, a≠b,
∴一定有 A>G.
即
得
7. 求下列各组数的等比中项:
(1)
(2) a4+a2b2 与 b4+a2b2 (a≠0, b≠0).
解:
(1)
=±2.
(2)
=±ab(a2+b2).
2.4
等比数列
(第二课时)
第一课时
第二课时
学习要点
1. 等比数列的通项公式是怎样的? 它是什么类型的函数?
2. 由通项公式与等比中项能推出等比数列中的哪些项的关系?
3. 怎样用等比数列知识解决某些实际问题?
a2=a1q,
【等比数列的通项公式】
操作题2. 已知等比数列{an}的首项为 a1, 公比为 q,写出这个数列的 a2, a3, a4, a5, 并由此归纳出 an.
a3=a2q
=a1q2,
a4=a3q
=a1q3,
a5=a4q
=a1q4,
……
an=a1qn-1.
等比数列的通项公式:
an=a1qn-1
等比数列 an=a1qn-1 的图象是函数 y = a1qx-1 的图象上 x 取正整数的点.
练习
(补充). 一个等比数列的第 9 项是 公比是 求它的第 1 项;
第 4 题.
(课本53页)
习题 2.4
B组
第 1 题.
解:
由等比数列通项公式得
即
解得 a1=2916,
∴这个数列的第 1 项是 2916.
(补充). 一个等比数列的第 9 项是 公比是 求它的第 1 项;
4. 已知{an}是等比数列.
(1) a52=a3·a7 是否成立? a52=a1·a9 成立吗? 为什么?
(2) an2=an-1·an+1 (n>1) 是否成立? 你据此能得到什么结论?
an2=an-k·an+k (n>k>0) 是否成立? 你又能得到什么结论?
解:
(1)
∵ a52 = (a1q4)2
= a12q8,
a3·a7 = (a1q2)·(a1q6)
= a12q8,
a1·a9 = a1·(a1q8)
= a12q8,
∴ a52 = a3·a7 = a1·a9 成立.
(课本53页)
4. 已知{an}是等比数列.
(1) a52=a3·a7 是否成立? a52=a1·a9 成立吗? 为什么?
(2) an2=an-1·an+1 (n>1) 是否成立? 你据此能得到什么结论?
an2=an-k·an+k (n>k>0) 是否成立? 你又能得到什么结论?
解:
(2)
∵ an2 = (a1qn-1)2
= a12q2n-2,
an-1·an+1 = (a1qn-2)·(a1qn)
= a12q2n-2,
∴ an2 = an-1·an+1 成立.
(课本53页)
4. 已知{an}是等比数列.
(1) a52=a3·a7 是否成立? a52=a1·a9 成立吗? 为什么?
(2) an2=an-1·an+1 (n>1) 是否成立? 你据此能得到什么结论?
an2=an-k·an+k (n>k>0) 是否成立? 你又能得到什么结论?
解:
∵ an2 = (a1qn-1)2
= a12q2n-2,
an-k·an+k = (a1qn-k-1)·(a1qn+k-1)
= a12q2n-2,
∴ an2 = an-k·an+k 成立.
(课本53页)
结论:
an 是 an-k 和 an+k (n>k>0)的等比中项.
在等比数列{an}中,
an2 = an-1·an+1 = an-2·an+2 = an-3·an+3 = …
= an-k·an+k
(1) 如果某项的序号是另外两项序号和的一半, 那么这一项的平方等于另两项的积.
2p=m+n, ? ap2 = am·an.
(2) 如果有两项的序号之和等于另两项的序号之和, 那么这两项的积等于另两项的积.
p+q = m+n, ? ap·aq = am·an.
B 组
1. 已知等比数列{an}的公比为 q, 求证:
证明:
= q(m-1)-(n-1)
= qm-n.
例1. 某种放射性物质不断变化为其他物质, 每经过一年剩留的这种物质是原来的 84%. 这种物质的半衰期为多长 (精确到 1 年)?
解:
经过 n 年后, 这种物质的剩留量是原来的
(84%)n
= 0.84n.
公式可知, 各年剩留量成等比数列, 其中
a1=0.84, q=0.84,
若设原来这种物质的质量为1,
由等比数列通项
要使 an=0.5, 即得
0.84n = 0.5.
两边取常用对数得
nlg0.84 = lg0.5,
≈4.
答: 这种物质的半衰期大约是 4 年.
练习
课本52~53页
第 2、5 题.
2. 在利用电子邮件传播病毒的例子中, 如果第一轮感染的计算机数是80台, 并且从第一轮起, 以后各轮的每一台计算机都可以感染下一轮的20台计算机, 到第 5 轮可以感染多少台计算机?
解:
这是一个首项为80, 公比为20的等比数列模型,
其通项公式为 an= a1qn-1.
则 a5=80?204
=12800000.
答: 到第 5 轮可以感染12800000台计算机.
5. 某人买了一辆价值 13.5万元的新车. 专家预测这种车每年按10%的速度折旧.
(1) 用一个式子表示 n (n?N*)年后这辆车的价值.
(2) 如果他打算用满 4 年时卖掉这辆车, 他大概能得到多少钱?
解:
(1)
每年按10%的速度折旧,
则第 n 年后车子的价值为:
an=13.5(1-10%)n
=13.5?0.9n.
(2)
这人用满 4 年, 车子的价值只有
a4=13.5?0.94
≈8.8574.
答: 这人大概能得到8.8574万元.
【课时小结】
1. 等比数列的通项公式
an=a1qn-1.
通项公式是关于正整数 n 的指数函数类型.
【课时小结】
2. 等比数列中的相等项
an 是 an-k 和 an+k (n>k>0)的等比中项, 即
an2 = an-1·an+1 = an-2·an+2 =…= an-k·an+k.
2p=m+n, ? ap2 = am·an.
p+q = m+n, ? ap·aq = am·an.
或
【课时小结】
3. 等比数列的应用
(1) 判断问题是否可建立等比数列模型;
(2) 建立等比数列模型, 设定相关量;
(3) 用等比数列知识进行相关运算;
(4) 用运算结果解释实际问题.
习题 2.4
A 组
第 1、2、4、5、8 题.
B 组
第 2 题.
解:
1. 在等比数列{an}中,
(1) a4=27, q= -3, 求 a7;
(2) a2=18, a4=8, 求 a1 与 q;
(3) a5=4, a7=6, 求 a9;
(4) a5-a1=15, a4-a2=6, 求 a3.
习题2.4
A 组
(1)
a7=a4q3
=27?(-3)3
= -729.
解:
1. 在等比数列{an}中,
(1) a4=27, q= -3, 求 a7;
(2) a2=18, a4=8, 求 a1 与 q;
(3) a5=4, a7=6, 求 a9;
(4) a5-a1=15, a4-a2=6, 求 a3.
习题2.4
A 组
(2)
得
解方程组得
或
解:
1. 在等比数列{an}中,
(1) a4=27, q= -3, 求 a7;
(2) a2=18, a4=8, 求 a1 与 q;
(3) a5=4, a7=6, 求 a9;
(4) a5-a1=15, a4-a2=6, 求 a3.
习题2.4
A 组
(3)
∵ a7=a5q2,
∴6=4q2,
解得
则 a9=a7q2
= 9.
解:
1. 在等比数列{an}中,
(1) a4=27, q= -3, 求 a7;
(2) a2=18, a4=8, 求 a1 与 q;
(3) a5=4, a7=6, 求 a9;
(4) a5-a1=15, a4-a2=6, 求 a3.
习题2.4
A 组
(4)
由 a5-a1=15, a4-a2=6 得方程组
解方程组得
或
则 a3=1?22=4;
或 a3= -16? = -4.
2. 某地为了保持水土资源, 实行退耕还林, 如果2000年退耕 8 万公顷, 以后每年增加10%, 那么2005年需退耕多少公顷? (结果保留到个位)
解:
在2000年以后的第 n 年退耕数为
an=8(1+10%)n
= 8?1.1n,
2005年即是2000年后的第5年,
即 a5=8?1.15
≈12.8841(万公顷)
=128841公顷.
答: 2005年需退耕128841公顷.
4. 如果能将一张厚度为 0.05 mm 的报纸对折, 再对折, 再对折, …, 对折 50 次后, 报纸的厚度是多少? 你相信这时报纸的厚度可以在地球和月球之间建一座桥吗? (地球与月球之间平均距离约为3.84?105 km)
解:
每次对折后, 厚度是原来的 2 倍,
后的厚度成等比数列, 其公比 q=2,
即每次对折
an=0.1?2n-1,
即 a1=0.1, 则
对折一次后的厚度
为首项,
∴对折50次后的厚度为
a50=0.1?249
≈56294995342131.2 (mm)
≈ 5.63?107 km
这个厚度远远超过了地球与月球之间的平均距离,从理论上讲, 可以在地球与月球之间建一座桥.
(地球到月球的平均距离: 3.8?105 km)
可这座桥有多大呢?
4. 如果能将一张厚度为 0.05 mm 的报纸对折, 再对折, 再对折, …, 对折 50 次后, 报纸的厚度是多少? 你相信这时报纸的厚度可以在地球和月球之间建一座桥吗? (地球与月球之间平均距离约为3.84?105 km)
解:
一张全开报纸按1200?900=1080000(mm2)算,
每对折一次, 面积为原来的二分之一,
则50次对折后的面积为
=1.9?10-9(mm2)
一根粗的头发约为0.002mm2,
0.002?(1.9?10-9)≈1052630.
要一百多万座这样的桥才有一根头发丝大, 谁能走这桥呀!
5. 某城市今年空气质量为 “良” 的天数共为105天,力争 2 年后使空气质量为 “良” 的天数达到240天. 这个城市空气质量为 “良” 的天数的年平均增长率为多少? (精确到小数点后 2 位)
解:
设年均增长率为 q, 今年空气质量为 “良”
的天数为 a1, 则
一年后空气质量为 “良” 的天数为 a2=a1(1+q),
答: 年平均增长率大约是0.51.
2 年后空气质量为 “良” 的天数为 a3=a1(1+q)2.
而 a1=105, a3=240.
即 240=105(1+q)2.
解得 q≈0.51.
8. (1) 在 9 与 243 中间插入两个数, 使它们同这两个数成等比数列;
(2) 在 160 与 5 中间插入 4 个数, 使它们同这两个数成等比数列.
解:
(1)
设这两个数依次为 a, b, 则
a2=9b;
b2=243a,
得 a=27, b=81,
∴这两个数依次为 27, 81.
9, a, b, 243 成等比数列,
a 是 9 与 b 的等比中项, 得
b 是 a 与 243 的等比中项, 得
解这个方程组
8. (1) 在 9 与 243 中间插入两个数, 使它们同这两个数成等比数列;
(2) 在 160 与 5 中间插入 4 个数, 使它们同这两个数成等比数列.
解:
(2)
设所成等比数列为{an}, 则 a1=160, a6=5,
∴有 5=160q5,
解得
∴得
80, 40, 20 和 10.
则插入的 4 个数是
2. 考古学中常利用死亡的生物体中碳14元素稳定持续衰变的现象测定遗址的年代. 假定碳14每年的衰变率不变, 已知它的半衰期为5730年, 那么:
(1) 碳14的衰变率为多少 (精确到0.16)?
(2) 某动物标本中碳14的含量为正常大气中碳14的含量的60% (即衰变了40%), 该动物大约在距今多少年前死亡?
解:
(1)
设衰变率为 x,
(1-x)5730=0.5,
≈0.000121.
答: 碳14的衰变率约为0.0121%.
B 组
2. 考古学中常利用死亡的生物体中碳14元素稳定持续衰变的现象测定遗址的年代. 假定碳14每年的衰变率不变, 已知它的半衰期为5730年, 那么:
(1) 碳14的衰变率为多少 (精确到0.16)?
(2) 某动物标本中碳14的含量为正常大气中碳14的含量的60% (即衰变了40%), 该动物大约在距今多少年前死亡?
解:
(2)
设该动物大约在距今 n 年前死亡.
则 (1-0.000121)n=0.6,
答: 该动物大约在距今4221年前死亡.
0.999879n=0.6,
两边取对数后得
≈4221,
B 组
